基于导弹三通道耦合模型的控制参数设计

邱亚男, 梁晓庚,, 贾晓洪

(西北工业大学 自动化学院, 陕西 西安 710072;2.中国空空导弹研究院 航空制导武器航空科技重点实验室, 河南 洛阳 471009)



基于导弹三通道耦合模型的控制参数设计

邱亚男1, 梁晓庚1,2, 贾晓洪2

(西北工业大学 自动化学院, 陕西 西安 710072;2.中国空空导弹研究院 航空制导武器航空科技重点实验室, 河南 洛阳 471009)

摘要:针对导弹自动驾驶仪控制参数设计问题及耦合对控制系统设计的影响,提出了一种基于PSO算法的三通道耦合状态空间控制参数设计方法。建立了自动驾驶仪三通道全状态耦合线性化模型,通过对线性化模型的建立、控制系统性能指标的选取、PSO算法的参数设置及适应度函数的编写,实现了基于PSO算法对自动驾驶仪控制参数的自动设计。仿真结果表明,该方法设计的控制参数优于三通道解耦独立设计的控制参数,设计结果具有良好的动态品质和鲁棒性,并具有较快的收敛速度和良好的全局搜索能力,是一种有效的控制参数自动设计方法。

关键词:PSO算法; 三通道耦合; 自动驾驶仪; 参数优化

0引言

导弹在小迎角飞行时,通道耦合和气动非线性可以忽略,可近似地认为系统是完全解耦的线性系统。随着对导弹性能要求的提高,导弹攻击大机动目标需要作大迎角飞行时,其扰动以及控制面上的不确定效应等诸多因素都会造成导弹气动特性严重的非线性、耦合以及不确定性等,这就要求控制系统不但具有较好的动态性能,而且还必须具备一定的鲁棒性。但是,控制系统的快速性和稳定性是相互制约、相互影响的,这就增大了稳定和控制综合设计的困难[1-4]。基于单通道模型独立设计的控制参数,对具有很强耦合特性的非线性系统是否能够及时抑制干扰力矩的影响,并保持控制回路的稳定性和鲁棒性,有待进一步进行分析和验证。

粒子群算法[5-7](Particle Swarm Optimization,PSO)是进化算法的一种,源于对鸟群捕食行为的研究。粒子群算法本质上属于一种迭代的随机搜索算法,具有并行处理特征,且鲁棒性好,可以较大概率地找到优化问题的全局最优解。由于该算法概念清晰,易于实现,计算效率高,目前已成功应用于求解各种复杂的优化问题[8-10]。

本文针对导弹多输入多输出强耦合系统的特性,提出PSO算法控制参数自动优化的改进措施,即在三通道耦合状态下直接设计控制参数,使控制系统具有更真实的相对稳定性和鲁棒性。导弹飞行特性对于飞行包线内不同特征点的要求不同,相应地对自动驾驶仪快速性和稳定性的要求不同。因此在不同的特征点进行控制参数设计时,适应度函数根据控制系统对快速性和稳定性的要求,包含了系统时域和频域指标性能的惩罚函数,并通过对各项指标进行相应的适当加权,可得到满足不同性能要求的最优参数或次优参数,从而使得自动驾驶仪的综合性能达到最优。该方法直接根据控制系统耦合状态响应对控制器参数进行整定,设计的控制参数能够满足自动驾驶仪性能指标要求,且可以消除或抑制扰动和交叉耦合的影响,最终达到自动驾驶仪稳定精确地跟踪制导指令的目的。

1导弹动力学模型

导弹本身是一个时变的、非线性的弹性结构体,其数学模型非常复杂,因而不便于控制系统设计。为了使设计工作简便可靠,必须对其数学模型进行简化。弹体全状态耦合模型如下:

(1)

其矩阵形式为:

(2)

(3)

三通道耦合模型考虑了导弹的通道间耦合,更真实地反映了弹体的气动特性和动态运动过程。运用上述弹体全状态耦合状态方程,与舵机、传感器和三通道自动驾驶仪闭合,即可建立三通道耦合自动驾驶仪模型[11-12]。在Simulink环境下建立的三通道耦合自动驾驶仪模型如图1所示。

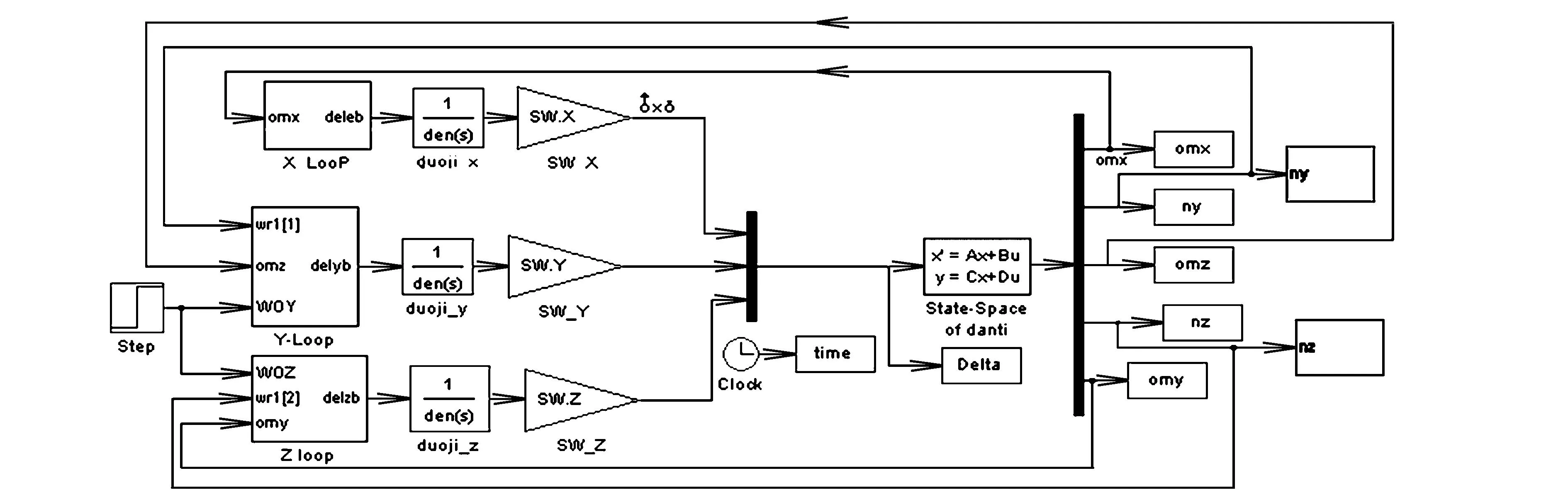
图1　三通道耦合自动驾驶仪模型Fig.1　Three-channel coupling autopilot model

2控制参数优化设计

本文确立采用PSO算法的惯性权重模型来实现三通道耦合模型自动驾驶仪的控制参数自动设计,遵循适应性原则、可靠性原则、收敛性原则、稳定性原则和生物类比原则,开展可行性的设计方案,具体步骤如下:

(1)确定自动驾驶仪结构模型及设计对象;

(2)建立自动驾驶仪与PSO算法的接口模型;

(3)设置PSO优化算法的参数;

(4)选择优化性能评价标准,即编写适应度函数;

(5)采用PSO算法进行控制参数设计,并进行特征点设计;

(6)通过对诸多特征点的调试,修正PSO算法的参数设置及适应度函数,使之对不同的空域都能搜索到较好的控制参数;

(7)对全空域控制算法进行设计,并进行仿真验证;

(8)在仿真基础上对PSO算法进行优化,形成自动驾驶仪控制参数自动设计软件。

根据上述设计步骤,最终确立的设计流程如图2所示。

图2　自动设计流程Fig.2　Automatic design flow chart

在三通道耦合线性化模型基础上设计控制参数,主要完成粒子群的初始化及适应度函数的修正:

(1)粒子的长度和范围。对于三通道耦合模型下的自动驾驶仪,需要设计11个控制参数,粒子的长度为11,粒子的范围由参数的取值范围来确定。

(2)适应度函数的修正。在PSO算法中,参数自动设计的优劣很大程度上取决于适应度函数的合理与否,一个好的适应度函数是寻优成功的必备条件,是影响优化算法质量的一个关键因素,也直接关系到参数整定的结果以及系统的控制品质。

适应度函数一般需要确定一些性能指标。反映参数设计效果的性能指标必须能综合反映系统的控制质量,且便于分析计算。具体进行参数设计时,根据需要选择不同的性能指标。在进行自动驾驶仪控制参数自动设计时,适应度函数考虑了系统的稳定性、时域特性及参数量级统一的问题,具体如图3所示。

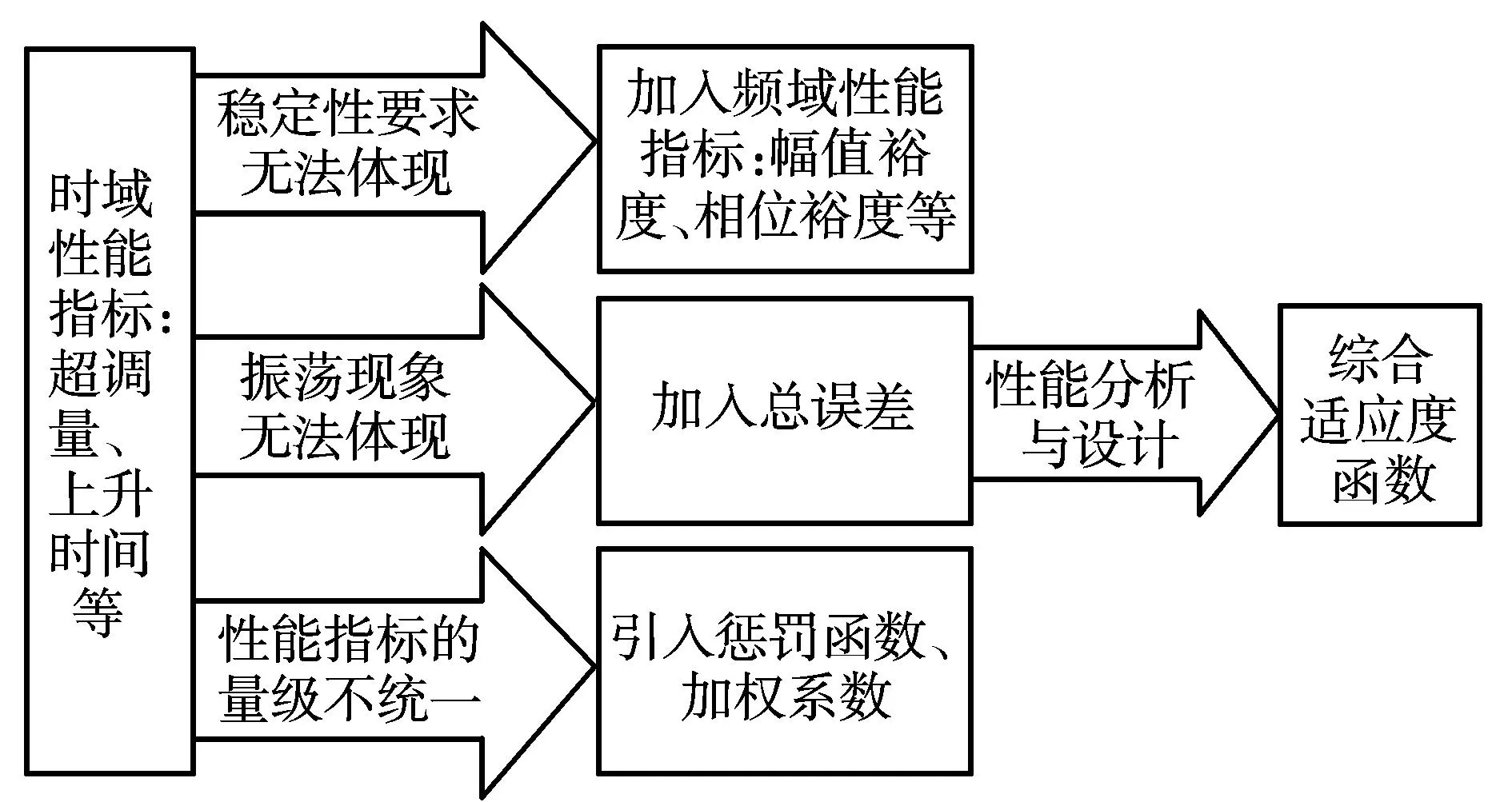
图3　适应度函数编写Fig.3　Design of the fitness function

本文在包含超调量、上升时间和稳态误差等时域指标项以及幅值裕度和相位裕度等频域指标项基础上,在三通道控制参数设计中加入了穿越频率指标项,并对考核指标项进行了修正:

(4)

3设计结果与六自由度仿真

如表1所示,选择不同高度、不同马赫数和不同飞行迎角的3个特征点进行控制参数自动设计。表2给出了设计点所得到的设计性能指标,包含上升时间、超调量、稳态误差、幅值裕度(G)和相位裕度(Φ)等。

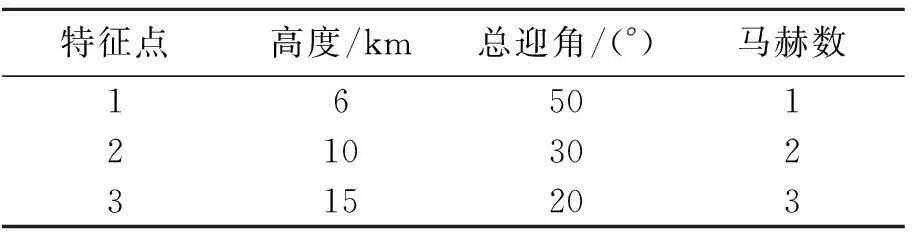
表1　寻优特征点

表2　所选特征点的设计性能指标

从表2可以看出,通过对不同高度、不同飞行迎角等多个状态下特征点的设计,均取得了较为理想的效果。特征点1的三通道耦合模型下的仿真结果如图4～图9所示。

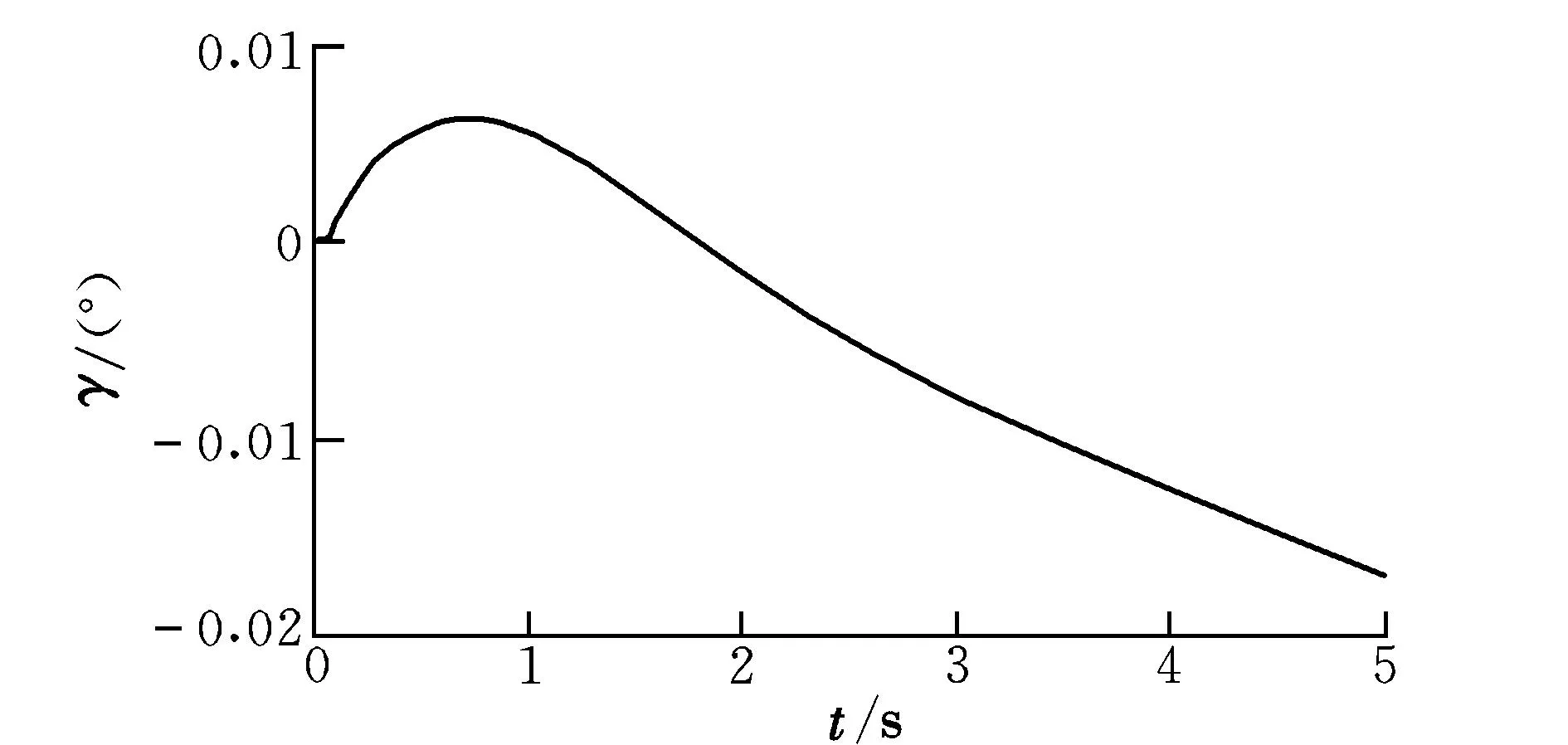
图4　滚转角响应Fig.4　Roll angel response

图5　俯仰通道过载响应Fig.5　Dynamic response of pitch channel

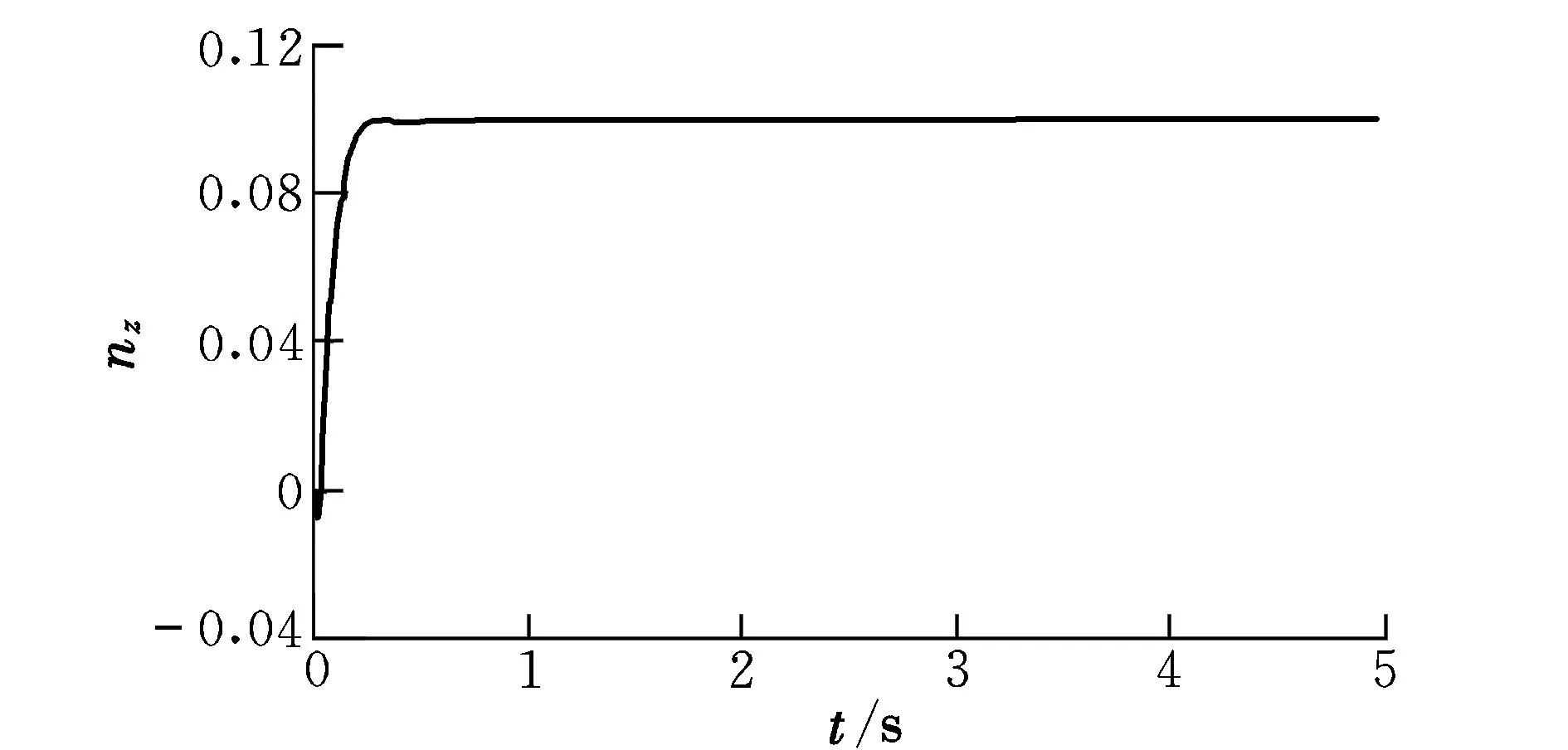
图6　偏航通道过载响应Fig.6　Dynamic response of yaw channel

由图5和图6的过载响应曲线可以看出:上升时间tr<0.3 s;超调量σ<3%;稳态误差Err<2%。

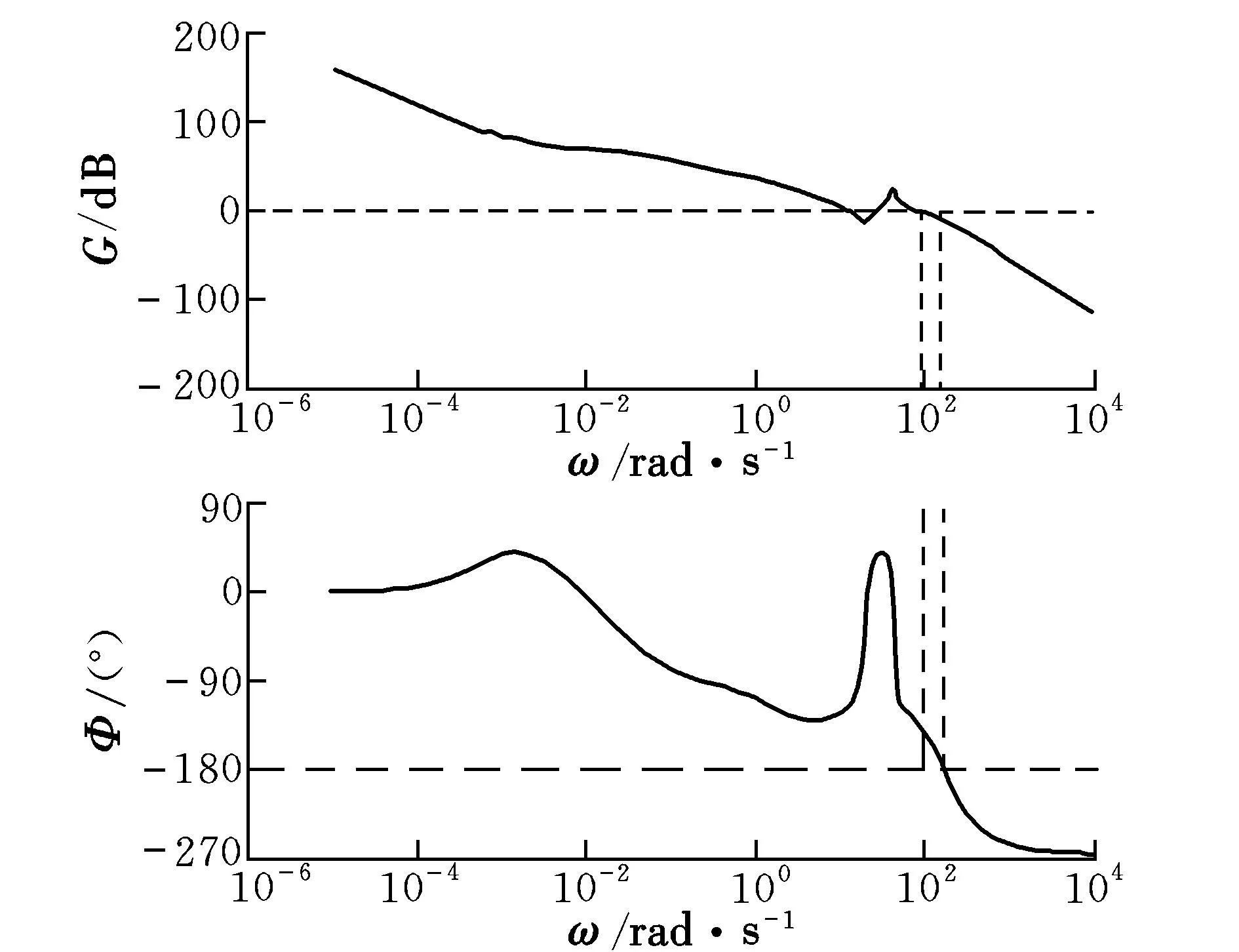
图7　滚转通道开环频率特性Fig.7　Open-loop frequency characteristic of roll channel

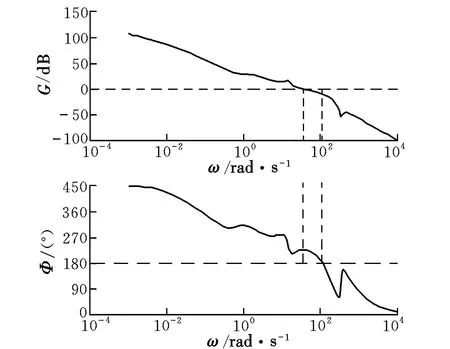
图8　俯仰通道开环频域特性Fig.8　Open-loop frequency characteristic of pitch channel

图9　偏航通道开环频域特性Fig.9　Open-loop frequency characteristic of yaw channel

由图7～图9可以看出:幅值裕度满足G>6 dB;相位裕度满足Φ>30°。对于三通道设计的特征点,在满足系统对于自动驾驶仪设计要求的同时,也保证了自动驾驶仪的空间稳定性。把该点在单通道的设计结果与三通道耦合状态下的响应特性和稳定特性进行对比分析可知,在设计结果的动态品质得到提高的同时,空间稳定裕度也得到了改善。

4结束语

本文针对耦合对控制系统设计的影响,提出了一种基于PSO算法的三通道耦合状态空间控制参数设计方法,该方法可以兼顾多项性能指标。六自由度仿真结果表明,该方法设计的控制参数优于三通道解耦独立设计的控制参数[13],设计结果具有良好的动态品质和鲁棒性,具有较快的收敛速度和良好的全局搜索能力,是一种有效的控制参数自动设计方法。三通道耦合状态设计不同于传统意义上的自动驾驶仪控制参数设计,该方法的可行性为自动驾驶仪控制参数的设计提出了新的思路。

参考文献：

[1]程云龙.防空导弹自动驾驶仪设计[M].北京:宇航出版社,1993.

[2]刘智平,周凤歧,周军.战术导弹现代自动驾驶仪设计方法综述[J].航天控制,2006,24(10):91-96.

[3]李友年,贾晓洪,王海波.H∞控制理论在空空导弹自动驾驶仪设计中的应用[J].航空兵器,2006(6):12-14.

[4]雷延花,陈士橹.导弹气动耦合分析与解耦算法研究[J].弹道学报,2003,15 (1):11-15.

[5]Kennedy J,Eberhart R C.Particle swarm optimization[C]//Proceedings IEEE International Conference Neural

Networks IV. Piscataway NJ:IEEE Service Center,1995:1942-1948.

[6]Eberhart R C,Kennedy J.A new optimizer using particle swarm theory [C]//Proceedings the 6th International Symposium on Micro Machine and Human Science.Nagoya,1995:39-43.

[7]Shi Y H,Eberhart R C.Parameter selection in particle swarm optimization[C]//1998 Annual Conference on Evolutionary Programming.San Diego,1998:591-600.

[8]孙逊,章卫国,尹伟,等.基于粒子群优化算法的模糊飞行控制器设计[J].弹箭与制导学报,2007,26(2):132-133.

[9]李广文,章卫国,李建,等.基于均匀设计的粒子群算法及其在飞控系统中的应用[J].计算机应用,2007(3):727-729.

[10]胡峪,周兆英.粒子群优化算法在微型无人机设计中的应用[J].飞行力学,2004,22(2):61-64.

[11]杨华东,张友安,苏身榜.基于Matlab/Simulink的空空导弹全弹道六自由度数学仿真建模[J].战术导弹控制技术,2002(4):1-8.

[12]Mracek C P,Ridgely D B.Missile longitudinal autopilots:comparison of multiple three loop topologies[R].AIAA-2005-6380,2005.

[13]邱亚男,王建琦,贾晓洪.基于PSO算法的自动驾驶仪控制参数设计[J].航天控制,2009,27(6):28-32.

(编辑：崔立峰)

Control parameter optimization based on a three-channel coupling autopilot

QIU Ya-nan1, LIANG Xiao-geng1,2, JIA Xiao-hong2

(1.School of Automation, Northwestern Polytechnical University, Xi’an 710072, China;2.Key Laboratory of Aviation Science for Airborne Guided Weapons,CAMA, Luoyang 471009, China)

Abstract:In this paper, a parameter tuning method based on particle swarm optimization (PSO) algorithm is proposed, which was applied to optimize control parameters of a three-channel coupling autopilot. First, a three-channel coupling model is built. Then the parameter of PSO algorithm is set up and a fitness function of PSO algorithm is defined. The PSO algorithm is used in the optimization of autopilot controller such that automatic tuning of the autopilot controlling parameters can be achieved. Simulation results show that the proposed method is more effective than the method based on single-channel autopilot and has achieved robust dynamic performance. In addition, the proposed method has a faster convergence speed and a better global searching capability, which could save time and reduce the cost. So it can be concluded that the method is effective in automatic design of parameters.

Key words:PSO algorithm; three-channel coupling; autopilot; parameter optimization

中图分类号：TJ765.3

文献标识码：A

文章编号：1002-0853(2016)01-0063-05

作者简介:邱亚男(1986-)，女，河南洛宁人，博士研究生，研究方向为飞行器制导与控制。

基金项目:航空科学基金资助(20100196002)

收稿日期:2015-05-14;

修订日期:2015-09-06; 网络出版时间:2015-09-22 15:36