前后掠翼鸭式布局中鸭翼涡的流动机理

张冬, 胡孟权, 王旭, 吴章沅

(空军工程大学 航空航天工程学院, 陕西 西安 710038)



前后掠翼鸭式布局中鸭翼涡的流动机理

张冬, 胡孟权, 王旭, 吴章沅

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

摘要:基于前后掠鸭式布局的简化模型,通过求解雷诺平均N-S方程,模拟了前后掠鸭式布局的绕流结构,得到了不同布局下鸭翼的升力系数曲线。通过空间流线图,分析了单独鸭翼漩涡的发展特点,以及不同布局中鸭翼涡与机翼前缘涡的干扰机理。结果表明:在后掠翼鸭式布局中,鸭翼涡在大迎角时受到机翼前缘涡的有利干扰,增大了鸭翼的升力系数,提高了失速迎角;在前掠翼鸭式布局中,鸭翼的最大升力系数有所提高,失速迎角基本保持不变。

关键词:鸭式布局; 鸭翼涡; 流动机理

0引言

近距耦合鸭式布局涡系之间可以产生有利干扰,提高布局的升力系数和失速迎角[1-4]。现代战斗机追求机动性和敏捷性,尤其是大迎角和过失速机动能力,近距耦合鸭式布局是现代战斗机经常采用的先进布局之一。

瑞典的Behrbohm[5]在20世纪60年代中期研究发现, 近距耦合鸭式布局的鸭翼涡可对机翼前缘涡产生有利干扰, 从而增加布局的升力系数, 并提高布局的失速迎角,SAAB-37飞机的设计就成功运用了该研究成果。此后,许多战斗机采用近距耦合鸭式布局,如瑞典的JAS-39、法国的幻影和阵风等,都属于后掠翼鸭式布局;美国的X-29和俄罗斯的Su-47则是前掠翼鸭式布局中的典型代表。

在近距耦合鸭式布局中,鸭翼兼有气动增升部件及操纵面双重功能[6],鸭翼的气动特性对主机翼以及整机的性能有着十分重要的影响。对气动布局中的鸭翼气动特性进行深入分析,有助于充分利用鸭翼带来的气动收益。在前后掠翼鸭式布局中,由于机翼的流动存在不同的特点,鸭翼涡受到机翼前缘涡的干扰也有所不同,对这两种布局下鸭翼涡流动机理的研究是十分必要的。对于复杂涡系的干扰分析,实验研究有很大的难度,而数值仿真及其后处理则有着独特的优势,本文通过数值计算,研究了前后掠鸭式布局中鸭翼涡的发展过程,分析了机翼前缘涡对鸭翼涡的干扰作用。

1计算模型和网格

由于本文主要研究鸭翼涡的流动机理以及机翼对鸭翼流动的干扰,为方便分析,计算采用平板模型(C代表单独鸭翼,BC代表后掠翼鸭式布局, BSC代表带边条的后掠翼鸭式布局, FC代表前掠翼鸭式布局,FSC代表带边条的前掠翼鸭式布局),模型厚度4 mm,迎风面边缘皆倒角45°,从而在小迎角下就能产生稳定的漩涡。鸭翼与机翼共面,鸭翼前缘后掠角56°,后缘后掠角25°,鸭翼翼根弦长4 mm,翼尖弦长24 mm,展长100 mm。保持前后掠机翼的翼面积、展弦比、根梢比和1/4弦线后掠角相同,边条后掠70°,图1为不同鸭翼布局的平面示意图。

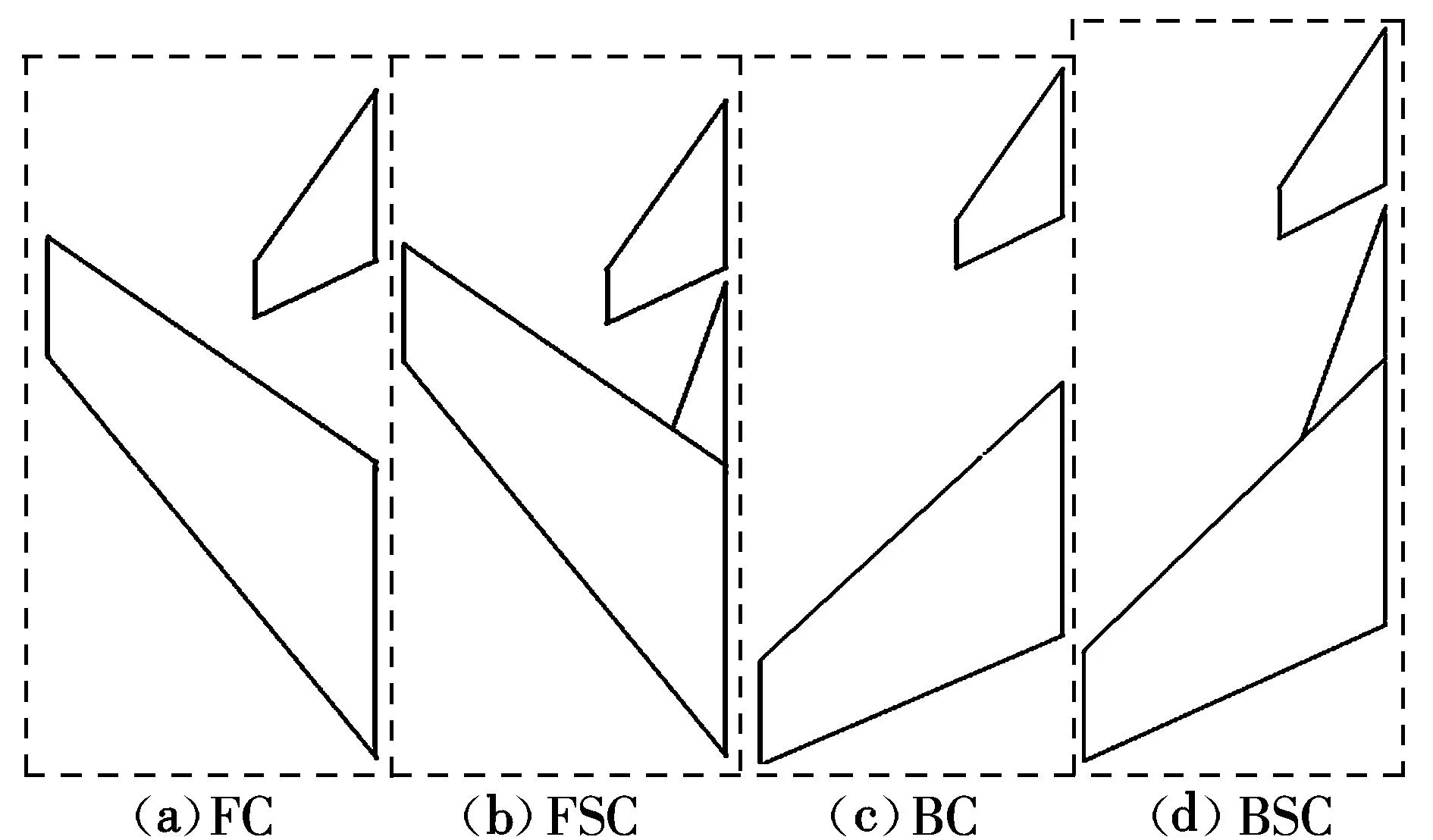
图1　不同鸭翼布局平面示意图Fig.1　Diagram of different canard configurations

由于模型的几何对称性,本文在计算时采用半模,并采用结构网格,图2为BSC和FSC布局的网格分布。网格划分时,边界层内第1层网格高度控制为机翼平均气动弦长的10-6,y+值在0～1之间,以满足飞机表面粘性边界层的计算要求[7],从而保证能够模拟边界层内的流动特征。各模型网格数量控制在1.5×106～3.0×106。

图2　BSC和FSC布局网格分布Fig.2　Surface mesh of BSC and FSC configuration

2计算方法

数值模拟的控制方程采用三维Navier-Stokes方程。在直角坐标系中,无热源的三维Navier-Stokes方程守恒形式为[8]:

式中:w为状态矢量;f为无粘(对流)通矢量项;fv为粘性(耗散)通矢量项。

湍流模型选用SST (Shear-Stress Transport)k-ω模型,考虑了低雷诺数和剪切流,加入了横向耗散导数项,并在定义湍流粘度时考虑了湍流剪切应力的输运过程,适合有逆压梯度的流动计算[9]。

采用有限体积法对控制方程进行离散,对流项选用二阶迎风差分格式[10]。远场条件为压力远场,对称面为对称边界条件,物面为无滑移壁面条件,计算残差收敛精度为10-5。

3计算结果及分析

3.1不同鸭翼的升力系数

图3给出了不同布局下鸭翼气动升力系数的计算结果。可以看出:后掠翼鸭式布局能大幅提高鸭翼最大升力系数,并延迟失速,尤其是带边条后掠翼鸭式布局,不仅能大幅提高最大升力系数,还能使失速后鸭翼的升力系数下降变得平缓,极大地改善了鸭翼的失速特性,这是因为大迎角下鸭翼涡与机翼前缘涡之间存在着有利干扰;对于前掠翼鸭式布局,鸭翼的最大升力系数有少量提高,失速迎角基本不变,失速后升力系数下降缓慢;在带边条的后掠翼鸭式布局中,鸭翼的最大升力系数和失速迎角都有明显提高,这说明在大迎角下,鸭翼涡、边条涡和机翼前缘涡之间的有利干扰更加明显。

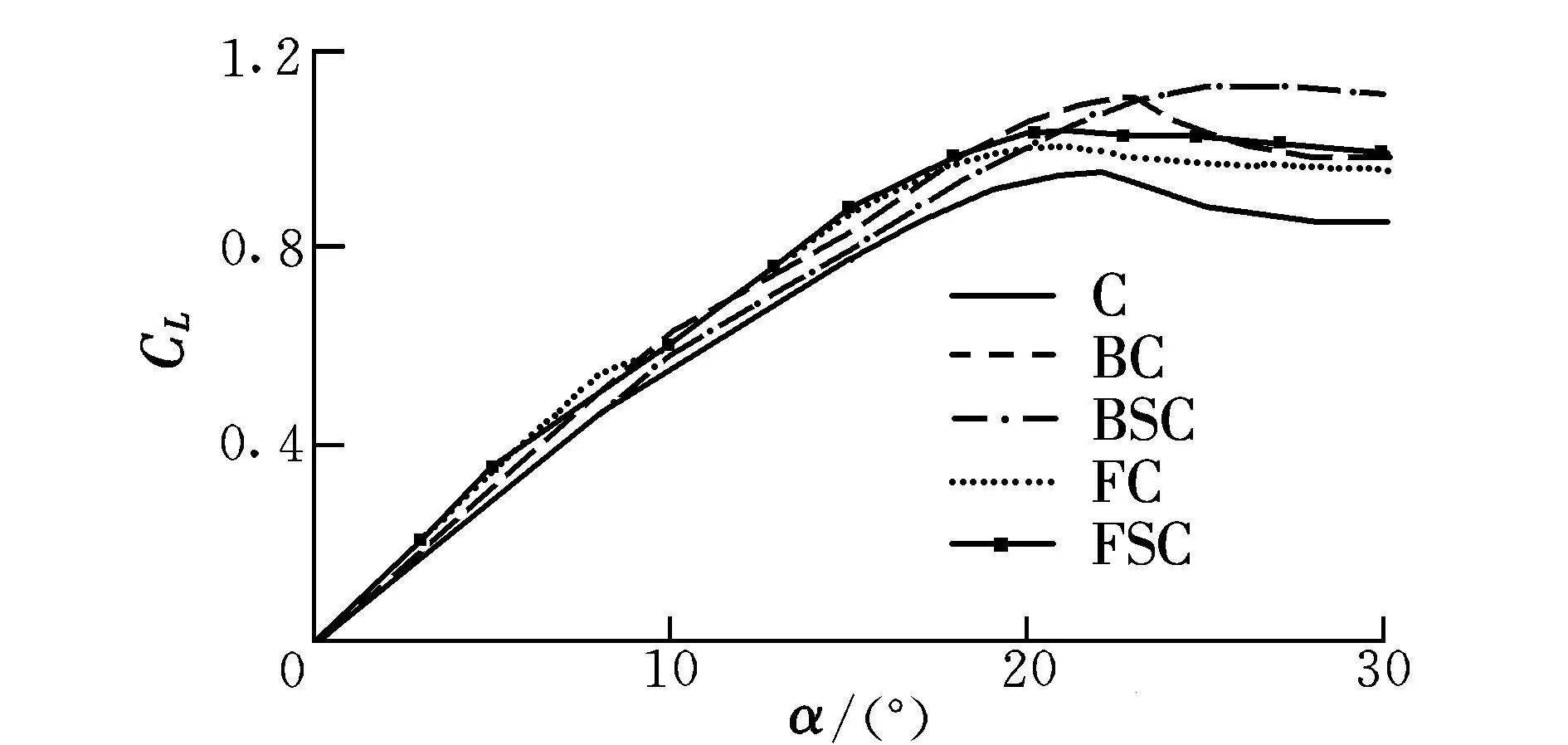
图3　升力系数曲线Fig.3　Lift coefficient curves

3.2单独鸭翼布局

对于在中小迎角下的单独鸭翼,鸭翼涡随着迎角的增加而增强,对翼面的控制范围也逐渐扩大,升力系数随迎角增加呈线性增长;当迎角继续增加,鸭翼涡涡核开始从后向前破裂,涡核破裂后的漩涡能量下降,但漩涡在不断扩大,对翼面的控制区域也相应扩大,所以升力系数随迎角增加有缓慢的增长;当迎角进一步增加,鸭翼涡涡核破裂至前缘,鸭翼涡对翼面的控制作用达到最大,升力系数达到最高点;当迎角继续增加,鸭翼涡外侧气流能量下降,对翼面的控制能力减弱,升力系数下降,鸭翼进入失速状态;进一步增加迎角情况下,鸭翼涡外侧气流破散,气流出现大规模倒流,升力系数明显下降,失速进一步恶化。

图4给出了不同迎角下鸭翼涡的发展变化。为方便对比,本文所有布局都采用相同的压力云图,图例分布如图4左侧所示,后面的压力云图都采用相同的图例分布。

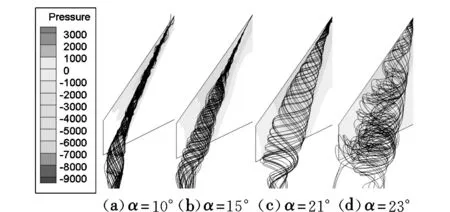
图4　鸭翼空间流线图Fig.4　Streamlines of canard

可以看出:迎角10°时,鸭翼涡涡核开始从后缘破裂;当迎角15°时,涡核破裂至鸭翼中部;当迎角达到21°时,涡核破裂至前缘,升力系数达到最大;继续增大迎角至23°,鸭翼涡破裂,鸭翼进入失速状态。

3.3后掠翼鸭式布局

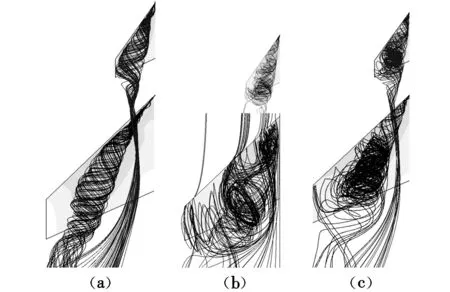
图5　BC布局的空间流线图Fig.5　Streamlines of BC configuration

图5为BC布局的空间流线图。图5(a)给出了迎角23°时的情况,可以看到BC布局中的鸭翼涡和机翼前缘涡都保持稳定状态,而此时单独鸭翼和单独后掠机翼的漩涡早已破裂,如图5(b)所示。当迎角继续增加,两涡能量减小,漩涡破裂,鸭翼出现明显失速,如图5(c)所示,在25°迎角时,鸭翼涡和机翼前缘涡都已破裂。

图6为机翼70%翼根弦长位置上的截面流线图。可以看出：鸭翼涡与机翼前缘涡相互切洗,且有卷绕的趋势,所以两涡能量得到加强,漩涡变得稳定。

图6　截面流线图Fig.6　Streamlines on cross section

3.4带边条后掠翼鸭式布局

图7为不同迎角下BSC布局的空间流线图。可以看出：在25°迎角时,边条涡和机翼前缘涡相互卷并,卷并后的漩涡能量得到增强,变得更加稳定,与鸭翼涡的有利诱导作用更加明显。一方面,鸭翼涡控制着卷并后的漩涡向机翼前缘破裂的速度减慢,使之变得更加稳定;另一方面,卷并后的漩涡对鸭翼涡形成有利干扰,使鸭翼涡变得稳定不易破裂,并在很大迎角范围仍可保持较大的升力系数,且无明显失速。在28°迎角时,鸭翼涡依然比较稳定,还未破裂,只是能量有所减小,升力系数稍有下降,但没有出现明显失速,直到30°迎角时,鸭翼涡才开始破裂。

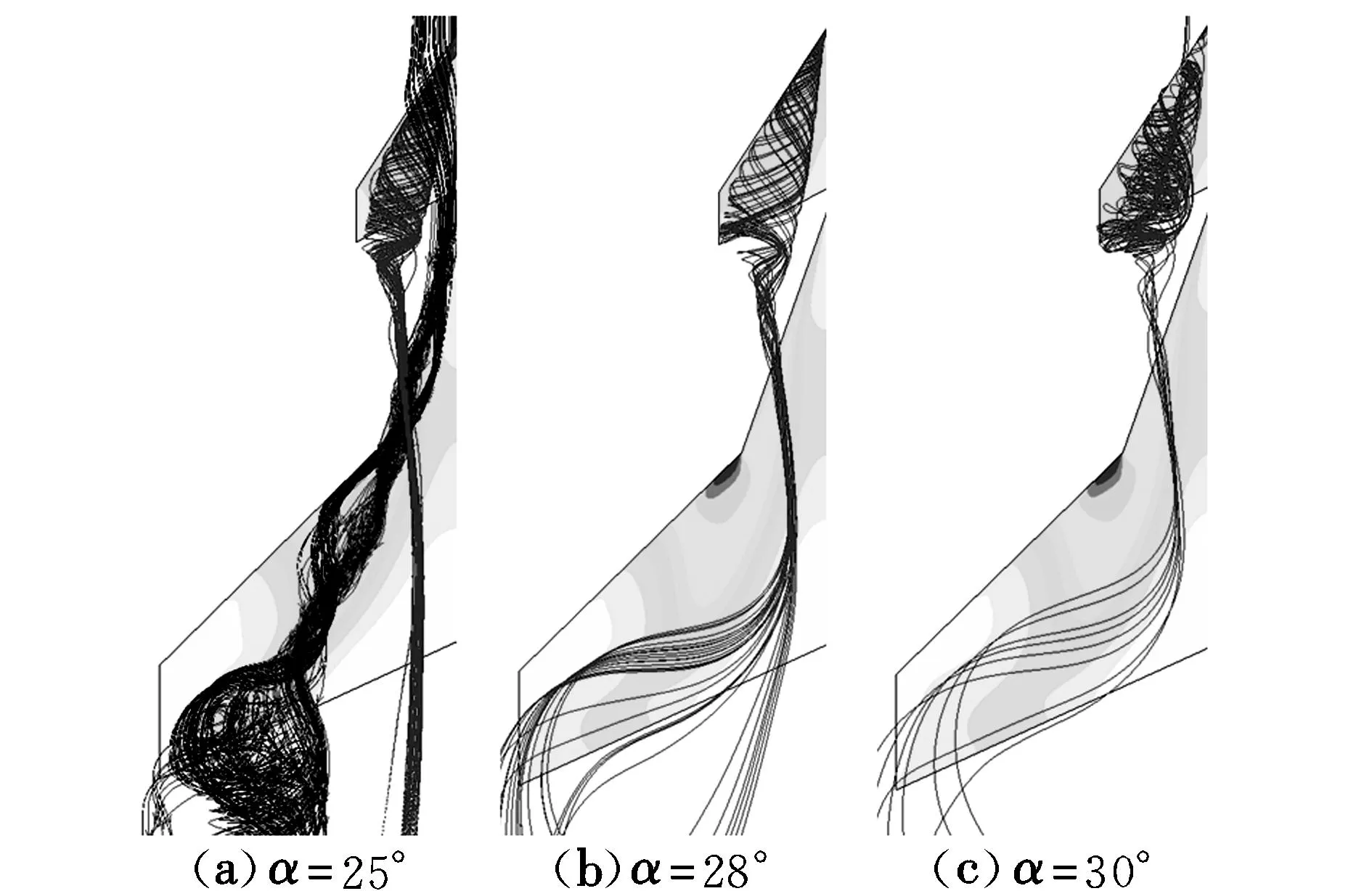
图7　BSC布局的空间流线图Fig.7　Streamlines of BSC configuration

3.5前掠翼鸭式布局

对于FC布局,机翼前缘涡对鸭翼涡存在两方面的作用,图8给出了15°迎角时FC布局和单独鸭翼及机翼的空间流线图。可以看出:FC布局中的机翼前缘涡和鸭翼涡呈一定角度发展,鸭翼涡对机翼前缘涡产生外推和挤压作用,机翼前缘涡不能正常发展,对翼根处的控制作用降低;反过来,机翼前缘涡的上洗作用也阻碍着鸭翼涡的向后流动,形成两涡之间的不利干扰。

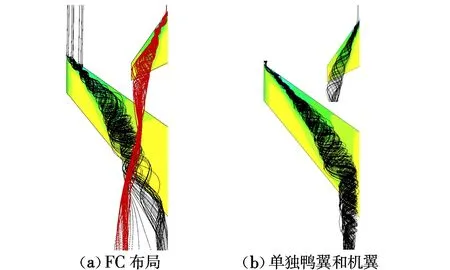
图8　FC布局和单独部件的空间流线图Fig.8　Streamlines of FC and single canard and wing configuration

图9为15°迎角时FC布局中机翼20% 翼根弦长位置上的截面流线图。可以看出:此时鸭翼涡绕至机翼前缘涡上方,由于两涡旋转方向相反,相互切洗,能量有所增强,形成两涡之间的有利干扰。

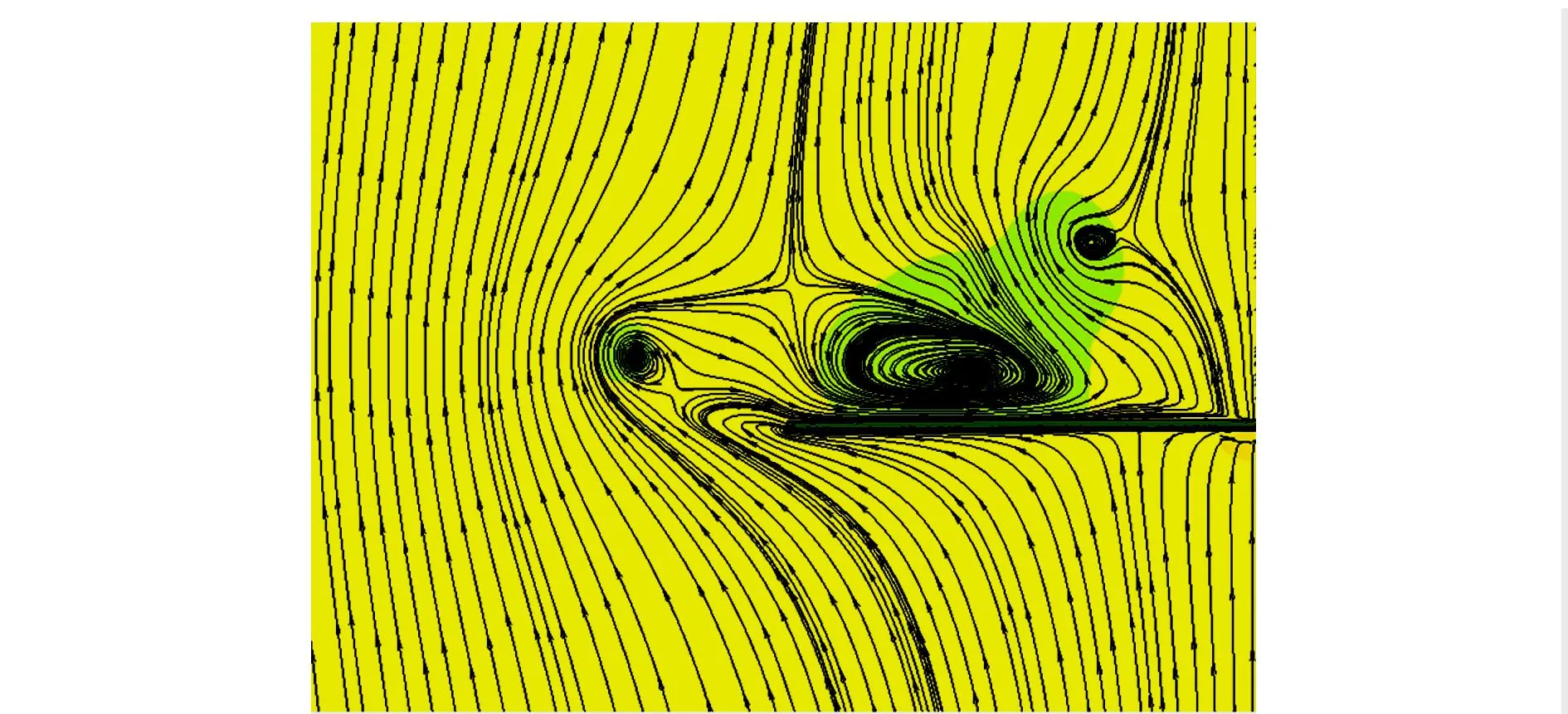
图9　截面流线图Fig.9　Streamlines on cross section

图10为不同迎角下FC布局的空间流线图。可以看出:21°迎角时,鸭翼升力系数达到最大,鸭翼涡涡核已经破裂至前缘且涡核出现倒流,而单独鸭翼涡依然保持稳定,涡核没有出现倒流,这是因为鸭翼涡在发展的过程中遇到机翼前缘涡的不利干扰,但当鸭翼涡绕到机翼前缘涡上方时,两涡相互切洗,使得鸭翼涡外侧气流能量有所提高,所以整个鸭翼涡并没有迅速破裂,还在一定程度上保持稳定;迎角增大到23°时,鸭翼涡外侧气流能量降低,整个鸭翼涡破裂,升力系数下降。

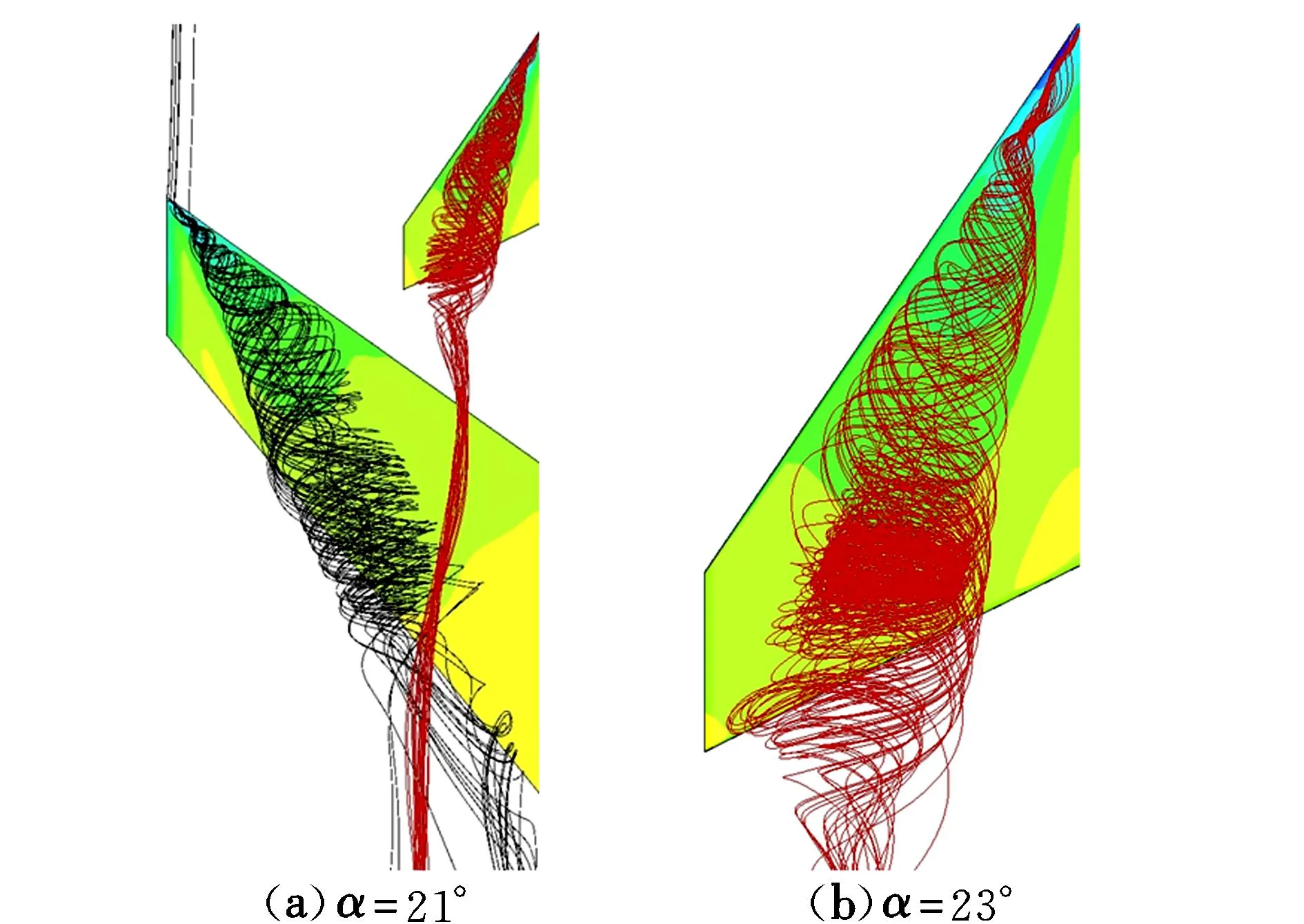
图10　FC布局的空间流线图Fig.10　Streamlines of FC configuration

3.6带边条后掠翼鸭式布局

对于FSC布局,鸭翼涡也受到两方面的影响:一方面鸭翼涡外侧气流受到边条涡的卷绕,能量有所提高;另一方面从鸭翼涡涡核发展来的气流受到机翼前缘涡及绕机翼前缘涡流动的气流的上洗作用,阻碍鸭翼涡的发展,导致鸭翼涡能量下降。两方面的共同作用使得鸭翼涡最大升力系数有所提高,而失速迎角基本保持不变。

图11为不同迎角下FSC布局的空间流线图。可以看出:21°迎角时,鸭翼升力系数最大,边条卷绕着鸭翼涡外侧气流,增大了鸭翼涡能量,而鸭翼涡中心的气流则受到后面气流上洗的不利影响;迎角增大到23°时,鸭翼涡涡核出现倒流,升力系数开始下降。

4结束语

本文通过数值计算,对比研究了前后掠鸭式布局中鸭翼涡的发展过程,分析了机翼前缘涡对鸭翼涡的干扰作用,得到以下结论:

(1)在后掠翼鸭式布局中,鸭翼涡在大迎角时受到机翼前缘涡的有利干扰,增大了鸭翼的升力系数,提高了失速迎角,尤其是带边条后掠翼鸭式布局的效果非常明显。

(2)在前掠翼鸭式布局中,鸭翼涡在大迎角时受到有利和不利两方面的干扰,鸭翼的最大升力系数有所提高,失速迎角基本不变。

参考文献：

[1]Er-El J,Seginer A.Vortex trajectories and break down on wing-canard configurations [J].Journal of Aircraft,1985,22(8):641-648.

[2]Er-El J.Effect of wing/canard interference on the loading of a delta wing [J].Journal of Aircraft,1988,25(1):18-24.

[3]Richard M H,John F O.Flow field study of a closed-coupled canard configuration [J].Journal of Aircraft,1994,31(4):908-914.

[4]刘沛清,魏园.在近距耦合鸭式布局中的涡系结构[J].实验流体力学,2005,19(3):85-89.

[5]Behrbohm H.Basic low speed aerodynamic of short-coupled canard configuration of small aspect ratio[R].SAAB,TN-60,Linko-ping,Sweden,1965.

[6]马宝峰,邓学蓥,刘沛清.近距耦合鸭式布局气动研究进展[J].空气动力学学报,2012,38(7):320-329.

[7]于冲,王旭,董福安.y+值对翼型气动参数计算精度的影响研究[J].空军工程大学学报(自然科学版),2012,13(3):25-29.

[8]王福军.计算流体动力学分析[M].北京:清华大学出版社,2004:31-35.

[9]刘沛清,王亚平,刘杰,等.近距耦合鸭式布局复杂涡系的干扰机理[J].北京航空航天大学学报,2003,21(3):873-881.

[10]李人宪.有限体积法基础[M].北京:国防工业出版社,2008:67-73.

(编辑：崔立峰)

Flow mechanism of canard vortex over forward and backward-swept wing configurations

ZHANG Dong, HU Meng-quan, WANG Xu, WU Zhang-yuan

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

Abstract:Based on simplified models of forward and backward-swept wing configuration, numerical investigation on the vortical structure was carried out by solving Reynolds averaged Navier-Stokes (N-S) equations, and obtained the lift coefficient curves of canard on different configurations. The characteristics of the vortex over single canard and the vortex interaction mechanisms of canard vortex and main wing vortex were analyzed by streamlines. The analysis indicates that the main wing vortex would perform a favorable impact on the canard vortex at high AOA region for backward-swept wing configuration,which enhanced the lift coefficient and increased stall angle of attack. The lift coefficient is also enhanced for forward-swept wing configuration, while the stall angle of attack remains unchanged.

Key words:canard configuration; canard vortex; flow mechanism

中图分类号：V211.3

文献标识码：A

文章编号：1002-0853(2016)01-0036-04

作者简介:张冬(1990-)，男，四川遂宁人，硕士，研究方向为飞行器设计及气动仿真。

基金项目:国家自然科学基金资助(11402301)；航空科学基金资助(20110596007)

收稿日期:2015-05-25;

修订日期:2015-09-21; 网络出版时间:2015-09-29 12:56