孤岛模式运行下含潮汐发电和电池储能的微电网可靠性评估

刘明君，李文沅，王财胜

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400030；2.韦恩州立大学 电气与计算机工程系，美国 底特律 48202）

0 引言

近年来，随着风力发电、光伏发电以及海洋能发电技术［1-2］的发展和应用，基于风力发电、光伏发电和潮汐发电等可再生能源所占的发电比例也越来越高［3］。微电网［4-5］是将可再生新能源发电机组、储能装置、控制装置及负荷等合理配置并接入到电网中的技术。微电网既可以与电网联网运行，也可以与主网断开形成孤岛运行。其灵活的运行方式必将使其成为可再生新能源综合利用的最有效方式之一［6］。我国一直在推动海岛建设，合理利用海洋资源。但在许多远离大陆的海岛，因难以与大规模电网相联，组建离网型微电网成为满足用户负荷需求的选择。同时，这些海岛地区在化石燃料供给上存在巨大困难且运输成本较高，但其周围潮汐资源丰富，因此，发展以潮汐能发电为主的微电网系统不仅能够做到就地取材以充分利用潮汐资源，还能够做到绿色环保。

潮汐流式发电技术通过捕获海水潮涨、潮落产生的动能发电，因此，具有绿色环保无污染、发电无噪声、对海洋生态环境影响小、功率密度大、发电规律性强等优点，赢得了广泛的关注和认可［7］。全球范围内已有很多试验项目正在进行［1-2］；同时，许多发电设备制造厂商研发并制造了可安装于海底的海基潮汐流式发电机［8-9］。在地理资源上，我国海岸线长，潮汐流能资源丰富，并且东部沿海地区经济发达，电力负荷密集，这在客观上为潮汐流能的大规模开发利用创造了有利条件。在国家政策层面上，《国家应对气候变化规划（2014—2020 年）》［10］等多个国字头文件中，都明确提到要大力发展各类潮汐能发电。潮汐流虽有涨落规律性的特点，但这个规律性有不同模式，因而不是完全确定性的；同时在每个时段上潮汐流的大小也存在随机性。因此，如果没有其他备用电源与之组成微电网系统，只依靠潮汐发电并不能保证供电可靠性。电池储能装置的优点是不需要其他一次能源，可以利用潮汐涨落的特点，在潮汐电力富余时储能，而在潮汐电力缺乏时作为备用电源释放电能。然而，作为新型的发电技术，含潮汐发电和储能装置的微电网定量可靠性评估还鲜有文章报道。潮汐流式发电机虽与风力发电机存在众多相似之处，但两者的运行条件以及能源特性均有所不同。因潮汐流和风速产生的机理不同，它们的变化模式亦不相同。潮汐流既有涨落潮的模式规律性，又有每个时段内的随机性，而风速只存在随机性，没有类似于涨落潮那样的模式规律性。对潮汐流而言，需要同时模拟其规律性和时段上的随机性，这就使得风速和潮汐流速的概率建模方法有所不同。因此，需要针对潮汐流式发电机组建立一种能够结合发电机组可用率以及潮汐流速概率特性的可靠性模型。

到目前为止，国内外对于含新能源微电网的可靠性研究不多。文献［11］利用解析方法对含有风－柴储能系统的混合系统进行了可靠性评估，但并未考虑储能系统时序特性。文献［12］初步探索了分布式电源概率模型，但模型较为粗略。文献［13］分析了微电网中可再生能源分布式电源的间歇性对供电可靠性的影响。文献［14］建立了潮汐流式发电机的概率输出模型，但并未涉及可靠性评估。文献［15］评估了孤岛运行下含可再生能源分布式发电的配网系统可靠性，文中利用分段和灰色预测技术对风速进行了预测，但这种技术并不适用于潮汐流速的预测。文献［16］分析了微电网孤岛系统稳定运行、能量供求平衡的机理和常规的微电网孤岛能量管理控制策略，提出了一种新型超级电容与蓄电池混合储能系统的功率自适应控制策略。

本文提出一种针对含潮汐发电和电池储能的微电网可靠性评估模型。建立了结合潮汐流式发电机组可用率和潮汐流速概率特性的多状态模型。同时，根据负荷、电池储能系统性能参数和潮汐流式发电机输出特性建立了电池储能系统输出模型。将此方法应用到假设微电网系统中，计算微电网可靠性指标，并对影响可靠性指标的因素进行分析。研究结果对含潮汐发电的微电网系统设计具有参考性。

1 含潮汐发电和电池储能的微电网可靠性测试系统

本文假定用于可靠性评估的含潮汐发电和电池储能的微电网主要由潮汐流式发电机组、电池储能系统、负荷、联络线以及控制装置组成，见图1。微电网中可以含1台或多台潮汐流式发电机组，组成潮汐发电场。微电网一般有2种运行模式：联网运行模式和孤岛运行模式。联网运行时，当发生潮汐发电输出功率不足时，微电网系统既可以从电池储能系统获得电能，也可以从电网中获得电能。此种运行模式下，电池储能系统运行策略一般为运行于特定的充/放电功率下。在孤岛模式下，电池储能系统需要时刻维持系统的电压和频率稳定，因此，电池的充/放电功率由发电机组输出功率和负荷共同决定。

图1 微电网可靠性测试系统Fig.1 Microgrid system for reliability test

2 潮汐流式发电机组多状态模型

2.1 潮汐流速概率分布模型

潮汐流速随时间变化而变化，而且变化行为因扰流、波浪、风驱海流等因素存在随机性。因此，潮汐发电机组输出功率也存在一定的随机性。根据文献［17］，潮汐流速概率分布服从Wakeby分布。与其他分布不同，Wakeby分布并没有显式表达式，其由5 个参数确定，定义式为［17］：

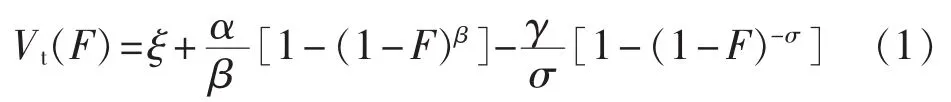
其中，Vt（F ）为潮汐流速；F=F（V）=p（Vt≤V）为 Wakeby分布的累积概率密度函数；α、β、γ、σ、ξ为 Wakeby分布的5个参数，可以根据历史数据利用L阶矩法求得，详细求解步骤可参见文献［17］。此分布用来得到潮汐流速在某个区间段内的概率，结合此概率值和机组可用率建立潮汐流式发电机多状态模型。

2.2 潮汐流式发电机组功率输出模型

潮汐流式发电机组的功率输出Pout可表示为［14］：

其中，Vt、Vcutin、Vrated分别为潮汐流速、潮汐流式发电机组切入速度和额定速度；Cp为潮汐流式发电机组能量捕获因数，一般取 0.4～0.5［14］；ρ为海水密度；A为潮汐流式发电机组叶片扫过的区域面积；Prated为潮汐流式发电机组额定输出功率。

潮汐流式发电机组功率输出特性曲线如图2所示，其可分为3段：第1段为潮汐流速小于切入速度，此时输出功率为0；第2段为潮汐流速大于等于切入速度而小于额定速度，此时输出功率随潮汐流速增加而增大；第3段为潮汐流速大于等于额定速度，此时在控制系统控制下，潮汐流式发电机组输出功率保持额定功率输出。因潮汐流速变化较为缓慢，且最大流速值不足以对发电装置造成破坏，因此已经假定潮汐流式发电机组不存在切出速度。

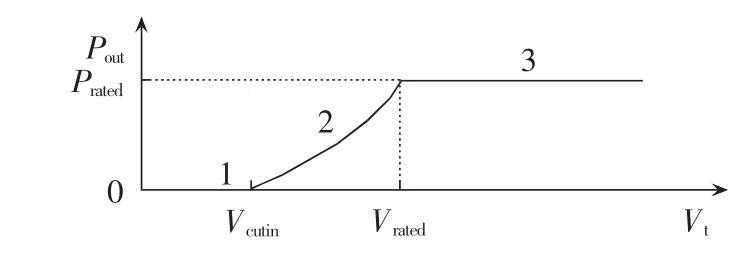
图2 潮汐流式发电机组功率输出特性曲线Fig.2 Characteristic curve of power output of tidal power unit

2.3 潮汐流式发电机组状态模型

潮汐流式发电机组功率输出不仅与机组可用率（AT）有关，还与潮汐流速概率特性有关。因此，潮汐流式发电机组处于某一状态的概率等于潮汐流速处于某一范围内的概率乘以机组的可用率（或不可用率）。根据潮汐流式发电机组功率输出特性可将潮汐流速分为 0＜Vt＜Vcutin、Vcutin≤Vt＜Vrated和 Vt≥Vrated3段，潮汐流速在Vcutin≤Vt＜Vratd范围内变化时，机组输出功率在0到Prated区间内变化，变化范围较大。因此，包括超过额定流速和低于切入流速的情况在内，本文把潮汐流速分为7个状态，旨在保证计算精度的同时提高计算速度。利用状态枚举法建立如表1所示潮汐流式发电机组多状态模型。

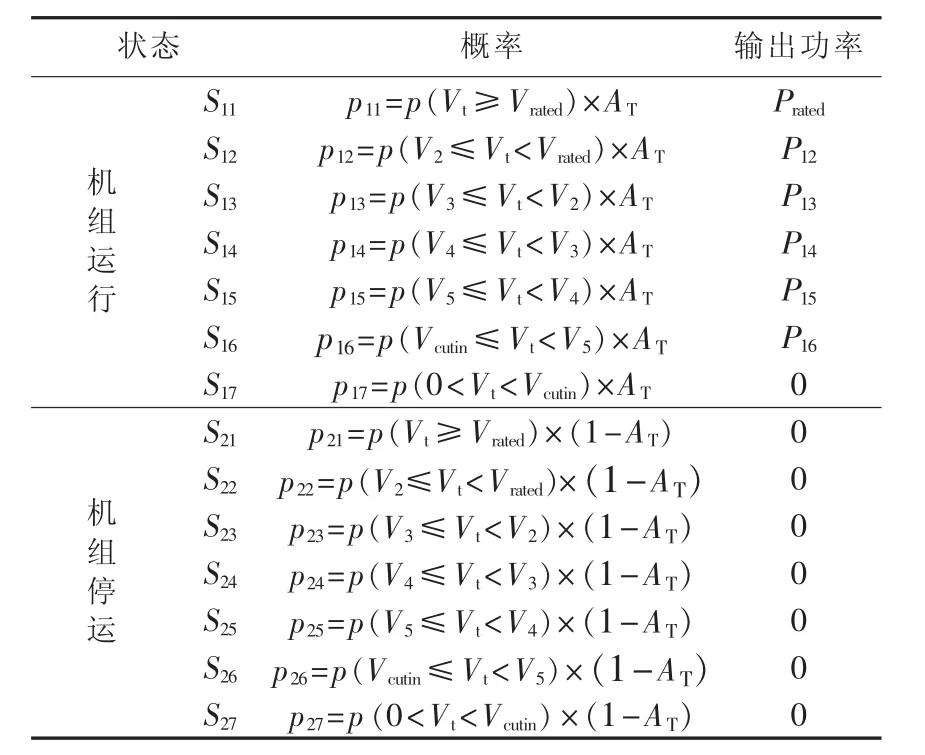
表1 潮汐流式发电机组状态模型Table 1 State model of tidal power unit

表1中，Sij下标i=1表示机组处于运行状态，i=2表示机组处于停运状态；pij表示机组处于某一区间段内的概率；P1j表示潮汐流速在Vcutin到Vrated区间内变化时对应潮汐流速变化区间［Vj，Vj-1］内机组平均输出功率。 令V1=Vrated，V6=Vcutin，P1j计算式为：

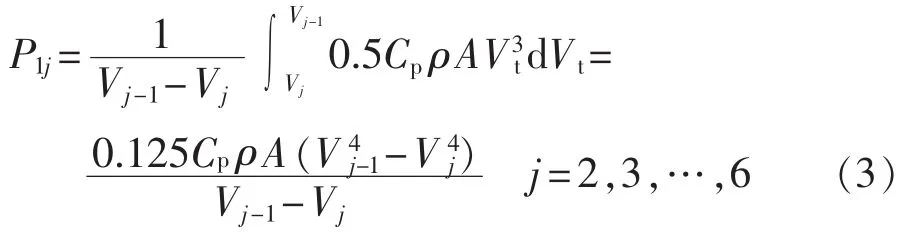
潮汐流速处于某一区间内的概率可以通过以下公式求得：

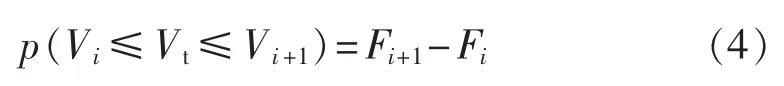
其中，Fi和 Fi+1根据式（1）计算。

由表1可以看出，潮汐流式发电机组存在14个状态、7个功率输出水平，因此，可将潮汐流式发电机组功率输出为0的状态合并，即可得到潮汐流式发电机组状态简化模型，如表2所示。

由于要模拟负荷和储能装置的时序特征，同时每个季节内潮汐流有24 h的周期且每小时有不同的分布参数，因此需要根据以上模型获得潮汐流速在每个季节相同时段的概率分布参数，并将此24段在每个季节内重复，最终得到8760个时段，然后再在每个季节每个时段中建立如表2所示潮汐流式发电机组7状态模型。

表2 潮汐流式发电机组状态简化模型Table 2 Simplified state model of tidal power unit

3 负荷模型及电池储能系统输出功率模型

3.1 负荷模型

发电系统可靠性评估中最常用的负荷模型为时负荷值曲线模型［18-19］，此负荷模型基于IEEE Power Engineering Society设计的IEEE-RTS负荷模型，修改其系统年峰值负荷得到。负荷模型可由下式表示：

其中，PL为微电网负荷；Pmax为微电网年度峰值负荷；Pweek、Pday和Phour分别为周负荷峰值模型、日负荷峰值模型和时负荷峰值模型。PL含有8 760个时段。此负荷模型考虑了负荷因季节变化引起的变动，因此相对较为精确。

3.2 电池储能系统输出功率模型

因潮汐流式发电机组输出功率和负荷都存在随机性，孤岛模式运行时，微电网不能通过电网获得电能，只能依靠自身维持系统稳定，而机组输出的功率并不能时刻满足负荷需求。因此，在无其他外部电源的条件下，为了维持系统可靠性，安装电池储能系统是一个较好的选择。微电网在孤岛模式运行时，电池储能系统充/放电功率通过电压/频率稳定方案控制，以平衡系统负荷需求与机组输出功率。联网模式下，电池储能系统充/放电功率可以根据预设值运行，以提高电池储能系统寿命［20］。本文只研究微电网孤岛运行模式下系统可靠性评估。

孤岛模式下，负荷需求由电池储能系统和潮汐流式发电机组共同满足，在潮汐流式发电机组输出功率大于负荷需求时，多余的电量为电池储能系统充电，反之，电池储能系统放电。因此，第k个时间段内机组第s个状态下系统能够为电池储能系统提供或需要电池储能系统放电的功率 Pbat，s（k）可由下式计算：

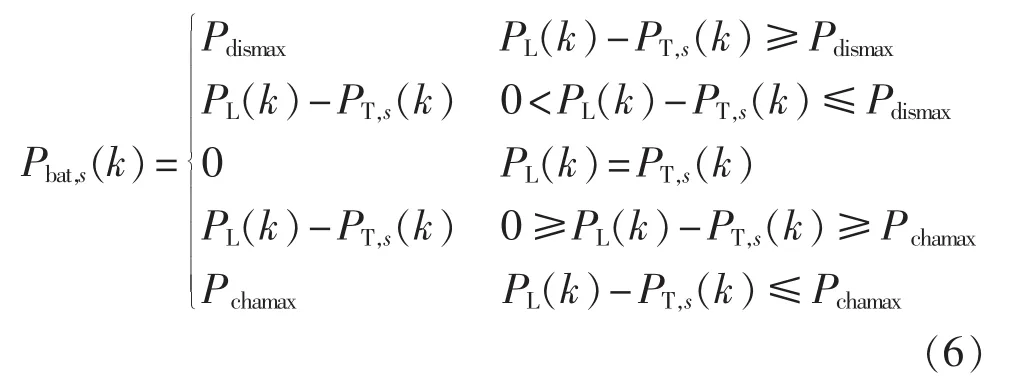
其中，Pdismax、Pchamax分别为电池储能系统最大放电和充电功率（用负数表示）；PL（k）为第k个研究时间段内负荷功率；PT，s（k）为潮汐流式发电机组在第 k 个研究时段内第s个状态下的输出功率。值得注意的是，式（6）中仅仅考虑了电池储能系统最大充/放电功率的限制，但所得结果并不是实际发生的充/放电功率。考虑到实际运行中电池储能系统充/放电功率不仅受电池储能系统最大充 /放电功率的约束，还受电池储能系统正常运行允许的最大和最小储存容量的约束。这种储存容量可以转换为等效充/放电功率约束。考虑最小储存容量Qmin约束的等效电池储能系统放电功率为：

其中，Pedismax（k）为第k个研究时段内对应的最小储存容量约束下的等效放电功率；Qbat（k）为电池储能系统在第k个研究时段的储存容量。

类似地，考虑最大储存容量Qmax约束的等效电池储能系统充电功率为：

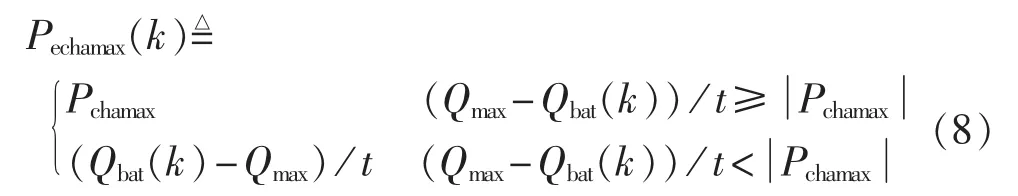
其中，Pechamax（k）为第k个研究时段内对应的最大储存容量约束下的等效充电功率。需要注意的是Pechamax（k）和Pchamax都为负值，表示电池储能系统充电模式。

式（6）计算得到的 Pbat，s（k）为第 k 个研究时段内第s个状态下为维持系统发电和负荷的需求平衡，系统可以为电池储能系统充电或可以从储能系统获得的功率，并非储能系统实际充/放电功率。而储能系统的实际充/放电功率还应受到式（7）和式（8）的约束。换言之，储能系统的实际放电功率应该在Pbat，s（k）＞0 和 Pedismax（k）之间，取两者最小值。 类似地，电池储能系统的实际充电功率应限制在Pbat，s（k）＜0和Pechamax（k）之间，因本文用负数表示充电功率，因此，需要取两者的最大值，即绝对值最小。上述逻辑关系可用下式表示：

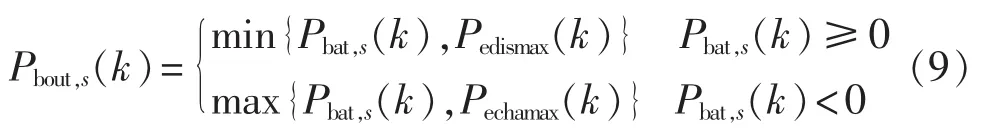
其中，Pbout，s（k）为第 k 个研究时段内第 s个状态下的电池期望输出功率。

因此，第k个研究时段内电池储能系统充/放电功率期望值为：

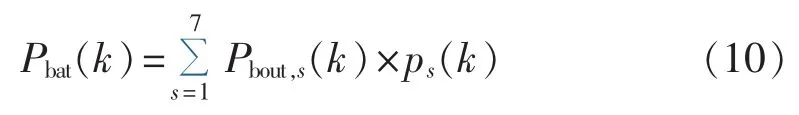
其中，ps（k）为潮汐流式发电机处于第s个状态的概率。当Pbat（k）＞0时，电池储能系统处于放电状态，此时可作为电源看待；当Pbat（k）=0时，电池储能系统处于待机状态；当Pbat（k）＜0时，电池储能系统处于充电状态，此时可作为负荷看待。电池储能系统在第k+1个研究时段内的储存容量可由第k个研究时段的储存容量和该时段内的电池充/放电能量计算，公式如下：

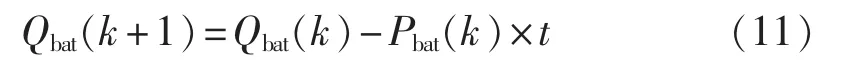
其中，t为研究时段k的长度，本文取t=1h。

4 可靠性指标及其计算

电池储能系统可用与否影响着微电网可靠性指标。考虑实际情况，其运行与失效只需在每个时段机组每个状态下再枚举电池失效与否即可。与主网联接的线路不可用率决定了微电网孤岛运行的概率。注意，潮汐流式发电机组的可用率AT已经在机组的状态枚举模型中考虑。因此，考虑电池储能系统可用率和形成孤岛概率的微电网系统可靠性指标计算如下。

4.1 电力不足期望

电力不足期望LOLE（Loss Of Load Expectation）可由下式计算［19］：

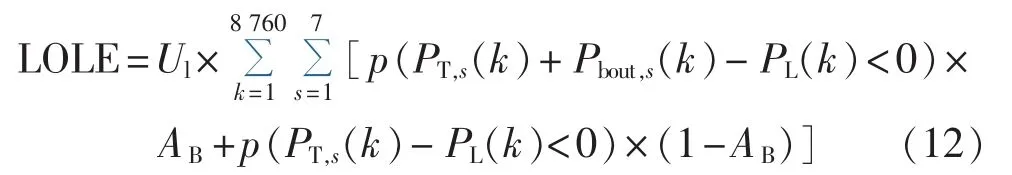
其中，p（·）为满足括号内条件的概率；AB、Ul分别为电池储能系统的可用率和联络线不可用率。

4.2 期望缺供电量

期望缺供电量EENS（Expected Energy Not Supplied）可由下式计算［19］：

其中，CBU，s（k）、CBD，s（k）分别为第 k 个研究时段内机组第s个状态下电池运行和失效时的切负荷量；ps（k）为对应的切负荷概率。

4.3 计算步骤

本文计算可靠性指标的步骤如下。

（1）将潮汐历史流速数据分为4个季节，并求取每个季节相同时段（24个）潮汐流速概率分布参数；在每个季节每个时段内，根据表1和表2建立潮汐流式发电机组多状态模型；在每个季节内再将24个时段重复每个季对应的天数，最后得到4个季节总共8760个时段中每个时段的潮汐流式发电机组多状态模型。从而将潮汐发电机组输出功率因季节变化引起的变动考虑在内。

（2）由式（5）获得一年负荷数据 PL，由式（6）—（11）计算电池储能系统在第k个研究时段内机组所有状态下的输出功率。

（3）计算可靠性指标。在每个时段每个机组状态下枚举电池失效与否，并计算相应状态下可靠性指标，最后由式（12）和（13）计算微电网系统8760个时段可靠性指标。

5 算例分析

本文使用的潮汐流速数据由美国国家海洋和大气管理局官方网站获得，采集地点为Golden Gate Bridge，其位于美国西海岸，位置坐标为（北纬37.82°，西经122.45°），潮汐流速数据时间间隔为10 min，时间段为2010年1月1日至2013年12月31日。本文假设所研究微电网系统含有1台额定容量1.5 MW的潮汐流式发电机组，其切入速度和额定速度分别为1.2 knots和3.5 knots（knots表示单位节，为专用于航海的速度单位），机组不可用率为0.0354［21］。电池储能系统不可用率设为0.01，假设微电网处于偏僻地区，主网联络线不可用率较高，为0.1。假设图 1所示微电网年峰值负荷为300 kW，电池储能系统性能参数为：Pchamax=-500 kW，Pdismax=300 kW，Qmax=1 500 kW·h，Qmin=0.1Qmax。根据本文计算方法得到微电网系统可靠性指标如表3所示。

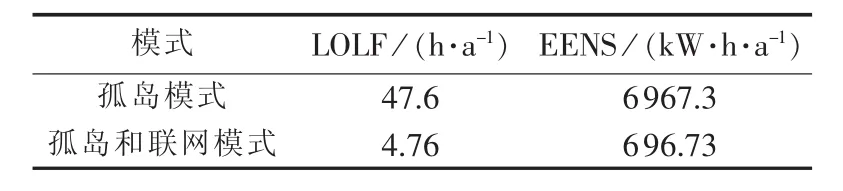
表3 微电网可靠性指标Table 3 Reliability indexes of microgrid

表3中，“孤岛模式”栏表示微电网作为孤立电网不与外部电网相连时全年可靠性指标；“孤岛和联网模式”栏表示微电网与外部电网相连，只在联络线故障时处于孤岛运行的微电网可靠性指标。由表3可知微电网可靠性较高。

5.1 电池储能系统参数对微电网可靠性参数的影响

电池储能系统作为微电网系统中除潮汐流式发电机组以外唯一的电源，其性能参数直接影响微电网可靠性指标。本节研究电池储能系统参数（最大放电功率Pdismax、最大充电功率Pchamax、电池储能系统最大容量Qmax以及电池储能系统可用率AB）对微电网可靠性指标的影响。电池储能系统的可靠性参数可以从电池储能系统本身的可靠性评估中获得［22］。假设微电网年峰值负荷为300 kW，电池储能系统允许的最小容量为Qmin=0.1 Qmax，电池储能系统可用率为0.99，微电网孤岛运行。令电池储能系统最大充电功率从0增加到500 kW，计算微电网可靠性参数，结果如图3所示。

由图3可得如下结论。

图3 微电网可靠性指标随电池储能系统最大充电功率变化曲线图Fig.3 Curves of microgrid reliability index vs.maximum charging power of battery energy storage system

（1）在电池储能系统最大容量和充电功率一定的情况下，微电网可靠性指标会随最大放电功率的增加而减小，但减小幅度逐渐减弱，特别是当最大放电功率超过微电网年峰值负荷时，微电网可靠性指标保持定值。最大放电功率表示系统能够从电池储能系统中获得的最大功率，当系统负荷超过发电机组输出功率时，系统可以从电池储能系统中获得［0，Pdismax］的功率。因此，其大小可以在一定程度上决定系统是否满足负荷需求。

（2）在电池储能系统最大放电功率和最大容量一定的情况下，提高电池储能系统最大充电功率可适当减小微电网可靠性指标。因电池储能系统最大充电功率反映了电池储能系统在单位时间内储存能量的能力，当发电机组输出功率超过负荷需求时，最大充电功率越大，其能够储存的能量就越多，因此，用于平衡负荷的能量就越多，对微电网系统可靠性贡献就越大。

（3）在电池储能系统最大放电功率和最大充电功率一定的情况下，增加电池储能系统最大容量可以减小微电网可靠性指标。电池储能系统最大容量反映电池储能系统能够储存的容量，其值大小制约着电池储能系统放电总量。

（4）当电池储能系统放电功率较小时，3条曲线重合，这是因为电池储能系统都不能够满足放电需求，但随着放电功率的增加，曲线开始分散，电池储能系统的最大充电功率和最大容量对储能微电网可靠性指标的影响逐渐显现。

（5）当电池储能系统放电功率在200 kW到300 kW范围变化时，下侧图中曲线1略有上升，这是因为随放电功率的增加，较小的电池储能系统容量不能长时间维持电池放电，从而增加切负荷量，增加储能系统容量会显著减小这一趋势（见下侧图中曲线2）。随着容量的增大，最大充电功率作为新的制约因素影响微电网可靠性。

为研究电池储能系统可用率对微电网可靠性指标的影响，使用与计算表3相同的微电网系统数据，并只考虑微电网孤岛运行的情况，计算得到微电网在不同电池储能系统可用率AB下可靠性指标如表4所示。由表4可知，电池储能系统可用率越高，微电网可靠性指标越低，即微电网越稳定。

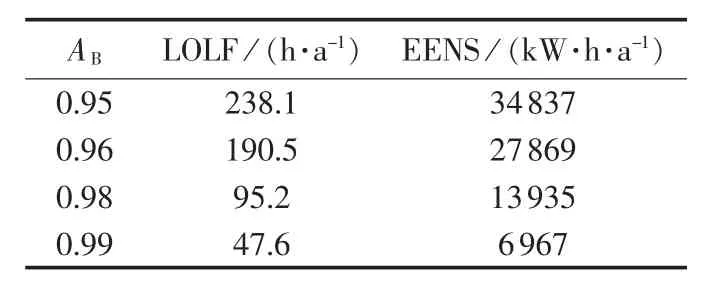
表4 不同电池储能系统可用率下微电网可靠性指标Table 4 Microgrid reliability indexes of different availability levels of battery energy storage system

5.2 年峰值负荷对微电网可靠性指标的影响

本节研究负荷变化对微电网可靠性指标的影响。在潮汐流式发电机组和电池储能系统一定的条件下，负荷的变化会直接影响系统的可靠性。由式（5）可知，负荷的变化由年峰值负荷决定。因此，为研究负荷变化对微电网可靠性指标的影响，令年峰值负荷在100 kW到800 kW范围内变化，计算微电网可靠性指标如图4所示。由图4可知：

（1）当年峰值负荷小于300 kW时，负荷增长对可靠性指标增长贡献较小，因为此时负荷在所假定微电网可带负荷能力范围内；

（2）负荷峰值在300 kW到600 kW范围内变化时，电池储能系统性能参数不同时得到的微电网可靠性指标也不同，提高电池储能系统性能参数可以在一定范围内减小微电网可靠性指标；

（3）当年峰值负荷大于600 kW时3条曲线再次重合，这是因为随着负荷的增大，潮汐发电机组功率输出已不能满足负荷的需求，因此电池储能系统始终处于无法充电状态，无论电池系统性能参数如何提高对微电网可靠性指标都没有贡献。

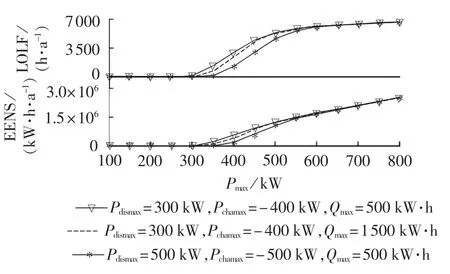
图4 微电网可靠性指标随年峰值负荷变化曲线图Fig.4 Curves of microgrid reliability index vs.yearly peak load

6 结论

本文提出了一种对含潮汐发电和电池储能的微电网可靠性评估模型，并通过对一个该类微电网的可靠性指标计算分析，说明了所提出模型的有效性。与常规机组不同，潮汐流式发电机组的输出状态不仅取决于它的可用率，而且与潮汐流的概率分布强相关。本文提出了结合潮汐流速概率分布特性和机组可用率的多状态模型，并利用枚举法与负荷和储能系统的时序特性相结合，建立了电池储能系统功率充放电输出模型。通过算例研究了电池储能系统参数对含潮汐发电微电网可靠性的影响。本文研究成果可为含潮汐发电和电池储能的微电网系统设计提供参考，特别是为偏远海岛地区电气化的实现提供了一种解决方案。

［1］ROURKE F O，BOYLE F，REYNOLDS A.Tidal energy update 2009［J］.Applied Energy，2010，87（2）：398-409.

［2］KHAN M J，BHUYAN G，IQBAL M T，et al.Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications：a technology status review［J］.Applied Energy，2009，86（10）：1823-1835.

［3］ABBEY C，KATIRAEIF，BROTHERSC，etal.Integrationof distributed generation and wind energy in Canada［C/OL］.Montreal，Canada：IEEE，2006［2015-11-18］.http：∥ieeexplore.ieee.org/document/1709430/.

［4］LASSETER R，ALTHIL A，MARNAY C，etal.Integration of distributed energy resources-the CERTS microgrid concept［EB/OL］.（2010-08-16）［2015-11-18］.http：∥www.pserc.org/ecow/get/researchdo /certsdocum0 /certspubli/certsmicrogridwhitepaper.pdf.

［5］LASSETER R H，PAIGI P.Microgrid：a conceptual solution［C］∥IEEE Power Electronic Specialists Conference.Madison，USA：IEEE，2004：4285-4290.

［6］别朝红，李更丰，王锡凡.含微网的新型配电系统可靠性评估综述［J］.电力自动化设备，2011，31（1）：1-6.BIE Zhaohong，LI Gengfeng，WANG Xifan.Review on reliability evaluation of new distribution system with micro-grid［J］.Electric Power Automation Equipment，2011，31（1）：1-6.

［7］游亚戈，李伟，刘伟民，等.海洋能发电技术的发展现状与前景［J］.电力系统自动化，2010，34（14）：1-12.YOU Yage，LI Wei，LIU Weimin，et al.Development status and perspective of marine energy conversion systems［J］.Automation of Electric Power Systems，2010，34（14）：1-12.

［8］ABB Group.ABB to provide UK grid connection for Europe’s largest tidal energy project［EB/OL］.（2015-09-11）［2015-11-18］.http：∥www.abb.com /cawp /seitp202 /75d122d94ef09aaec1257d3-8002b32f7.aspx.

［9］Alstom Group.Tidalpowersolutions［EB /OL］.（2015-09-11）［2015-11-18］. http：∥www.alstom.com /Global/Power/Resources/Documents/Brochures/tidal-power-solutions-ocean-energy.pdf?epslanguage=en-GB.

［10］国家发展改革委关于印发国家应对气候变化规划（2014—2020年）的通知（发改气候［2014］2347 号）［EB/OL］.（2014-11-25）［2015-11-18］.http：∥www.scio.gov.cn /xwfbh /xwbfbh /wqfbh /2014/20141125 /xgzc32142 /Document/1387125 /1387125.htm.

［11］LIU X，ISLAM S.Reliability evaluation of a wind-diesel hybrid power system with battery bank using discrete wind speed frame analysis［C］∥9th International Conferenceeon Probabilistic Methods Applied to Power Systems.Stockholm，Sweden：［s.n.］，2006：1-7.

［12］袁修广，黄纯，张磊，等.计及微网孤岛运行方式的配电网可靠性评估［J］.电网技术，2015，39（3）：690-697.YUAN Xiuguang，HUANG Chun，ZHANG Lei，et al.Reliability evaluation of distribution network considering islanded operation of microgrid［J］.Power System Technology，2015，39（3）：690-697.

［13］王韶，谭文，黄晗.计及微电网中可再生能源间歇性影响的配电网可靠性评估［J］.电力自动化设备，2015，35（4）：31-36.WANG Shao，TAN Wen，HUANG Han.Distribution system reliability evaluation considering influence of intermittent renewable energy sources formicrogrid［J］.Electric Power Automation Equipment，2015，35（4）：31-36.

［14］LIU Mingjun，LI Wenyuan，BILLINTON R，et al.Probabilistic modeling of tidal power generation［C］∥IEEE Power Energy Society General Meeting.Denver，USA：IEEE，2015：1-5.

［15］ATWA Y M，EL-SAADANY E F.Reliability evaluation for distribution system with renewable distributed generation during islanded mode of operation［J］.IEEE Transactions on Power Systems，2009，24（2）：572-581.

［16］李斌，宝海龙，郭力.光储微电网孤岛系统的储能控制策略［J］.电力自动化设备，2014，34（3）：8-15.LI Bin，BAO Hailong，GUO Li.Strategy of energy storage control for islanded microgrid with photovoltaic and energy storage systems［J］.Electric Power Automation Equipment，2014，34（3）：8-15.

［17］LIU Mingjun，LI Wenyuan，BILLINTON R，et al.Modeling tidal current speed using Wakeby distribution［J］.Electric Power System Research，2015（127）：240-248.

［18］SCHNEIDER A W.The IEEE reliability test system-1996［J］.IEEE Transactions on Power Systems，1999，14（3）：1019-1020.

［19］LI Wenyuan.Risk assessment of power systems［M］.2nd ed.New York，USA：IEEE and John Wiley&Sons，2014.

［20］BHUIYAN F A，YAZDANI A.Multimode control of a DFIG-based wind-power unit for remote applications［J］.IEEE Transactions on Power Delivery，2009，24（4）：2079-2089.

［21］LIU Mingjun，LI Wenyuan，WANG Caisheng，et al.Reliability evaluation of tidal power generation system considering tidal current speed［J］.IEEE Transactions on Power Systems，2016，31（4）：3179-3188.

［22］LIU Mingjun，LI Wenyuan，WANG Caisheng，et al.Reliability evaluation of large scale battery energy storage systems［J］.IEEE Transactions on Smart Grid，2016，PP（99）：1-11.