长距离输电线路中间带并联电抗器的双端非同步故障定位算法

张德泉，罗深增，李银红

（1.国家电网公司华中分部，湖北 武汉 430077；2.华中科技大学 电气与电子工程学院 强电磁工程与新技术国家重点实验室，湖北 武汉 430074）

0 引言

超高压、特高压长距离输电线路分布电容电流很大，通常在线路装设并联电抗器，以补偿容性无功功率，限制工频过电压，同时还具有限制潜供电流、避免产生谐振过电压等优点。并联电抗器通常安装在线路一侧或两侧，从抑制过电压的角度，并联电抗器也可能安装在线路中间［1-2］。对于并联电抗器安装在线路两侧变电站内的情况，通常并联电抗器配置有高精度的电流互感器，将并联电抗器测量电流引入线路电流进行补偿，即可视为普通线路进行故障定位。而对于并联电抗器安装在线路中间的情况，则需要进一步考虑其故障定位问题。

已有部分文献针对带并联电抗器的线路故障定位问题进行了研究。文献［3］基于时域双端同步采样值，提出了无需并联补偿装置模型的故障定位算法，适应于各种并联补偿线路，但该方法需要较高采样频率，且双端时域采样数据具有高同步性。将并联电抗器的电抗视为已知量，文献［4-8］提出了相应的基于双端工频量的故障定位算法。文献［4］基于线路分布参数模型构造定位方程，实现对故障点与并联电抗器安装点之间位置关系的正确判断，即实现伪根的判别。文献［5］将线路参数与故障距离均视为未知量，构造线路故障网络频谱方程，从而得到故障点位置。针对串联电容补偿线路和并联电抗器补偿线路，文献［6］提出了考虑双端数据不同步的故障定位算法。文献［7］提出了基于纵向阻抗的双端故障定位算法，在线计算出系统阻抗和线路参数，对于带并联电抗器的线路，将并联电抗器的影响在线路π型等值模型中进行处理。文献［8］研究了带并联电抗器的双回线故障定位算法。上述算法将并联电抗器视为参数已知的纯电抗，这种处理思路虽然简单，但是实际中并联电抗器参数与设计参数相比可能发生变化。随着可控并联电抗器技术的发展及应用，并联电抗器的电抗值不再固定，可以根据需要灵活进行调节，并且故障后可控并联电抗器的控制保护系统也可能动作［9-10］，因此已有故障定位算法可能出现失效的情况。

本文对长距离输电线路中间带并联电抗器的故障定位算法进行了研究。对于并联电抗器的等值电抗固定的线路，提出了基于并联电抗器等值阻抗估计的故障定位算法。该方法采用故障前的双端相量估计并联电抗器的实际等值阻抗，从而基于故障后正序网络得到故障点位置。对于可控并联电抗器或故障前数据无法获取的情况，提出了无需并联电抗器模型的故障定位算法。该方法根据不同故障类型的故障边界条件，利用故障点电压、电流的相位特性构造定位函数。所提算法均基于分布参数模型，双端数据不同步角采用故障前或故障后测量相量进行补偿。大量仿真结果表明了所提方法的有效性。

1 基于并联电抗器等值阻抗估计的故障定位算法

线路中间安装一组并联电抗器的正序网络示意图如图1所示。

考虑双端测量数据可能出现不同步的情况，设不同步角为 δ，则有［11-12］：

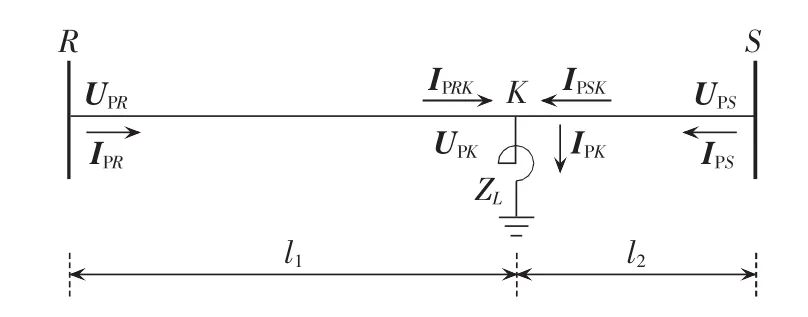
图1 线路中间带并联电抗器正序网络示意图Fig.1 Positive-sequence network of transmission line with shunt reactor in middle

其中，UPS、IPS为数据同步修正后的相量；UPS0、IPS0分别为线路S侧电压、电流测量值。

根据线路分布参数模型，由线路两侧计算得到的并联电抗器安装处电压UPK相等。

其中，l1、l2分别为并联电抗器安装点K与母线R、S的距离；UPR、IPR分别为线路R侧电压、电流测量值；Zc、γ分别为线路特性阻抗、传播常数。将式（1）代入式（2）中，可得：

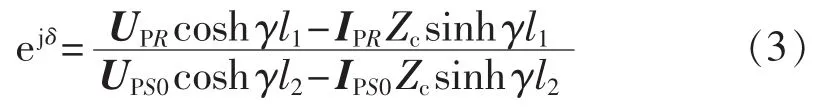
由此，求得双端数据不同步角δ。根据式（1）得到修正后的S侧电压、电流相量。同样，根据线路分布参数模型推算得到线路R、S侧流向并联电抗器的电流分别如式（4）、（5）所示。

流经并联电抗器的电流IPK为：

因此，由式（2）、（4）—（6）计算得到并联电抗器等值阻抗ZL为：

图2 故障正序网络示意图Fig.2 Schematic diagram of positive-sequence network with fault

不妨假设故障发生在并联电抗器左侧F处，与母线R距离为x，故障正序网络如图2所示。图中，UFR、IFR分别为线路R侧电压、电流测量值。UFS0、IFS0分别为线路S侧电压、电流测量值，则经过数据同步修正后的相量UFS、IFS为：

由分布参数模型有：

故障前后并联电抗器的等值阻抗视为不变，有：

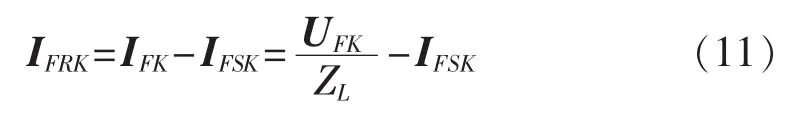
由UFR、IFR以及UFK、IFRK计算故障点F处的电压应相等，因此有：

由式（12）可得故障距离 x 为［13］：

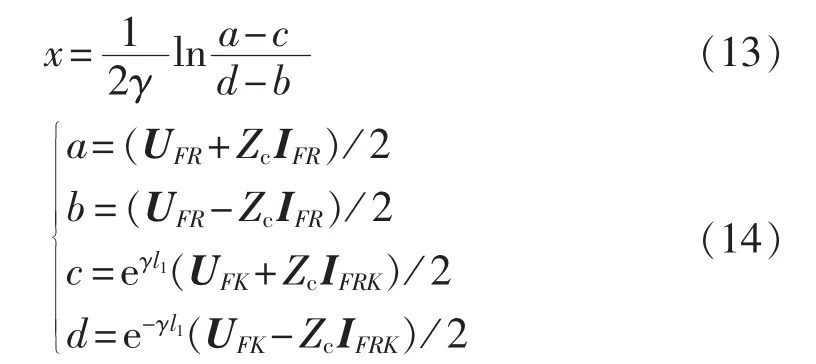
若线路两侧测量数据进行了数据同步补偿，则式（13）得到的x接近于实数，否则x的虚部具有一定值。并且由于采用故障前数据进行了同步补偿，避免了进行数据同步修正而出现伪根的情况［13］。最终的故障距离取x的实部即可。当故障发生在并联电抗器右侧，即在区间（l1，l1+l2）发生故障时，可同样得出类似式（13）的结果。在进行故障定位前并不知道故障点的位置，因此假设在区间（0，l1）、（l1，l1+l2）分别发生故障，求得故障点，但所求故障点应相应在区间（0，l1）、（l1，l1+l2）内，由此可排除相应伪根。

由于采用了故障前的数据对双端数据不同步角以及并联电抗器的等值阻抗进行了估计，故障后只采用正序网络参数即可得到精确的故障距离，无需零序参数、故障类型。但是该方法假设并联电抗器等值阻抗参数在故障前后不变，且需要故障前数据来估计其阻抗。因此，下面将提供另一种无需并联电抗器模型的故障定位算法。

2 无需并联电抗器模型的故障定位算法

并联电抗器的阻抗无法事先估计，因此后续故障定位算法将不使用该参数。考虑如图2所示的故障网络，由于 UFK、UF已求出，因此 IFSF为：

而故障点另一侧电流IFRF为：

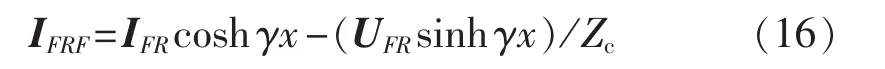
因此，故障通路电流IF为：

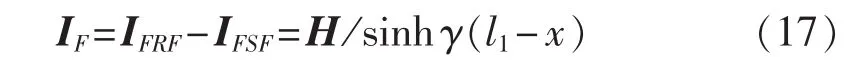
故障通路可视为纯电阻性，即UF和IF相位相等：

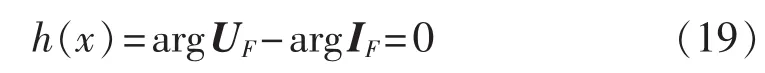
输电线路线路传播参数γ为：

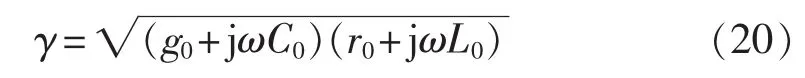
其中，g0、C0、r0和 L0分别为单位长度的输电线路的电导、电容、电阻和电感值。通常对于高压架空输电线路，g0≈0，r0≪ωL0，忽略 g0和 r0，则传播参数 γ=jβ，有：

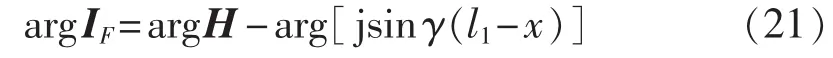
因此，argIF近似为常数。设：－IFRZc=UFRK∠α，则有：

在实际电网中，βx 在（0，π/2）内，UF与 UFR的相位差η为：

系统发生故障后，K、α均为定值，可见η随着x的增加单调变化，即定位函数 h（x）在区间（0，l1）单调变化。因此h（x）快速求根采用二分区间求根法或者弦截求根法即可［14-15］。为避免角度的求取及周期变换，可等价采用式（24）计算h（x）。对于金属性短路故障，故障点电压为0，即UF=0，也有式（24）成立。

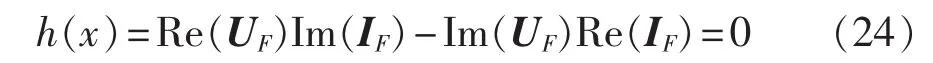
上述讨论基于单相系统，对于三相系统，针对不同故障类型，需要使用电压、电流分量如表1所示［16］。表中，s取 1、2、0 分别表示正、负、零序分量；φφ 取AB、BC、CA分别表示对应线分量。对于两相接地故障（LLG）、相间故障（LL）和三相故障（LLL），采用线路两端线电压、线电流计算UF和IF，特性阻抗及传播常数采用正序参数；对于单相接地故障（LG），分别采用正序、负序、零序分量计算得到和，其中特性阻抗及传播常数应对应正、负、零序参数，UF和IF分别为三序分量之和，如式（25）所示。

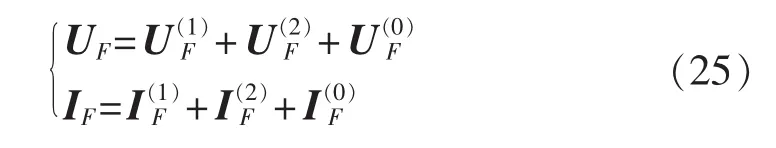
表1 不同故障类型使用的电压、电流分量Table1 Voltage and current components for different fault types

当在区间（l1，l1+l2）内发生故障时，可同样得出类似结果。在进行故障定位时假设在区间（0，l1）、（l1，l1+l2）分别发生故障，求得式（24）的根。 通常，区内故障只在一个区间有根，那么所得式（24）的根即为故障点位置，但是某些情况下也可能在2个区间内均有根，那么可以通过故障距离反推求出并联电抗器模型等效参数以排除伪根。以图2为例有：

以A相接地为例，A相并联电抗器等值阻抗为：

并联电抗器等值阻抗应不超过其最大值，且均为正值，实际中考虑计算误差，应留有一定裕度。其他相并联电抗器等值阻抗可类似得出。由此可排除虚假故障点，得到最终的故障点位置。

对于双端数据不同步角δ，除了可由故障前数据根据式（3）计算得出，对于LG以及LL故障，也可由故障后数据估计出来［17］。对于LG故障，有：

线路正序、负序特性阻抗、传播常数相等，因此由式（17）、（29）可得不同步角 δ：

对于LL故障，有：

因此有：

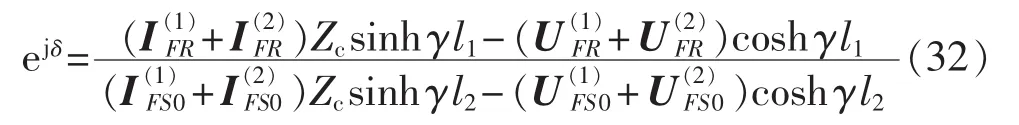
上述方法与并联电抗器模型无关，也适用于其他并联补偿装置。但是该方法假设过渡电阻呈现纯电阻性，并且需要故障类型，对于LG故障还需要利用线路零序参数。因此，所提的基于并联电抗器等值阻抗估计的故障定位算法与无需并联电抗器模型的故障定位算法各有优劣，实际中可根据情况选取。

3 算例

3.1 仿真模型

在PSCAD/EMTDC中建立如图3所示的500 kV测试系统，线路全长350 km，线路两端及中间安装有并联电抗器，系统相关参数参见文献［5］，故障定位算法基于MATLAB实现。相关电压、电流相量值通过对PSCAD/EMTDC仿真平台测量值进行离散傅立叶变换 DFT（Discrete Fourier Transform）求得，采样频率为4 kHz。线路两端的并联电抗器测量电流引入线路测量电流中进行补偿，故障定位只考虑线路中间的并联电抗器。在PSCAD/EMTDC得到的两侧电压、电流相量同步，因此为了评估非同步数据对故障定位的影响，将两侧相量数据人为设置不同步角δ［7］。

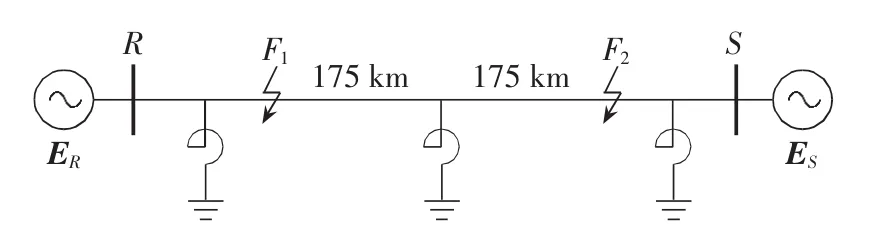
图3 仿真模型Fig.3 Simulation model

3.2 典型故障定位结果

定义故障定位误差百分比为：

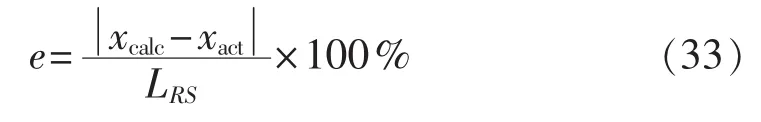
其中，xact为实际故障距离；xcalc为故障距离计算值；LRS为线路全长350 km。以线路RS左侧F1处故障为例。F1距离R端母线160 km，过渡电阻为10 Ω，设两端数据不同步角δ为10°，定位结果精确到1 m。采用基于并联电抗器等值阻抗估计的故障定位算法求得故障距离为160.154 km，定位误差为0.0440%。采用无需并联电抗器模型的故障定位算法求得故障距离为160.082 km，该方法对于双端数据不同步的补偿采用故障后的数据。图4列出了故障定位函数在定位区间的变化示意图。可见，定位函数在区间（0，175）km 以及（175，350）km 内呈单调变化，在区间（0，175）km内有根，定位结果误差为0.0234%。

图4 故障定位函数示意图Fig.4 Schematic diagram of fault location function

3.3 不同故障条件影响

为了评估本文方案在不同故障条件下的有效性，设置不同故障点位置、不同故障类型、不同过渡电阻的线路故障，部分仿真结果见表2、表3。表中，仿真设置的故障类型包括：单相接地故障（AG）、两相接地故障（BCG）、两相相间故障（BC）和三相故障（ABC）。表中，故障距离为故障点与母线R的距离，后同；M1表示基于并联电抗器等值阻抗估计的故障定位算法，M2表示无需并联电抗器模型的故障定位算法；Rf为过渡电阻；双端数据不同步角δ均设为10°。

由仿真结果可见，所提的故障定位算法在各种故障条件下均能够精确地得到故障点位置。由表2的定位结果误差可知，不同的故障类型对2种方法的线路故障定位结果影响很小，但值得一提的是，M2需要知道故障类型。由表3的定位结果误差可知，过渡电阻的增加将导致M1的定位误差稍微增大，但定位结果仍具有很高的精度，而M2则几乎不受过渡电阻的影响。因此，可认为所提方法对故障点位置、故障类型及过渡电阻均不敏感。

表2 不同故障类型下的故障定位结果Table 2 Results of fault location for different fault types

表3 不同过渡电阻下的故障定位结果Table 3 Results of fault location for different fault resistances

3.4 双端数据不同步角的影响

为了评估本文方案在双端数据不同步角下的有效性，设置了不同的δ值，表4列出了部分仿真结果。表4中的故障条件为A相接地故障，过渡电阻为10 Ω。分别采用故障前数据及故障后数据对δ进行估计，即故障前数据采用式（3）进行计算，故障后数据采用式（30）进行计算。M1采用故障前数据计算的δ值，M2采用故障后数据计算的δ值。由表可见，所提方法均能比较准确地进行数据不同步的补偿，定位结果误差不受双端数据不同步角的影响。

3.5 相量测量误差的影响

所提算法中需要的工频量及电压、电流测量值必须经过电压互感器、电流互感器的变换，考虑测量结果可能存在一定的误差，表5列出了电压、电流相量不同程度的测量误差对故障定位结果精度的影响情况，其中故障点距离母线R 150 km，过渡电阻为10 Ω。由表5可见，相量测量误差对故障定位结果的准确性有一定影响，其中M1受影响较小，M2则受影响较大。当测量误差最大达到5%时，M1的误差最大为0.3151%，而M2的误差最大可达2.2651%。同时由表5可知，相量测量误差导致的故障定位结果误差与故障类型无关。

表4 数据不同步角对故障定位结果的影响Table 4 Impact of data asynchronization angle on fault location

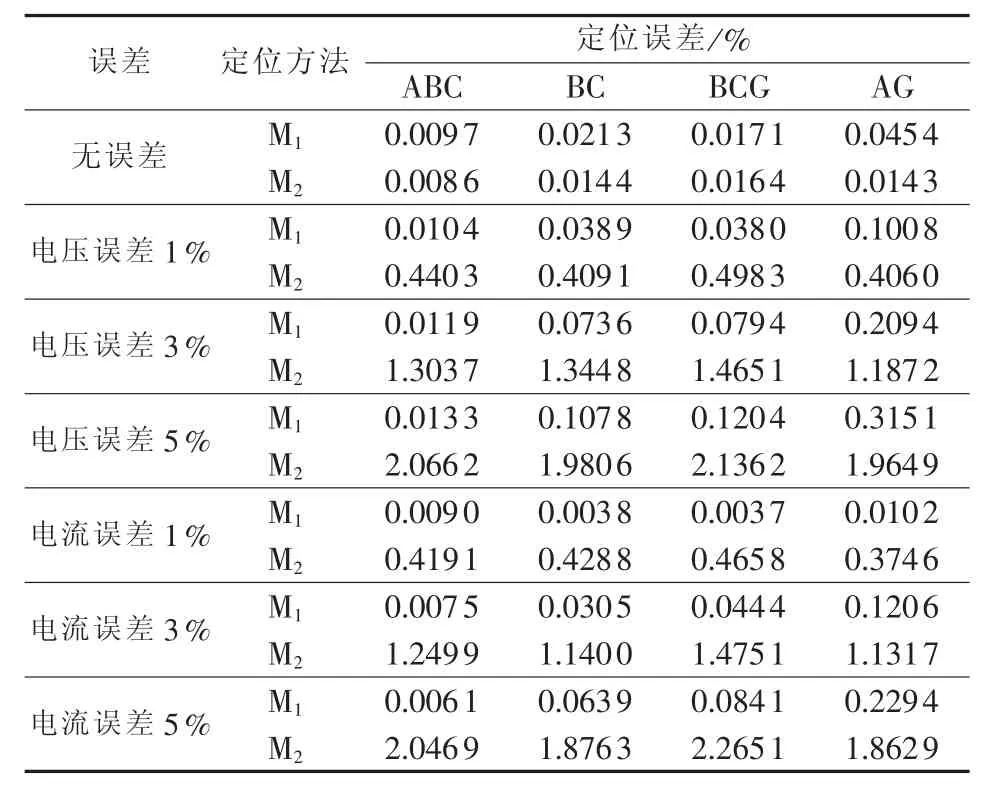
表5 相量测量误差对故障定位结果的影响Table 5 Impact of measurement error on fault location

3.6 线路参数误差的影响

本文所提的故障定位算法需要线路参数，表6列出了线路参数误差对故障定位精度影响的部分结果。其中故障点距离母线R 300 km，过渡电阻为10 Ω。由表6可见，线路参数的误差对故障定位结果的精度有一定影响，M1相对M2而言，受线路参数误差影响更小。单相接地故障与两相相间故障和两相接地故障相比，所提方法在发生单相接地故障时受线路参数误差影响更小。当线路误差最大达到5%时，M1的误差最大为0.7411%，而M2的误差最大可达1.3219%。

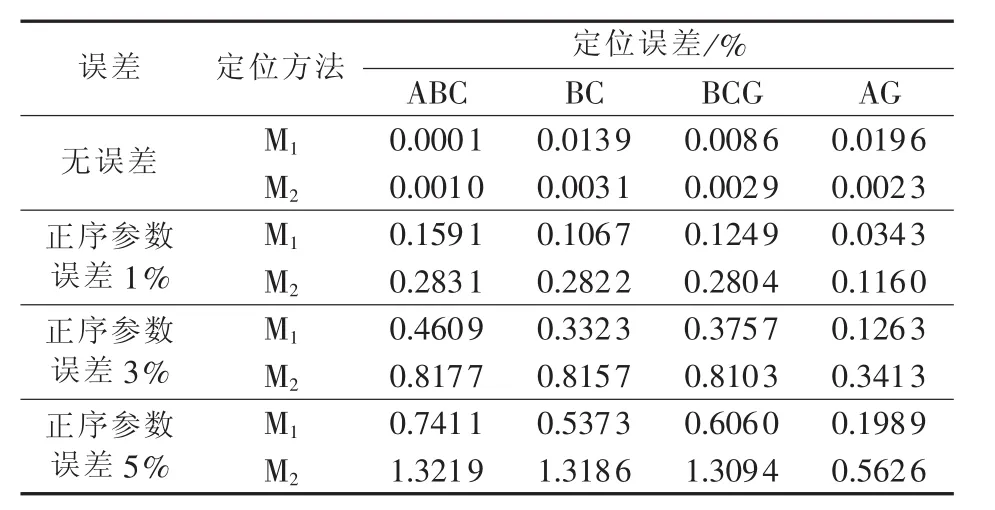
表6 线路参数误差对故障定位结果的影响Table6 Impact of line parameter error on fault location

4 结论

本文针对长距离输电线路中间带并联电抗器的故障定位提出了2种双端故障定位算法。其中，基于并联电抗器等值阻抗估计的故障定位算法只需正序参数，无需故障类型，测距结果稳定，但该方法需要故障前数据，且假设故障前后并联电抗器等值阻抗不变。而无需并联电抗器模型的故障定位算法则与并联电抗器无关，也适用于其他并联补偿设备，但该方法需要故障类型，且在进行单相接地故障定位时还需要线路零序参数。同时，针对可能出现的双端数据不同步的情况本文还研究了相应的补偿方法。大量仿真结果表明了所提方法对各种故障均有较好的适用性。实际中，可根据运行条件选取相应的故障定位方法。

［1］张健康，粟小华，胡勇，等.大容量可控电抗器对线路差动保护的影响及解决措施［J］.电力系统自动化，2014，38（1）：115-120.ZHANG Jiankang，SU Xiaohua，HU Yong，et al.Impact of largecapacity controllable shunt reactor on line differential protection and solutions［J］.Automation of Electric Power Systems，2014，38（1）：115-120.

［2］商立群，陈琦.特高压输电线路并联电抗器补偿方案［J］.中国电力，2015，48（4）：95-100.SHANG Liqun，CHEN Qi.Research on three-phase shunt reactor compensation of UHV transmission lines［J］.Electric Power，2015，48（4）：95-100.

［3］GHAZIZADEH-AHSAEE M，SADEH J.Accurate fault location algorithm for transmission lines in the presence of shunt-connected flexible AC transmission system devices［J］.IET Generation，Transmission&Distribution，2012，6（3）：247-255.

［4］林富洪.超高压带并联电抗器线路的故障测距算法［J］.现代电力，2010，27（1）：40-44.LIN Fuhong.Novel fault location algorithm for EHV transmission line with shunt reactor［J］.Modern Electric Power，2010，27（1）：40-44.

［5］郭容，刘新东，曾锐明.带并联电抗器高压长线路的故障测距算法研究［J］.现代电力，2013，30（4）：62-66.GUO Rong，LIU Xindong，ZENG Ruiming.Research on fault location algorithm for EHV long transmission line with shunt reactors［J］.Modern Electric Power，2013，30（4）：62-66.

［6］HUSSAIN S，OSMAN A H.Fault location on series and shunt compensated lines using unsynchronized measurements［J］.Electric Power Systems Research，2014，116（116）：166-173.

［7］夏经德，张向聪，黄新波，等.基于纵向阻抗的双端量故障测距新算法［J］.电力自动化设备，2015，35（10）：133-139.XIA Jingde，ZHANG Xiangcong，HUANG Xinbo，etal.Fault locating based on longitudinal impedance according to dualterminal variables［J］.Electric Power Automation Equipment，2015，35（10）：133-139.

［8］刘东超，李永丽，曾治安.带并联电抗器的双回线故障测距算法研究［J］.电力系统及其自动化学报，2006，18（2）：5-9.LIU Dongchao，LI Yongli，ZENG Zhian.Research on accurate fault location algorithm for double circuit transmission line with shunt reactors［J］.Proceedings of the CSU-EPSA，2006，18（2）：5-9.

［9］张丽，徐玉琴.并联电抗器在超（特）高压电网中应用及发展［J］.电力自动化设备，2007，27（4）：75-78.ZHANG Li，XU Yuqin.Application and development of shunt reactors in EHV&UHV transmission lines［J］.Electric Power Automation Equipment，2007，27（4）：75-78.

［10］廖敏，昃萌.分级可控并联电抗器的控制策略及保护配置［J］.电力系统自动化，2010，34（15）：56-59.LIAO Min，ZE Meng.Control strategy and protection configuration for step controlled shunt reactor［J］.Automation of Electric Power Systems，2010，34（15）：56-59.

［11］高厚磊，陈学伟，刘洪正，等.基于改进参数检测法的双端非同步数据故障测距算法［J］.电力自动化设备，2014，34（9）：27-32.GAO Houlei，CHEN Xuewei，LIU Hongzheng，et al.Two-terminal asynchronous data fault location algorithm based on improved parameter detection method［J］.Electric Power Automation Equipment，2014，34（9）：27-32.

［12］IZYKOWSKI J，ROSOLOWSKI E，BALCEREK P，et al.Accurate noniterative fault location algorithm utilizing two-end unsynchronized measurements［J］.IEEE Transactions on Power Delivery，2010，26（1）：72-80.

［13］YU C S.An unsynchronized measurements correction method for two-terminal fault-location problems［J］.IEEE Transactions on Power Delivery，2010，25（3）：1325-1333.

［14］陈旭，朱永利，郭小红，等.基于相位特性的高压输电线路双端非同步故障测距算法［J］.电力系统自动化，2015，39（22）：152-156.CHEN Xu，ZHU Yongli，GUO Xiaohong，et al.A two terminal faultlocation algorithm using asynchronousdata based on phase characteristics for high voltage transmission line［J］.Automation of Electric Power Systems，2015，39（22）：152-156.

［15］桂勋，刘志刚，韩旭东，等.基于高压输电线电压沿线分布规律的故障双端测距算法［J］.中国电机工程学报，2009，29（19）：63-69.GUI Xun，LIU Zhigang，HAN Xudong，et al.An accurate algorithm of two-terminal fault location based on the distribution of line voltage along HV transmission line［J］.Proceedings of the CSEE，2009，29（19）：63-69.

［16］JIANG Z，MIAO S H，XU H，et al.An effective fault location technique fortransmission grids using phasormeasurement units［J］.International Journal of Electrical Power& Energy Systems，2012，42（1）：653-660.

［17］IZYKOWSKI J，ROSOLOWSKI E，BALCEREK P，et al.Fault location on double-circuit series-compensated lines using twoend unsynchronized measurements［J］.IEEE Transactions on Power Delivery，2011，26（4）：2072-2080.