考虑光伏不确定性的安全约束机组组合

李秋燕 ，王利利，丁 岩 ，关朝杰，胡 钋 ，汪原浩

（1.国网河南省电力公司经济技术研究院，河南 郑州 450000；2.武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

目前，世界各地都在开展大容量光伏并网工作。相比于传统火力、水力发电等常规发电方式，光伏发电最显著的特点是其出力具有间歇性、波动性和随机性［1-5］，这使得光伏电站通常被当作系统的扰动源，假设光伏并网系统的发电量能够全部被所在负荷点吸收，在实际系统中光伏出力作为负的负荷，与原负荷进行线性组合形成等效负荷［6］，通过这种方式获取的不确定性负荷并不是电网的实际负荷［7］，这势必会影响系统中传统旋转机组的优化调度，因此必须配合常规电源，以确保电能可以安全稳定地输送到用户端。然而，大量的光伏并网使得总负荷减少，若机组不改变原有的启停计划，可能造成线路有功功率越限。另一方面，在机组组合中引入光伏发电系统，可为系统运行节省燃料成本，减少能源消耗及温室气体排放，缓解环境污染。为保证光伏并网后能充分调动电网的输电能力，实现电网经济性与安全性的和谐统一，需要重点研究大容量光伏并网与电网安全约束机组组合SCUC（Security-Constrained Unit Commitment）的问题。

国内外关于求解机组组合的方法很多。文献［8］给出了一种优先级表的计算方法；文献［9］提出了一种基于粒子群优化算法解决电力系统机组组合问题的智能算法；文献［10］应用拉格朗日松弛法来解决机组组合问题。然而，所有这些方法都只考虑了发电与负荷的功率平衡、旋转备用等基本约束，并未提出计及负荷及光伏预测误差不确定性的机组组合方法。因此，本文在混合整数规划MIP（Mixed IntegerProgramming）法［11］的 研 究 基 础 之 上 ，利 用Benders分解算法在安全约束组合优化中的割集分解思想，以区间量的形式描述负荷及光伏发电预测值，提出了一种求解计及负荷和光伏出力不确定性的SCUC模型的方法，最后通过算例分析了系统加入光伏前后的经济效益变化以及不同指标下的总运行费用。

1 系统的不确定性模型

1.1 负荷的不确定性模型

目前，在短期负荷预测的应用领域中已有很多成熟的理论［12］。 其中，文献［13］给出了一种能够精确预测短期负荷的方法，即假定事先可以获取以τ为时间间隔的Γ周期内的负荷预测值，并将实际负荷的不确定性表示为一个具有零均值、呈正态分布的预测误差即总体服从期望为μ1=0、标准差为σ1的正态分布，则实际负荷可近似表示为：

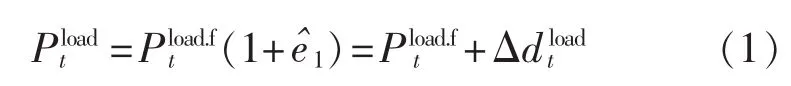
其中为t时刻实际负荷值为t时刻事先获取的负荷预测值为t时刻不确定的负荷预测误差。

1.2 光伏出力的不确定性模型

电力系统中光伏电源作为一种扰动源，其出力的波动性和不确定性是很难被预知的，可以采用与负荷预测建模相同的方法对光伏出力预测进行建模，将实际光伏出力的不确定性表示为一个具有零均值、呈正态分布的预测误差即总体服从期望为μ2=0、标准差为σ2的正态分布，则实际光伏出力可近似表示为：

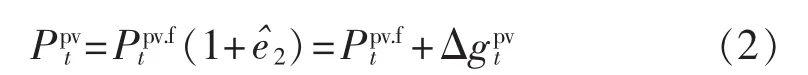
其中为t时刻实际光伏出力值为t时刻事先获取的光伏预测值为t时刻不确定的光伏出力预测误差。

2 基于预测误差的SCUC模型

2.1 目标函数

在只考虑系统中火电机组及光伏电站的运行成本的情况下，将光伏电站被全额消纳的出力作为“负的负荷”与原负荷进行线性组合，就形成了所谓的“等效负荷”。因此，含光伏并网发电系统的目标函数为火电机组的煤耗费用及启停费用最小，即：

其中，Ui，t为机组 i在 t时刻的运行状态，开机时取1，停机时取 0；T 为时间常数；Ng为机组数；Pi，t为机组 i在 t时刻的有功出力值；ai、bi、ci为机组 i的煤耗量特性常数；αi为机组i的启动和维护费用；βi为机组i在冷却环境下的启动费用；τi为机组i的冷却速度时间常数为机组i截止到t时刻连续停机的时间。

2.2 约束条件

由于负荷及光伏出力预测误差的随机性，所以约束条件中存在不确定性变量。因此，本文采用区间估计法［15］将负荷及光伏出力的不确定性表示为区间量的形式，允许所做决策在一定程度上不满足约束条件，而采用置信度控制这种不满足约束的风险，兼顾了风险和成本。根据区间估计理论，在样本方差已知的情况下，可以获得样本均值X在置信度为1-α下的置信区间为：

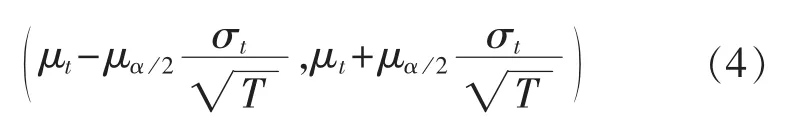
其中，α为不确定性变量的期望显著性水平；μt为t时刻不确定性变量的期望；μα/2为α/2时刻不确定性变量的期望；σt为t时刻不确定性变量的标准差。

因此，含有不确定参变量的发电与负荷功率平衡以及系统旋转备用容量的约束条件可表示为：

其中分别为 t时刻根据预测获得的负荷及光伏出力的区间量和分别为 t时刻系统负荷的最大值与最小值分别为t时刻光伏出力最大值与最小值。每一时刻都对应一种场景，若干时刻就会出现无数种场景，事实上，以下3种极限场景即可满足描述问题的需要：式（5）中负荷取最大值，光伏出力取平均值；式（6）中负荷取最大值，光伏出力取最小值；再补充一个负旋转备用容量约束式使得机组的最小出力能够满足光伏出力最大时的系统平衡需求。这三者就可以确保满足极端情况下的机组出力要求，即：

其中分别为机组i的最大和最小技术出力；Rt为t时刻系统的旋转备用容量，取负荷的5%，单位为MW。

常规约束条件包括机组有功功率技术出力、机组输出有功功率调整率、机组的最小启停时间，即：

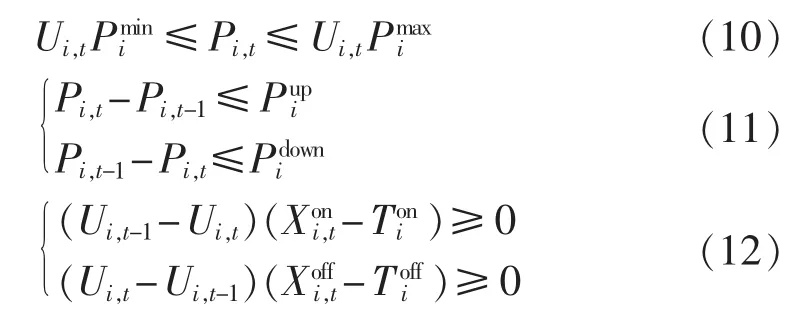
其中分别为机组 i的最小启动时间和最小停运时间分别为机组i的启动所需时间和停机所需时间为机组i的最大爬荷速率，为机组i的最大卸荷速率，单位为MW/h。

静态网络安全约束可以采用发电机输出功率转移分布因子（GSDF）将其线性化表示为：

其中，M为节点数为节点j对线路l的功率转移分布因子；Pj，t为节点j在t时刻的净注入功率；为线路传输功率最大值。

3 模型求解的Benders分解算法

3.1 算法优化机制

为了便于描述Benders分解算法的优化机制，将原问题抽象表达为如下形式［14］：

其中，b 和 h 为常数；min f（x）为目标函数，m 维整型变量x表示机组启停状态变量，即输出的有功功率；m维连续变量y表示复杂变量；e为定义在Rm×Rm的m×m维矢量函数。Benders分解包括以下步骤。

步骤1：将原问题进行降维处理，即不考虑原问题中的约束式（16），得到线性优化问题模型，如式（17）所示。

求解此模型即可得到优化结果。

步骤2：为了检验步骤1中的优化结果是否满足不等式约束式（16），引入非负的松弛变量向量s，形成优化问题模型的从决策，如式（18）所示。

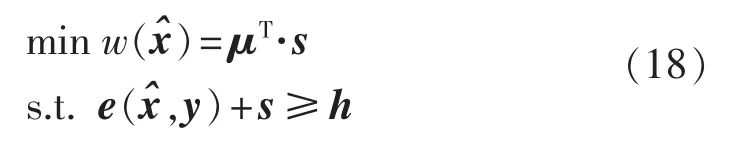
其中，μ为与松弛变量具有相同维度的单位向量。

步骤3：在从决策中引入松弛变量s的作用是当给定的优化结果不满足约束条件式（16）时，用该变量来暂时缓解这一情况，以确保步骤2中的优化问题模型有解。式（17）、（19）构成了原问题的主决策。 当式（18）表示的目标函数时，利用主决策获得的优化结果不可行。因此，主决策在下次迭代中需要向式（17）补充Benders割，以对优化结果进行修正，补充的Benders割可以表示为：

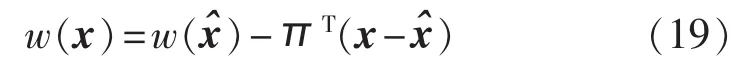
其中，π为从决策获得最优解时x相对于目标函数值的灵敏度。这样，通过对主从决策的交替求解，最终可以获得满足约束式（15）、（16）的优化结果。

步骤4：设置收敛条件，即在主从决策进行n次迭代过程中，当从决策松弛变量s=0时，满足则算法结束。 ε 为预先设定第k次迭代与第k+1次迭代所得优化结果的偏差。

Benders分解算法流程如图1所示。

图1 Benders分解算法流程图Fig.1 Flowchart of Benders decomposition algorithm

3.2 SCUC的求解

本文所要解决的问题属于混合整数规划问题，直接求解较为复杂，因此基于Benders算法的优化机制，将SCUC问题分解为一对相互制约的主问题MP（Master Problem）和子问题 SP（Sub-Problem），这样可极大地简化求解过程，并且可以调用具有多种优化算法的CPLEX软件，寻求全局最优解。

主问题是不考虑网络安全约束式的机组组合问题，子问题则是机组启停状态完全确定情况下对各支路有功功率是否越限的检测问题，可描述为：

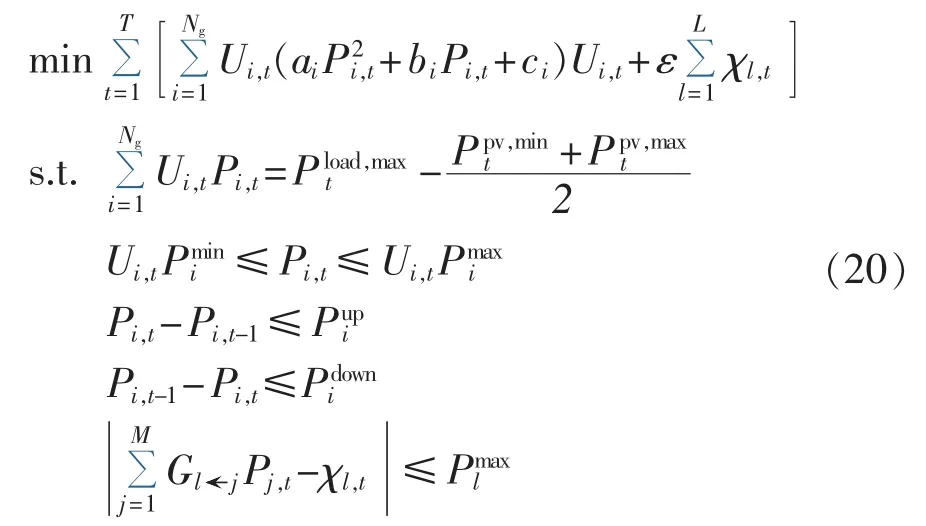
其中，L为线路总数量；虚拟变量 χl，t为反映线路l上的传输功率对机组启停状态的制约程度。检测问题模型的目标函数和约束条件都是线性的，可以采用文献［15］的方法求解。在主问题优化开始时，应对不可行的机组组合方案进行修正，以消除虚拟变量，从而可进一步消除线路有功功率越限的情况，达到静态网络安全约束的要求。根据直流潮流约束的表达方式，采用表示第l条传输线路在t时刻机组启停状态变量与虚拟变量之间的牵制关系，作为消除虚拟变量的衡量标准。显然，若能够修正机组启停方案使则可以消除线路有功功率越限。主问题应该补充的Benders割为：

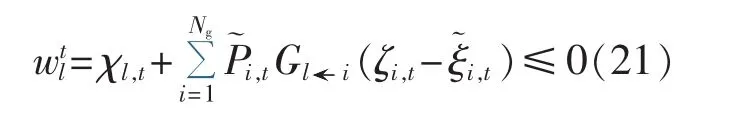
其中为主问题的解为子问题机组的有功功率输出，对子问题中停运的机组以代替；ζi，t为当前决策量。

4 算例及分析

Benders算法流程图见图2。应用MATLAB和CPLEX，在内存为 4 G，主频为 2.2 GHz的双核 PC机上对系统进行建模。如图3所示加入了光伏的WSCC 9节点、3机组系统，母线7处安装额定功率为50 MW的光伏发电机组。机组数据、机组运行参数及线路参数参照文献［16］，该系统最大负荷功率为259 MW。

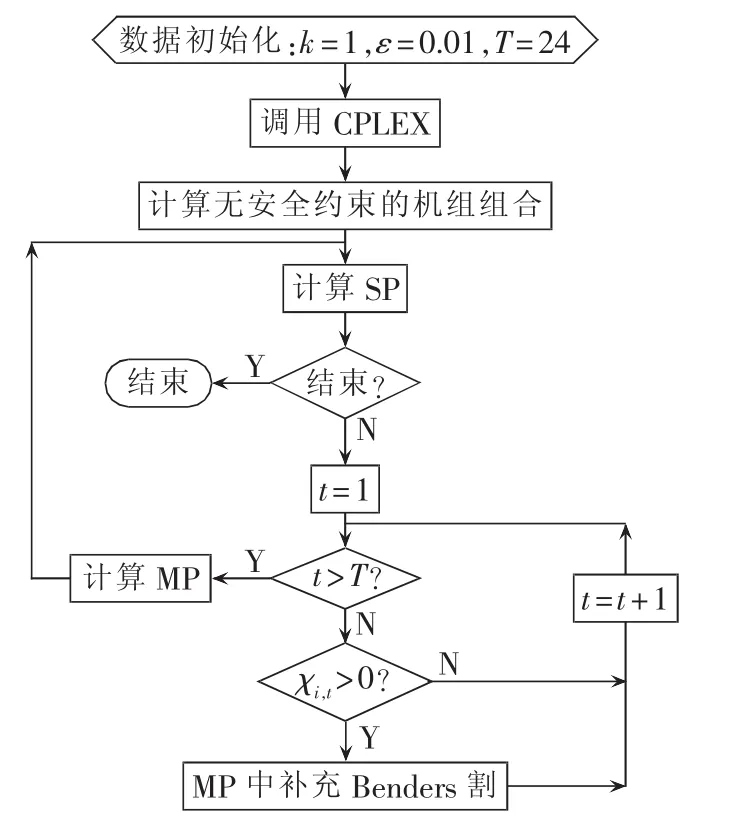
图2 算法流程图Fig.2 Flowchart of algorithm

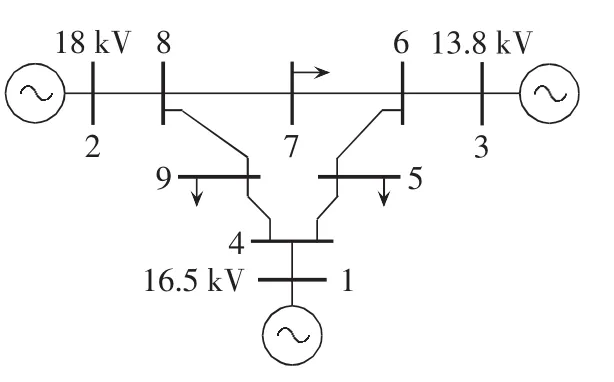
图3 WSCC 9节点系统接线图Fig.3 WSCC 9-bus system

如图 4（a）、（b）所示为负荷及光伏出力区间量表示（图中负荷率、光伏出力率为标幺值），其预测负荷误差的标准差为 σload=0.05 p.u.［8］、σpv=0.10 p.u.［17］，据此可以计算得到各时段系统负荷及光伏出力区间量，分别如表1、2所示。

图4 负荷及光伏出力区间量表示Fig.4 Intervals of load and PV output

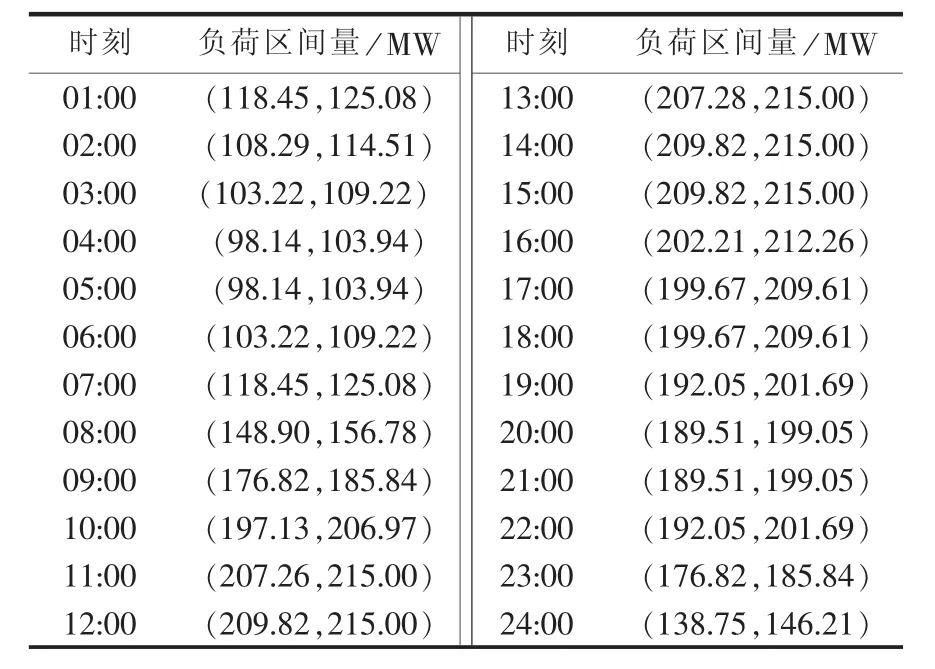
表1 负荷区间量Table 1 Intervals of load

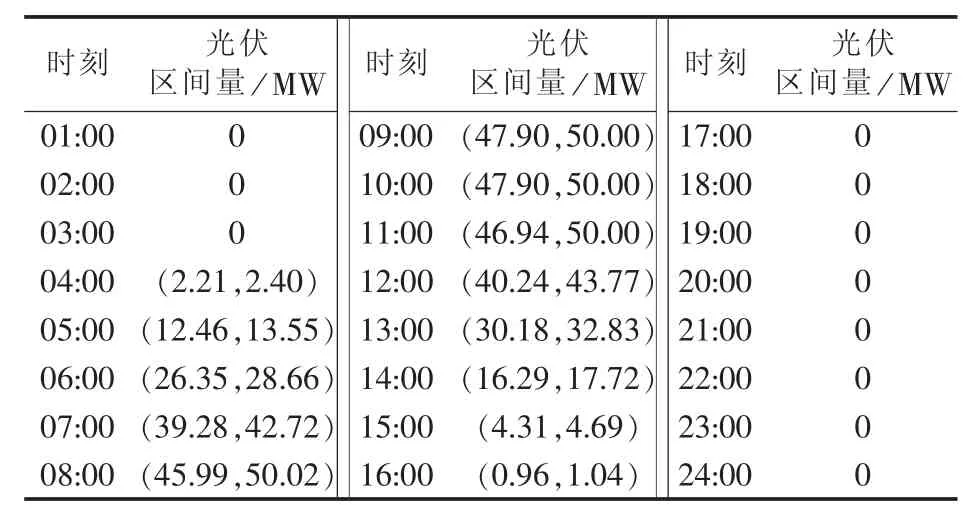
表2 光伏出力数据Table 2 Intervals of PV output

针对以上数据进行计算，图5所示为WSCC 9节点系统在计及电网安全约束和预测误差不确定性的机组启停方案，可以看出系统中的3台机组在每个时段都全部开机，各机组的出力情况如表3所示，此时系统总的运行成本为$94558.2。

图5 机组启停方案Fig.5 Unit startup-shutdown scheme

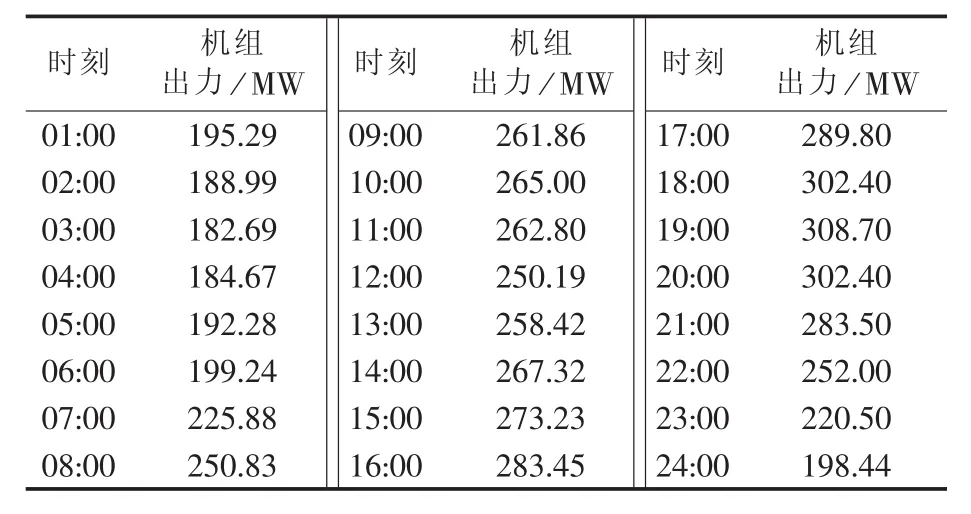
表3 机组出力Table 3 Unit outputs

针对以上数据，表4反映了2种运行指标下系统总运行费用的差异，若不计光伏电站的建设成本，光伏并网下SCUC问题的总运行费用为$94558.2，而无光伏并网的SCUC总运行费用为$117092.7，这说明光伏并网后使整个电网系统总的煤耗费用降低，即光伏电站的发电功率承担了系统的一部分负荷。

如图6所示为在样本数量为24 h，且预测误差标准差 σload=0.05 p.u.、σpv=0.10 p.u.时，不同置信区间下机组组合总运行费用的变化趋势，可见随着置信度的增大，置信区间的精度逐渐降低，负荷及光伏出力区间量范围扩大，等效负荷需求量增加，因此提高了总发电，增加了运行费用。

表4 运行成本Table 4 Operational costs

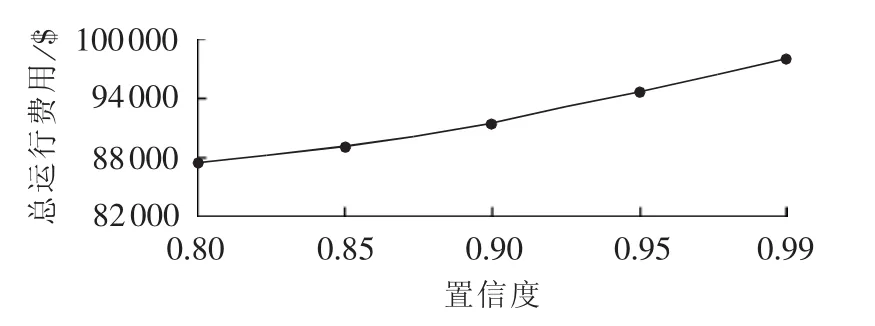
图6 不同置信度下SCUC运行费用Fig.6 Curve of SCUC operational cost vs.confidence level

5 结论

本文基于传统SCUC问题的研究，引入了光伏发电并网系统，并用直流潮流约束进行求解。在考虑负荷及光伏出力时，采用区间量概念，并通过借用Benders算法在大规模混合整数规划问题中的灵活性和高效性，建立了光伏并网下考虑电网安全约束的机组组合模型，应用MATLAB和CPLEX对光伏并网后的WSCC 9节点系统进行了仿真分析，结果表明该机组组合模型可以在确保系统安全运行的情况下，可使其运行成本达到最低，具体结论如下。

（1）在安全问题上，光伏作为负的负荷加入系统会抵消一部分实际负荷，若此时不改变发电机组的启停方案可能会造成线路传输功率越限，利用本文所提出的方法可以重新确定光伏并网下的机组启停方案，消除线路有功功率越限情况，使系统恢复到原安全状态。

（2）在经济方面，光伏并网可减少部分火电机组的煤耗，使系统在光伏并网下的总体运行成本较无光伏并网下的大幅降低；而光伏并网下考虑网络安全约束后的总运行成本要比光伏并网下不考虑安全约束的又略有上升，这是因为考虑安全约束后会增加部分机组启停费用。

（3）在环保方面，光伏并网后大幅降低的煤耗，直接减少SO2、NO2等废气的排放。

［1］余涛.光伏发电并网关键技术及其对电网的影响研究［D］.上海：上海交通大学，2012.YU Tao.The study on the key technology and the impact on the grid of grid connected PV system［D］.Shanghai：Shanghai Jiao Tong University，2012.

［2］杨艳红，裴玮，邓卫，等.基于Benders分解的微电网联网运行优化［J］.电力自动化设备，2014，34（10）：21-27 YANG Yanhong，PEI Wei，DENG Wei，et al.Optimal operation of grid-connected microgrid based on Benders decomposition［J］.Electric Power Automation Equipment，2014，34（10）：21-27.

［3］BARKER P P，BING J M.Advance in solar photovoltaic technology：an application perspective［C］∥Power Engineering Society General Meeting.San Francisco，USA：IEEE，2005：1955-1960.

［4］强金龙，于尔铿.电力系统经济调度［M］.哈尔滨：哈尔滨工业大学出版社，1993：78-80.

［5］孙艳伟，王润，肖黎姗，等.中国并网光伏发电系统的经济性与环境效益［J］.中国人口 资源与环境，2011，21（4）：88-94.SUN Yanwei，WANG Run，XIAO Lishan，et al.Economical and environmental analysis of grid-connected photovoltaic systems in China［J］.China Population，Resources and Environment，2011，21（4）：88-94.

［6］汪洋，夏清，康重庆.机组组合算法中起作用整数变量的辨识方法［J］.中国电机工程学报，2010，30（13）：46-52.WANG Yang，XIA Qing，KANG Chongqing.Identification of the active integer variables in security constrained unit commitment［J］.Proceedings of the CSEE，2010，30（13）：46-52.

［7］张利，赵建国，韩学山.考虑网络安全约束的机组组合新算法［J］.电网技术，2006，30（21）：50-55.ZHANG Li，ZHAO Jianguo，HAN Xueshan. A new unit commitment algorithm considering network security constraints［J］.Power System Technology，2006，30（21）：50-55.

［8］BOUFFARD F，GALIANA F D.Stochastic security for operations planning with significant wind power generation［J］.IEEE Transactions on Power Systems，2008，23（2）：306-316.

［9］TOBIAS I，EL M A，LUQUE A.Colored solar cells with minimal current mismatch ［J］.IEEE Transactions on Electron Devices，1999，46（9）：1858-1865.

［10］胡家声，郭创新，曹一家.一种适合于电力系统机组组合问题的混合粒子群优化算法［J］.中国电机工程学报，2004，24（4）：24-28.HU Jiasheng，GUO Chuangxin，CAO Yijia.A hybrid particle swarm optimization method for unit commitment problem ［J］.Proceedings of the CSEE，2004，24（4）：24-28.

［11］夏清，钟海旺，康重庆.安全约束机组组合理论与应用的发展和展望［J］.中国电机工程学报，2013，33（16）：94-103.XIA Qing，ZHONG Haiwang，KANG Chongqing.Review and prospects of the security constrained unit commitment theory and applications［J］.Proceedings of the CSEE，2013，33（16）：94-103.

［12］茆美琴，龚文剑，张榴晨，等.基于EEMD-SVM方法的光伏电站短期出力预测［J］.中国电机工程学报，2013，33（34）：17-24.MAO Meiqin，GONG Wenjian，ZHANG Liuchen，et al.Shortterm photovoltaic generation forecasting based on EEMD-SVM combined method［J］.Proceedings of the CSEE，2013，33（34）：17-24.

［13］PENG X，JIRUTITIJAROEN P.A probabilistic unit commitment problem with photovoltaic generation system［C］∥TENCON 2009-2009 IEEE Region 10 Conference.Singapore：IEEE，2009：1-6.

［14］冯卫国.概率论与数理统计［M］.上海：上海交通大学出版社，2010：146-193.

［15］朱道立.大系统优化理论与应用［M］.上海：上海交通大学出版社，1987：112-125.

［16］WU Y C，DEBS A F，MARSTEN R E.A direct nonlinear predictor-corrector primal-dual interior point algorithm for optimal power flows［J］.IEEE Transactions on Power Systems，1994，9（2）：876-582.

［17］CHU M，NGUYEN H P.Photovoltaic station at MIT［EB/OL］.［2015-05-15］.http：∥pvbase.mit.edu/cgi-bin /index.py.