考虑双馈异步风电机组无功极限的静态电压稳定概率评估

鲍海波 ，韦 化 ，郭小璇

（1.广西大学 广西电力系统最优化与节能技术重点实验室，广西 南宁 530004；2.广西电网公司 南宁供电局，广西 南宁 530031）

0 引言

作为一种新型的可再生能源，风力发电对转变中国用能结构和供能结构、减小发电碳排放量有重要作用［1-2］。未来风电在电网所占比重越来越大，改变电力系统能源结构的同时，其随机性和间歇性也影响着系统的安全与稳定［3-19］。

关于含风电系统电压稳定性的研究［7-19］，国内外已有许多文献。文献［11-16］研究了风电系统电压稳定负荷裕度指标的概率评估问题，可以获取负荷裕度或临界功率的统计学分布，确定任意负荷水平系统发生静态电压失稳的概率。其模型将风电接入节点作为PQ节点，仅考虑了风电机组恒功率因数运行方式的简化模型。但当前主流的风电机组是双馈异步发电机 DFIG（Doubly-Fed Induction Generator），当其采取恒电压运行方式时具备一定的无功调压能力。DFIG风电机组在系统中所占比例逐渐增多，其将会成为一种有效的无功电源。显然，传统电压稳定概率分析模型假设DFIG风电机组仅以恒功率因数方式运行，忽略其无功调节作用，所得结果是有失准确的。

文献［17］根据微分代数方程系统的奇异诱导分岔理论，研究了DFIG风电机组发生暂态电压失稳的机理。文献［18］分析了DFIG风电机组采用恒功率因数和恒电压2种运行方式对系统静态和中长期电压稳定性的影响，但所研究的风电机组模型没有考虑网侧变换器GSC（Grid Side Converter）注入的无功功率。文献［19］研究了考虑DFIG风电机组和网侧变换器的无功功率的长期电压稳定问题，没有涉及风速随机特性和相关性对电压稳定影响的分析。

本文考虑了DFIG风电机组恒电压运行的无功极限，构建了更为合理的静态电压稳定概率分析模型，并采用蒙特卡罗法结合内点法加以求解。将DFIG风电机组接入节点作为PV节点引入静态电压稳定概率评估模型，考虑了DFIG风电机组和网侧变换器的注入无功功率，分析了风速随机性和相关性对风电机组注入无功功率和系统电压稳定性的影响。IEEE 118和300节点标准系统的计算结果表明，所提模型和方法能更深层次挖掘风电机组电压支撑能力，对电力系统的电压稳定性分析更为准确，有利于系统的安全稳定运行。

1 DFIG风电机组的无功极限

图1是DFIG风电机组基本结构图［20-22］，定子直接经变压器接入电网，转子与反馈回路的机侧变换器和网侧变换器相连。DFIG风电机组采取恒功率因数方式运行时，可将其作为PQ节点；采用恒电压运行方式时，其具备一定的无功调压能力，可作为PV节点处理。图1中，Pm为风电机组的吸收功率，Ps和Qs分别为定子的注入有功和无功功率，Pw和Qw分别为DFIG风电机组注入电网的有功和无功功率，Pg和Qg分别为网侧变换器的注入有功和无功功率。

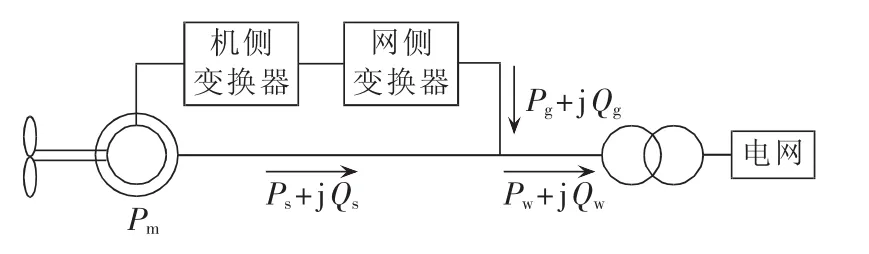
图1 DFIG风电机组的结构图Fig.1 Configuration of DFIG

风电机组不同风速条件下通过调节桨距调整有功功率，那么风电机组输出有功为：

其中，v 为风速；vin为切入风速；vout为切出风速；vr为额定风速；Pr为风电机组的额定输出功率；Pw为风电机组实际输出功率；a=Prvin/（vin-vr）和 b=Pr/（vinvr）为常数。其中风机有功功率由风速决定，风速一般服从分布形状参数为K、尺度参数为C的双参数威布尔（Weibull）分布。

DFIG风电机组输出的无功功率为：

以往的研究忽略了网侧变换器的注入功率，将式（2）近似为Qw=Qs。风电机组的无功功率则由定子注入无功功率 Qs和网侧变换器注入无功Qg决定。定子注入无功Qs需要满足最大转子电流的约束限制［21-22］：

其中，Ir为最大转子电流；Us为定子电压，即风电机组机端电压；Xm和Xs分别为励磁电抗和转子电抗；s为机组滑差。同时Qs也需要满足定子绕组温升限制，即最大定子电流的约束限制［21-22］：

其中，Is为最大定子电流。

网侧变换器的无功注入Qg需满足变换器的容量约束限制［19］：

其中，Sg为网侧变换器的容量。

根据式（2），整理出DFIG风电机组无功功率限制为：

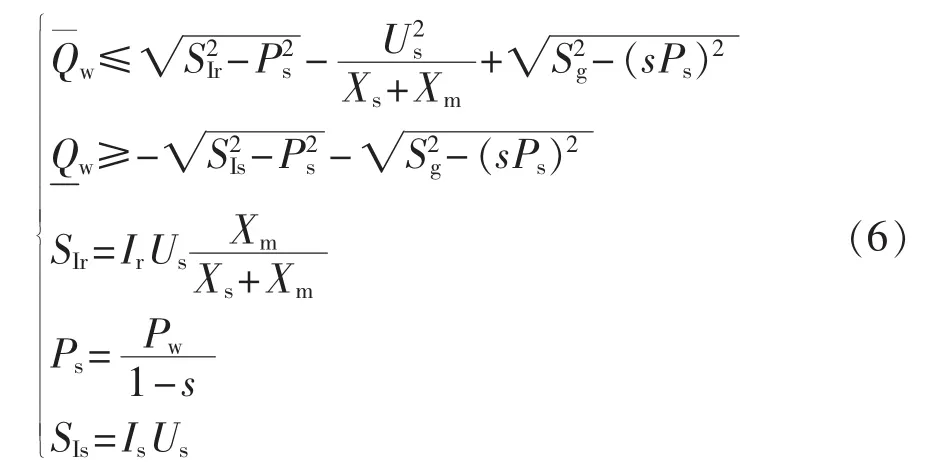
其中分别为DFIG风电机组输出无功功率的上、下边界。

图2是式（6）所表达的DFIG风电机组恒电压运行的安全运行区域。不考虑网侧变换器时，其无功输出边界是由DFIG风电机组的最大定子电流、最大转子电流等限制决定，Qw=Qs；考虑网侧变换器后其无功输出边界由风机和网侧变换器共同决定，Qw=Qs+Qg，上下边界均有所增大。

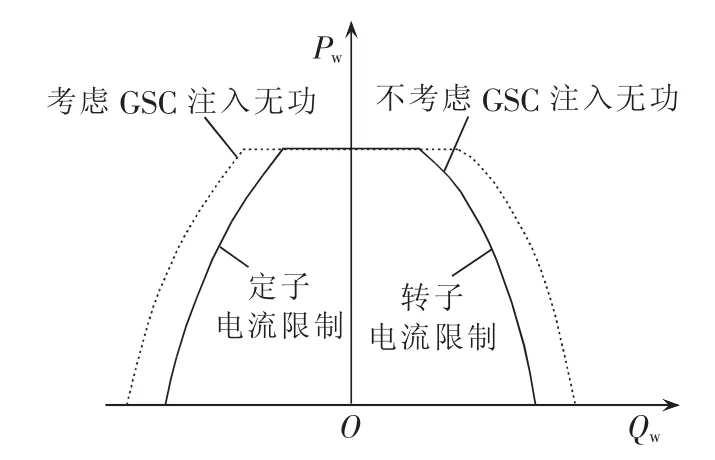
图2 DFIG风电机组运行极限图Fig.2 Operating limits of DFIG

2 考虑风电机组无功极限的电压稳定概率评估

风电场的各台风电机组处于同一个风速带，其运行模式通常保持一致，故本文假设风电场内各台风电机组均以同一方式运行，风电场出力等于各台机组出力之和。负荷裕度表征的是系统当前运行点到电压稳定临界点的距离，研究负荷裕度指标是研究电力系统静态电压稳定性的有效手段。以负荷裕度指标最大化为优化目标，将本文DFIG风电机组输出无功功率模型式（6），引入电压稳定概率评估模型，具体如下。

a.目标函数：

b.约束条件：

其中，SB为系统所有节点集合；SG为发电机节点集合；SR为无功电源节点集合；系统无功电源QRi具体包括系统的常规发电机、电容器、SVC、SVG等设备；SL为未接发电机和风电机组的节点集合；λ为负荷增加的参数标量，即负荷裕度；bPi和bQi为节点i的负荷增加方向；临界功率Pc为系统电压稳定临界点处电力网络的输送功率，根据潮流方程式（8），其与负荷裕度的关系为和 δi分别为节点i的电压幅值和相角；Yij为节点导纳矩阵元素；αij为节点导纳矩阵相应元素的相角；δij=δi-δj-αij；Ni为节点 i的风电场风电机组数量分别为节点i的电压幅值上、下限；Usi和URi分别为风电场和常规发电机的机端电压，本文不考虑PV/PQ节点的转换，其值均为常数。

式（7）—（20）电压稳定指标计算是基于最优化模型，将系统潮流方程作为等式约束条件，最终求解结果满足此等式约束，确保发电机功率满足系统的负荷平衡。式（7）—（20）的电压稳定概率评估模型是典型的非线性规划问题，若需考虑常规发电机功率圆图特性等更为复杂的运行限制［23］，只需将相关约束条件耦合到模型即可。若需考虑风电机组PV/PQ转换逻辑，可参考文献［23］将其表达为互补约束引入模型求解。

为了精确分析风速的随机特性对风电场无功调节能力和整个系统电压稳定的影响，尽可能减小算法误差对结果分析的影响，本文采用蒙特卡罗法［24］结合现代内点法［25-26］对式（7）—（20）的概率分析问题进行求解。本文研究的是风速随机性和相关性对电压稳定性的影响，采用了Weibull分布和相关系数表达风速的随机性和相关性，存在一定简化，但应用于本文研究是可以接受的。同时，所提模型和方法具有很好的适应性，其他类型或不规则的风速随机性和相关性模型，也可直接耦合所提模型进行分析。

3 模型求解

3.1 相关变量处理

风电场的集中建设导致风电场之间风速存在一定的相关性。满足Weibull分布且具有相关性的风速采样点，无法通过蒙特卡罗法直接获得，参考文献［27］对相关随机变量进行如下两步处理：（1）蒙特卡罗抽样获得标准正态分布的采样点，并利用正交变换将该采样点转换为相关的标准正态分布采样点；（2）通过边际转换技术［27］，将相关的标准正态分布采样点等概率变换为相关的Weibull分布采样点。

将风速表达为随机向量 X=［x1，x2，…，xn］T，均值μX=［μ1，μ2，…，μn］T，方差 σX=［σ1，σ2，…，σn］T，随机变量xi和xj之间相关系数为ρij，其表达的是xi和xj之间的线性相关关系，定义为其中Cov（·）和D（·）分别为随机变量协方差和方差运算符。风电场风速的相关系数矩阵为：

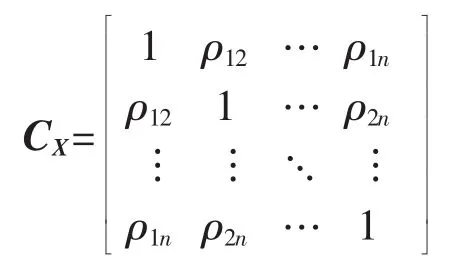
利用边际转换，随机向量X与相关系数矩阵为CY的标准正态分布随机向量 Y=［y1，y2，…，yn］T等概率变换关系为［27］：

其中，Hxi（xi）为输入变量 xi的累积概率分布函数；Φ（·）为标准正态分布的累积概率分布函数。CY为：

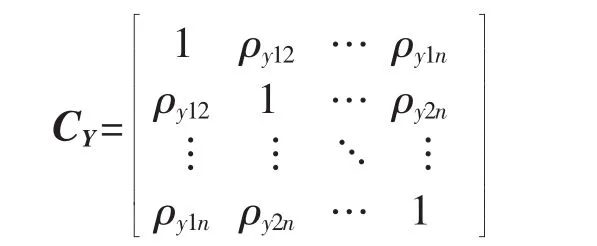
CY与 CX元素之间的关系为［27］：

其中，G（·）为以ρij为自变量的函数，其具体计算与相关的随机变量xi和xj的具体概率分布类型有关。根据经验公式，若随机变量xi和xj均服从Weibull分布，可近似得到：

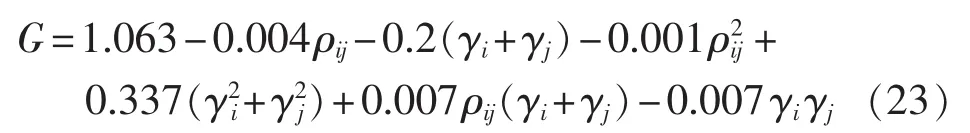
其中，γi、γj分别为变量 xi、xj的方差系数，γi=σi/μi，γj=σj/μj。

根据正交变换技术，相关的标准正态随机变量Y与不相关的标准正态随机变量的转换关系为：

其中，转换矩阵B满足BBT=CY，可通过Cholesky分解获得。

3.2 计算步骤

按照以上描述，电压稳定概率评估流程为：

a.根据风电场风速之间的相关系数矩阵CX通过式（22）获得 CY，并对 CY进行 Cholesky分解得到正交变换矩阵B；

b.利用蒙特卡罗抽样产生一个独立的标准正态分布的采样点 Zs= ［z1，s，z2，s，…，zn，s］；

c.通过式（24），经Ys=B-1Zs变换得到随机向量Y的采样点Ys；

d.根据式（21），经过边际变换技术的逆变换得到随机向量 X 的采样点

e.将采样点xi，s代入电压稳定概率评估模型式（7）—（20），采用现代内点法加以求解，获得该采样点的输出随机变量，即负荷裕度或临界功率；

f.重复步骤b—e，直至满足采样次数需求，输出负荷裕度或临界功率的概率特征参数（均值、方差等）。

4 计算结果分析

4.1 测试系统概况

在MATLAB R2014a平台编写程序实现所提出的模型与方法，所采用的计算机是IBM-PC兼容机，CPU主频为2.19 GHz×2，内存为3 GB。为清楚展示考虑网侧变换器的DFIG风电机组无功出力对电压稳定概率分析结果的影响，尽可能排除常规无功电源出力对计算结果的干扰，本文任意选择非常规无功电源节点作为风电场接入节点。表1是本文参考文献［10］和［22］得到的 4个风电场参数，分别接入IEEE 118 节点系统的节点 23、39、56、114 和 IEEE 300 节点系统的节点 21、27、37、160，表中电流与电抗均为标幺值。需要注意的是，表1中网侧变换器受不同控制方案等影响，配置容量有所不同，根据现有研究本文将之设定为风电机组容量的1/20～1/3。而风电机组最大定子电流、最大转子电流均由各自的绕组温升限制所决定，且定子和转子绕组的运行环境相同，故本文将二者标幺值设定相近。

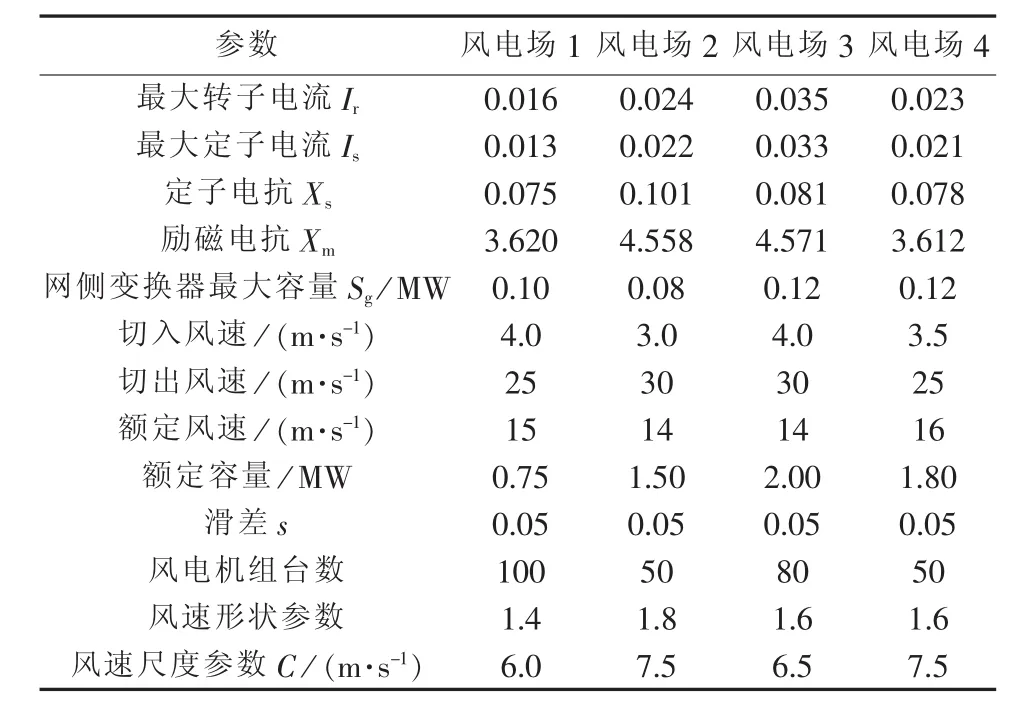
表1 各风电场参数Table 1 Parameters of wind farms

4.2 电压稳定临界功率的概率分析

风电机组的有功功率随风速波动而变化，根据DFIG风电机组的无功特性式（6），风电场1的各台机组恒电压运行时，其无功出力上、下边界随风速的变化规律如图3所示。风电机组的额定风速和切出风速主要由风电机组的机械性能所决定。当风速在额定风速和切出风速之间时，风电机组接近于其机械性能极限，但发电机组本身的最大定子电流和最大转子电流等电气性能还未达到极限。所以根据式（6），此时DFIG风电机组仍可保持较大无功调节能力，而不出现定子或转子电流越限。根据风电场风速的概率分布情况，可以确定风电场1的无功出力上、下限制的累积概率分布，如图4所示。显然考虑网侧变换器后，增强了风电场输出和吸收无功功率的能力，其无功出力上、下界均有所增大，提升了风电场的无功调压能力。

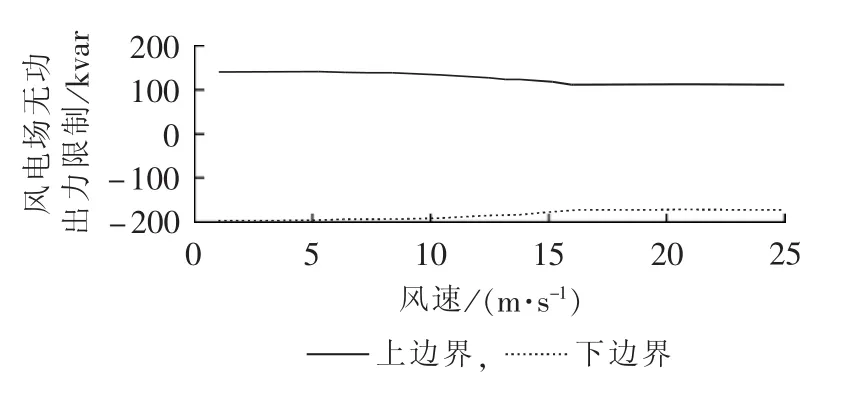
图3 风速对风电场无功功率的影响Fig.3 Impact of wind speed on reactive power of wind farm

图4 风电场无功功率限制的累积概率分布Fig.4 Cumulative probability distribution of reactive power limit of wind farm

所提模型DFIG风电机组恒电压运行，作为对比的传统模型是风电机组恒功率因数方式运行。本文模型将风电场作为PV节点，而传统模型将风电场简化处理为PQ节点，忽视了风电机组输出无功对系统电压稳定的贡献。

图5是IEEE 118节点系统静态电压稳定临界功率的概率密度分布，图6是IEEE 300节点系统临界功率的累积概率分布。表2中是IEEE 118和300节点系统传统模型和所提模型获得的临界功率均值和标准差。显然本文模型得到的临界功率均值较传统模型更大，这是因为DFIG风电机组恒电压运行输出的可调无功功率，有利于提升系统的电压稳定性。若忽略DFIG风电机组的无功功率注入，对系统电压稳定性的分析存在一定程度的低估。同时，DFIG风电机组恒电压运行时的有功出力和无功调压能力均受风速随机性影响，使得本文电压稳定概率分析结果对风速随机波动更为敏感，所得到的临界功率标准差更大，分布范围也更大。

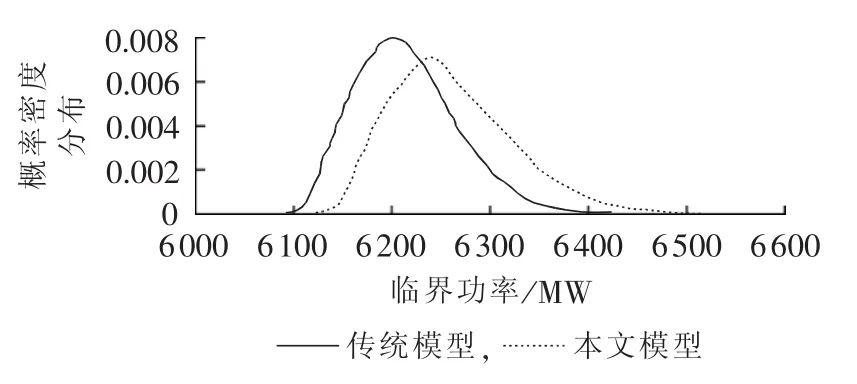
图5 IEEE 118节点系统临界功率的概率密度分布Fig.5 Probability density distribution of critical power of IEEE 118-bus system

图6 IEEE 300节点系统临界功率的累积分布Fig.6 Cumulative distribution of critical power of IEEE 300-bus system

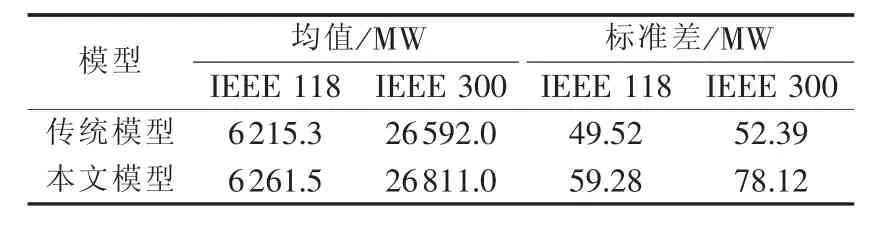
表2 各系统临界功率的均值和标准差Table 2 Mean and standard deviation of critical power for two systems

4.3 风速相关性对临界功率的影响

风电场常集中建设在风能资源比较密集的地区，处于同一风带，导致风电场随机波动的风速具有一定的相关性。表3中是不同风速相关系数时，采用传统模型和本文模型得到的电压稳定临界功率的均值和标准差。图7和8表达了临界功率均值和标准差的变化趋势。随着相关系数的增大，临界功率的均值变化不大，而其标准差明显增大。说明风速相关性对系统的电压稳定性增强或减弱没有影响，但是其增大了风速随机性对电压稳定性的影响。为避免对电力系统电压稳定性估计不足的问题，风速的相关性是不可忽略的。由于DFIG风电机组恒电压运行时，风电场的有功出力和无功调压能力均受风速相关性影响，从而本文模型结果与传统模型相比，受风速相关性的影响更大。

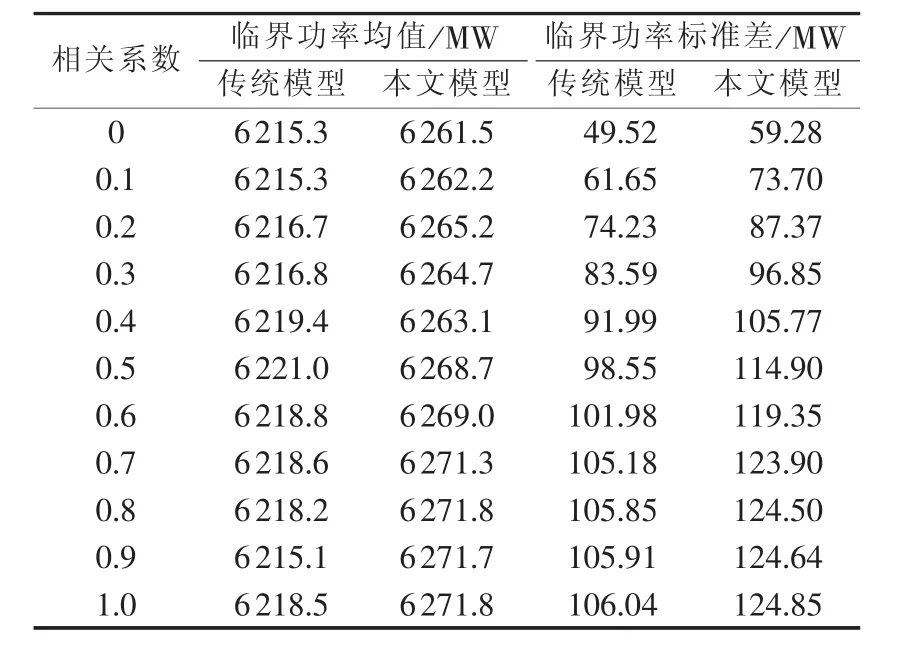
表3 风速相关性对临界功率的影响Table 3 Impact of wind speed correlation on critical power

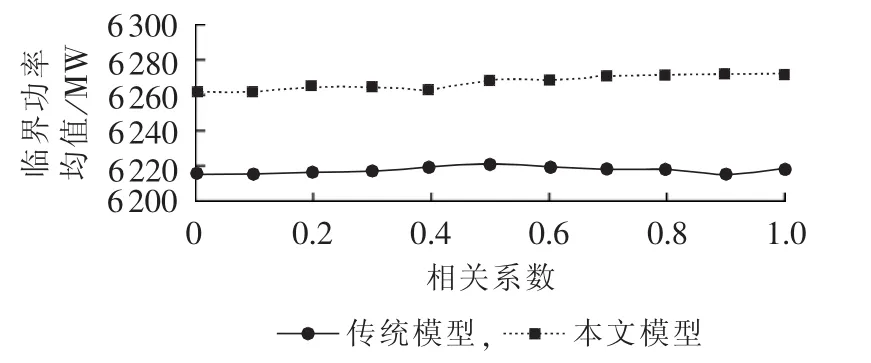
图7 风速相关性对临界功率均值的影响Fig.7 Impact of wind speed correlation on mean of critical power

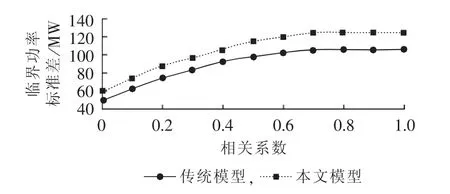
图8 风速相关性对临界功率标准差的影响Fig.8 Impact of wind speed correlation on standard deviation of critical power

5 结论

本文研究了含DFIG风电机组的电压稳定概率分析问题，推演了DFIG风电机组和网侧变换器的注入无功功率，构建出考虑DFIG风电机组无功极限的电压稳定概率分析模型，并采用蒙特卡罗法结合内点法加以求解，使得电压稳定概率分析结果更贴近实际情况。

通过IEEE 118和300节点系统的计算结果得到如下结论。

a.将风电场作为恒电压运行的PV节点，能够发挥风机输出无功功率对系统电压稳定的贡献。与此同时，由于风电机组有功出力和无功调压能力都将受风速随机性影响，使得系统的电压稳定性对风速随机波动更敏感，所得的临界功率标准差更大。

b.风速相关性对临界功率的均值影响不大，对标准差影响较大，说明其对系统的电压稳定性增强或减弱没有影响，但是其增大了风速随机性对电压稳定性的影响。

［1］中华人民共和国国务院新闻办公室.《中国的能源政策（2012）》白皮书［EB/OL］.（2012-11-04）［2015－03－09］.http：∥www.gov.cn/jrzg/2012-10 /24 /content_2250377.htm.

［2］薛禹胜，雷兴，薛峰，等.关于风电不确定性对电力系统影响的评述［J］.中国电机工程学报，2014，34（29）：5029-5040.XUE Yusheng，LEI Xing，XUE Feng，et al.A review on impacts of wind power uncertainties on power systems［J］.Proceedings of the CSEE，2014，34（29）：5029-5040.

［3］张红光，张粒子，陈树勇，等.大容量风电场接入电网的暂态稳定特性和调度对策研究［J］.中国电机工程学报，2007，27（31）：45-51.ZHANG Hongguang，ZHANG Lizi，CHEN Shuyong，et al.Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms［J］.Proceedings of the CSEE，2007，27（31）：45-51.

［4］于汀，蒲天骄，刘广一，等.含大规模风电的电网AVC研究与应用［J］.电力自动化设备，2015，35（10）：81-86.YU Ting，PU Tianjiao，LIU Guangyi，et al.AVC research and application for grid with large-scale wind power［J］.Electric Power Automation Equipment，2015，35（10）：81-86.

［5］周明，元博，张小平，等.基于SDE的含风电电力系统随机小干扰稳定分析［J］.中国电机工程学报，2014，34（10）：1575-1582.ZHOU Ming，YUAN Bo，ZHANG Xiaoping，et al.Stochastic small signal stability analysis of wind power integrated power systems based on stochastic differential equations［J］.Proceedings of the CSEE，2014，34（10）：1575-1582.

［6］郭小江，赵丽莉，汤奕，等.风火打捆交直流外送系统功角暂态稳定研究［J］.中国电机工程学报，2013，33（22）：19-25.GUO Xiaojiang，ZHAO Lili，TANG Yi，etal.Studyon angle transient stability for wind-thermal-bundled power transmitted by AC/DC system［J］.Proceeding of the CSEE，2013，33（22）：19-25.

［7］HOSSAIN M J，POTA H R，MAHMUD M A，et al.Investigation of the impacts of large-scale wind power penetration on the angle and voltage stability of power systems［J］.IEEE System Journal，2012，6（1）：76-84.

［8］许晓菲，牟涛，贾琳，等.大规模风电汇集系统静态电压稳定实用判据与控制［J］.电力系统自动化，2014，38（9）：15-19.XU Xiaofei，MU Tao，JIA Lin，et al.Practical criteria of static voltage stability in power systems with high wind penetration［J］.Automation of Electric Power Systems，2014，38（9）：15-19.

［9］HA T L，SANTOSO S，THANG Q N.Augmenting wind power penetration and grid voltage stability limits using ESS：application design，sizing，and a case study［J］.IEEE Transactions on Power Systems，2012，27（1）：161-171.

［10］张瑞明，张新燕.基于普通异步发电机和双馈风力发电机静态数学模型的系统静态电压稳定性研究［J］.电网技术，2011，35（1）：175-179.ZHANG Ruiming，ZHANG Xinyan.Sutdy on static voltage stability of power system based on static models of common and double-fed asynchronous generators［J］.Power System Technology，2011，35（1）：175-179.

［11］王敏，丁明.考虑分布式电源的静态电压稳定概率评估［J］.中国电机工程学报，2010，30（25）：17-22.WANG Min，DING Ming.Probabilistic evaluation of static voltage stability taking account of distribute generation［J］.Proceedings of the CSEE，2010，30（25）：17-22.

［12］鲍海波，韦化.考虑风电的电压稳定概率评估的随机响应面法［J］.中国电机工程学报，2012，32（13）：77-85.BAO Haibo，WEI Hua.Stochastic response surface method for probabilistic evaluation ofvoltage stabilityconsidering wind power［J］.Proceedings of the CSEE，2012，32（13）：77-85.

［13］谢应昭，卢继平.基于多项式正态变换和最大熵估计的含风电系统电压稳定概率分析［J］.电力自动化设备，2015，35（10）：66-73.XIE Yingzhao，LU Jiping.Probabilistic voltage stability analysis based on polynomial normal transformation and maximum entropy estimation for power system containing wind power［J］.Electric Power Automation Equipment，2015，35（10）：66-73.

［14］石立宝，赵阳，倪以信，等.计及风电间歇性的电力系统电压稳定评估（英文）［J］.电力系统自动化，2013，37（7）：18-24.SHI Libao，ZHAO Yang，NI Yixin，et al.Voltage stability evaluation incorporating wind power intermittency［J］.Automation of Electric Power Systems，2013，37（7）：18-24.

［15］杨悦，李国庆，王振浩.基于可信性理论的含风电电力系统电压稳定概率评估［J］.电力自动化设备，2014，34（12）：6-12.YANG Yue，LI Guoqing，WANG Zhenhao.Probabilistic voltage stability assessment based on credibility theory for power sys-tem with wind farm［J］.Electric Power Automation Equipment，2014，34（12）：6-12.

［16］VITTAL E，O’MALLEY M，KEANE A.A steady-state voltage stability analysis of power systems with high penetrations of wind［J］.IEEE Transactions on Power Systems，2010，25（1）：433-442.

［17］阮佳阳，鲁宗相，乔颖，等.并网型双馈异步发电机奇异诱导分岔型电压崩溃机理［J］.中国电机工程学报，2014，34（31）：5467-5476.RUAN Jiayang，LU Zongxiang，QIAO Ying，et al.Study on voltage collapse caused by singularity-induced bifurcation of gridconnected doubly-fed induction generator［J］.Proceedings of the CSEE，2014，34（31）：5467-5476.

［18］丁明，李宾宾，韩平平.双馈风电机组运行方式对系统电压稳定性的影响［J］.电网技术，2010，34（10）：26-31.DING Ming，LI Binbin，HAN Pingping.Impacts of operation modes of doubly-fed wind turbine generator on system voltage stability［J］.Power System Technology，2010，34（10）：26-31.

［19］LONDERO R R，AFFONSO C M，VIEIRA J P A.Long-term voltage stability analysis of variable speed wind generators［J］.IEEE Transactions on Power Systems，2015，30（1）：439-447.

［20］LASANTHA M，TIM L，SARATH P.Capability curve based enhanced reactive power control strategy for stability enhancement and network voltage management［J］.International Journal of Electrical Power&Energy Systems，2013，52：96-106.

［21］KAYIKCI M，MILANOVIC J V.Reactive power control strategies for DFIG-based plants［J］.IEEE Transactions on Energy Conversion，2007，22（2）：389-396.

［22］严干贵，王茂春，穆钢，等.双馈异步风力发电机组联网运行建模及其无功静态调节能力研究［J］.电工技术学报，2008，23（7）：98-104.YAN Gangui，WANG Maochun，MU Gang，et al.Modeling of grid-connected doubly-fed induction generator for reactive power static regulation capacity study［J］.Transactions of China Electrotechnical Society，2008，23（7）：98-104.

［23］鲍海波，韦化.考虑发电机运行极限的电压稳定临界点互补模型与算法［J］.电力系统自动化，2012，36（22）：12-18.BAO Haibo，WEI Hua.A complementary model and algorithm for critical points of static voltage stability considering generator capability limits［J］.Automation of Electric Power Systems，2012，36（22）：12-18.

［24］BILLINTON R，LI W Y.Hybrid approach for reliability evaluation of composite generation and transmission systems using Monte-Carlo simulation and enumeration technique［J］.IEE Proceedings on Generation，Transmission and Distribution，1991，138（3）：233-241.

［25］WEI H，SASAKI H，YOKOYAMA R，et al.An interior point nonlinear programming for optimal power flow problems with a novel data structure［J］.IEEE Transactions on Power Systems，1998，13（3）：870-877.

［26］CAPITANESCU F，GLAVIC M，ERNST D，et al.Interior-point based algorithms for the solution of optimal power flow problems［J］.Electric Power Systems Research，2007，77：508-517.

［27］MORALES J M，BARINGO L，CONEJO A J，et al.Probabilistic power flow with correlated wind sources［J］.IET Generation，Transmission&Distribution，2010，4（5）：641-651.