水电系统中长期发电调度多核并行逐步优化方法

冯仲恺 ，牛文静 ，廖胜利 ，程春田 ，苏华英 ，汪明清 ，唐建兴

（1.大连理工大学 水电与水信息研究所，辽宁 大连 116024；2.贵州电网公司电力调度控制中心，贵州 贵阳 550000）

0 引言

智能电网大力构建环境下的大水电系统水力、电力联系日趋复杂，其运行与管理的互动性和时效性要求不断提升［1-3］。线性规划、动态规划等传统优化方法采用串行计算编程模式，未能充分利用已有多核并行计算资源，造成资源闲置浪费［4-6］；同时在求解大规模水电优化调度问题时难以在合理时间内获取满意计算结果［7-8］，亟需新型有效的方法与途径保证水电优化调度的计算效率与求解质量［9-11］。伴随近年来计算机技术的迅猛发展，多核处理器已成为计算机硬件的标准配置，无论个人电脑还是工作站抑或服务器。传统的串行编程正逐步向并行、分布式编程转变，充分利用多核环境实现并行计算加速成为提高实际工程问题计算效率的重要途径与发展趋势［12-14］。

现有的非线性规划、混合整数规划等规划类模型及相应求解算法确实是相当高效且成熟的，但水电系统发电调度是一个复杂高维非线性约束优化问题，目前国内外能够应用于水电调度工程实际的规划类方法仍较少［6，10-11］，主要原因如下：（1）此类方法通常依赖于 CPLEX、MATLAB、LINGO等商业数学软件，需要对水库特性曲线做分段线性或近似多项式等特殊处理［4-5］以满足标准形式，在一定程度上降低了求解精度，而且标准方法的计算过程对系统用户不透明，还需要编制特定格式的文件实现调用，使得在实用化系统中的调试相对繁杂，限制了其生产应用；（2）现阶段流域梯级滚动开发的现状客观存在［10，15］，电站与机组动态投产问题突出，以贵州电网为例，在2003年引子渡电站投产后，东风电站的直接上游电站由洪家渡、普定转变为现在的洪家渡、引子渡，电站间的水力、电力等联系随之改变，需要做大量的模型更新工作，使得规划类方法在应对水电系统的可扩展性需求时面临困难；（3）规划类方法难以跟踪电网和流域日常运行中的动态变化条件［12-13，15］，例如，某年乌江渡电站1号机组检修工作提前4 d完成，使得该电站原定的最大发电流量、检修容量、发电能力等多个方面发生变化，进而引发相应约束条件发生变动，需要多次调整和构建指定格式的相关数据，增大了实践难度。因此，笔者暂时未将研究重点放在规划类方法上，而是对现有的工程实用化方法开展并行改进，以保证快速获取合理调度结果。

逐步优化算法POA（Progressive Optimality Algorithm）作为动态规划的经典改进算法，将多阶段决策问题分解为若干两阶段子问题进行计算，在提高效率的同时能保证收敛至总体最优解［16-17］，因而在水电调度、水火协调、防洪调度、火电开机等多个领域得到广泛应用［18-21］，其实用性与易用性也通过了诸多实际工程的检验。然而，在应用中发现：随着系统规模增大，POA仍存在计算耗时过长等问题，难以满足水电计划编制的时效性要求［17，19］。 为此，本文在 POA 并行性分析基础上提出多核并行逐步优化算法MPPOA（Multi-core Parallel Progressive Optimality Algorithm），并利用Fork/Join并行框架［12-13］在多核环境下开展仿真调度，结果表明本文方法结合并行计算与POA优点，可有效均衡计算精度与运算效率。

1 水电系统发电调度模型

1.1 目标函数

通常水电系统根据各水电站水库的调蓄能力、调度期始末水位及区间径流过程等条件，综合考虑水位限制、出力限制等多种复杂约束，合理控制各水库在不同时期的水位升降过程，使得调度期内系统总体效益达到最优，目标函数可用下式表示：

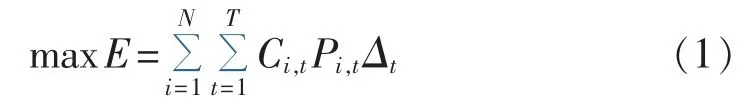
其中，Ci，t为水电站 i在时段 t效益系数，若∀i，t，Ci，t=1，则式（1）为发电量最大模型，若 Ci，t为水电站 i在时段t的电价系数，则式（1）转化为发电效益最大模型；E为调度期内总效益；N为电站数目；T为调度周期；Pi，t为水电站 i在时段 t的出力（kW），Pi，t=AiQi，tHi，t，Ai为水电站i出力系数，Qi，t为水电站i在时段t的发电流量（m3/s），Hi，t为水电站 i在时段 t的水头（m）；Δt为时段t的小时数（h）。

1.2 约束条件

（1）始末水位约束：

其中为水电站i的初始水位（m）为水电站i的末水位（m）。

（2）水量平衡方程：

其中，Vi，t为水电站 i在时段 t的库容（m3）；Si为水电站i的上游水库集合，对龙头水库有分别为水电站i在时段t的区间流量、出库流量和弃水流量（m3/s）。

（3）水位约束：

其中，Zi，t为水电站 i在时段 t的水位（m）分别为水电站i在时段t的水位上、下限。通常情况下取为水电站的死水位在汛期和非汛期分别为水电站的汛限水位、正常高水位。

（4）发电流量约束：

其中分别为水电站 i在时段 t发电流量上、下限，取决于机组的过流能力、检修计划等。

（5）出库流量约束：

（6）电站出力约束：

其中分别为水电站 i在时段 t出力上、下限，取决于电站技术出力要求、检修容量、装机容量等。

（7）系统总出力限制：

其中分别为时段 t水电系统带宽上、下限（kW）。

（8）其他约束：根据具体问题所需考虑的相关约束。

2 POA

2.1 POA原理

POA 是由 H.R.Howson［16］等人于 1975 年提出用于求解多阶段多状态优化问题的动态规划改进算法。依据逐次最优化原理，即“最优路线具有这样的性质，每对决策集合相对于它的初始值和终止值而言是最优的”，POA将多阶段问题分解为若干两阶段子问题，每次计算均固定其他阶段变量，只优化调整当前所选两阶段变量，并将本次优化结果作为下次优化计算的初始条件，如此逐时段进行，反复循环直至收敛。

在应用POA求解水电优化调度过程中，状态变量取为各水电站不同时段水位，决策变量取为相应出库流量，步骤如下。

（1）由人工经验或常规调度等确定各水电站在不同时刻的初始轨迹。

（2）设t=T－1，固定其余阶段各水电站状态，离散时段t各水电站水位并构造相应状态组合，从中优选最优状态组合，使时段t-1和t+1内的系统总效益之和达到最优。同理对下一阶段进行寻优，直至获得当前轮次各计算时段所有电站最优状态组合。

（3）将本次迭代求得的最优轨迹作为下次迭代的初始轨迹，重复步骤（2）直至相邻2次迭代的最优轨迹完全相同，此时停止计算并输出最优轨迹。

2.2 POA并行性分析

从2.1节可知，POA子问题计算量最大部分在于对所求时段各水电站状态进行离散并加以组合，从中获取最优状态组合。假设系统共有N座电站，各电站状态均取k份离散状态，由排列组合原理可知，所求时段t状态组合数目at为：

定义系统任意两相邻时段状态组合需要单次调节计算。此时，时段t-1和t+1均有1个状态组合，两相邻时段（t-1和t、t和t+1）均需进行at次状态组合的调节计算，单个子问题计算量为：

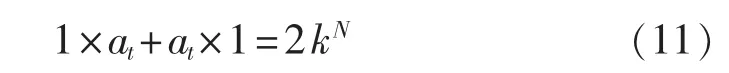
显然，POA时间复杂度为O（kN），其运算耗时将随电站与状态离散数目增多呈指数增长。然而，常规POA采用传统串行计算模式，依次对状态组合进行调节计算，如图1所示，此时庞大的运算量积压于单个处理器，将造成其他处理器计算资源的浪费和求解效率的大幅降低，难以满足大规模水电系统发电调度计划编制的时效性要求。与此同时，POA子问题中各状态组合分别代表一种调度决策过程，任意两状态组合之间相互独立、无直接联系，改变各状态组合的计算次序并不影响最终结果。由此可知，POA具有良好并行性，具备数据驱动并行计算模式的特点，可在状态组合级别上实现同步计算。因此，本文提出在多核环境下将POA子问题的状态组合分配至不同计算单元实现并行求解，以充分利用已有计算资源，减少运算耗时，提高水电调度计划编制效率。

图1 POA串行计算示意Fig.1 Schematic diagram of serial computation of POA

3 MPPOA

3.1 Fork/Join框架

Fork/Join框架是一种基于分治策略处理海量数据计算、充分利用多核CPU计算能力的并行计算框架，通过问题分解、并行计算、结果合并3个主要步骤实现并行求解。其基本思想是：首先采用“分治法”将难以直接求解的大规模复杂问题分解为数个规模较小、相互独立且可直接求解的子问题，然后递归求解获取各子问题最优解，最后合并各子问题的解得到原问题的解。

Fork/Join框架在任务分解过程中定义阈值用以控制子问题规模，其并行执行过程如图2所示。原问题为难以直接进行求解的大规模复杂问题，采用分治思想将其划分为多个子问题，若子问题规模大于阈值则持续划分为更小规模子问题，否则提交给内核线程池执行；上级任务依赖于其所划分的子任务，只有将所有子任务的计算结果合并后方能获得相应结果。其中阈值的大小对并行效率影响较大：若阈值过大，则子任务数目较少、无法充分利用多核资源；若阈值偏小，则子任务数目较多、任务管理开销加大。因此，为充分利用资源、提高计算效率，按下式确定阈值w：

其中表示不小于x的最小整数；a为任务计算规模；P为CPU核数。

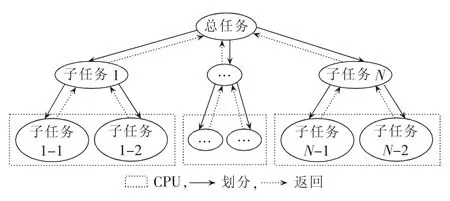
图2 Fork/Join框架示意Fig.2 Schematic diagram of Fork/Join framework

3.2 基于Fork/Join框架的MPPOA实现

MPPOA以POA为基础执行框架，首先将多阶段子问题分解为若干两阶段子问题，然后利用Fork/Join框架将所有状态组合的调节计算分解为若干子任务，分别交由多个CPU实现并行计算，如图3所示，步骤如下。

（1）由主线程计算优化阶段状态组合总数目，并生成设定数量的线程池。

（2）由式（12）计算阈值并确定子任务数目，将主线程中状态组合分解至各线程池，直至各子任务规模不大于设定阈值。

图3 MPPOA并行计算示意Fig.3 Schematic diagram of multi-core parallel computation of POA

（3）各子线程根据得到状态组合及各电站基础特性数据，对当前任务集合中各状态组合进行目标函数及相应惩罚项的计算，而后将最优结果返回并存入主线程。

（4）主线程合并各子线程计算结果，获取当前最优状态组合及相应计算结果。

3.3 MPPOA性能分析

（1）从计算模式上看，POA仅能利用单个CPU进行串行计算，造成其他CPU资源闲置，而MPPOA将大规模复杂问题分解至多个CPU开展并行计算，同时Fork/Join框架的“工作窃取”机制可有效提升工作线程利用率，实现负载均衡；

（2）从复杂度上看，MPPOA在多核环境下利用Fork/Join框架实现并行计算，假设分配至P个CPU，则时间复杂度由 POA 的 O（kN）降至 O（kN/P）；

（3）从求解效率上看，MPPOA将任务分配至多个计算单元开展并行计算，显然可以充分利用已有资源，大幅缩短运算时间，有效提升计算效率；

（4）从计算规模上看，MPPOA计算规模将随CPU内核数目的增多而提升，且在相同时间内能够完成的工作量更多；

（5）从计算结果上看，MPPOA充分结合POA良好搜索性能和并行技术的计算加速等优点，有效保证水电系统优化调度计算的科学性和时效性。

3.4 MPPOA求解水电发电调度问题

利用MPPOA求解水电优化调度步骤如下。

（1）设置终止精度ε、状态离散数目k等参数。

（2）由常规调度方法确定水位变化序列Z0。

（3）令 t=T-1。

（4）由时段 t各电站初始状态 Zi，t及相应搜索步长 hi，t构造状态组合。

（5）利用3.2节方法开展并行计算，获取最优状态组合及相应结果。

（6）判定是否满足式（13），若满足则转至步骤（7）；否则令转至步骤（4）。

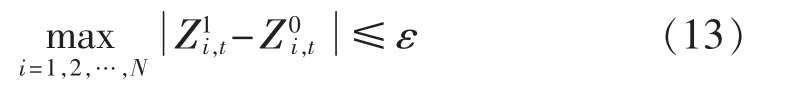
（7）令 t=t-1，若 t＞0，则转至步骤（4）；否则转至步骤（8）。

（8）此时各水电站水位序列为Z1，判定是否满足式（14），若满足转至步骤（9）；否则，将搜索步长缩减一半，然后转至步骤（3）。

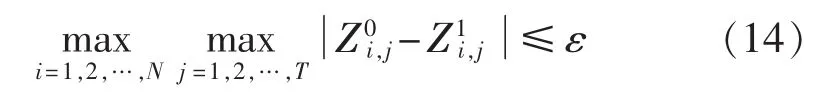
（9）停止计算，输出各水电站最优水位序列。

4 工程应用

4.1 应用背景

下面以乌江流域长期优化调度作为研究对象对MPPOA进行验证。乌江流域是我国十三大水电基地之一，各水电站的建设任务均以发电为主，肩负着我国“西电东送”战略任务的历史使命；同时作为贵州省最重要的水电基地，承担贵州电网的发电、调峰、调频等任务。乌江流域拓扑结构见图4，电站调节性能多样，涵盖多年、不完全年及日调节等多种调节性能。本文以年度计划编制为例开展研究，目标函数采用发电量最大模型，调度周期为1 a，调度时段为1个月，总时段数为12。采用JAVA语言编制相应算法程序，在DELL 6850服务器上通过设置运行核数实现2核、4核、8核并行计算。

图4 梯级水库拓扑结构图Fig.4 Topology of cascaded reservoirs

4.2 不同来水情境下多种方法比较

选取丰、平、枯3种不同频率来水开展性能测试，分别采用本文方法与动态规划逐次逼近法（DPSA）进行求解，其中MPPOA采用8核并行，计算结果如表1所示。从耗时上看，3种典型年来水条件下，MPPOA约需POA耗时的15%即可收敛，求解时间明显缩短，计算效率显著提升；与DPSA相当，总时间仍不足8 s，这在水电系统长期优化调度中是可以接受的。从发电量上看，相比于DPSA，不同情境下的MPPOA与POA优化结果均有较大幅度提升，例如丰水年条件下约增发5×105MW·h电量，这是由于DPSA依次对各电站进行求解，未能有效考虑梯级水电站间的协调效应，使其搜索性能在一定程度上受到限制；POA可保证收敛至总体最优解，搜索性能良好；MPPOA未改变方法的寻优机制，优化结果与POA完全一致。综上，DPSA以牺牲优化结果换取计算效率的提升，而MPPOA结合了并行计算与POA的优点，有效保证求解精度与运算效率。

4.3 不同系统出力限制下MPPOA有效性检验

为检验本文方法在不同系统约束下的性能表现，选用某年实测来水作为输入径流，并采取多种水电出力限制约束加以验证。表2列出了MPPOA详细计算结果，可以看出，通过引入水电系统总出力约束，能有效实现水能资源的均衡分布。系统出力限制的增加虽然在一定程度上降低了发电量，但是在枯水期的总出力得到提升，如方案5的总电量较方案1降低了1.3%，但相应系统最小出力增加了3倍，实现了水能资源的合理蓄放，有利于水能与风能、光伏能等间歇性能源的互补联合调度。

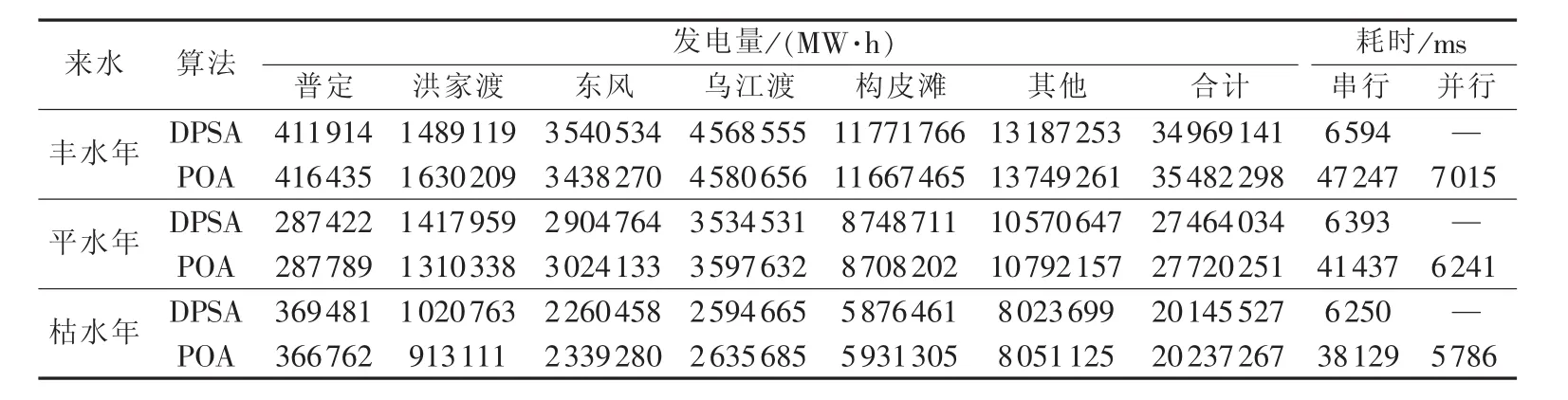
表1 不同方法计算结果Table 1 Calculative results of different methods

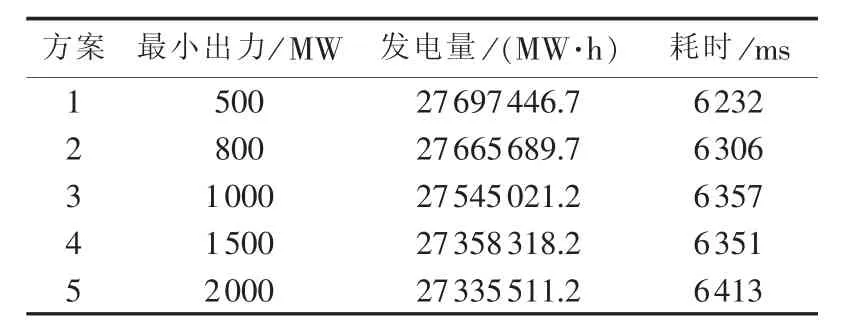
表2 不同系统约束下MPPOA计算结果Table 2 Calculative results of MPPOA for different system constraints

4.4 不同计算核数比较

进一步开展POA与MPPOA在不同内核下性能对比，下面引入2个常用于评价并行系统或程序并行化后的性能和效果指标：加速比SP和效率EP。指标计算公式如下：

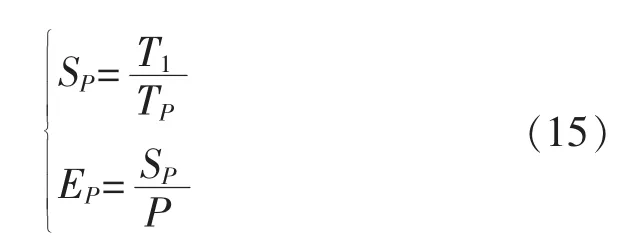
其中，T1为串行计算耗时；TP为并行方法在P个处理器上的时间。

表3列出在平水年来水条件下，POA与MPPOA不同状态离散数目的计算结果对比。

（1）从耗时和发电量上看，随着状态离散数目增加，两方法搜索能力得到增强，发电量均逐渐增大，但增幅并不明显，而计算规模呈指数增长，POA耗时显著延长：k由3增加至5时，发电量仅增加4.6×104MW·h，但POA耗时增至约2.4倍；k由7增加至9，发电量不再增加，而POA耗时增幅高达2060 s，显然已无法满足实际工程的时效性需求。MPPOA与串行方法相比，大幅缩减计算耗时，且随着CPU核数的增加，性能优势更加显著：在k=3时，串行耗时分别为2核、4核和8核环境下并行计算的1.83倍、3.41倍和6.64倍；在k=9时，2核、4核和8核环境下并行计算耗时分别减少1223 s、1833 s和2176 s。

（2）从加速比上看，MPPOA在不同内核环境下均获得良好加速比，且加速比与内核呈正相关关系；在相同内核环境下，计算任务越大，加速比越大，且越接近于理想加速比：在k=5时，2核、4核和8核环境下的加速比分别为1.89、3.53和6.80；在2核环境下，k 取 3、5、7 时，加速比分别达到 1.83、1.89 和 1.91，与理想加速比（SP=2）差值逐渐缩小。

（3）从效率上看，在计算任务相同时，并行效率随内核增加呈下降趋势：在k=5时，2核、4核和8核环境下并行效率分别为0.94、0.88和0.85，下降趋势明显。这是由于在相同计算任务下，随着CPU数目增加，内核间通信逐渐增多，同时线程池对各子线程的调度管理消耗增加，导致计算效率降低。

综上，MPPOA结合了并行技术与POA优点，有效保证水电系统优化调度计算的时效性和结果的准确性，且计算规模越大，效率优势越突出；此外，随着计算机硬件资源的提升，MPPOA在相同时间内能够完成更多的工作量。

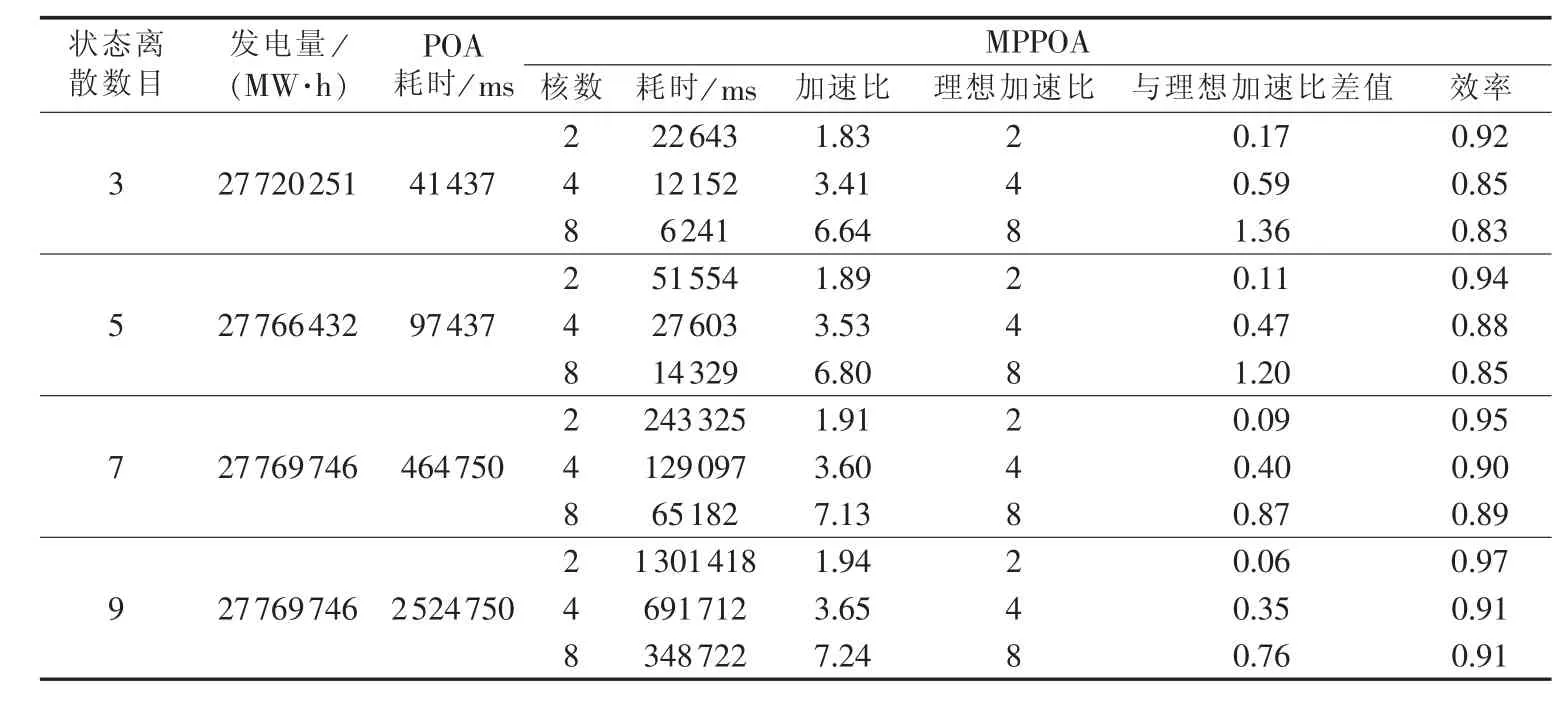
表3 不同情景下计算结果对比Table 3 Comparison of calculative results among different scenarios

5 结论

本文立足智能电网精细化调度需求与高性能计算发展趋势，探讨分析了POA的并行化原理，提出了结合并行技术和POA的MPPOA。该方法原理清晰、可操作性强，在保证计算精度的同时，充分利用现有多核资源提升求解效率，无需追加额外硬件，其高效性与实用性经受了贵州电网工程实践的有效检验，为水电发电调度计划的高效科学编制提供了一种可选方法。由于POA应用的广泛性，本文所提方法可推广至短期水电调度、水火协调、防洪调度等多个领域；同时，本文仅结合Fork/Join框架在多核环境下实现计算加速，在未来研究中可结合GPU并行计算及分布式计算等高性能计算技术进一步提升方法的计算效率。

［1］纪昌明，周婷，王丽萍，等.水库水电站中长期隐随机优化调度综述［J］.电力系统自动化，2013，37（16）：129-135.JI Changming，ZHOU Ting，WANG Liping，et al.A review on implicit stochastic optimization for medium-long term operation of reservoirs and hydropower stations［J］.Automation of Electric Power Systems，2013，37（16）：129-135.

［2］张伯明，孙宏斌，吴文传，等.智能电网控制中心技术的未来发展［J］.电力系统自动化，2009，33（17）：21-28.ZHANG Boming，SUN Hongbin，WU Wenchuan，etal.Future development of control center technologies for smart grid ［J］.Automation of Electric Power Systems，2009，33（17）：21-28.

［3］翁毅选，邓长虹，黄文涛，等.基于最优动态闭环控制的水火电互联大电网自动发电控制策略［J］.电力自动化设备，2013，33（3）：66-71.WENG Yixuan，DENG Changhong，HUANG Wentao，et al.AGC based on optimal dynamic closed-loop control for interconnected power grid of hydro and thermal power plants［J］.Electric Power Automation Equipment，2013，33（3）：66-71.

［4］YEH W W G.Reservoir management and operations models：a state-of-the-art review［J］.Water Resources Research，1985，21（12）：1797-1818.

［5］陈森林.水电站水库运行与调度［M］.北京：中国电力出版社，2008：152-154.

［6］LABADIE J W.Optimal operation of multireservoir systems：stateof-the-art review［J］.Journal of Water Resources Planning and Management，2004，130（2）：93-111.

［7］张智晟，樊秀娟，林涛.基于量子蚁群优化算法的梯级水电系统经济调度［J］.电力自动化设备，2010，30（10）：17-21.ZHANG Zhisheng，FAN Xiujuan，LIN Tao.Economic dispatch of cascaded hydropower system based on quantum ant colony optimization algorithm［J］.Electric Power Automation Equipment，2010，30（10）：17-21.

［8］张秀霞，王爽心，吴冠玮.基于混沌遗传和模糊决策算法的多目标负荷经济调度［J］.电力自动化设备，2009，29（1）：94-99.ZHANG Xiuxia，WANG Shuangxin，WU Guanwei.Multi-objective economic load dispatching based on chaos genetic algorithm and fuzzy decision［J］.Electric Power Automation Equipment，2009，29（1）：94-99.

［9］胡国强，贺仁睦.梯级水电站长期多目标模糊优化调度新模型［J］.电力自动化设备，2007，27（4）：23-27.HU Guoqiang，HE Renmu.Long-term multi-objective fuzzy optimization scheduling model of cascaded hydroelectric stations［J］.Electric Power Automation Equipment，2007，27（4）：23-27.

［10］CHENG Chuntian，SHEN Jianjian，WU Xinyu，et al.Operation challenges for fast-growing China’s hydropower systems and respondence to energy saving and emission reduction［J］.Renewable and Sustainable Energy Reviews，2012，16（5）：2386-2393.

［11］郭生练，陈炯宏，刘攀，等.水库群联合优化调度研究进展与展望［J］.水科学进展，2010，21（4）：496-503.GUO Shenglian，CHEN Jionghong，LIU Pan，et al.State-of-theart review of joint operation for multi-reservoir systems ［J］.Advances in Water Science，2010，21（4）：496-503.

［12］张东晓，王静，范炜，等.基于并行遗传算法的水电站群中期优化调度［J］.电力自动化设备，2012，32（12）：87-91.ZHANG Dongxiao，WANG Jing，FAN Wei，et al.Midterm optimal operation based on parallel genetic algorithm for hydropower stations［J］.Electric Power Automation Equipment，2012，32（12）：87-91.

［13］申俊华，廖胜利，程春田，等.基于多核并行的中期火电开机优化算法［J］.电力自动化设备，2011，31（6）：28-33.SHEN Junhua，LIAO Shengli，CHENG Chuntian，et al.Optimization of medium-term thermal power boot based on multi-core parallel algorithm［J］.Electric Power Automation Equipment，2011，31（6）：28-33.

［14］陈立华，梅亚东，麻荣永.并行遗传算法在雅砻江梯级水库群优化调度中的应用［J］.水力发电学报，2010，29（6）：66-70.CHEN Lihua，MEI Yadong，MA Rongyong.Parallel genetic algorithm and its application to optimal operation of the Yalong river cascade reservoirs［J］.Journal of Hydroelectric Engineering，2010，29（6）：66-70.

［15］ZHOU J，ZHANG Y，ZHANG R，et al.Integrated optimization of hydroelectric energy in the upper and middle Yangtze River［J］.Renewable and Sustainable Energy Reviews，2015，45：481-512.

［16］HOWSON H R，SANCHO N G F.A new algorithm for the solution of multi-state dynamic programming problems［J］.Mathematical Programming，1975，8（1）：104-116.

［17］冯仲恺，廖胜利，程春田，等.库群长期优化调度的正交逐步优化算法［J］.水利学报，2014，45（8）：903-911.FENG Zhongkai，LIAO Shengli，CHENG Chuntian，et al.Orthogonal progressive optimality algorithm for long-term optimal operation of multi-reservoir system［J］.Journal of Hydraulic Engineering，2014，45（8）：903-911.

［18］NANDA J，BIJWE P R.Optimal hydrothermal scheduling with cascaded plants using progressive optimality algorithm［J］.IEEE Transactions on Power Apparatus&Systems，1981，pas-100（4）：2093-2099.

［19］CHENG Chuntian，SHEN Jianjian，WU Xinyu，et al.Short-term hydroscheduling with discrepant objectives using multi-step progressive optimality algrithm［J］.Journal of the American Water Resources Association，2012，48（3）：464-479.

［20］BAITao，CHANG Jianxia，CHANG Fijohn，etal.Synergistic gains from the multi-objective optimal operation ofcascade reser-voirs in the upper Yellow River basin［J］.Journal of Hydrology，2015，523：758-767.

［21］JI C，JIANG Z，SUN P，et al.Research and application of multidimensional dynamic programming in cascade reservoirs based on multilayer nested structure［J］.Journal of Water Resources Planning and Management，2015，141（7）：401-409.