基于边际成本下垂控制的自治微电网分布式经济运行控制

苏 晨，吴在军，吕振宇，窦晓波，胡敏强

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

微电网是可自治运行的小型发配电系统，往往集成多种类型的分布式电源DG（Distributed Generator）［1-2］。 传统下垂控制按照容量比例分配功率，但是由于不同类型DG的发电成本及运行特性各异，按容量分配功率易造成系统运行成本偏高。为了降低系统运行成本，需考虑各DG的成本优化分配功率，实现微电网经济运行。

微电网的经济优化运行一般采用集中式方法，由中心控制器采集全网信息，并利用集中式优化算法（例如数学规划方法［3-4］或粒子群优化算法等启发式算法［5-6］）进行模型求解，得到优化调节指令，并下发给各本地控制器，从而实现全网经济优化。文献［3］建立多目标优化模型，通过混合整数规划进行能量优化。文献［5-6］分别运用粒子群优化算法和遗传算法解决功率经济分配问题。集中式优化方法［3-6］调节精度高，但是当网络节点较多时通信量过大，对通信线路要求较高，可扩展性差；依赖中心控制器，一旦故障将导致控制失败，可靠性差。此外，启发式算法表现不稳定，不能保证收敛到最优解，因此稳定性较差。

为了克服上述集中式方法的不足，有学者提出基于无通信的自治经济下垂控制。文献［7-9］针对发电成本不同的DG，设计基于本地信息的非线性下垂控制，使得成本高的DG少出力，成本低的DG多出力，从而降低系统运行成本，但是该方法基于DG的运行成本，而非边际成本，因此只能实现经济较优，而非最优运行。此外，由于本地信息不同，自治控制无法进行全网优化，功率分配精度低，并且缺乏电压和频率的二次调节。文献［10］针对直流微电网，提出线路阻抗补偿的方式以提高功率分配精度，但是该方法需事先得知线路阻抗的大小，因此具有局限性。文献［11］提出一种自治三级控制，可实现各DG边际成本一致，但是其采用低通滤波器降低非线性下垂控制对系统稳定性的影响，动态响应较慢。文献［12］利用一致性算法实现边际成本一致，但是需挑选主导节点控制边际成本的增减方向，削弱了系统的可靠性。

本文提出基于边际成本的改进下垂控制，以实现降低系统运行成本的目的。同时引进分布式经济运行策略，通过优化所提下垂控制的参考电压，解决其功率分配精度易受线路阻抗影响的问题，实现微电网经济运行。该分布式策略基于节点地位对等的稀疏分布式网络，无中心节点，可靠性高。仿真分析验证了所提策略的有效性与优越性。

1 基于边际成本的改进下垂控制

为降低系统运行成本，本节分析不同类型DG的运行成本，在传统下垂控制的基础上提出基于边际成本的改进下垂控制。

1.1 传统下垂控制

由于低压电网的线路阻抗主要呈现阻性［13］，因此基于P-U和Q-f特性的传统下垂控制如下：

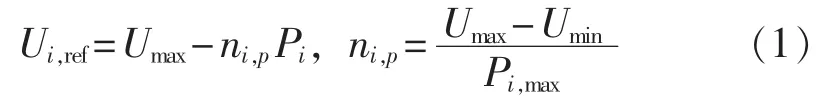
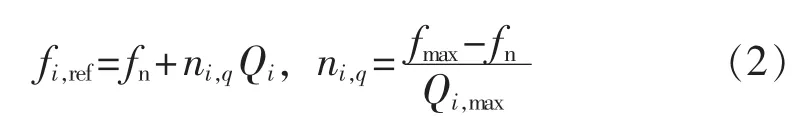
其中，Umax、Umin分别为最大和最小允许电压；fn为额定频率；fmax为最大允许频率；Pi，max、Qi，max分别为 DGi最大允许有功和无功功率。

1.2 基于边际成本的改进下垂控制

DG的运行成本主要考虑燃料费用、维护费用和逆变器的运行效率。不同类型的DG成本不同，但其成本函数可统一简化为二次函数的形式［10］：

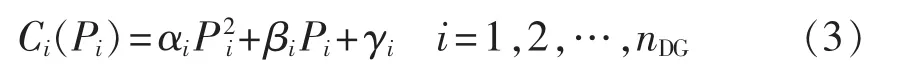
其中，αi、βi、γi为 DGi的成本系数，对于不同类型的DG如光伏电池 PV（PhotoVoltaic）、燃料电池 FC（Fuel Cell）和微型燃气轮机 MT（Micro-Turbine），系数大小及物理意义不同［10］；nDG为DG台数。

由于无功成本相比有功成本较小，因此可忽略［7］，本文主要考虑有功功率的成本，系统的总运行成本Ctotal如下：

系统稳定运行，各DG的边际成本一致时，系统的总运行成本最小［12］。

在传统P-U下垂控制的基础上，考虑各DG的边际成本，设计改进下垂控制如下：

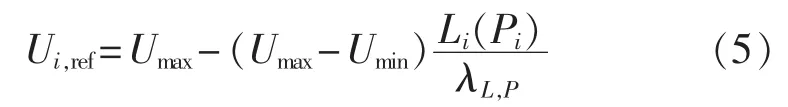
其中，Li（Pi）为 DGi的边际成本，定义为式（6）；λL，P为下垂成本系数，各DG取值相同，满足式（7）。

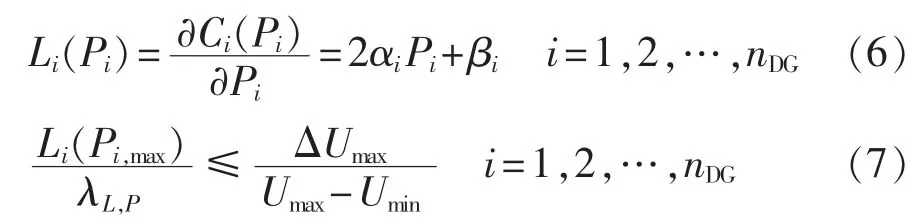
其中，ΔUmax为最大允许电压偏差量，一般为母线额定电压的5%。

1.3 与传统下垂控制的比较

传统下垂控制按照各DG容量比例分配功率，如图1（a）所示，由于未考虑DG的运行成本，若成本高的DG容量大，会导致系统运行成本偏高。所提改进下垂控制按照各DG边际成本一致分配出力，如图1（b）的U-L和L-P曲线所示，边际成本高的DG出力少，边际成本低的DG出力多，从而实现各DG边际成本相等，综合的U-P下垂曲线如图1（b）所示，因此，所提改进下垂控制可实现降低系统总运行成本的目标。

和传统下垂控制类似，基于边际成本的经济下垂控制尽管能基于本地信息自治进行功率分配，但由于线路阻抗分布不均，各DG输出电压不等，由图1（b）的U-L曲线可知，各DG的边际成本不相等，因此改进下垂控制的控制精度较低，各DG边际成本不能实现精确一致。为此，本文进一步提出基于一致性算法的分布式经济运行控制，消除线路阻抗的影响，提高控制精度。

图1 2种下垂控制Fig.1 Two kinds of droop control

2 分布式经济运行控制

2.1 分布式经济运行控制总体架构

分布式经济运行控制总体架构如图2所示。

每个DG具有一个分布式控制器 DCr（Distributed Controller），负责DG间通信和一致性计算。在分布式稀疏通信网络中，各DCr仅与相邻DCr交互信息，各DCr地位对等，不存在主导DCr，可靠性高。

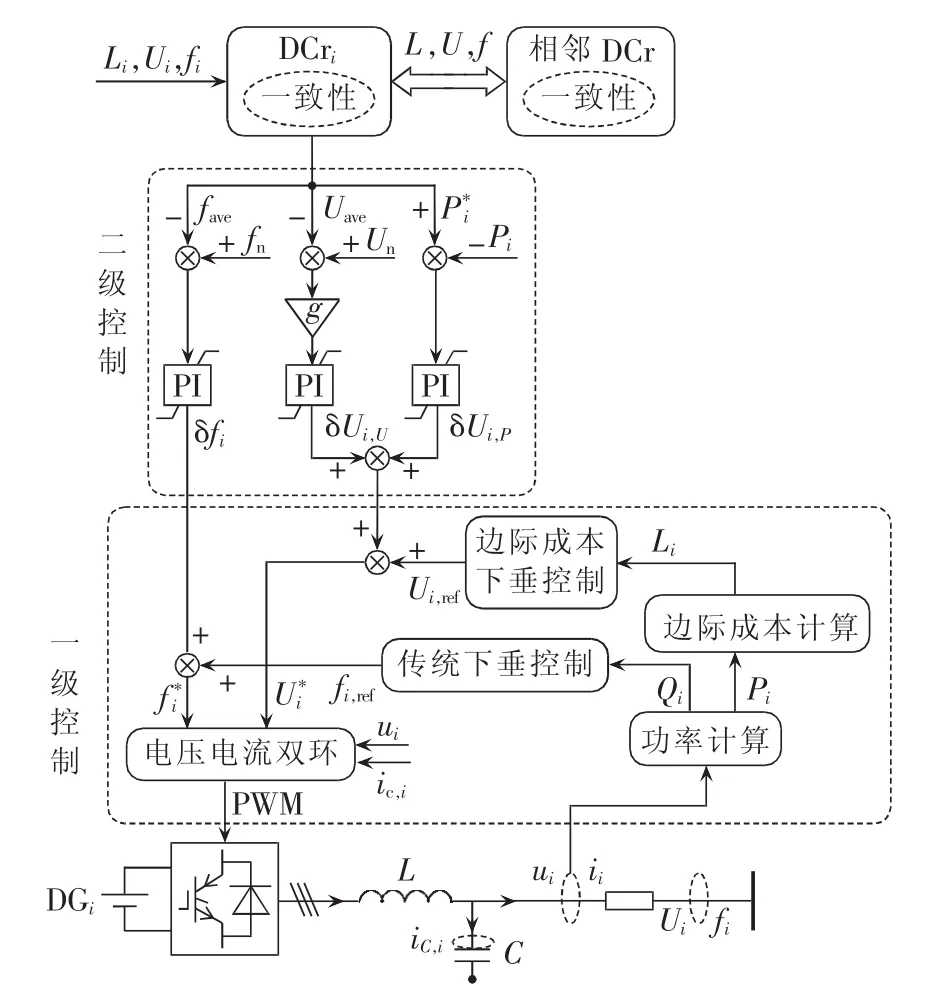
图2 所提控制策略架构Fig.2 Structure of proposed control strategy

以DGi为例，其DCri采集本地电压Ui、频率fi和边际成本Li信息，并将其发送给相邻控制器，同时接收相邻控制器的电压、频率和边际成本信息，利用一致性算法获得目标有功功率全网平均电压Uave和平均频率fave，将其输出给本地二级控制器。

二级控制基于一致性结果，通过PI控制器产生有功修正量 δUi，P和电压修正量 δUi，U修正下垂控制的参考电压，实现各DG边际成本一致，并恢复全网平均电压至额定值；频率修正量δfi修正参考频率，可恢复频率至额定值。

该策略通过对各DG输出电压和频率的调控，提高下垂控制的功率分配精度，降低系统运行成本，实现微电网经济稳定运行。

2.2 基于离散一致性的DCr

（1）离散一致性算法。

一致性算法起源于分布式计算与决策，目的是使系统中的个体状态渐近趋向于初始状态的平均值，已在随机网络、多机器人系统、集群控制等诸多领域有广泛应用。

用图G=（V，E）表示一致性问题中节点的通信网络拓扑，V=｛1，2，…，n｝表示节点的集合，E⊆V×V 表示节点的边。Ni=｛jϵV|（j，i）ϵE｝表示节点 i的邻居节点的集合。

一致性算法不需要节点和其他所有节点通信，仅需与相邻节点通信，便可使各节点共享系统的状态变量均值，通信量少且较为均衡。由于实际系统为离散控制系统，本节介绍离散一致性算法，表示为：

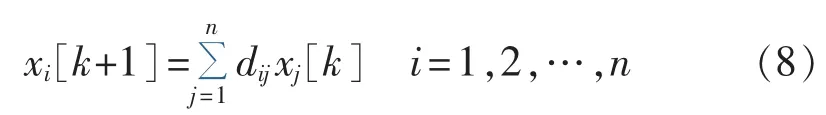
其中，xi为节点i的状态变量；k为离散时间变量；n为节点数。矩阵形式为：

其中，D为系统的状态转移矩阵，dij为其元素，若节点i与节点j之间有链路，则dij＞0，反之则为0。节点i利用自身和邻居的状态信息加权线性叠加更新xi。

若图G是强连通图并且是平衡图或D构造为双随机矩阵时，系统一致收敛于状态变量的平均值［14］，即：

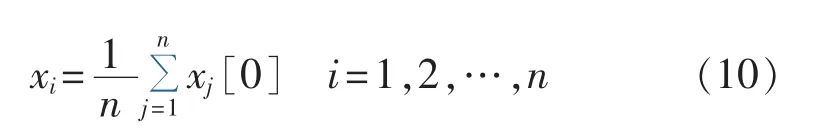
文献［14］提出一种Metropolis方法构造矩阵D为双随机矩阵，以适应网络结构的变化，保证算法具有良好的收敛性，表示为：

其中，max（ni，nj）为节点 i及其邻居节点 j所拥有的邻居数目中的最大值，ni、nj分别为节点i、j的邻居节点数；jϵNi表示节点j是节点i的邻居节点。

离散一致性算法收敛所需迭代次数K按照下式计算［14］：

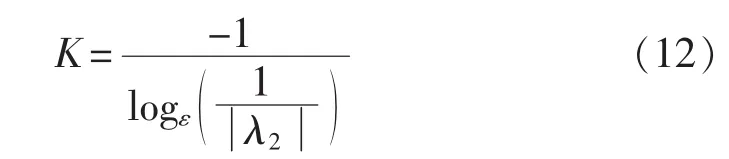
其中，ε为允许误差；λ2为矩阵D的第二大特征值，决定了一致性的收敛速度。

（2）DCr的实现。

DCr分别通过一致性算法求取平均边际成本Lave以用于二级功率优化，求取全网平均电压用于二级电压调节。此外，考虑虽然稳态时全网频率统一，但是在发生扰动的暂态过程中，各DG的频率会因变化不同步产生偏差。为了实现各DG的实时同步频率调节，通过一致性算法获取平均频率。

DCr的信息处理流程如图3所示。在DCr中设置时钟，周期设为Ts，驱动各DCr采集及交互信息，保证系统有序运行。令t=t0+kTs，简记为t=k。时钟启动，DCri采集本地边际成本 Li［0］，与邻居 DCr交互边际成本信息，检测是否收到邻居的功率饱和标识，若没有，则采用原始双随机矩阵D；若收到通知，则修改矩阵 D，再按式（13）计算 Li［k+1］。

图3 DCr信息处理流程图Fig.3 Flowchart of information processing of DCr

其中，n′为输出有功功率未饱和 DG 数目；Li［k］为DGi在第k次迭代时的边际成本。

下一时钟周期，继续交互边际成本信息和一致性迭代，如此循环直到收敛得到Lave。根据式（14）得到目标有功功率并输出给本地二级控制器进行参考电压的修正。本次迭代过程结束，重复进行下一轮迭代。

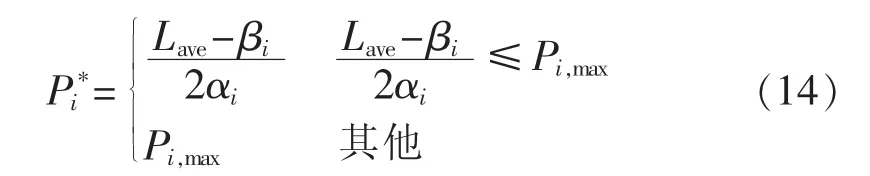
在系统重载时，由于边际成本低的DG出力大，其输出有功功率易饱和。控制时为了防止其功率越限，采取功率判断策略：由Lave得到目标有功功率，判断其是否越限，若越限，则将其限制在最大功率值，使该DG输出有功功率达到饱和状态，DCri向相邻DCr发送功率饱和标识，并且退出边际成本一致性网络，由于网络拓扑发生改变，其余DCr相应地修改边际成本一致性矩阵D，再参与平均边际成本的计算。

由于全网平均电压和频率的计算不受DG有功功率是否饱和的影响，各DCr在时钟驱动下，按式（15）和（16）进行电压和频率一致性迭代，收敛得到Uave和fave，并输出给本地二级控制器进行参考电压和参考频率的修正。

其中，n″为下垂控制 DG 数目；Ui［k］、 fi［k］分别为DGi在第k次迭代时的电压和频率值。

2.3 二级控制

（1）参考电压的修正。

有功功率和电压控制的本质都是对各DG的输出电压进行控制。

为输出目标有功功率，利用与实际有功功率之差进行PI调节，得到有功电压修正量δUi，P如式（17）所示。

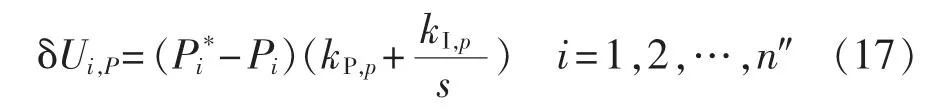
其中，kP，p、kI，p为有功电压修正中 PI控制器的参数。

一方面改进下垂控制同传统下垂控制一样不可避免地会带来电压跌落的问题，另一方面在调节有功功率的过程中，电压有可能越限。为了稳定负荷点的电压，基于Uave同步进行电压调节，产生平均电压修正量 δUi，U：

其中，g为方式选择位，当DG输出有功功率未饱和时，g=1，参与电压调节，当DG输出有功功率饱和时，输出最大有功功率，g=0，不参与电压调节；kP，u、kI，u为平均电压修正中PI控制器的参数。

下垂控制的参考电压优化为：

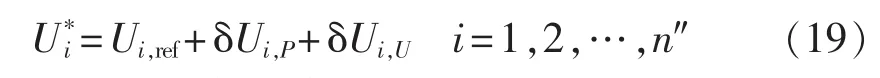
（2）参考频率的修正。

利用PI调节产生频率调节量δfi，如式（20）修正下垂控制的参考频率，通过同步频率控制，使频率稳定在额定值。

其中，kP，f、kI，f为频率修正中 PI控制器的参数。

3 算例分析

3.1 算例模型

为验证所提方法的有效性及优越性，基于MATLAB/Simulink环境建立交流微电网模型如图4所示，包括通信网络和电力网络两部分。

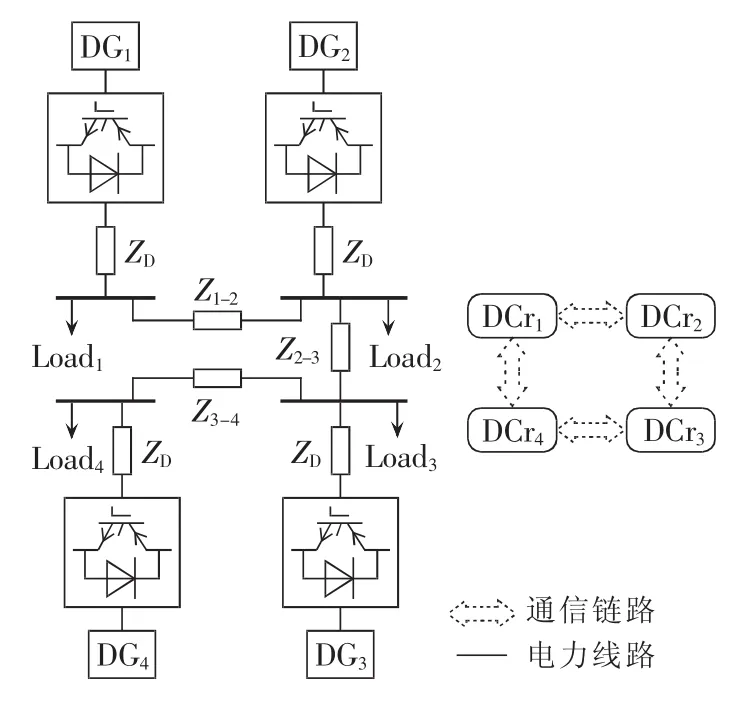
图4 微电网结构Fig.4 Structure of microgrid

微电网电压等级为380 V，系统参数如表1和表2 所示，各 DG 容量相等。 λL，P取为 1.5$/（kW·h）。DCr的时钟周期 Ts会影响系统的稳定性［15］，为了满足采样定理并提高系统的稳定性，综合实际网络特性，本文选定Ts=1 ms。

表1 系统参数表Table 1 System parameters

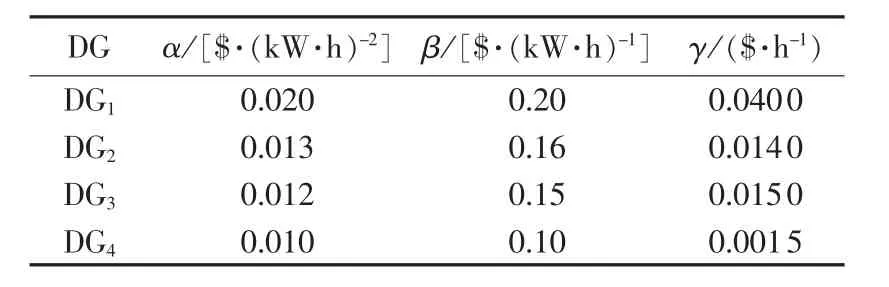
表2 各DG的成本系数Table 2 Cost coefficients of DGs

由式（12）可知一致性的收敛速度由矩阵D的λ2决定，而D由通信拓扑确定。因此，通信拓扑会影响一致性算法的收敛速度［16］。本文算例选定环网式通信拓扑，利用式（11）构造双随机矩阵D如下：

3.2 仿真结果与分析

下面通过3个仿真算例分析，将所提策略与文献［7］经济下垂控制及传统下垂控制进行对比。仿真 0.4 s时，Load1突增负荷 17+j7 kV·A，0.7 s时Load3突增负荷16+j7 kV·A。

文献［7］中无通信自治经济下垂控制，考虑各DG的运行成本，如下式：

其中λC，P为比例因子，按表 2 参数，则 λC，P取为 0.22$/h。

3.2.1 算例1：负荷变化

0～0.1s采用基于边际成本的改进控制，0.1 s后，启动分布式二级优化策略，仿真结果如图5所示。

仿真过程包含以下4个阶段。

① 0～0.1 s，由图 5（a）、（e）知改进下垂控制的功率分配精度低，各DG边际成本不一致。这是由于线路阻抗的影响，各DG未能实现边际成本相等。

②0.1 s后，启动二级优化策略，相邻DCr间进行通信，利用一致性算法得到所需信息，通过二级控制优化下垂控制的参考电压和频率。由图5（c）—（e）可看出，各DG边际成本趋于一致，全网平均电压和频率恢复至额定值。

③ 0.4 s时，由图 5（c）—（e）可看出，负荷突增导致各DG边际成本出现偏差，电压跌落，频率上升，但经过短时优化调节，系统过渡到稳定状态，仍能实现边际成本一致，平均电压和频率恢复至额定值。

④ 0.7 s时 Load3负荷突增，由图 5（a）和（e）可看出，此时系统负荷较重，成本较低的DG4输出有功功率饱和，稳定在20 kW，并退出二级优化；剩余4个未饱和DG继续参与优化策略，边际成本实现一致。

图5 各DG运行情况Fig.5 Operational conditions of DGs

此外，由于稳态时全网频率一致，图5（b）中稳态时各DG无功功率相等。

从图5（f）可看出边际成本经过13次一致性迭代，并从图 5（a）—（d）的分析可得，迭代 13次的精度可满足控制要求，系统的暂态和稳态性能较好。

图6为是否施加分布式二级优化控制的系统成本对比。可知，二级优化控制可有效地降低系统成本，这是由于其优化下垂控制的参考电压和频率，提高了下垂控制的功率分配精度。

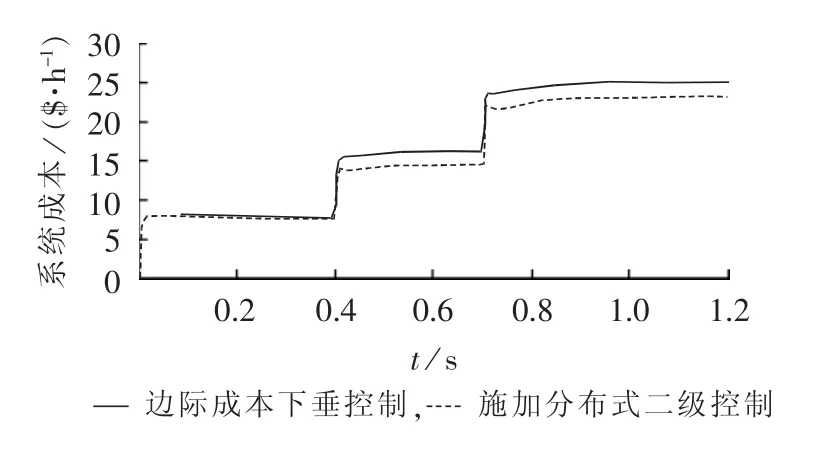
图6 所提下垂控制和分布式二级优化控制的系统成本Fig.6 System costs of proposed droop control and two-level distributed optimal control

图 7（a）、（b）分别为经济下垂控制和传统下垂控制的有功功率波形，不同方法的系统成本对比如图7（c）和表3所示。可得如下结论。

①传统下垂控制按照容量比例分配功率，但是分配精度易受线路阻抗影响。由于未考虑各DG的成本，无法经济分配功率，其系统成本最高。

图7 算例1：不同控制方法仿真结果Fig.7 Case 1：simulative results of different control strategies

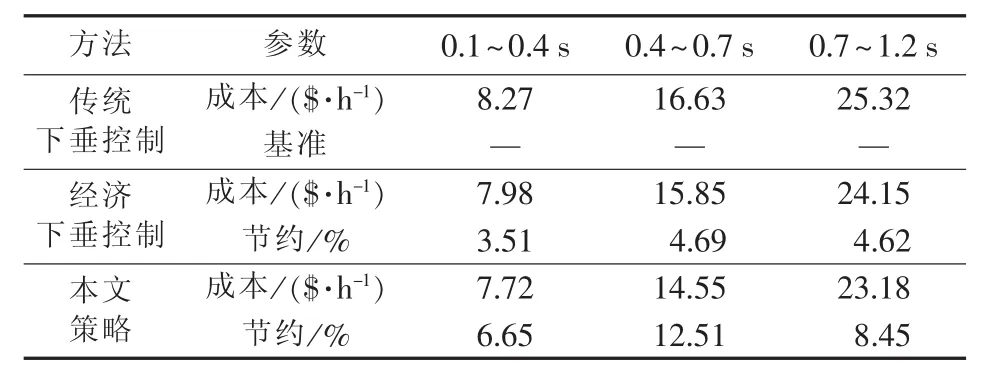
表3 3种控制下系统总运行成本对比Table 3 Comparison of total system operational cost among three control strategies

②经济下垂控制的成本居中，只在一定程度上降低系统成本。一方面，由图7（a）可看出，0.4～0.7 s时，经济下垂控制下成本较高的DG1比成本低的DG4出力大。该自治控制基于本地信息，与其他DG无信息交流，无法从全网角度优化功率分配，因此易受线路阻抗的影响，各DG不能精确按照成本大小出力，导致系统成本偏高。另一方面，经济下垂控制按运行成本大小分配出力，没有使各DG边际成本一致。

③所提策略的系统成本最低，采用基于边际成本的改进下垂控制，利用基于稀疏通信网络的分布式策略，提高下垂控制的控制精度，实现边际成本一致。0.7 s后，由于边际成本最低的DG4出力饱和，成本节约性能略有降低。

以上分析验证了所提策略能够适应负荷的变化，降低系统运行成本。

3.2.2 算例2：线路阻抗变化

将表1中的线路阻抗参数更改为Z1-2=0.1+j0.0157 Ω，Z2-3=0.2+j0.0314 Ω，Z3-4=0.3+j0.0628 Ω。3种控制方法的有功功率波形及系统成本对比如图8所示。

图 8（b）、（c）的有功功率波形与图 7（a）、（b）不同，可见线路阻抗变化对经济下垂和传统下垂控制的控制精度有较大影响。 图 8（a）与图 5（a）的有功功率波形相同，线路阻抗变化未影响所提策略的功率分配精度。由图8（d）可知，所提策略的系统成本仍最低。可见，由于采用分布式策略，通过边际成本一致优化分配全网功率，无论线路阻抗如何分布，都能有效降低系统成本。

由上述分析可得，所提策略无需测得线路阻抗的大小，便可实现控制目标，更具有适应线路阻抗变化的能力。

3.2.3 算例3：成本系数变化

将表2中DG2的成本系数改为和DG3相同，3种方法的仿真结果如图9所示。

图 9（c）与图 7（b）波形相同，由于传统下垂控制按容量比例分配功率，成本参数的变化不影响其功率分配。由9（b）与图7（a）对比知，成本参数变化影响经济下垂控制的功率分配。

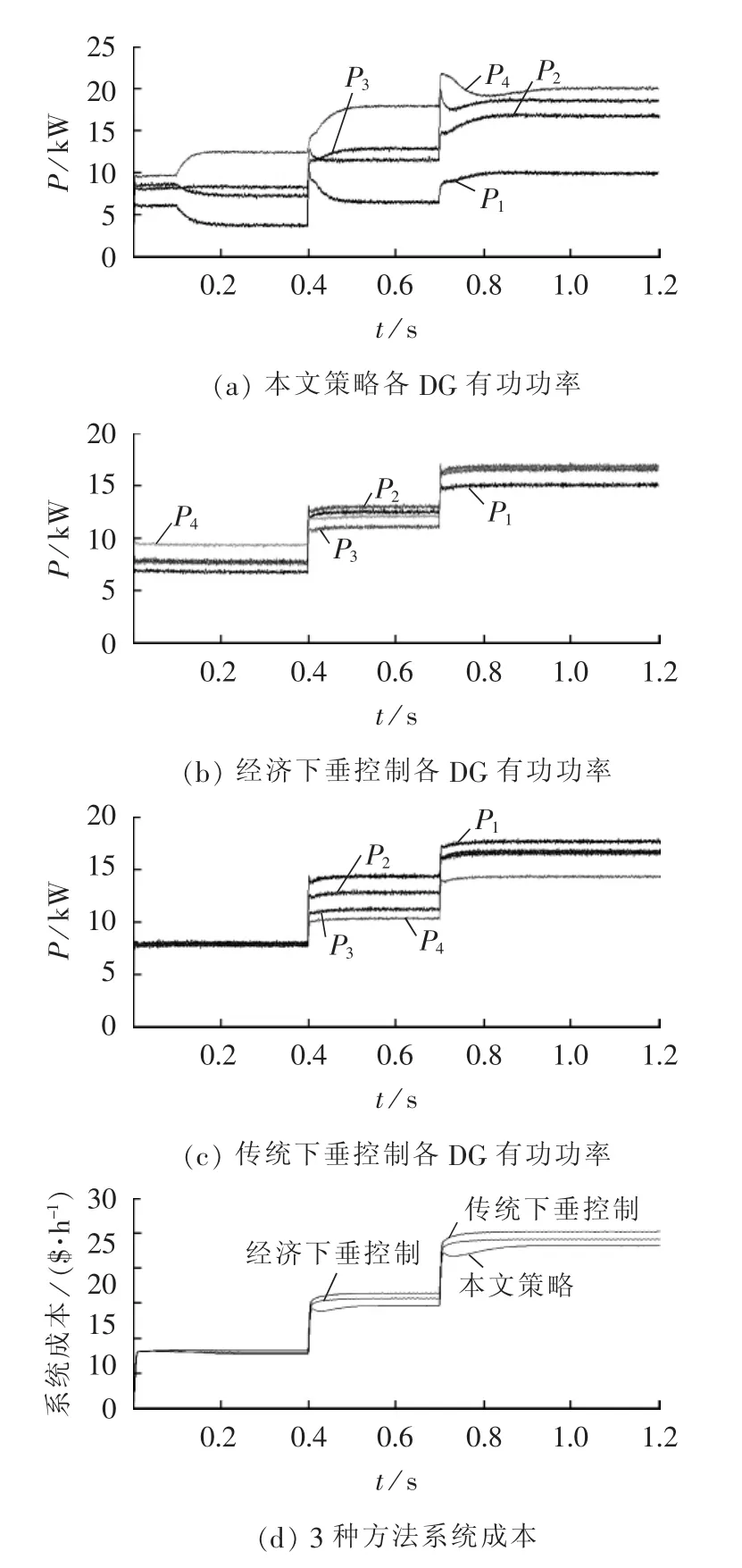
图8 算例 2：3种控制方法仿真结果Fig.8 Case 2：simulative results of three control strategies

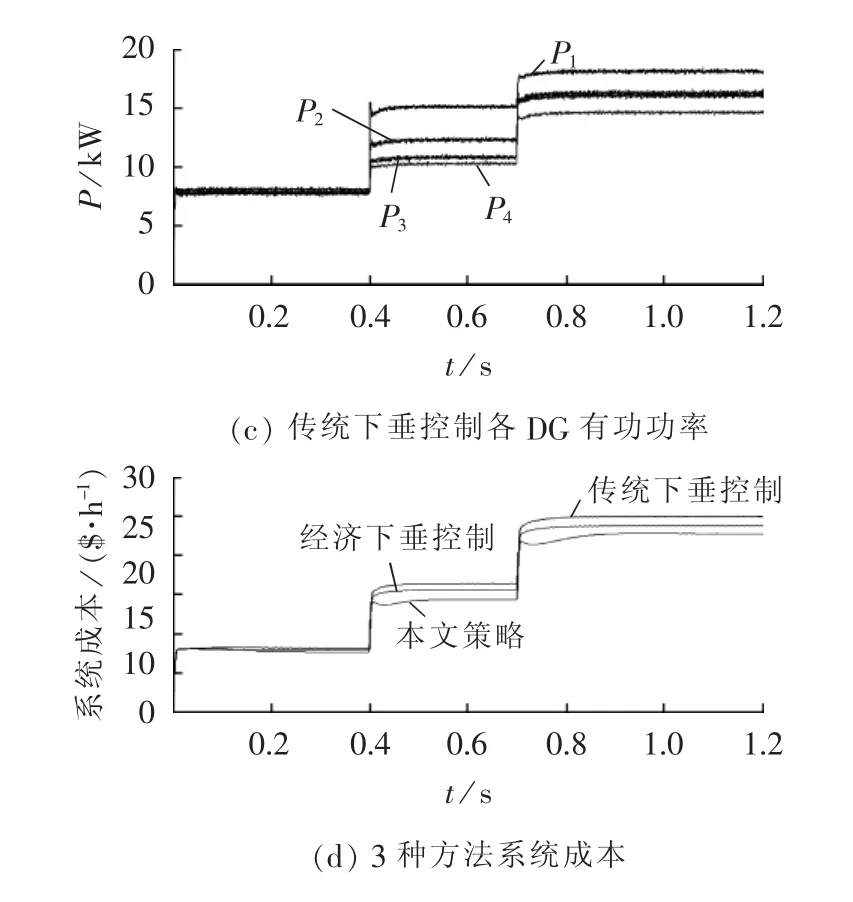
图9 算例3：3种控制方法仿真结果Fig.9 Case 3：simulative results of three control strategies

成本参数相同的DG输出有功功率应相等。从图9（b）可看出，经济下垂控制的DG2和DG3输出有功功率产生偏差，由于自治控制仅基于本地信息控制，控制精度易受线路阻抗影响。由图9（a）可看出，DG2和DG3输出有功功率相等，所提控制通过分布式策略对下垂控制进行优化调节，功率分配精度高。

从图9（d）可知，本文策略的系统成本最低，所提策略精确按照边际成本一致分配功率，有效地降低了系统成本。

4 结语

针对传统下垂控制在功率经济分配方面的不足，考虑不同类型DG运行成本的不同，本文提出基于边际成本的改进经济下垂控制。为解决其功率分配精度依赖线路阻抗的问题，提出分布式经济运行控制策略，通过相邻DG间的信息交互，利用一致性算法评估得到全局状态平均信息，从而优化分配全网功率。仿真分析表明本文策略能够适应负荷波动，无需测得线路阻抗值，便可实现各DG的边际成本一致，降低系统运行成本，微电网经济稳定运行。

［1］杨新法，苏剑，吕志鹏，等.微电网技术综述［J］.中国电机工程学报，2014，34（1）：57-70.YANG Xinfa，SU Jian，LÜ Zhipeng，et al.Overview on micro-grid technology［J］.Proceedings of the CSEE，2014，34（1）：57-70.

［2］王成山，武震，李鹏.微电网关键技术研究［J］.电工技术学报，2014（2）：1-12.WANG Chengshan，WU Zhen，LI Peng.Research on key technologies of microgrid［J］.Transactions of China Electrotechnical Society，2014（2）：1-12.

［3］ZHANG X，QSHARMA R，HE Y.Optimal energy management of a rural microgrid system using multi-objective optimization［C］∥2012 IEEE PES InnovativeSmartGrid Technologies（ISGT）.Washington DC，USA：IEEE，2012：1-8.

［4］刘春阳，王秀丽，刘世民，等.计及蓄电池使用寿命的微电网经济调度模型［J］.电力自动化设备，2015，35（10）：29-35.LIU Chunyang，WANG Xiuli，LIU Shimin，et al. Economic dispatch model considering battery lifetime for microgrid ［J］.Electric Powcr Automation Equipment，2015，35（10）：29-35.

［5］CHEN C.Economic dispatch using simplified personalbest oriented particleswarm optimizer［C］∥Electric Utility Deregulation and Restructuring and Power Technologies.Nanjing，China：IEEE，2008：572-576.

［6］ZHANG P X，ZHAO B，CAO Y J，et al.A novel multi-objective genetic algorithm for economic power dispatch［C］∥Universities Power Engineering Conference.Bristol，UK：IEEE，2004，422-426.

［7］NUTKANI I U，LOH P C，BLAABJERG F.Droop scheme with consideration of operating costs［J］.IEEE Transactions on Power Electronics，2014，29（3）：1047-1052.

［8］NUTKANI I U，LOH P C，WANG P，et al.Autonomous droop scheme with reduced generation cost［J］.IEEE Transactions on Industrial Electronics，2014，61（12）：6803-6811.

［9］NUTKANI I U，LOH P C，BLAABJERG F.Cost-based droop scheme with lower generation costs for microgrids［J］.IET Power Electronics，2014，7（5）：1171-1180.

［10］NUTKANI I U，WANG P，LOH P C，et al.Cost-based droop scheme for DC microgrid［C］∥2014 IEEE Energy Conversion Congress and Exposition（ECCE）.Pittsburgh，PA，USA：IEEE，2014：765-769.

［11］XIN H，ZHANG L，WANG Z，etal.Controlofisland AC microgrids using a fully distributed approach ［J］.IEEE Transactions on Smart Grid，2015，6（2）：943-945.

［12］ZHANG Z，YING Z，CHOW M Y.Decentralizing the economic dispatch problem using a two-level incremental cost consensus algorithm in asmartgrid environment［C］∥North American Power Symposium（NAPS）.Boston，MA，USA：IEEE，2011：1-7.

［13］LAAKSONEN H，SAARIP，KOMULAINEN R.Voltageand frequency control of inverter based weak LV network microgrid［C］∥2005 International Conference on Future Power Systems.Amsterdam，Holland：IEEE，2005：1-6.

［14］XU Y，LIU W.Novelmulti-agent based load restoration algorithm for microgrids［J］.IEEE Transactions on Smart Grid，2011，2（1）：152-161.

［15］YING X，CHOW M Y.Sampling rate selection influences on incremental cost consensus algorithm in decentralized economic dispatch［C］∥IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society.Montreal，QC，Canada：IEEE，2012：1410-1415.

［16］ZHANG Z，CHOW M Y.Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid［J］.IEEE Transactions on Power Systems，2012，27（4）：1761-1768.