基于压缩感知的人群密度估计方法研究

李　冲，　王　蓉，　陈　鹏

(中国人民公安大学警务信息工程学院， 北京　100038)



基于压缩感知的人群密度估计方法研究

李冲，王蓉，陈鹏

(中国人民公安大学警务信息工程学院， 北京100038)

摘要实时监测人群密度是预防群体性事件的有效手段之一。针对较高密度人群，提出一种基于压缩感知的人群密度估计方法。首先，利用离散余弦变换和随机高斯矩阵获取压缩感知测量值；然后利用主成分分析进行降维处理，得到人群密度特征；最后利用支持向量机将人群密度分为中、高、很高3类。通过某中学校门口的视频图像进行仿真实验，测试、比较、分析了该方法与经典的基于纹理方法的实时性与准确性。

关键词人群密度估计； 压缩感知； 主成分分析； 支持向量机

0引言

群体性事件以及人群拥挤往往会危及人的生命安全，一旦发生事故就会造成很大损失。但是，仅仅依靠传统的人防及技防手段并不能实现对人群全方位、不间断的监管。随着视频监控系统的普及和视频分析技术的发展，利用人群密度估计技术实时监测人群密度，及时发现高密度人群并报警，是实现有效预警的手段之一。

压缩感知(Compressing Sense，CS)是2006年提出的一种新采样理论，在信号满足稀疏性的条件下，对信号的高概率精确重构仅需要远少于信号维数的测量值即可完成[1-4]，在数据存储及实时处理方面均具有优势，在图像处理领域得到了广泛的研究和应用，如背景分割[5]、图像检索[6]、图像融合[7]等。

基于像素和基于纹理是两种经典的人群密度估计方法。基于像素的方法由Davies等人[8]首次提出，计算简单，但不适用于估计较高密度人群。基于纹理的方法由Marana等人[9]首次提出，以灰度共生矩阵统计值为人群密度特征，在较高密度人群情况下具有较高的准确率。由于基于像素的方法准确度较低，目前很多学者以文献[9]中基于灰度共生矩阵的方法为基础开展研究，如张文倩[10]将分形维数和灰度共生矩阵相结合，所提取的人群密度特征包括水平、垂直两个方向上灰度共生矩阵的能量、熵、对比度、逆差距8个统计量以及1个分形维数；刘小锐等人[11]结合二维快速傅里叶变换与灰度共生矩阵，将图像经快速傅里叶变换后的幅度谱看做纹理图像，提取其灰度共生矩阵特征；唐清等人[12]将模糊集理论与BP(Back Propagation)神经网络相结合，通过灰度共生矩阵特征估计人群密度。

上述基于纹理的方法虽然提高了较高密度人群的估计准确性，但由于灰度共生矩阵的计算量较大，其实时性还有待提高。为了改善基于纹理方法的实时性，本文结合压缩感知理论和主成分分析法(Principal Component Analysis，PCA)进行人群密度估计，这主要是基于以下3方面的考虑：第一，压缩感知测量值含有丰富的原始图像信息，能够表征人群密度特征；第二，压缩感知测量值的维度远少于原始信号的维度，减少人群密度特征提取的计算量，算法复杂度较低，能够缩短人群密度特征提取时间；第三，采用主成分分析法对压缩感知测量值做降维处理，降低人群密度特征向量的维度，能够缩短人群密度分类时间。

本文提出的基于压缩感知的人群密度估计方法首先利用DCT(Discrete Cosine Transform，离散余弦变换)和随机高斯矩阵获取压缩感知测量值；然后利用主成分分析进行降维处理，得到人群密度特征向量；最后利用SVM(Support Vector Machines，支持向量机)进行人群密度估计。与文献[9]中基于灰度共生矩阵的方法及文献[10]中基于灰度共生矩阵和分形维数的方法相比，本文提出的方法在实时性和准确率方面均有较大提高。

1基础理论

压缩感知是由E. J. Candes[1]、J. Romber[2]、T. Tao[3]和David L. Donoho[4]等人提出的新采样理论。在信号满足稀疏性的条件下，利用远少于原始信号维数的测量值完成信号的高概率精确重构，关键步骤包括稀疏表示、信号测量和信号重构。

1.1稀疏表示

稀疏性是压缩感知的前提，有两种方式。第一种方式，对于一维离散信号x∈RN，当其元素xi,i∈[1,N]中非零个数为k(k≪N)时，称信号x本身具有稀疏性。第二种方式，将信号x表示为某个正交基Ψ∈RN×N的线性组合形式，如式(1)所示，

x=Ψs

(1)

其中，s∈RN是x的变换系数向量，即x的等价表示，当s中仅有k(k≪N)个值非零时，称信号x在Ψ域下具有稀疏性，s即为x的k稀疏表示，Ψ为x的稀疏基[3]。

从图像的角度来说，稀疏性可以理解为像素灰度取值中含有大量的零值或近似零值，即少量的非零值即可有效表示原始图像的信息。对于自然界图像而言，除了二值图像本身是稀疏信号外，很多图像本身并不具备稀疏性，因此需要寻找合适的稀疏基将图像映射为稀疏信号。

1.2信号测量

信号测量是利用测量矩阵将稀疏信号映射到低维空间获取测量值的过程，如式(2)所示。

y=Φx=ΦΨs

(2)

其中，Φ∈RM×N(M≪N)为测量矩阵，测量值y∈RM。

Candes等人[3]的研究表明，当测量矩阵Φ满足如式(3)所示的RIP(Restricted Isometry Property)准则时，测量值y即包含重构原始信号的足够信息，

(3)

其中，ε>0，v为任意严格k稀疏的矢量。但是直接判断矩阵是否满足RIP条件很困难，Baraniuk表明，测量矩阵Φ与稀疏基Ψ不相关是RIP的一个近似等价条件[13]，实际操作中常利用该等价条件选择测量矩阵。

由于随机高斯矩阵与绝大多数稀疏基均不相关，常用于压缩感知中的测量矩阵。随机高斯矩阵Φ∈Rm×n的各元素均服从正态分布，如式(4)所示。

(4)

1.3信号重构

信号重构首先通过最小l0范数下的优化问题求式(2)的最佳稀疏解s，如式(5)所示，

min‖s‖0,y=Φx=ΦΨs

(5)

然后通过式(1)由稀疏信号s恢复出原始信号x。

由于测量值y的维度M远小于原始信号x的维度N，因此，求解式(2)的最佳稀疏解s是一个NP(Non-deterministicpolynomial)难问题。Donoho等人[14]表明，当测量矩阵满足RIP准则时，可通过求解最小l1范数问题重构信号，成为实际求解原始信号的理论依据。

2基于压缩感知的人群密度估计方法

本文所提方法的流程如图1所示，人群密度特征提取和人群密度估计是两个关键环节。

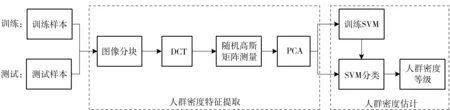
图1　基于压缩感知的人群密度估计方法流程图

2.1人群密度特征提取

本文利用压缩感知测量值表征人群密度特征，并结合主成分分析法进一步降低信号维度，最终得到6D(Dimension)人群密度特征向量。如图1所示，人群密度特征是训练支持向量机的输入向量，具体计算过程如下。

2.1.1图像分块

将原始图像划分为8×8像素大小的子图像。一般图像都具有较强的局部相关性，因此将图像划分为8×8像素的子图像能够保持图像的空间相关性；同时，8×8像素的子图像由于相关性强，变化平缓，含有的空间频率较低，因此，在经过DCT等图像变换后，其能量主要集中在少数几个系数上，有利于图像的稀疏表示。

2.1.2稀疏表示

首先，对每一个子图像执行DCT变换，得到大小为8×8的DCT变换系数。DCT变换系数反映了图像的不同频率成分，“左上角”为较低频率，“右下角”为较高频率。一般而言，图像的局部区域内变化缓慢，因此低频成分较多，高频成分较少，即经过DCT变换后的子图像能量主要集中于“左上角”的低频部分。因此，DCT变换系数在“左上角”位置处的数值较大，越往“右下角”方向数值越接近于零。然后，对DCT变换系数进行量化。量化是对DCT变换系数进行压缩和取整的过程，经过量化后，DCT变换系数中的零值个数增多，即可得到稀疏子图像。量化过程如式(6)所示。

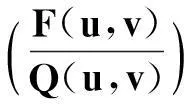
(6)

其中，F(u,v)为DCT变换系数，Q(u,v)为量化步长，Fq(u,v)为量化后的DCT系数。

人眼对不同频率分量对应图像的敏感度和分辨能力不同，一般对低频分量较为敏感，因此，常采用不同的量化步长对DCT变换系数进行量化，以更好地符合人眼对图像的主观感受。表1是JPEG标准采用的亮度量化步长，本文据此对DCT变换系数进行量化。

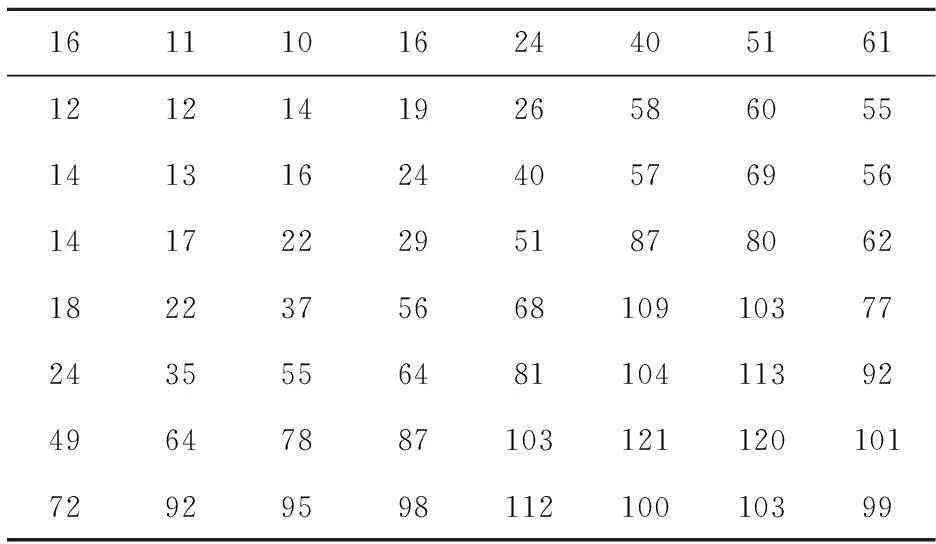
表1　JPEG标准亮度量化表

最后，将量化后的DCT系数转换为长度为64的1D信号，得到稀疏信号。

2.1.3信号测量

文献[15]通过一系列实验比较分析了不同采样率下信号重构效果的好坏，结果表明，当采样率为30%时即可满足精确恢复原始信号的要求。因此，本文将采样率设为31.25%，构造大小为20×64的随机高斯矩阵作为测量矩阵，获取长度为20的测量值；

重复上述图像分块、稀疏表示、信号测量的步骤，得到所有子图像的测量值，并转换为1D信号。

2.1.4主成分分析

对压缩感知测量值进行主成分分析，所保留的主成分个数即为人群密度特征向量的维数。特征向量维数越低，计算越简单，实时性越好，但同时也可能会降低识别准确性。为了均衡准确性和实时性，本文分别计算了不同特征向量维数下基于压缩感知的人群密度估计方法的准确性和实时性。

特征向量维数范围设定为2～20D，分别计算每种向量维数下人群密度估计的准确性和实时性。其中，准确性由100幅测试图像中正确分类图像所占比例衡量，结果如图2所示；实时性由单幅图像的人群密度特征提取时间衡量，结果如图3所示。

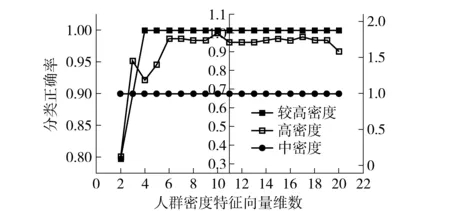
图2　不同特征向量维数下的正确率

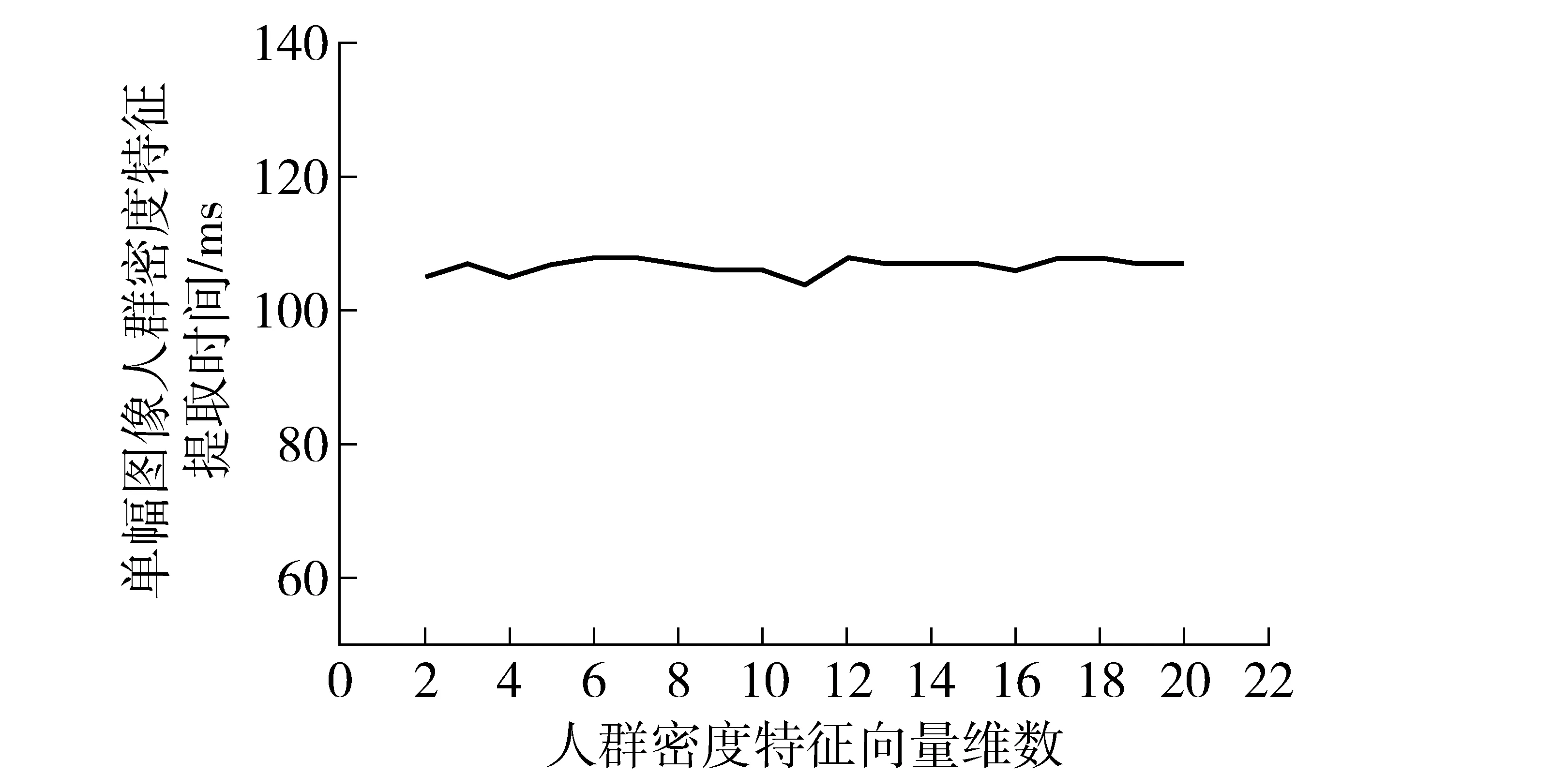
图3　不同特征向量维数下的实时性

由图2可知，当特征向量维数低于6D时，随着维数的提高分类正确率总体呈上升趋势；当特征向量维数高于6D时，分类正确率处于稳定状态，且均在95%以上，能够满足人群密度估计要求。因此，当特征向量维数大于6时，本文方法能够满足准确性要求。

由图3可知，当特征向量维数从2～20D变化时，单幅图像的特征提取时间变化范围在5 ms以内。这是因为，人群密度特征提取时间包括获取测量值和主成分映射两部分，其中，前者占据绝大部分时间，后者约为1 ms。因此，特征向量的维数在小范围内变动时，对本文方法的实时性影响不大。

基于上述分析，确定人群密度特征向量的维数为6D，即保留主成分分析的前6个主成分，构成人群密度特征向量。

2.2人群密度分类

本文选择SVM实现人群密度分类。SVM是一种监督式学习方法，解决在原始空间中线性不可分的非线性分类问题，能够在小样本情况下取得较好的分类效果，但不能直接用于多类别的分类。

为实现中、高、很高3种密度等级的分类，本文采取“投票法”策略[16]，首先，由3个SVM构造二级分类器，如图4所示，其中第一级为SVMa，实现中、很高类别分类，SVMb和SVMc处于第二级，分别实现中、高、很高三个类别的分类。

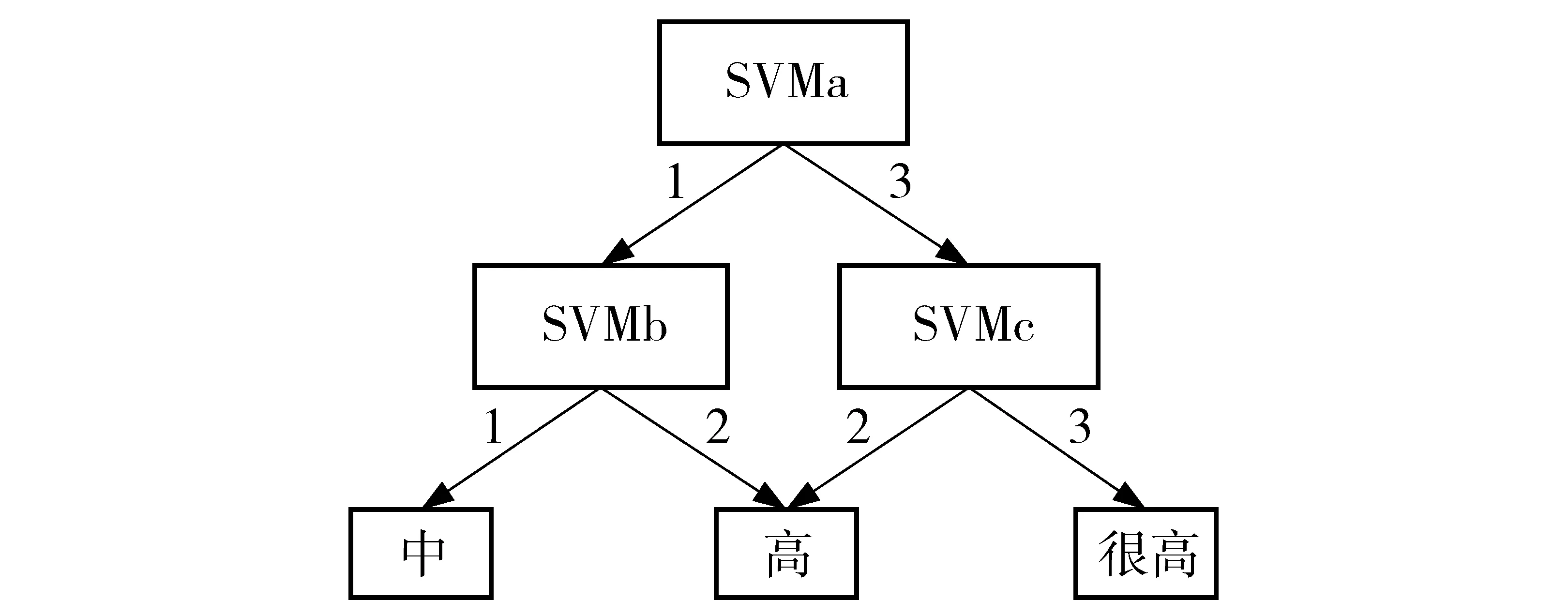
图4　SVM结构

2.3仿真实验与结果分析

2.3.1仿真实验图像

本文仿真实验的视频来自于某中学校门口的一段监控视频，其真实场景面积约为10 m2，图像大小为320×240。根据表2所示Polus提出的人群密度等级的定义[17]，针对较高密度人群，仿真实验将人群密度等级划分为中、高、很高3类，如表3所示。

以15帧为间隔抽取该监控视频图像750帧，用于仿真实验。其中，训练图像共450帧，中、高、很高

密度各150帧；测试图像共300帧，中、高、很高密度各100帧。各密度等级的示例图像如图5所示。

表2　Polus人群密度等级定义

表3　本文人群密度等级划分

图5　不同人群密度等级图像示例

2.3.2仿真实验环境

仿真实验的软件环境主要包括Visual Studio 2010、SQL Server2012、Qt Creator5.2.0、OpenCV2.4.8；硬件环境为Inter(R) Core(TM) i5-2450M CPU。

2.3.3实验结果及分析

为了验证本文所提方法的有效性，对本文方法、文献[9]中基于灰度共生矩阵的方法、文献[10]中基于灰度共生矩阵和分形维数的方法均进行了仿真实验，并比较分析其实时性和准确率，分别如表4和表5所示。

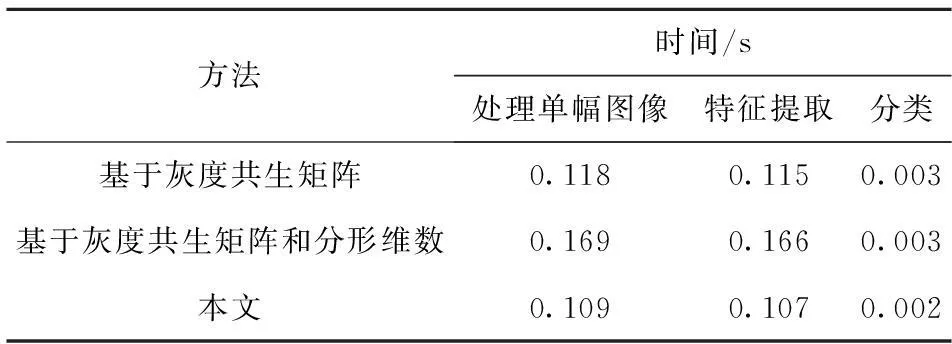
表4　实时性分析

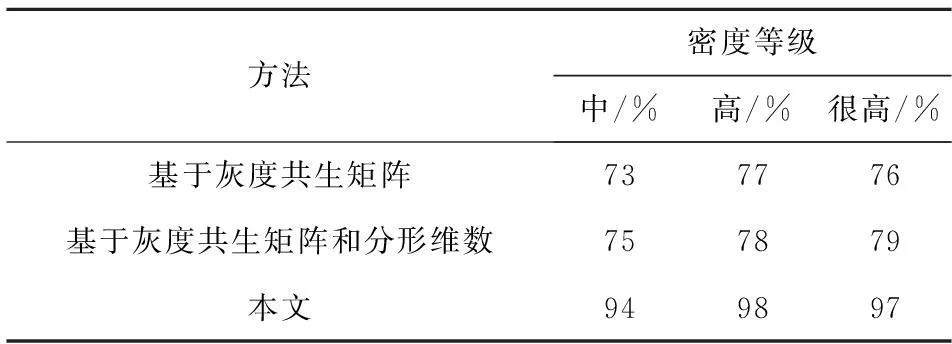
表5　准确率分析

由表4可知，本文方法的特征提取时间少于基于灰度共生矩阵的方法和基于灰度共生矩阵以及分形维数的方法；同时，人群特征向量仅为6D，分类耗时较低，实时性最好。基于灰度共生矩阵和分形维数的方法由于增加了对分形维数的计算过程，所需的特征提取时间大于基于灰度共生矩阵的方法和本文方法。

由表5可知，与基于灰度共生矩阵的方法和基于灰度共生矩阵和分形维数的方法相比，本文方法的准确率有很大提高，这是因为压缩感知测量值包含丰富的原始信息，能够准确表述图像特征。

3结论

实时监测人群密度，及时发现拥挤人群，是辅助群体性事件预警的一种有效手段。针对较高密度人群，本文提出了一种基于压缩感知的人群密度估计方法。通过某中学校门口的视频图像进行了仿真实验，结果表明，本文方法与基于灰度共生矩阵的方法，以及基于灰度共生矩阵和分形维数的方法相比，在准确率和实时性方面均占有优势。随着人群密度估计技术的研究和发展，该技术将在智能视频分析领域发挥更加重要的作用。

参考文献

[1]Candes E. Compressive sampling[A]. Proceedings of the International Congress of Mathematicians[C]∥Proceedings of the Intemational Congress of Mathematicans, 2006(3):1433-1452.

[2]Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans. on Information Theory, 2006, 52(2):489-509.

[3]Candes E, Tao T. Near optimal signal recovery from random projections: Universal encoding strategies[J]. IEEE Trans. Info. Theory, 2006, 52(12): 5406-5425.

[4]David L. Donoho. Compressed sensing[J]. IEEE Transaction on Information Theory, 2006, 52(4): 1289-1306.

[5]李杰,程旺宗. 基于压缩传感的背景差分方法研究[J]. 数字社区&智能家居, 2010(2):410-412.

[6]周燕,曾凡智,卢炎生,周月霞. 基于压缩感知的图像检索方法研究[J]. 中山大学学报：自然科学版, 2014, 53(1):57-62,66.

[7]Tao W, Nishan C, Alin A. Compressive Image Fusion[J]. In: Proc of IEEE Int Conf on Image Processing. California, 2008:1308-1311.

[8]Davies A C, Jia Hong Yin Velastin, S A. Crowd monitoring using image processing[J]. IEEE Electronics & Communication Engineering Journal, 1995,7(1):37-47.

[9]Marana A N, Velastin S A, Costa L F, et al. Automatic estimation of crowd density using texture [J]. Safety Science, 1998, 28(3): 165-175.

[10]张文倩. 基于灰度共生矩阵和分形的人群密度估计[J]. 电子测试, 2012(5):36-39,45.

[11]刘小锐,周激流,李晓华. 频域基于灰度共生矩阵的人群密度估计[J]. 微计算机信息, 2008,24(34):310-311,314.

[12]唐清, 王知衍, 严和平, 等. 基于模糊神经网络的大场景人群密度估计方法[J]. 计算机应用研究,2010,27(3):989-991.

[13]Baraniuk R. A lecture on compressive sensing [J]. IEEE Signal/Processing Magazine, 2007, 24(4): 118-121.

[14]Donoho D L, Elad M, Temlyakov V N. Stable recovery of sparse over complete representations in the presence of noise[J]. IEEE Transactions on Information Theory, 2006, 52(1): 6-18．

[15]Liu L, P. Fieguth, Texture classification from random features[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 574-586.

[16]刘志刚,李德仁,秦前清,等. 支持向量机在多类分类问题中的推广[J]. 计算机工程与应用, 2004, 40(7):10-13,65.

[17]Schofer J, Ushpiz A, Polus A. Pedestrian flow and level of service[J]. J. Transportation Eng, 1983, 109(1): 46-56.

(责任编辑于瑞华)

中图分类号D035.33

作者简介李冲(1992—)，女，河南周口人，2013级在读硕士研究生。研究方向为数字图像处理、模式识别。

基金项目国家自然基金(71203229)项目；2014北京市支持中央高校共建项目公安视听专业建设项目；中国人民公安大学2015年中央高校基本科研业务费专项资金资助项目(2015JKF01243)。