三维非线性弹性壳体的维数分裂法∗

章 胤, 李开泰

(1-西安交通大学数学与统计学院，西安 710049;2-燕山大学理学院，秦皇岛 066004)

1 引言

弹性壳体和板的理论是弹性理论中最重要的课题之一，也是现代工程中最重要的课题之一．例如，它出现在火箭、导弹、航空航天飞行器、汽车、高速火车、轮船和舰艇等等装备中．关于线性和非线性弹性壳体的渐近分析和维数分裂方法以及连续介质力学的维数分裂方法可见李开泰和黄艾香的著作以及他们相关的文献[1–6]中．在Love的原创性的工作以后，苏联学者们也做了大量的经典工作，如Vlasov[7]，Norovich[8]等．壳体理论的近代发展，表现在Koiter[9,10]，Naghdi[11,12]中．关于非线性弹性力学的数学理论，如数学描述和解的存在性证明，可参见Ball[13]，Marsden和Hughes[14]，Ciarlet[15,16]等经典著作．关于线性弹性壳体的渐近分析的经典著作是Ciarlet[17]和他的学生的合作研究文献．

经典的线性壳体的渐近分析方法是，用一个2D-3C(二维三个分量)变分问题来逼近三维线性壳体问题

其中2ε是壳体的厚度，ζ=(ζi,i=1,2,3)为定义在壳体中性面ℑ上的二维向量，LM定义在二维流形上的膜算子，LB定义在二维流形上的弯曲算子，L(η)定义在二维流形上的外力算子，中性面ℑ附近的位移向量u(x1,x2,x3)用下列向量来逼近

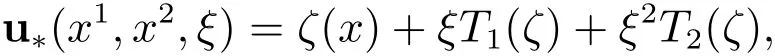
其中x=(x1,x2),x3= ξε,T1,T2为两个光滑函数．例如Koiter[9]、Na-ghdi[11]、Ciarlet[17]和李开泰[4]等都有这方面的工作．

本文给出了一个建立在半测地坐标系下的非线性弹性壳体的维数分裂方法，它把一个非线性弹性算子分裂为一个称为膜弹性算子和弯曲弹性算子之和．假设非线性弹性壳体的解可以展开为关于贯裁变量的Taylor级数，那么本文给出关于首项的一个2D-3C非线性偏微分方程，证明其解的存在性，同时给出了两个关于一阶项和二阶项对于首项的函数，从而无需求解偏微分方程即可得到一阶项和二阶项．本文安排如下，第2节给出三维弹性材料的本构方程和S-坐标系，第3节给出维数分裂方法，第4节给出非线性弹性力学变分问题，在S-坐标系系下，一阶和二阶逼近模型，近似解的存在性．

2 三维弹性材料的本构方程和S-坐标系

弹性体中因反抗变形而产生的内力，用应力张量来描述．在流体运动过中，由于全压力和内摩擦也会产生一种内力，同样可用二阶应力张量来描述它，称为Cauchy应力张量，而弹性体在外力作用下发生变形，可用变形张量E来描述，Green-St.Venant应变张量E是位移向量u的函数．应力和应变是在外部原因的作用下介质内部发生的现象，他们之间存在相互依存关系．可以认为Cauchy应力是变形梯度张量的函数τ(φ(x))=Υ(x,∇φ(x))，称为Cauchy应力的响应函数，使得Cauchy应力在材料物体所占据的变形后的构形里的任一点φ(x)=x+u(x)是由它所表达的函数，那么称这样的材料为弹性材料．如果Υ不明显依赖于x，那么称这样的弹性体为齐次的，否则称为非齐次的．以下假定弹性材料是齐次，故有材料的本构方程

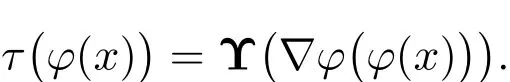
应力的响应函数是由弹性材料的性质决定的．如果f为单位质量弹性体所受的外力，ρ为弹性体的密度，那么动力学的守恒方程

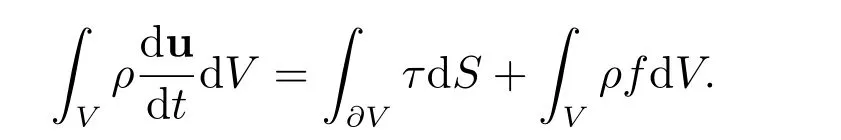
记Mn=所有n阶方阵的集合，={q|q∈M3,det(q)>0}，={所有n阶正定对称矩阵的集合}．Υ能够作为响应函数，必须满足所谓客观性假设，即对任何正交矩阵Q∈Ξ3和任何三阶方阵S∈，当且仅当成立Υ(QS)=QΥ(S)QT．一种弹性材料是各向同性的，如果对任何Q∈Ξ，响应函数满足Υ(SQ)=Υ(S),∀S∈．我们有下列关于应力和应变之间的关系的本构方程的定理：

定理1[14]对于各向同性的齐次的弹性材料，那么Cauchy应力的响应函数为

特别，当参考构形为自然状态Υ(I)=0时，则对在参考构形附近的变形，如果函数γi,i=0,1,2，在单位矩阵的主值iI=(3,3,1)处是可微的，那么本构方程可以表示为

其中A是四阶弹性系数张量．E为Green-St.Venan二阶变形张量，o(|E|)表示|E|的高阶项，而B,C为左Cauchy-Green应变张量和右Cauchy-Green应变张量，βi和γi,i=0,1,2，分别为对称张量B和C的三个主不变量IB和IC的标量函数．I为二阶单位张量，如果在(3)中忽略掉E的高阶项，满足这样本构关系的弹性材料，称为St.Venant-Kirchhoff弹性材料．它的本构方程(3)变为

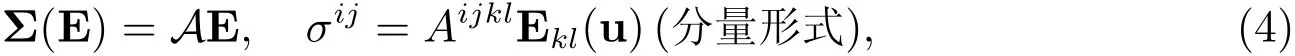
这个关系乃满足客观性假设．

St.Venant-Kirchhoff弹性材料它是一种最简单的非线性弹性材料．如果它又满足各向同性性质和齐次性，那么存在常数λ>0,µ>0，称为Lam´e常数，它们与Poisson比ν和Young氏模量E有如下关系

使得四阶弹性系数张量A的協变分量和逆变分量分别可以表示为

在以上的讨论中，所有的物理量表达的物理关系式，只有在引用坐标系之后，才能表达成数学的、可以计算的形式．设Ω⊂ℜ3中一个连通域，一个弹性体所占有的空间，{xi,i=1,2,3}是ℜ3中的一个曲线坐标系，而(gij,gij)为它的度量张量的協变分量和逆变分量，gijgjk=，对应的行列式g=det gij>0,ei,ei,i=1,2,3，分别为这个坐标系的協变基向量和共轭基向量，u(x)为在x点的位移向量u=uiei=uiei，ui,ui分别是位移向量在坐标系{xi}下的協变分量和逆变分量，并且ui=gijuj,ui=gijuj，通过指标上升和下降实现分量的转换．循环张量定义为

Gr(u)=∇u称为位移梯度张量，且位移的梯度张量Gr(u)=(∇iuj)可分解为一个二阶对称张量和一个二阶反对称张量之和

这里对称张量eij(u)是物体纯变形的度量，称它为应变张量．反对称张量cij(u)是描述物体转动，对应于一个位移向量的旋度．

对有限变形，我们可以这样来考虑．设在M点处，变形前有一个无限小向量d r0，变形后的相应向量为d r=r0+d u0，相应的弧长为

显然Eim(u)是对称的，且它是一个二阶协变张量，称它为Green-St.Venant应变张量．它是两部分之和，第一部分是线性部分，称它为关于位移向量u的应变张量，它也是对称的二阶张量．Green-St.Venant应变张量是由应变张量加上一个非线性项(u的二次齐次项)而得．

对于壳体，更为方便，取半测地坐标系．设ℑ⊂E3是一张光滑的二维曲面．令ω⊂R2是一个区域，:→E3的光滑内射，ℑ是⃗θ的映像．三维弹性壳体⊂E3是由所有与ℑ距离小于或等于ε的点组成的，2ε>0为壳体的厚度．令n记沿ℑ上连续变化的单位法向量，Ωε:=ω×(−ε,ε)．那么三维壳体是映射:→E3的映像

其中x=(xα,α=1,2)通常称为ℑ上的Gauss坐标系，而(x,ξ)称为建立在ℑ上的半测地坐标系(Semi-geodesic coordinate system，如果E3是Riemann空间，那么ℑ是二维流形)简记为S-坐标系．

往后，Latin指标和上、下标：(i,j,k,···)取值{1,2,3}，而Greek指标和上、下标：(α,β,γ,···)取值{1,2}．另外，Einstein’s求和约定：上下指标相同表示求和．曲面ℑ的度量张量的协变分量和逆变分量aαβ=,aαβaβλ=，其中=，而第二和第三基本型张量的协变分量

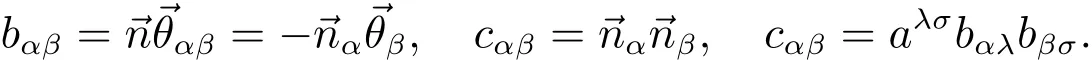
相应的逆变分量bαβ,cαβ和逆矩阵ˆbαβ,b cαβ为

在S-坐标系下，三维欧氏空间的度量张量可以表示为贯截变量ξ的多项式，其系数是曲面ℑ度量张量，第一、第二基本型张量的函数

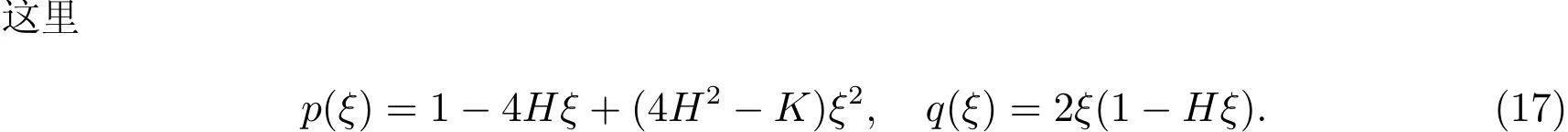
特别地，对gαβ做关于ξ的Taylor展开

空间E3和曲面ℑ的协变导数

3 三维非线性弹性壳体的维数分裂方法

我们知道三维非线性弹性壳体的边值问题是求u=(ui):Ω→ℜ3，使其满足

其中，应力张量σij，第二Piola-Kirchhoff应力张量Σij和第一Piola-Kirchhoff应力张量u)由下面给出

因为σij和Σij可以展成Taylor级数，则eΣ(u)也允许展成关于贯截变量ξ的如下形式

定理2 由(27)所定义的非线性弹性算子可以展成关于贯截变量ξ的级数

4 相应的变分问题

假设非线性弹性材料是St.Venant-Kirchhoff材料，则其位移向量场u应满足下列极小值问题

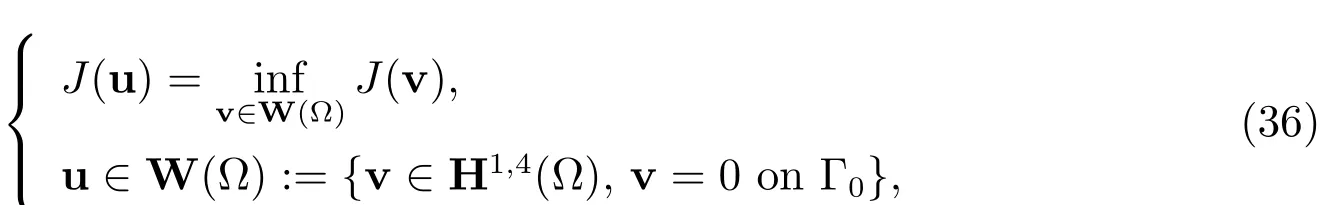
其中目标泛函

同时，(u)∈ L(W1,4(Ω);L2(Ω))是映射Eij:W1,4(Ω)→ L2(Ω)在任意点u ∈ W1,4(Ω)的Frechet导数．从而一个位移u∈W(Ω)是能量泛函J的驻点(临界点)，即u满足J′(u)=0，如果仅仅求u∈W(Ω),∀v∈W(Ω)，使得

其中Eij,Fij是贯截变量ξ的二次多项式

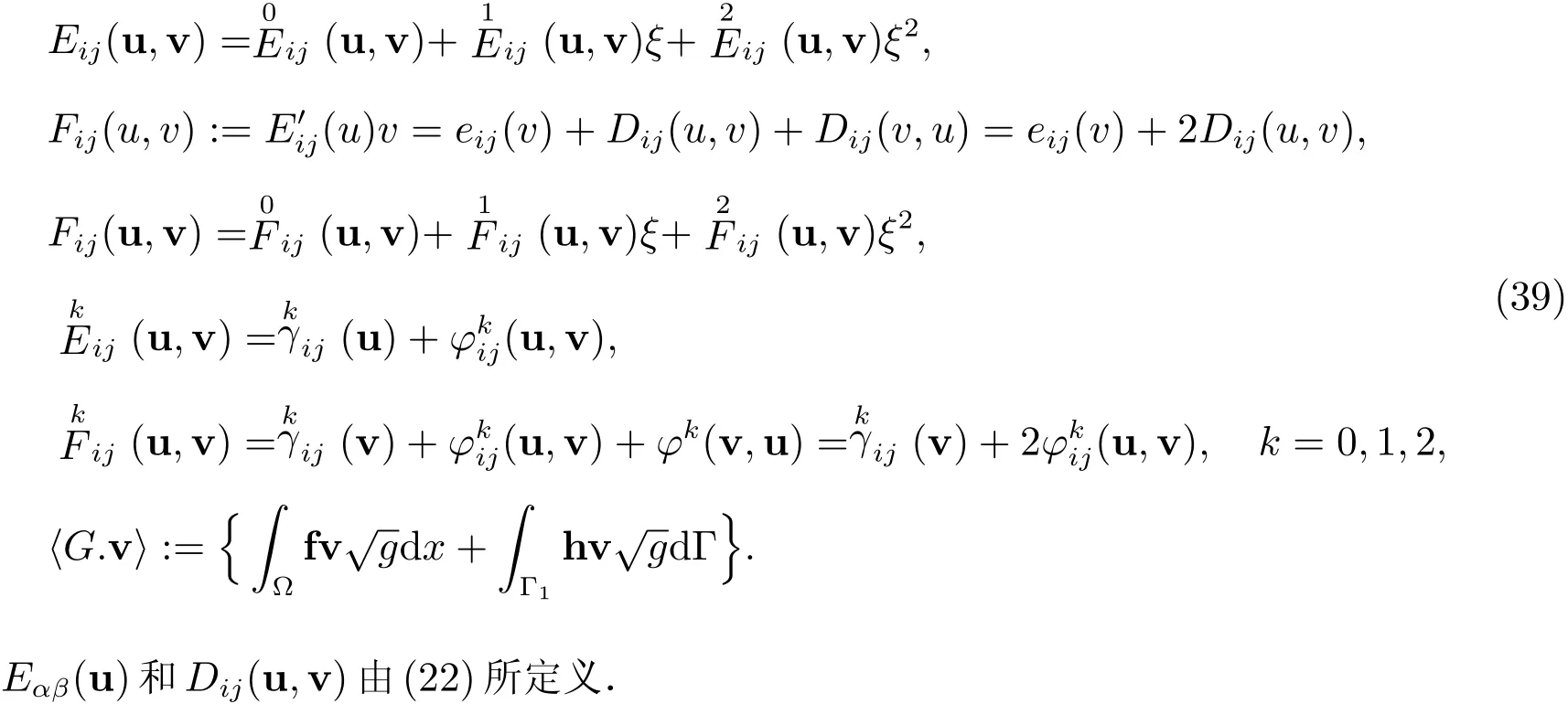
引理2 在S-坐标系下，假设极值问题(36)的解u可以有Taylor展式

下面我们分别研究变分问题的一阶截断的变分问题P1(ω)：设

4.1 变分问题P1(ω)

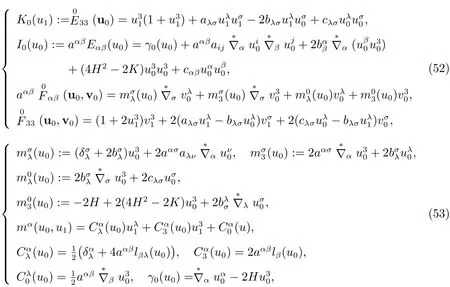
这里lαβ,lα由(26)所定义．

定理3 假设变分问题(38)的解u，作用在壳体的体积力和面力G允许有关于贯截变量ξ的Taylor展式．设u0,u1是一阶裁断变分问题(46)的解，那么：

(I) u0是下列变分问题的解，求(u0)∈W(ω),∀v∈V(ω)，使得

(III) u0也是下列边值问题的解

其中中性面上切空间的应力张量和张量分别为

这就是(54)．由(56)所定义的泛函J是光滑的，并且从(37)可知它的梯度方程是(57)，它的解是相应J的极小值问题的临界点．极小问题解的存在性后面证明．

下面我们证明，如果u0是变分问题(54)的解，并且足够光滑，那么它也一定满足边值问题(58)．实际上，由(55)，可得

从而可以得到下列对应的边值问题

这就得到(56)，下面我们可以将(56)分离出线性部分．注意到

下面我们计算导数

应用求导顺序对调的Ricci公式和Riemann曲率张量性质得因为Riemann曲率张量性质和二为流形上Ricci张量与度量张量的关系Rσλσν=Rλν=K aλν，从而有

将以上结果代入(66)，得到有显示线性算子的方程

由于检验函数,的任意性和相互独立性，由上式可得到一组三个变量uα1,u31三次多项式方程组Xi(u0,u1)=0,i=1,2,3．根据Bezout定理，它至少有一组根．从而得到函数关系u1= Π(u0)．

4.2 解的存在性

引理4 由(56)所定义的泛函J(u)在V(ω)上是强制的

这就导致矛盾，从而证明了(71)．

定理5 假设壳体中性面足够光滑，并使得aαβ,bαβ∈C2(ω)，那么极小值问题

其中K0(u0,v0)由(56)定义．

证明 由文献[15]知，假设X是一个自反的Banach空间，K是X中一个非空弱闭子集，那么如果定义在K上一个泛函f(u)是弱下半连续：

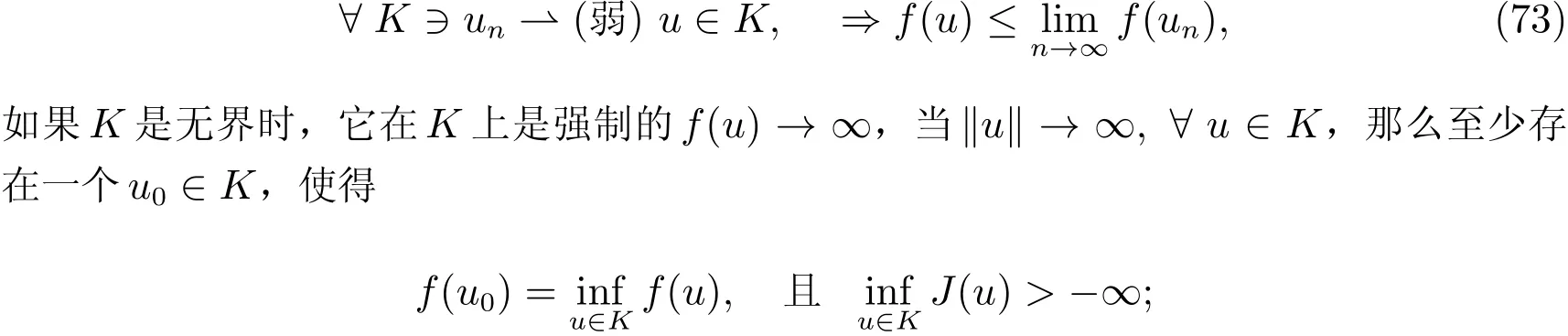
如果K=X，并且f(u)∈C1，那么f′(u0)=0,c=f(u0)是f(u)的一个临界值，f−1(c)中的任一个元素是f(u)的一个临界点．

由引理4，我们只要证明由(56)定义的泛函是弱下半连续就够．为此设序列在V中弱收敛于u0∈V:un∈V,un⇀u0∈V，那么有下面我们证明右边第二式的极限是零，那么就得到(73)．

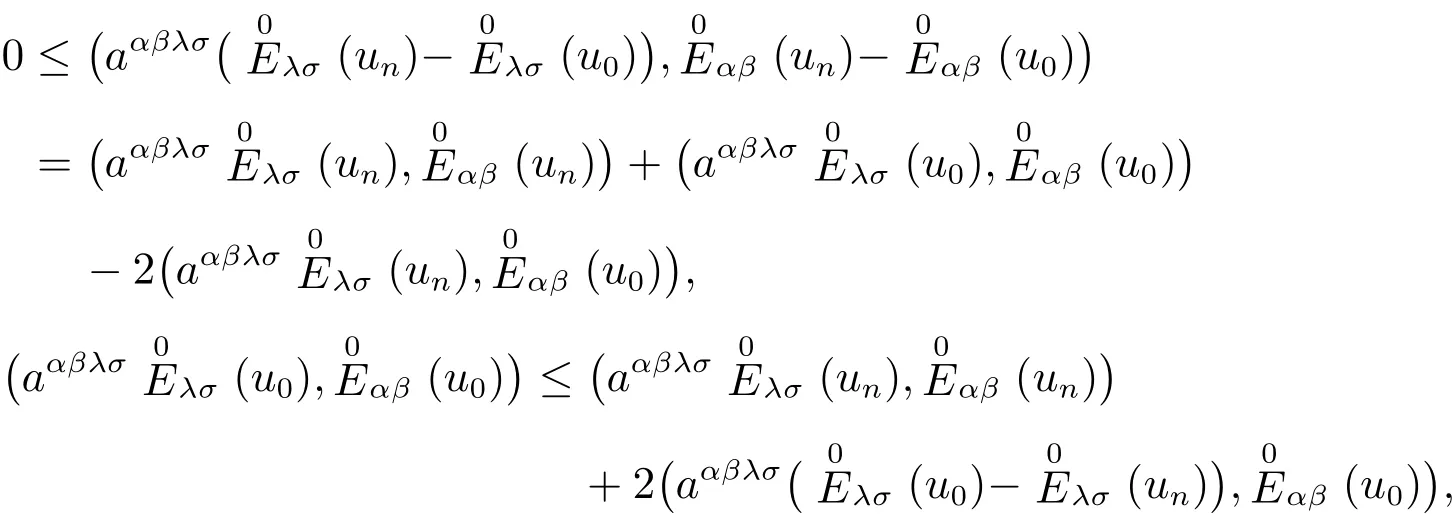
利用(37)和(39)，以及aαβλσ关于指标的对称性可得应用Green公式和边界条件，并注意度量张量的协变导数为零，则有

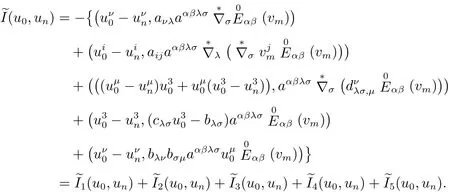
由于假设壳体中性面足够光滑，使得

因为在有界域ω上，H1(ω)y Lk(ω),k≤ 4，是紧嵌入，所以在V(ω)的弱收敛序列un在Lk(ω)中强收敛

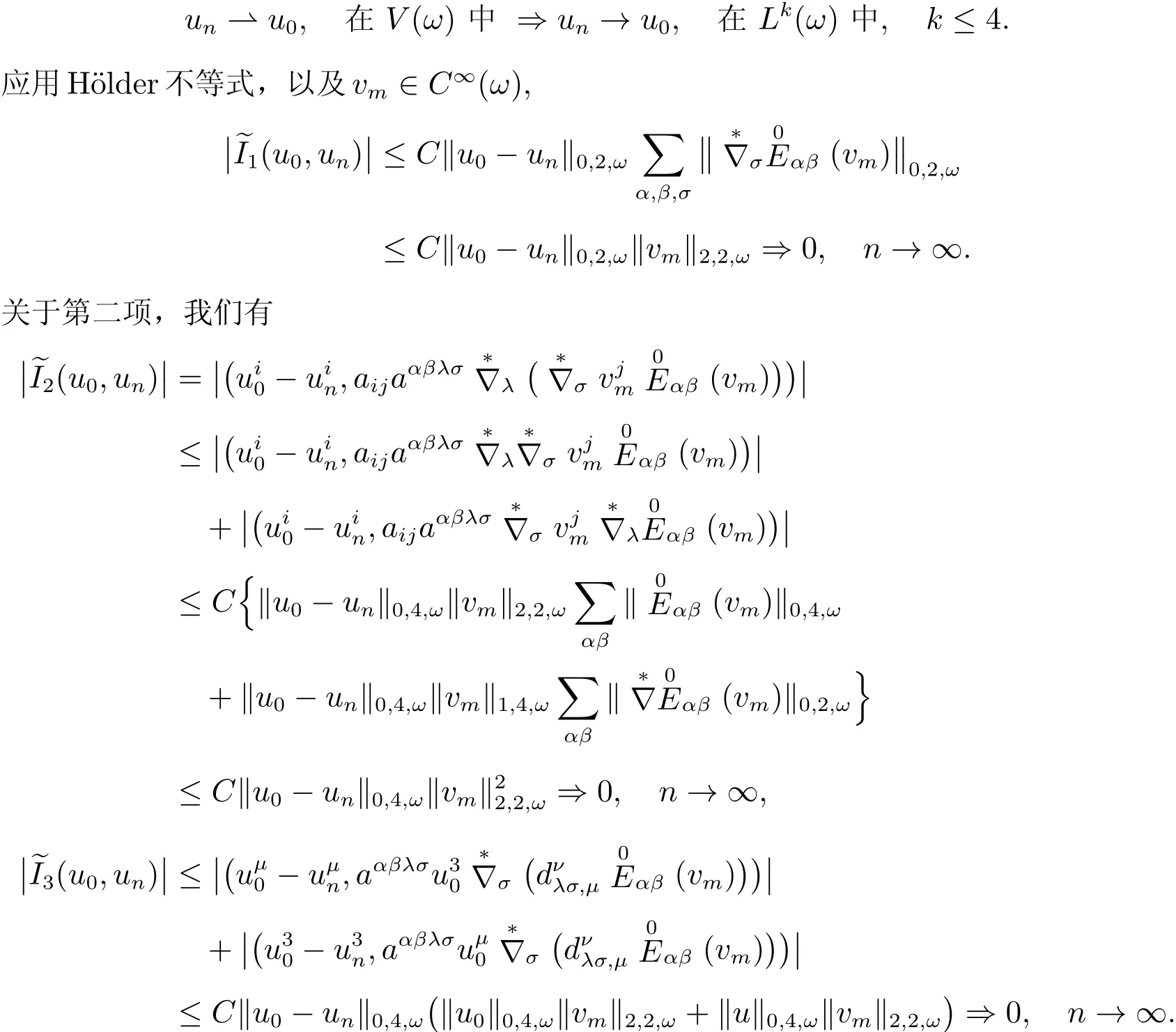
由以上讨论和C∞(ω)在V(ω)中稠密，并令m→∞，我们得到

联合(63)和(74)，定理得证．

5 变分问题P2(ω)

命题3 存在映射Π:V(ω)→L2(ω)，使得(u1,u2)=(Π1u0,Π2u0)，它是下列非线性方程组的解

由于篇幅所限，以上命题的证明从略．

参考文献：

[1]李开泰，黄艾香，黄庆怀.有限元方法及其应用[M].北京：科学出版社，2006 Li K T,Huang A X,Huang Q H.Finite Element Method and its Applications[M].Beijing:Science Press,2006

[2]Li K T,Huang A X,Huang Q H.Finite Element Method and its Applications[M].Beijing:Science Press,2015

[3]李开泰，黄艾香.张量分析极其应用[M].北京：科学出版社，2004 Li K T,Huang A X.Tensor Analysis and its Applications[M].Beijing:Science Press,2004

[4]Li K T,Zhang W L,Huang A X.An asymptotic analysis method for the linearly shell theory[J].Science in China Series A:Mathematics,2006,49(8):1009-1047

[5]Li K T,Shen X Q.A dimensional splitting method for the linearly elastic shell[J].International Journal of Computer Mathematics,2007,84(6):807-824

[6]Shen X Q,Li K T,Ming Y.Asymptotic expansions of stress tensor for linearly elastic shell[J].Applied Mathematical Modelling,2013,37(16-17):7964-7972

[7]Vlasov V Z.The basic diff eretial equations in the general theory of elastic shell[J].Mathematical Mechanics,1944,8:109-140

[8]Vorovich I I.Nonlinear Theory of Shallow Shell[M].Heidelberg:Springer-Verlage,1989

[9]Koiter W T.A consistent fi rst approximation in the general theory of thin elastic shells[C]//IUTAM Symposium on the Theory of Thin Elastic Shells,Delft,1959:12-33

[10]Koiter W T.On the foundations of the linear theory of thin elastic shells,I,II[C]//Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen Series B-Physical Sciences,1970,73(3):169-195

[11]Naghdi P M.Foundations of elastic shell theory[C]//Progress in Solid Mechanics,North-Holland,Amsterdam,1963,4:1-90

[12]Naghdi P M.The theory of shells and plates[C]//Handbuch der Physik,Springer-Verlag,Berlin,1972,2:425-640

[13]Ball J.Convexity conditions and existence theorems in nonlinear elasticity[J].Archi for Rational Mechanics and Analysis,1977,63:337-403

[14]Marsden J E,Hughes Thomas J R.Mathematical Foundations of Elasticity[M].New York:DOVER Pulications,1993

[15]Ciarlet P G.Mathematical Elasticity,Volume III:Theory of Shells[M].Amsterdam:North-Holland Publishing Company,2000

[16]Ciarlet P G.Linear and Nonlinear Functional Analysis with Applications[J].Philadelphia:SIAM,2013

[17]Ciarlet P G.Mathematical Elasticity,Volume I:Three Dimensional Elasticity[M].Amsterdam:North-Holland Publishing Company,1988