Stability of Steady States for the Holling-Tanner Predator-prey M odel with Nonlinear Boundary Conditions∗

GAO Yu,LI Yan-ling

(College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062)

1 Introduction

In this paper,we consider the following Holling-Tanner predator-prey model with nonlinear boundary conditions

where u(x,t)and v(x,t)represent thespecies densitiesof thepredator and prey,respectively,Ω is a bounded domain with the smooth boundary∂Ω in Rn,νis the outward unit normal vector on∂Ω and∂ν= ∂/∂ν,d1and d2are the positive diff usion constants,a and b represent the birth rates of u and v,respectively,τrepresents the degree that the predator depends on the prey,and m is the saturation values for the prey.All the above parameters are positive.f(u),g(v)∈ C2(Ω)are nondecreasing and convex functions satisfying f(0)=g(0)=0 and f′(0)=g′(0)>0.

Related problems have been discussed in many papers.Cantrell et al[1,2]considered a kind of logistic model with nonlinear boundary condition,they showed that there is a positive solution bifurcating from the trivial solution.Quoirin and Umezu[3]investigated bifurcation from the zero solution for a logistic elliptic equation with a sign-defi nite nonlinear boundary condition.The related studies to bifurcation of nonlinear boundary problems,we refer to,for instance,[4,5]and references cited therein.Chipot et al[6]studied the behaviour of the time dependent solutions,in particular existence and nonexistence of global solutions and their long time behaviour.Garc´ıa-Meli´an et al[7]provided the precise asymptotic behavior of the solutions to the semilinear elliptic equation.Umezu[8,9]considered the global bifurcation results for semilinear elliptic boundary value problems with indefinite weights,and the existence of bifurcation positive solutions from infinity of a nonlinear elliptic boundary-value problem with nonlinear boundary conditions which arises in population dynamics.Zhang and Wang[10]have studied bifurcation of nonlinear boundary problems in Lotka-Volterra competition model.Compared with the above work which discussed the model for qualitative analysis,author discussed the stability of solution by using the bifurcation.

In this paper,we focus on the stationary problem corresponding to(1),that is

Our purpose is to study the existence and stability of steady states bifurcating from the semi-trivial branch for(1).

2 Preliminaries

For given c(x),b(x)∈C(¯Ω),we defi neλ1(d,c(x),b(x))to be the principal eigenvalue of the following eigenvalue problem

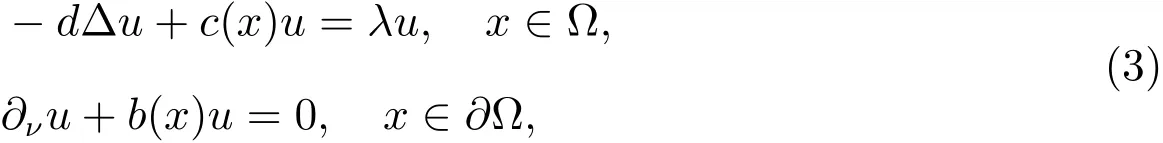
where b(x)≥0.

Lemma 1[11]Suppose that f is an increasing and convex function with f(0)=0.Then(2)has a semi-trivial solution(θ,0),where θis the unique positive solution of

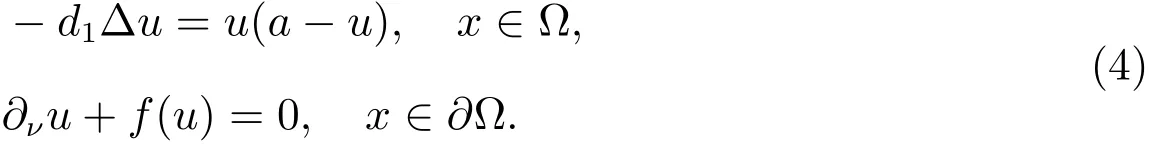
By Lemma 1,there exists a semi-trivial solution branch Γ(θ,0),we denote it by Γ(θ,0)=(b,θ,0).

3 Existence and stability

Let a>d1λ0be fi xed and treat b as a parameter.We denote

For convenience,we denote F(b,u,v):=(F1(b,u,v),F2(b,u,v)).

Clearly,F(b,θ,0)=0.We employ the results in[12]to show that the bifurcation occurs at b= ¯b= λ1(d2,0,g′(0)).The Fr´echet derivative of F(b,u,v)with respect to(u,v)Tat(b,u,v)=(b,θ,0)is given by

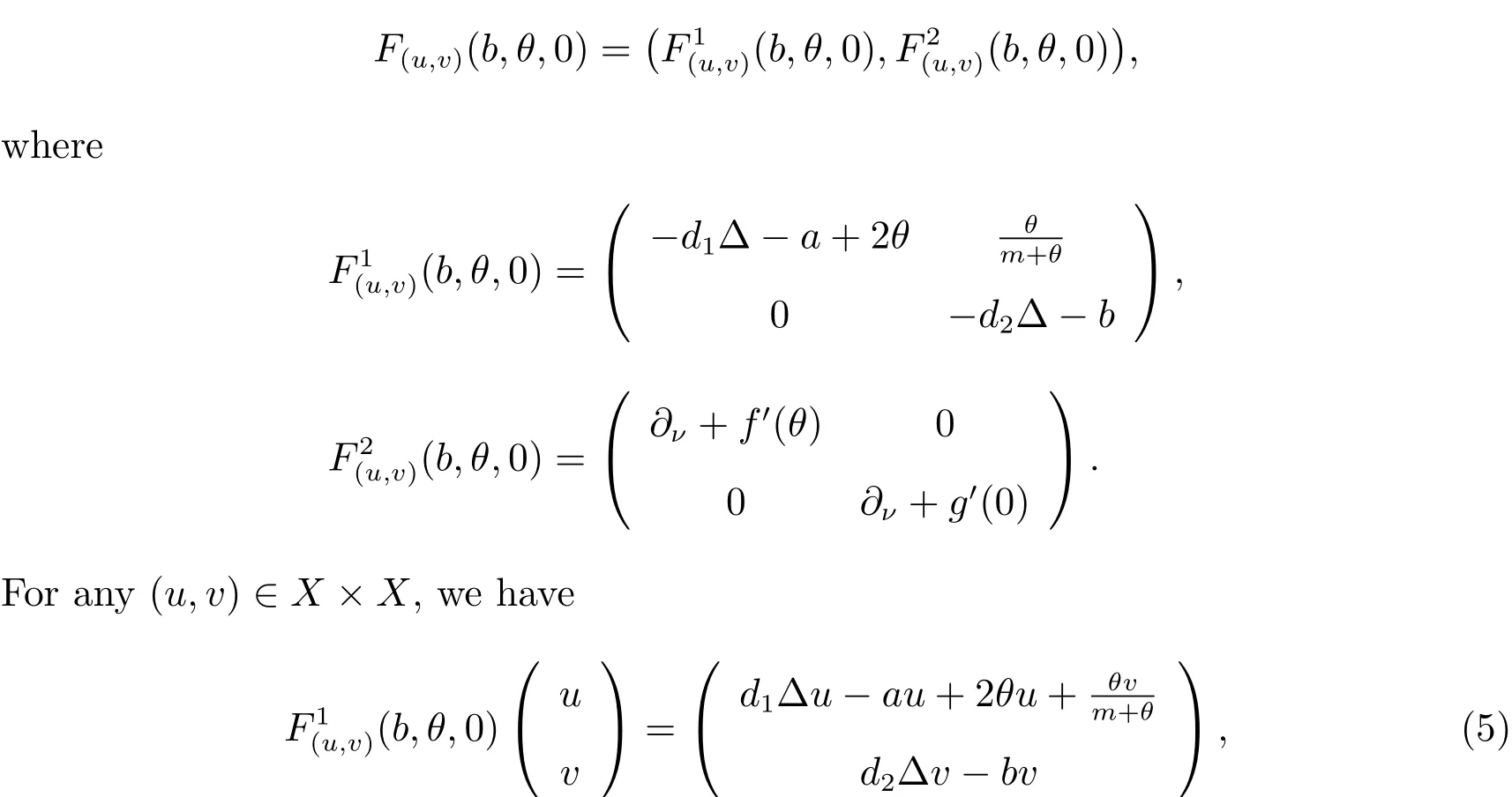
Lemma 2 Consider an eigenvalue problem

Then all eigenvalues of(7)are positive.

Proof Obviously,the principal eigenvalue of(7)isλ1(d1,−a+2θ,f′(θ)).Letφˆ be the eigenfunction corresponding to λ1(d1,−a+2θ,f′(θ)).Then

Multiplying the first equation of(4)byφˆ,and integrating overΩ,we obtain

Similarly,multiplying the first equation of(8)byθ,integrating overΩ,we get

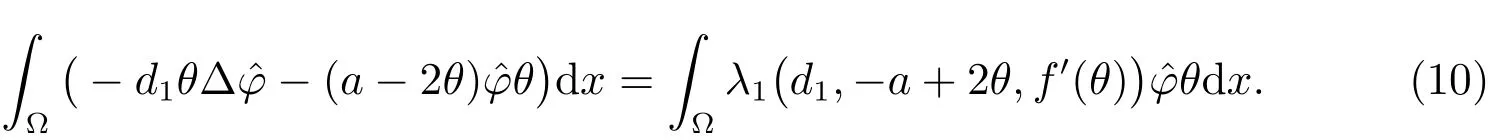
By(9)and(10),it is easy to see that

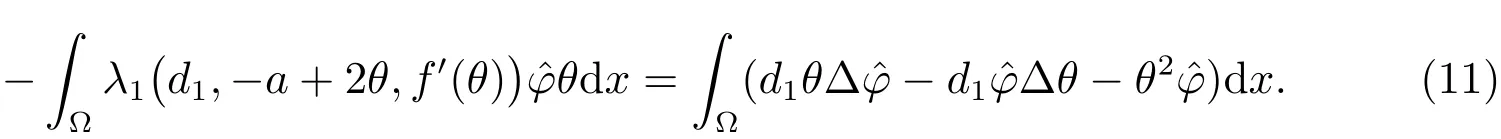
Since f is a convex function in R,we apply the Green’s identity to obtain

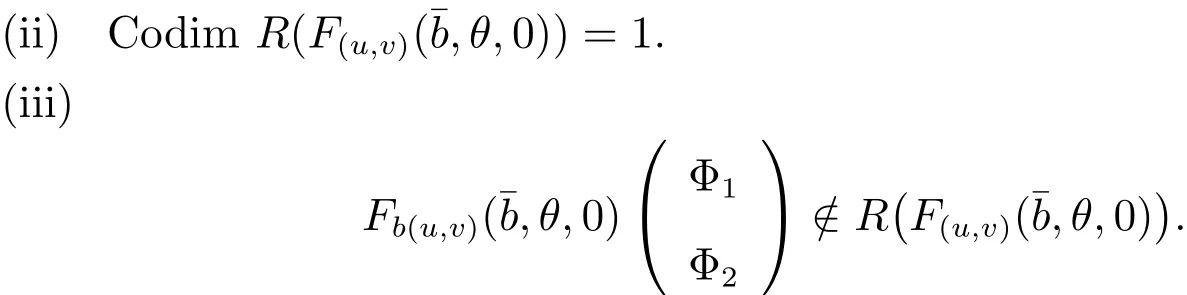
Proof By(5)and(6),the linearization of F(b,u,v)=0 with respect to(u,v)=(θ,0)can be written as

Now,we consider the following problem

By Lemma 2,we know that there exists a unique solution of(14),denoted byΦ1,

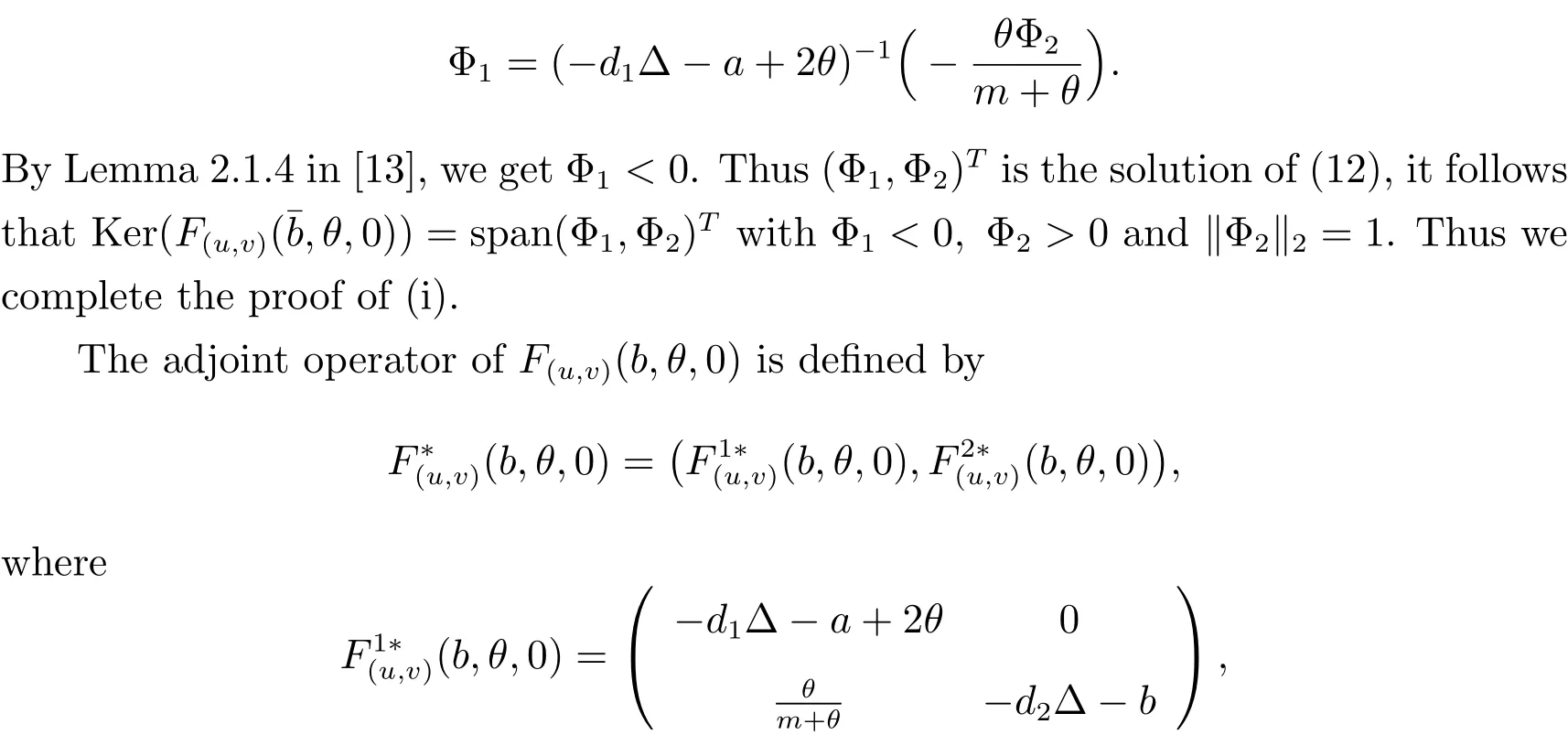
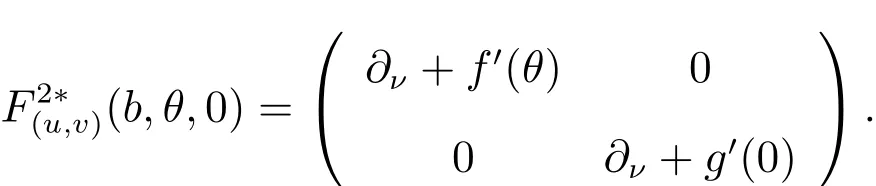
Similarly,we obtain

whereis the principal eigenfunction corresponding to λ1(d1,2θ,(θ)),andis the unique solution of

Thus we have shown(ii).

Finally,we observe that

By(15),(16)and Green’s formula,we have

This is a contradiction.Hence,we conclude that

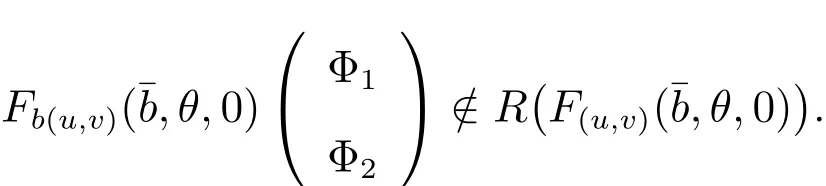
Thus(iii)has been proved.

Theorem 1 There exists a small positive constant s0such that,for any b∈(¯b − s0,+s0),(2)has a solution(,).Moreover:

(i)θ>>0 and>0 inΩ;

(ii) (,)is a nontrivial solution of(2)near(θ,0);

(iii) (,)is asymptotically stable.

Proof By the local bifurcation theory[12]and Lemma 3,we see that(¯b,θ,0)is a bifurcation point from the semi-trivial branch Γ(θ,0).Moreover,there exists a positive number s0and continuously diff erentiable functions(w1,w2)T:(0,s0)→Z,where Z=(Ker(F(u,v)(¯b,θ,0)))⊥and β :(0,s0) → R satisfying following properties:

(d) (b(s),u,v)is a nontrivial solution of F(b,u,v)=0 in a neighborhood of(¯b,θ,0).

This fact implies the existence of a nontrivial solution of(2).SinceΦ1<0,Φ2>0 inΩby Lemma 3,it follows from(17)thatθ>u(s)>0 and v(s)>0 inΩfor suffi ciently small s>0.

Next,we will discuss the stability of(u(s),v(s)).Letγ(s)be the principal eigen-value of F(u,v)(b(s),u,v).According to Theorem 1.16 in[12],

where η(b)is the eigenvalue of F(u,v)(b,θ,0).Obviously, η(¯b)= ¯b − b.Therefore,γ(s)=sβ′(s)(1+o(1))for suffi ciently small s>0.To obtain the asymptotic stability of((s),(s)),We will prove β′(0)>0 for suffi ciently small s>0.

F(b(s),(s),(s))=0 implies that

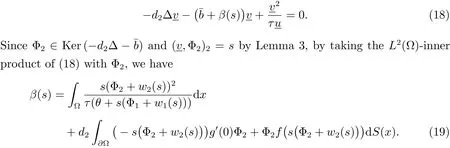
Diff erentiating(19)with respect to s gives

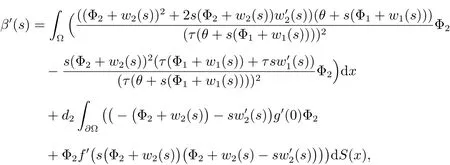
then

By the continuity ofβ′(s),we have γ(s)>0 for suffi ciently small s>0.Thus(iii)has been proved.

4 Numerical simulations

In this section,we present some numerical simulations that verify the analytic results in the previous section by using Matlab.For the system(2),take f(u)=u2,g(v)=v2and transform the spatial domain from Ω =(0,π)to Ω =(0,1).Our numerical simulations illustrate the following major outcome.

In Figure 1,we set d1=0.04,d2=8,a=4,m=3,b=0.5,τ=4.Then(u∗,v∗)=(3,6)is the unique constant solution of(2). Choose(u0,v0)=(u∗+0.7621cos8x,v∗+0.7621cos8x)as the initial value.It is found that the initial perturbation produces some short-time transient spatial structures,after which the system returns to the spatially uniform state(u∗,v∗)=(3,6).The result suggests that the solution of(2)is asymptotically stable.

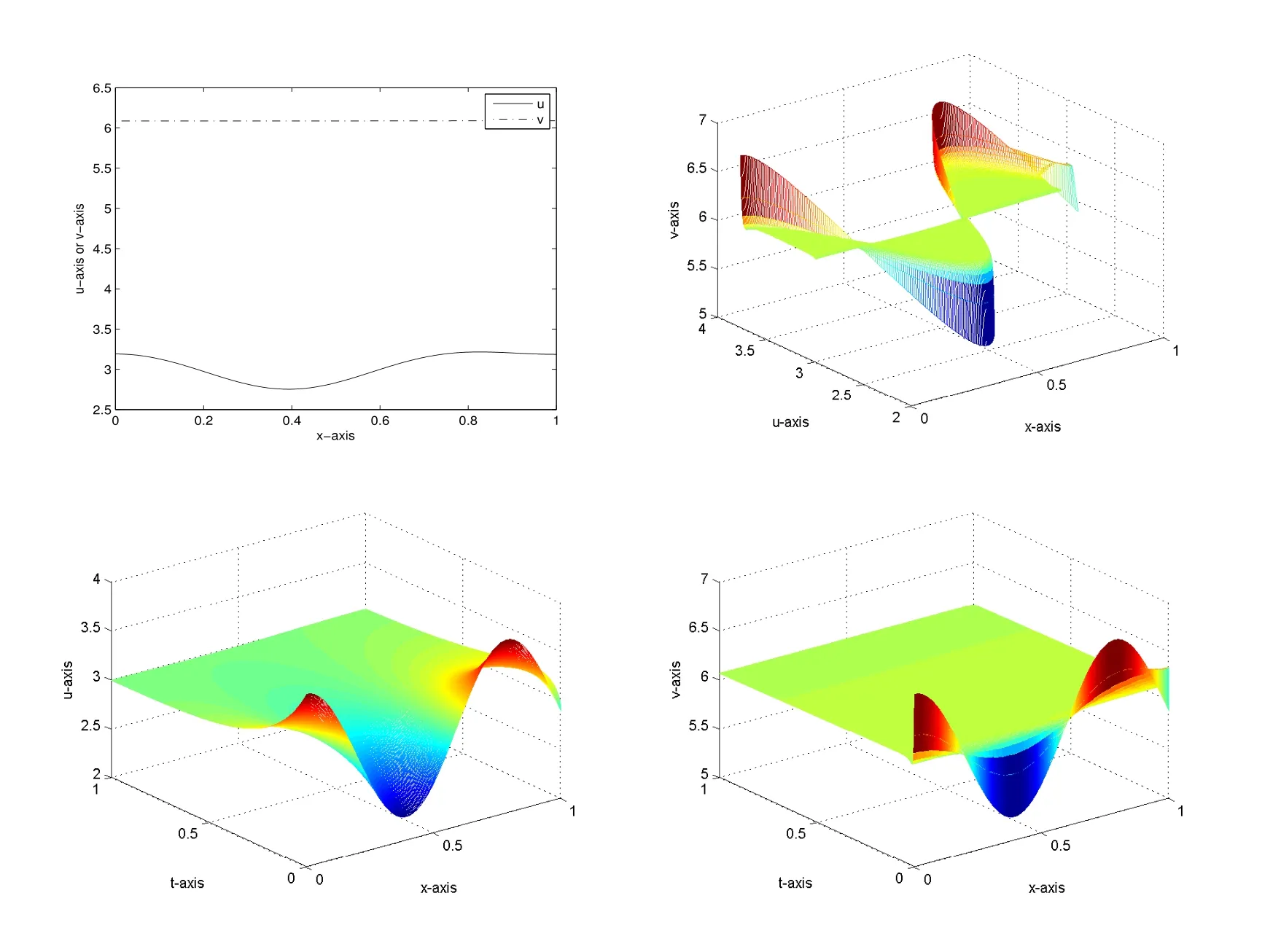
Figure 1:Here d1=0.04,d2=8,a=4,m=3,b=0.5,τ=4

References:

[1]Cantrell R S,Cosner C.On the eff ects of nonlinear boundary conditions in diff usive logistic equations on bounded domains[J].Journal of Diff erential Equations,2006,231(2):768-804

[2]Cantrell R S,Cosner C,Mart´ınez S.Global bifurcation of solutions to diff usive logistic equations on bounded domains subject to nonlinear boundary conditions[J].Proceedings of the Royal Society of Edinburgh,Section A,2009,139(1):45-56

[3]Quoirin H R,Umezu K.Bifurcation for a logistic elliptic equation with nonlinear boundary conditions:a limiting case[J].Journal of Mathematical Analysis and Applications,2015,428(2):1265-1285

[4]Madeira G F,Nascimento A S.Bifurcation of stable equilibria and nonlinear fl ux boundary condition with indefi nite weight[J].Journal of Diff erential Equations,2011,251(11):3228-3247

[5]Shi J P,Wang X F.On global bifurcation for quasilinear elliptic systems on bounded domains[J].Journal of Diff erential Equations,2009,246(7):2788-2812

[6]Chipot M,Fila M,Quittner P.Stationary solutions,blow up and convergence to stationary solutions for semilinear parabolic equations with nonlinear boundary conditions[J].Acta Mathematica Universitatis Comenianae,1991,60(1):35-103

[7]Garc´ıa-Meli´an J,Morales-Rodrigo C,Rossi J D,et al.Nonnegative solutions to an elliptic problem with nonlinear absorption and a nonlinear incoming fl ux on the boundary[J].Annalidi Matematica Puraed Applicata,2008,187(3):459-486

[8]Umezu K.Global bifurcation results for semilinear elliptic boundary value problems with indefi nite weights and nonlinear boundary conditions[J].Nonlinear Diff erential Equations and Applications NoDEA,2010,17(3):323-336

[9]Umezu K.Multiplicity of positive solutions under nonlinear boundary conditions for diff usive logistic equations[J].Proceedings of the Edinburgh Mathematical Society,2004,47(2):495-512

[10]Zhang Y,Wang M X.Bifurcation of Lotka-Volterra competition model with nonlinear boundary conditions[J].Applied Mathematics Letters,2014,38:52-56

[11]Ahn I,Li L G.Positive solutions of certain elliptic systems with density-dependent diff usions[J].Proceedings of the Royal Society of Edinburgh,Section A,1995,125(5):1031-1050

[12]Crandall M G,Rabinowitz P H.Bifurcation,perturbation of simple eigenvalues and linearized stability[J].Archive for Rational Mechanics and Analysis,1973,52(2):161-180

[13]Ye Q X,Li Z Y,Wang M X,et al.Introduction to Reaction-diff usion Equation(2nd Edition)[M].Beijing:Science Press,2011