基于Leonard规正变量的修正高分辨率组合格式∗

牛云霞, 李春光, 景何仿

(1-北方民族大学数学与信息科学学院，银川 750021;2-新疆大学科学技术学院(阿克苏校区)，阿克苏 843000;3-北方民族大学数值计算与工程应用研究所，银川 750021)

doi:10.3969/j.issn.1005-3085.2016.06.002

文章编号:1005-3085(2016)06-0578-09

收稿日期:2015-04-07. 作者简介:牛云霞(1989年10月生)，女，硕士.研究方向：计算流体力学.

∗基金项目:国家自然科学基金(11361002)；宁夏自治区水利厅水资源项目([2015]50-18)；北方民族大学研究生创新项目(YCX1555)；北方民族大学数学与信息科学学院研究生创新项目.

†通讯作者:李春光 E-mail:cglizd@hotmail.com

1 引言

自然界的大部分流动和传热现象都可以用对流扩散方程进行描述．传统的求解对流扩散方程的差分方法，对于大变形及间断问题的计算结果往往无法满足实际需求．因此，高分辨率格式的研究广泛受到学者们的重视．对流扩散方程的扩散项用二阶精度的中心差分格式，可满足大多数工程计算，对流项格式的构造，往往可以决定一个格式的好坏．

本文基于Leonard规正变量，对于不同区域的规正变量进行了重构，得出了求解对流扩散方程的修正高分辨率组合格式，推导出了组合格式计算过程迭代收敛的充分条件．

数值实验表明，新格式满足有界性、稳定性的要求，有效提高了格式的分辨率并减小了解析解与数值解之间的总偏差量．因此，根据计算迭代收敛性的条件在BAIR区域构造的高分辨率组合格式是合理的，具有一定的实际参考价值．

2 规正变量与二阶精度格式

2.1 Leonard规正变量

为了简化高阶组合格式的函数关系定义表达式，根据文献[1]提到的规正变量及规正变量定义图，如图1所示，在一维均匀网格上三个相邻的节点为U,C,D分别表示上游、中间及下游节点，这三个节点上的被求函数值分别记为ϕU,ϕC,ϕD，位于节点之间的界面值记为ϕ(x)．带有迎风倾向的高阶格式可表示为ϕf=f(ϕU,ϕC,ϕD)．

Leonard规正变量定义为

易得=0,=1，因此，引入规正变量后，界面插值函数就仅仅是˜ϕC的函数了，即˜ϕf=f(˜ϕC)，见图2．

图1:常规定义

图2:规正变量定义

2.2 二阶精度格式的推导

一维非稳态对流方程的通用形式为

其中ρ表示流体密度，ϕ表示任意场变量，u表示ϕ在x方向的流动速度．

以图3所示一维均匀网格为例，设速度u>0，变量ϕ在e、w界面的值按照如下形式插值[1]

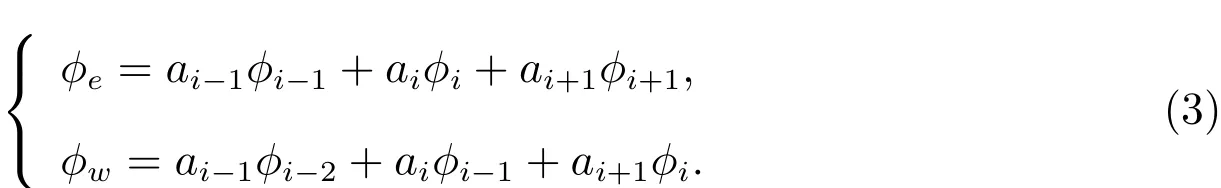
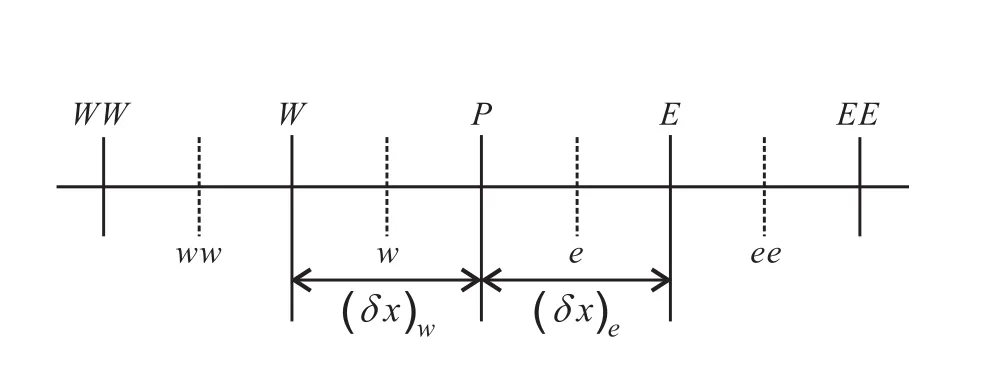
图3:一维均匀网格示意图

为了分析对流项的精度及确定格式定义表达式(3)中的系数ai−1,ai,ai+1的值，我们采用文献[2,3]中Leonard所用的Taylor级数展开法，即

从式(4)可获得求解二阶精度差分格式的限制性条件

求解方程组(5)，并用点ai的值表示点ai−1和点ai+1，可得

因此，满足(7)式的ai取不同的值就形成了不同的二阶差分格式．

根据式(1)，式(7)可整理为

由此得出结论：无论ai取任何值(ai̸=)，二阶精度的差分格式的特征线必然要经过点(0.5,0.75)．Leonard指出特征线通过点(0.5,0.75)的格式都具有至少二阶的精度[1,3]．

利用文献[4,5]的分析方法可得用规正变量定义的二阶精度绝对稳定格式的表达式

为了进一步改进组合格式，1988年，Gaskell与Lau[6]提出了一种对流项差分格式有界性准则(GL-CBC,convective boundedness criterion)，文献[7]认为GL-CBC仅仅是一个充分条件，并提出了拓宽的对流有界性准则(ECBC,extended convective boundedness criterion)．通过仔细研究GL-CBC和ECBC，计算发现某些满足上述两个准则的格式计算精度低，根据文献[1]提到的新通用对流有界性准则(GCBC,generalized convective boundedness criterion)，GL-CBC和ECBC是这一判据的两种极限情况．

文献[1]指出，在NVD中构建有界且精确的合理插值方法应该满足以下条件：

(a)GL-CBC准则；

(b) 在NVD区域特征线应该通过(0.5,0.75)；

(c) 下式变量参数的最大绝对值须在[−0.125,0.375]范围内，以满足插值的合理性：

上述三个条件被称为BAIR(boundedness accuracy and interpolative reasonableness)．在图4中虚线区域加上区域外两段一阶迎风线(˜ϕC<0和˜ϕC>1)表示BAIR区域．在此区域内格式有界，至少具有二阶精度且具有插值合理性．在NVD上，BAIR包括三个必经点O(0,0),Q(0.5,0.75),P(1,1)这也是所有高阶组合格式应通过的点．

图4:BAIR区域

3 高分辨率组合格式的构造

依据规正变量定义得出的高分辨率组合格式可以写成以下的通用形式

其中mC与kC在的某一取值范围内均为常数．

根据式(1)，式(9)可写为

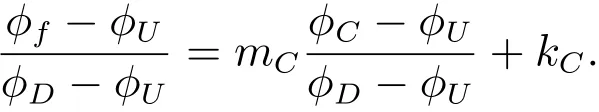
由此可以得出

则方程(12)的迭代矩阵为严格对角占优矩阵，此时TDMA算法迭代过程是收敛的[10-12]．

综上可得结论，在NVD中构建有界且计算过程迭代收敛的差分格式应该满足以下条件：

(a) 高分辨率格式是在BAIR区域构造的；

(b) 格式的参数满足ki<3mi+−1．

基于以上理论分析，本文提出了修正高分辨率组合格式(即Mnew格式)．由于特征线靠近一阶迎风时，格式具有较高的扩散，因此可以选择远离一阶迎风的特征线减小扩散．下面列出新格式与已有格式的表达式：

Mnew格式：

根据式(10),(14)和(15)可得β<+．在新格式中参数β不再是一个经验参数，定义为β=0.45+．因此，参数β可根据网格比r的分布自适应的得到．数值算例表明，新格式总偏差量较小且具有高分辨率的特性．

根据式(10)和式(15)可得Mnew格式一般表达式

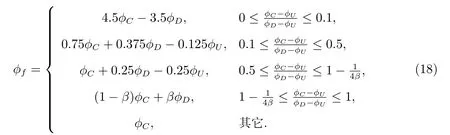
4 数值算例

为了比较不同格式的精度，定义下列偏差量

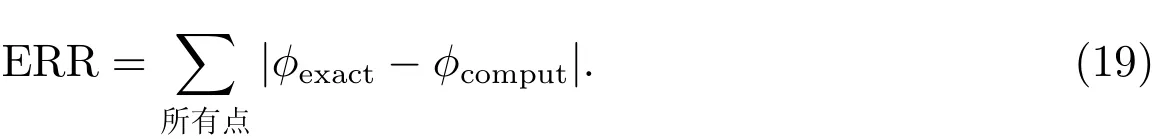
算例中对流项离散分别为FUD格式、QUICK格式、MINMOD格式、HOAB格式和Mnew格式，模拟时间t=1空间网格步长和时间步长分别取为h=0.065,τ=0.01．

算例1 考虑初值问题

其中

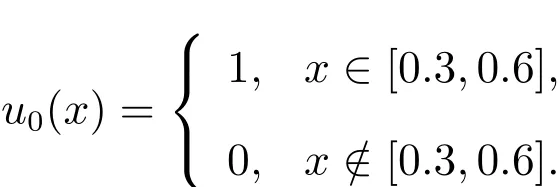
计算结果如图5所示，偏差量如表1所示．

表1:对流问题不同格式偏差量的分布

算例2 考虑对流扩散问题

计算结果如图6所示，偏差量如表2所示．

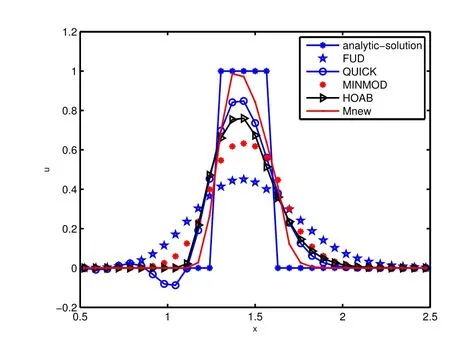
图5:对流问题数值模拟结果的比较

图6:对流扩散问题数值模拟结果的比较

表2:对流扩散问题不同格式偏差量的分布

对于纯对流问题从图5的计算结果可以看出：QUICK格式发生了越界现象；FUD格式的数值耗散现象比较严重，格式分辨率较低．对于对流扩散问题从图6的计算结果可以看出：FUD格式发生了越界现象；QUICK格式分辨率较低．Mnew格式的数值耗散低于HOAB格式，HOAB格式低于MINMOD格式．总之，Mnew格式具有高分辨率的特性，能够敏锐捕捉到大梯度变化的流动现象，数值结果稳定性好．

从表1与表2的计算结果可得出结论：与经典格式相比Mew格式的总偏差量最小，在相同条件下新格式逼近解析解的效果优于其他格式．

因此，在BAIR区域基于收敛性理论构造的新格式具有一定的实际参考价值．

5 结论

本文在已有高分辨率组合格式的基础上，根据Leonard规正变量定义，构造了对流项离散格式的修正高分辨率组合格式．通过算例比较分析了FUD格式、QUICK格式、MINMOD格式、HOAB格式和Mnew格式，数值模拟结果表明与经典格式相比Mnew格式具有高分辨率的特性，总偏差量较小，能很好的模拟场变量的大梯度变化，计算结果优于传统格式．

参考文献：

[1]陶文铨.传热与流动问题的多尺度数值模拟方法与应用[M].北京：科学出版社，2008 Tao W Q.Multiscale Numerical Simulation Methods and Applications of Heat Transfer and Flow Problems[M].Beijing:Science Press,2008

[2]Leonard B P.Simple high-accuracy resolution program for convective modeling of the discontinuities[J].International Journal for Numerical Methods in Fluids,1988,8(10):1291-1318

[3]Leonard B P.The ULTIMATE conservative diff erence scheme applied to unsteady one-dimensional advection[J].Computer Methods in Applied Mechanics and Engineering,1991,88(1):17-74

[4]陶文铨.数值传热学(第2版)[M].西安：西安交通大学出版社，2001 Tao W Q.Numerical Heat Transfer(2nd Edition)[M].Xi’an:Xi’an Jiaotong University Press,2001

[5]Tao W Q,Sparrow E M.The transportive property and convective numerical stability of the steady state convection-diff usion fi nite diff erence equation[J].Numerical Heat Transfer,1987,11(4):491-497

[6]Gakell P H,Lau A K C.Curvature compensated convection transport:SMART,a new boundednesspreserving transport[J].International Journal for Numerical Methods in Fluids,1988,8(6):617-641

[7]Yu B,Tao W Q,Zhang D S,et al.Discussion on numerical stability and boundedness of convective discretized scheme[J].Numerical Heat Transfer,Part B:Fundamentals,2001,40(4):343-365

[8]李人宪.有限体积法基础[M].北京：国防工业出版社，2005 Li R X.Foundation of Finite Volume Method[M].Beijing:National Defense Industry Press,2005

[9]陆金甫，关治.偏微分方程数值解法(第2版)[M].北京：清华大学出版社，2005 Lu J F,Guan Z.The Numerical Method for Solving Partial Diff erential Equations(2nd Edition)[M].Beijing:Tsinghua University Press,2005

[10]陈世军，张凯院.一类矩阵方程组的对称解及其最佳逼近[J].工程数学学报，2009,26(4):711-715 Chen S J,Zhang K Y.Symmetric solution of a class of matrix equations and its optimal approximation solution[J].Chinese Journal of Engineering Mathematics,2009,26(4):711-715

[11]徐树方，高立，张平文.数值线性代数[M].北京：北京大学出版社，2000 Xu S F,Gao L,Zhang P W.Numerical Linear Algebra[M].Beijing:Beijing University Press,2000

[12]关朋燕，李春光，景何仿.TDMA算法在迭代求解二维对流扩散问题中的收敛性证明[J].高等学校计算数学学报，2014,36(1):77-85 Guan P Y,Li C G,Jing H F.Proof on the convergence of TDMA algorithm in the iterative solution of twodimensional convection-diff usion problems[J].Numerical Mathematics:A Journal of Chinese Universities,2014,36(1):77-85

Received:07 Apr 2015. A ccep ted:01 Dec 2015.

Found ation item:The National Natural Science Foundation of China(11361002);the Ningxia Water Resources Project([2015]50-18);the Graduate Student Innovation Projects of Beifang University of Nationalities(YCX1555);the Graduate Student Innovation Projects of School of Mathematics and Information Science of Beifang University of Nationalities.

†Cor r esp ond ing author:C.Li.E-mail address:cglizd@hotmail.com