考虑风速随机特征的多工况电力系统稳定性分析

马 静 ，高 翔 ，李益楠 ，王增平

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.国网冀北电力有限公司廊坊供电公司，河北 廊坊 065000）

0 引言

风电的发展是世界各国未来能源战略的重要组成部分，但风机出力的波动性往往导致系统运行工况发生大范围变化，这为电力系统的安全稳定与经济运行带来了巨大风险［1-4］。因此，迫切需要对含风速随机特征的多工况电力系统稳定性进行深入研究。

目前，有关风电接入下电力系统的稳定性研究主要集中在风机自身以及电网侧单一运行工况下的稳定性方面。文献［5-7］研究了不同风机接入下风功率变化对风机自身稳定性的影响，然而该方法并未对风机接入后网侧电力系统的稳定性进行分析；文献［8-10］分析了风电接入下风功率变化对网侧电力系统振荡模式的影响，并指出在采用定子电压锁相环的情况下可以使用静态功率源代替高阶风机模型分析电力系统机电振荡，但是该方法仅针对电力系统的单一运行工况进行分析，并未给出多工况下电力系统稳定性分析方法。文献［11-12］针对风机的功率变化特性，将时域仿真法与蒙特卡罗法相结合分析多工况下电力系统的稳定性，然而为保证计算结果的精确性，蒙特卡罗法需要生成大量计算场景，因此对于大规模电力系统的稳定性分析研究将非常耗时。

针对上述问题，本文提出一种考虑风速随机特征的多工况电力系统稳定性分析方法。首先利用参数Weibull模型拟合预测短时间内的风速变化趋势，并将风速区间化，同时，选取条件特征风速，计算条件特征风速概率密度矩阵；然后根据风速与风机出力分段函数确定系统运行工况，建立连续蒙特卡罗多工况电力系统模型；在此基础上，构建Lyapunov泛函，利用Dynkin引理对泛函的弱无穷小算子进行变换，推导出满足干扰衰减度γ的鲁棒随机稳定线性矩阵不等式（LMI），并转化为可行性问题，以判断系统是否稳定。IEEE 4机11节点系统和16机68节点系统时域仿真结果均表明该方法能够快速有效地对多工况下的电力系统稳定性进行分析，计算量小，简单可行。

1 考虑风速随机特征的多工况电力系统模型

风机出力受风速随机特征影响呈现多种运行方式，若恰当地对风速的随机特征进行分析，模拟含风机出力影响的电力系统运行状态，则能对考虑风速随机特征的多工况电力系统稳定性进行有效分析。

1.1 条件风速概率密度与风机出力模型

定义条件风速概率密度［13-14］为某一条件特征风速下，下一时刻（采样间隔10min）或若干时刻后的风速概率密度。采用双参数Weibull分布拟合风速条件概率密度曲线。

双参数Weibull分布可描述为：

其中，vi为当前时刻风速；k为形状系数；c为尺度系数。

风速的概率分布函数为：

忽略电气损耗以及风电场尾流等因素，风电机组出力与风速之间的近似函数关系可以表示为：

其中，vci为风电机组切入风速；vco为风电机组切出风速；vR为风电机组额定风速；PR为风电机组额定输出功率。

由式（1）—（3）得到风电机组输出功率的分段概率函数为：

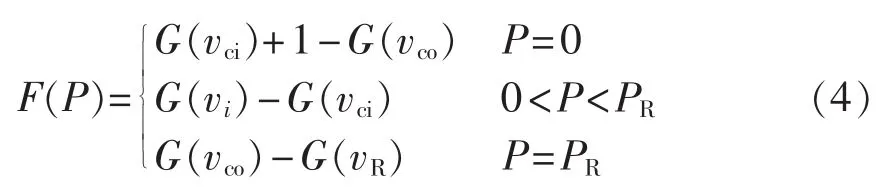
1.2 基于连续蒙特卡罗的多工况电力系统模型

系统的多工况模型可用连续蒙特卡罗跳变系统表示为：

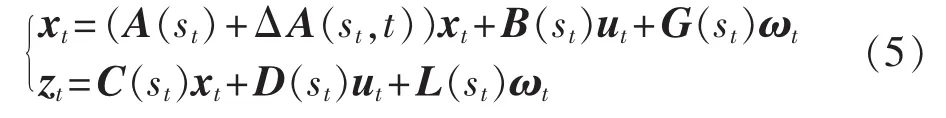
其中，xt∈Rn为状态向量；ut∈Rp为控制输入向量；zt∈Rr为控制输出向量；ωt为白噪声，满足E｛dωt｝=0，为在有限空间 S=｛1，2，…，l｝中取值的连续蒙特卡罗过程，对应各个风速模式下的系统运行工况，描述系统工况随风机出力变化的演化过程，其状态转移概率密度可以表示为式（6）。

其中，H为转移概率；st为处于t时刻的系统状态；st+Δ为处于t+Δ时刻的系统状态；矩阵π表示蒙特卡罗转移概率密度矩阵，πij为系统运行工况在t时刻处于i而在t+Δ时刻处于j的转换概率密度。

其中，状态概率密度πij可由状态概率Pij和式（1）—（4）计算求得。

对于每一个 st=i∈S，记 A（st）、B（st）、G（st）、C（st）、D（st）、L（st）分别表示为 Ai、Bi、Gi、Ci、Di、Li，并且不确定参数满足匹配性条件：

其中，Hi和Mi为已知矩阵；实矩阵 F（i，t）反映了系统不确定参数的结构信息，满足式（9）。

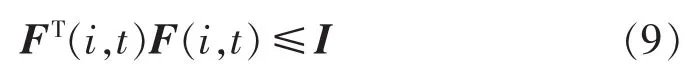
2 考虑风速随机特征的多工况电力系统稳定性分析方法

定义 1［15］对于式（5）所示系统，当 ut=0 以及所有的初始条件x0∈Rn和s0∈S成立时，若满足：

则形如式（5）的连续蒙特卡罗系统随机稳定。

定理1给定正常数γ＞0，若存在一组正定对称矩阵 Pi＞0（i∈S），使得如下一组矩阵不等式成立：

则当ut=0时，式（5）所示系统鲁棒随机稳定，且满足扰动衰减度γ，即：

其中，Ai、Ci、Gi、Li为式（5）所示系统各部分系数矩阵；“*”为矩阵中对称部分的简写；P（s0）为适维正定对称矩阵。

证明如下。

利用Schur定理，由式（11）可知：

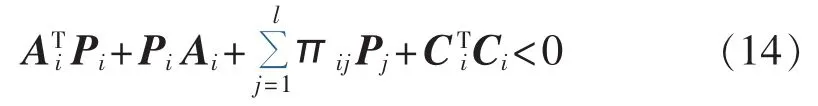
由于对 i∈S，有，故：

因此，只需证明式（15）成立的条件下，式（5）所示系统鲁棒随机稳定，即可证明定理1的鲁棒随机稳定判据成立。

构造Lyapunov泛函：

当 ωt=0 时，由泛函 V（xt，i）的弱无穷小算子可知：

其中，l为弱无穷小算子符号。

即存在一组正定矩阵 Qi＞0（i∈S），使得：

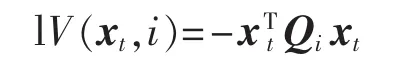
从而：

其中，λmin［Qi］为矩阵 Qi特征根的最小值。

由Dynkin引理，有：

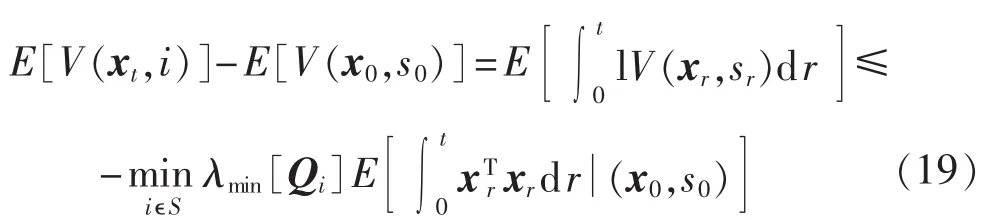
由式（19）可知：

因此，有：

当t ∞时，有：

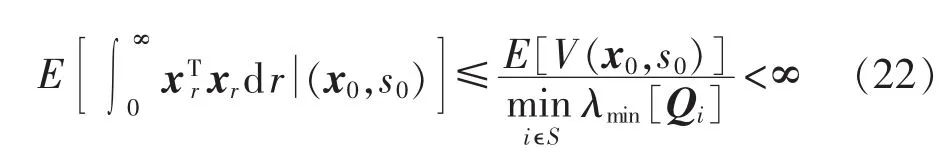
由式（15）—（22）可知式（5）所示系统随机稳定。

当 ωt≠0 时，泛函 V（xt，i）的弱无穷小算子可表示为：

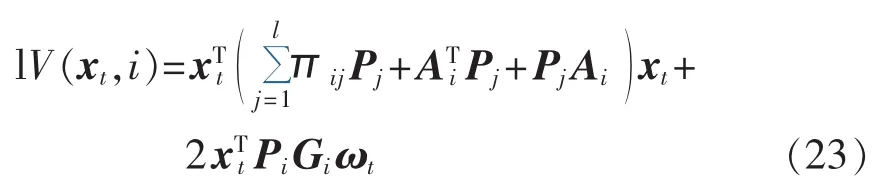
定义指标函数：

由于：

因此：

由Dynkin引理，有：

由 E［V（xT，sT）］≥0 以及式（15），有：

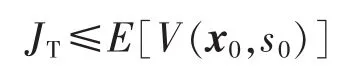
当T ∞时，有：

即由式（23）—（26）知，式（11）使得式（5）所示系统具有扰动衰减度γ。

定理1中判据是个LMI的可行性问题，可以通过MATLAB LMI工具包中的feasp求解器进行求解。 即对于给定的 LMI系统 A（x）＜B（x），通过求解式（27）所示辅助凸优化问题，寻找到全局最小标量值 ξmin，如果 ξmin＜0，则存在 x∈Rn满足下式：

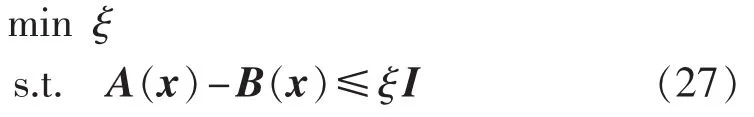
故式（5）所示多工况电力系统模型的稳定性可采用如下优化问题表示：

利用LMI工具包对式（28）进行求解，若存在ξ＜0以及满足定理1所示正定矩阵Pi＞0，则式（5）所示系统鲁棒随机稳定，且满足扰动衰减度γ；否则，系统不稳定。

3 算例分析

3.1 条件风速概率密度矩阵的求取

以某风电场1个月内实测风速数据为例进行分析，其中切入风速为 3 m／s，额定风速为 12 m／s，切出风速为22 m／s，风机输出功率曲线如图1所示。以1 m／s为区间宽度将风速划分为10个模式，构成连续蒙特卡罗模型状态集合，记作 S=｛1，2，…，10｝，各模式信息在表1中给出。

图1 风电机组功率曲线Fig.1 Power curve of wind turbine

概率密度转移矩阵的详细求解过程如下。

加入左联后的鲁迅以其丰硕的创作实绩和其巨大的影响力和感召力进行着工作。他阅读并翻译了多种苏联文艺作品和理论著作，用犀利的文笔与当时国民党政府的文化围剿进行斗争，“左联”五位青年进步作家，被国民党逮捕杀害，鲁迅随即写下《黑暗中国的文艺现状》等文章，揭露国民党政府的罪行。鲁迅积极地进行被害同志的营救工作，在瞿秋白、陈赓、廖承志、丁玲等人的营救工作中，奔走呼号，做了极大的努力。1935年冬，中共北方局跟党中央失去了联系，他又为党接通了这条中断的线，使革命工作得以顺利进行。

（1）在某一条件风速的前提下，根据风速采样数据寻找与条件风速相等的所有数据点，取这些点下一时刻或若干个时刻的风速数据构成新的数据子集，得到表1中各个条件风速下的转移概率矩阵。

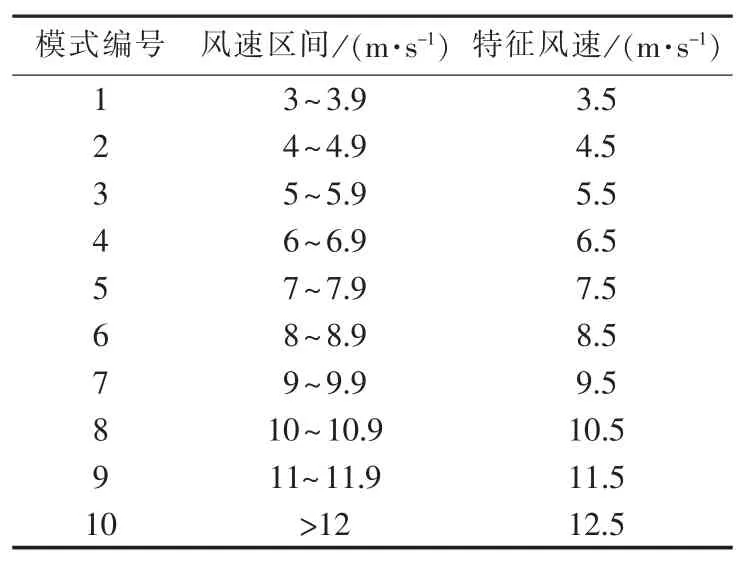
表1 条件风速模式Table 1 Modes of conditional wind speed

（2）将转移概率矩阵的每一行代入式（2）进行拟合，可得到该条件风速下的Weibull拟合系数，结果如表2所示。

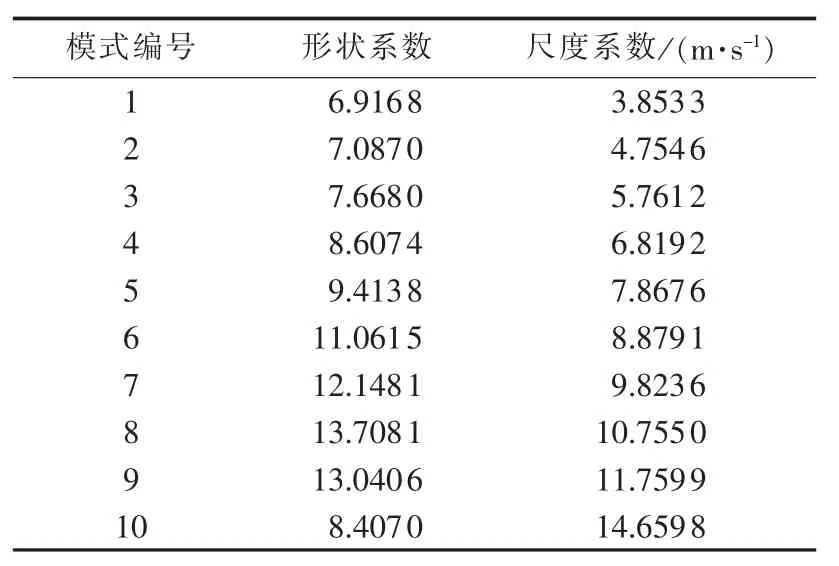
表2 风速模式下条件风速概率密度的Weibull拟合系数Table 2 Weibull fitting coefficients of conditional wind speed probability density for different wind speed modes

（3）根据表2及式（1）求得各条件风速概率密度矩阵如式（29）所示。

3.2 4机系统

以IEEE 4机11节点系统为例，系统结构图如图2所示，该系统包含区域1与区域2这2个区域，其中发电机G1和G2位于区域1，发电机G3和G4位于区域2，2个区域之间的联络线7-8与8-9均为双回线。发电机采用6阶详细模型，励磁系统采用快速励磁，基准模型下的负荷采用50%恒阻抗和50%恒电流模型。仿真时将区域2中发电机G4以等容量的功率源代替，以模拟风机输出功率的工况变化情况［10］。

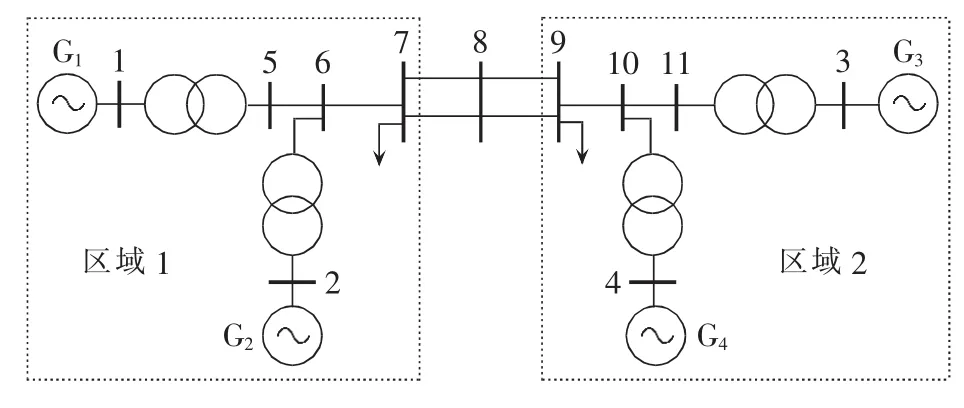
图2 4机2区域电网结构图Fig.2 4-machine 2-area power system

首先，利用模态分析法得到4机系统相应风机出力模式下的状态矩阵并利用选择模式分析SMA（Selective Model Analysis）方法将系统降到8阶，降阶后的状态矩阵只保留与发电机机电暂态相关的状态量，即发电机功角和发电机转速［16］。然后，将降阶后的系统状态矩阵与式（29）所示状态转移概率密度矩阵代入式（28），扰动衰减度γ取0.1，利用可行性问题求解方法求得该LMI成立，且存在正定矩阵Pi，4机系统鲁棒随机稳定。 其中，式（30）、（31）给出了部分正定矩阵Pi的取值。

由上述计算结果可知，该4机系统满足定理1所示鲁棒随机稳定条件，即该系统在考虑风速随机特征时为鲁棒随机稳定的系统。

图3和图4分别就系统实际运行中可能出现的运行工况变化情况进行时域仿真，其中，图3为系统仅发生一次工况变化情况下，发电机G2与G3间的相对功角δ23的动态响应，图4为系统发生多工况变化情况时发电机G2与G3间的相对功角的动态响应。图中系统实际仿真结果与本方法判断结果一致。由此验证了本方法的有效性和正确性，同时，该方法可在不获取运行轨迹的前提下准确判别系统稳定性，计算量少。

图3 4机系统单工况变化情况下发电机G2-G3相对功角动态响应Fig.3 Dynamic response of relative power angle between G2and G3to single operating condition change of 4-machine system

图4 4机系统多工况变化情况下发电机G2-G3相对功角动态响应Fig.4 Dynamic response of relative power angle between G2and G3to multiple operating condition changes of 4-machine system

3.3 16机系统

以IEEE 16机68节点的新英格兰—纽约互联系统为例，系统结构如图5所示。该系统可分为五大区域，其中区域1、2和3为等值系统，区域4为纽约系统，区域5为新英格兰系统，将区域3中发电机G16以等容量的功率源代替，以模拟风机输出功率的变化情况。发电机采用6阶详细模型，励磁采用IEEE-DC1型励磁，负荷模型采用WECC负荷模型，80%的恒有功负荷，80%的恒无功阻抗负荷，20%的动态负荷。

图5 16机68节点电网结构图Fig.5 16-machine 68-bus power system

首先利用SMA方法分别将各工况下系统状态矩阵降到32阶，并将降阶后的系统状态矩阵与式（29）所示概率密度转移矩阵代入式（28），扰动衰减度γ取0.1，利用可行性问题求解方法求得该LMI成立。由于所得矩阵Pi中P6存在负数特征根 -15.3827，即矩阵Pi存在非正定矩阵，因此，该16机68节点系统的新英格兰—纽约互联系统在考虑风机出力变化时不满足鲁棒随机稳定条件。

图6和图7分别就系统实际运行中可能出现的运行工况变化情况进行时域仿真，其中，图6为系统仅发生一次工况变化情况时发电机G1与G8间的相对功角δ18动态响应，图7为多次工况变化情况下发电机G1与G8间的相对功角δ18动态响应。由图可知，系统在单次与多次工况变化情况时均存在不稳定情况，这与本方法的判稳结果一致。

分别对系统各运行工况的状态矩阵做进一步分析，各状态矩阵最小阻尼比如表3所示。由表3可知，各运行模式下状态矩阵特征值均具有负实部，此时，若利用特征值分析法单独分析任一运行工况的稳定性，分析结果均为稳定。然而，在考虑风速随机特征的多工况电力系统中，系统从一个稳定工况切换到另一个稳定工况时可能发生失稳，因此，该现象是传统针对单一工况的稳定性分析方法无法分析的现象，但本方法却能够有效针对这一现象进行稳定性判别。

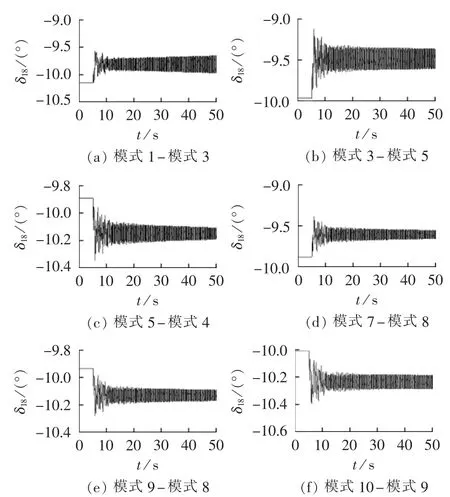
图6 16机系统单工况变化情况下发电机G1-G8相对功角动态响应Fig.6 Dynamic response of relative power angle between G1and G8to single operating condition change of 16-machine system

图7 16机系统多工况变化情况下发电机G1-G8相对功角动态响应Fig.7 Dynamic response of relative power angle between G1and G8to multiple operating condition changes of 16-machine system

表3 16机系统各运行模式最小阻尼比Table 3 Minimum damping ratio of 16-machine system for different operating modes

4 结论

本文提出了一种考虑风速随机特征的多工况电力系统稳定性分析方法。该方法具有以下特点：

（1）将电力系统按照风速随机特征划分成不同的运行工况，以此建立连续蒙特卡罗多工况电力系统模型，分析多工况电力系统稳定性；

（2）将电力系统的多工况稳定性问题转化为可行性求解问题，无需获取系统实际运行轨迹，计算量小，应用便捷；

（3）风机出力变化导致系统运行工况发生变化，为系统的稳定性带来了新的问题，基于连续蒙特卡罗的多工况电力系统稳定判据能有效解决这一问题。

［1］YAO Wei，JIANG Lin，WEN Jinyu，etal.Wide-areadamping controller of FACTS devices for inter-area oscillations considering communication timedelays［J］.IEEE Transactionson Power Systems，2014，29（1）：318-329.

［2］STEWART G P，BRENDAN P M，DONALD G H.Regions of active damping control for LCL filters［J］.IEEE Transactions on Industry Applications，2014，50（1）：424-432.

［3］BERNABEU E E，THORP J，CENTENO V.Methodology for a security／dependability adaptive protection scheme based on data mining ［J］.IEEE Transactions on Power Delivery，2012，27（1）：104-111.

［4］MA J，WANG T，WANG Z.Intervaleigenvalue analysisof closed-loop control for power system oscillation with interval parameters［C］∥Power and Energy Society General Meeting，2012 IEEE.San Diego，California，USA：IEEE，2012：1-6.

［5］SLOOTWEG J G，KLING W L.The impact of large scale wind power generation on power system oscillations［J］.Electric Power Systems Research，2003，67（1）：9-20.

［6］HU Jiabing，HUANG Yunhui，WANG Dong，et al.Modeling of grid-connected DFIG-based wind turbines for DC-link voltage stability analysis［J］.IEEE Transactions on Sustainable Energy，2015，6（4）：1325-1336.

［7］MEI F，PAL B.Modal analysis of grid-connected doubly fed induction generators［J］.IEEE Transactions on Energy Conversion，2007，22（3）：728-736.

［8］GASCA J J S，MILLER N W，PRICE W W.A modal analysis of a two-area system with significant wind power penetration［C］∥Proc 2004 IEEE PES Power Systems Conf Expo.New York，USA：［s.n.］，2004：1148-1152.

［9］VITTALE，O’MALLEY M，KEANE A.Rotor angle stability with high penetrations of wind generation［J］.IEEE Transactions on Power Systems，2012，27（1）：353-362.

［10］王志文，沈沉，刘锋.不同锁相机制的双馈电机对电力系统小干扰稳定的影响分析［J］. 中国电机工程学报，2014，34（34）：6167-6176.WANG Zhiwen，SHEN Chen，LIU Feng.Analysis on impact of doubly fed induction gener ationswith differentphaselock mechanism on power system small signal stability［J］.Proceedings of the CSEE，2014，34（34）：6167-6176.

［11］XU Z，DONG Z Y，ZHANG P.Probabilistic smallsignal analysisusing Monte Carlo simulation［C］∥Proceedingsof IEEE Power Engineering Society General Meeting.Piscataway，NJ，USA：IEEE，2005：1658-1664.

［12］WANG C，SHI L B，YAO L Z，et al.Modelling analysis in power system small signal stability considering uncertainty of wind generation［C］∥IEEE Power and Energy Society General Meeting.Minneapolis，USA：IEEE Power and Energy Society，2010：1-7.

［13］RIAHY G H，ABEDI M.Short term wind speed forecasting for wind turbine applications using linear prediction method ［J］.Renewable Energy，2008（33）：35-41.

［14］彭虎，郭钰锋，王松岩，等.风电场风速分布特性的模式分析［J］.电网技术，2010，34（9）：206-210.PENG Hu，GUO Yufeng，WANG Songyan，et al.Pattern analysis on characteristics of wind speed distribution in wind farms［J］.Power System Technology，2010，34（9）：206-210.

［15］FENG X B，LOPARO K A，JI Y D，et al.Stochastic stability properties of jump linear systems［J］.IEEE Transactions on Automatic Control，1992，37（l）：38-53.

［16］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京：清华大学出版社，2002：269-270.