基于运行数据和高斯过程回归的风电机组发电性能分析与监测
2016-05-22姜漫利李航涛
郭 鹏,姜漫利,李航涛
(华北电力大学 控制与计算机工程学院,北京 102206)
0 引言
近年来,我国风电产业正在由粗放式发展向精细化发展转变,风力发电企业对已投运的风电机组的运行管理越来越重视。每台机组发电性能的高低对风电场的运行经济效益有着重要的影响。风电机组的发电性能通常用风能利用系数表示,反映其对风能的利用效率,是机组性能好坏的重要标志,较高的发电性能或风能利用系数能够提高风电机组的年发电量。由于风电机组运行环境恶劣,运行工况复杂多变,导致机组的实际发电性能往往偏离机组的设计指标,风能利用系数降低。文献[1]研究了叶片安装误差对风电机组性能的影响;文献[2]首先建立双馈风电机组模型,在此基础上从风能最大利用和安全运行角度,提出考虑发电机损耗最小的功率控制策略来提高机组发电性能;文献[3]讨论了风剪切效应对发电量的影响;空气密度对风电机组发电性能也有一定影响,文献[4]分析了不同海拔高度下空气密度对机组发电量的影响,通过优化叶片翼型提高发电性能;文献[5]以功率曲线为风电机组性能的评价标准,比较了最大值法、最大概率法和比恩法3种功率曲线建模方法,并估计了不确定度;文献[6]采用模糊滑模控制来改进风电机组控制系统性能。风电机组监控与数据采集(SCADA)系统记录了机组的环境因素(风速、气温等)和各个重要组成部件的运行参数,全面反映了机组的运行状态和性能。本文以风电机组的SCADA运行数据为基础,首先对影响风电机组发电性能的因素进行了详细分析,进而采用高斯过程回归方法建立风电机组的发电性能模型。该模型能够实时监测风电机组发电性能的变化,当发电性能异常降低时,及时提醒运行人员检查风电机组各个部件的运行状态。
1 风电机组发电性能影响因素分析
待研究的风电机组为张家口某风电场额定功率为1.5 MW的变桨变速双馈机组。该机组切入风速、额定风速、切出风速分别为3m/s、12m/s和25 m/s,叶轮直径为77 m。该机组的SCADA系统采用10 s和10 min 2种不同时间间隔记录环境参数和各个重要部件传感器的测量参数。10 s和10 min间隔记录的内容相同,每条记录包括时间标签、风速、功率、环境温度、叶轮转速、叶片桨距角、偏航误差等共计46个参数。如前所述,风电机组的发电性能利用风能利用系数描述,风能利用系数为:

其中,P为某时刻机组实发功率;ρ为空气密度;A为叶轮扫风面积;v为该时刻风速。由动量理论,风能利用系数最大不超过贝兹极限,即0.593。风能利用系数越大,风电机组从风资源中获取的能量越多,发电性能越高。
变桨变速风电机组通常具有几个不同的运行区域。在切入风速和额定风速之间,机组工作在最大风能追踪阶段。在此区间,机组的桨距角固定(一般在0°~2°附近),机组的转速和转矩随风速变化,使叶尖速比接近最佳值,达到最大风能追踪的目的。在额定风速以上至切出风速,机组工作在恒功率控制阶段。由于风速已超过额定风速,为保持功率不超过额定值,机组控制系统通过叶片桨距角的变化,甩掉多余的风能,使功率保持在额定值附近。由于在额定风速以上通过增大叶片桨距角人为减小风能利用系数,且根据风速威布尔概率分布曲线,低风速出现的频次远高于高风速出现的频次,本文仅研究额定风速以下的风电机组的发电性能。图1和图2分别为同一风电机组在2个不同时段的风能利用系数与风速的关系图。时段1和时段2数据为10 min间隔数据,都为1423条记录。利用每条记录中的功率和风速数据根据式(1)计算得到该点的风能利用系数 Cp。

图1 机组时段1风能利用系数Fig.1 Distribution of wind power utilization coefficient during Period 1

图2 机组时段2风能利用系数Fig.2 Distribution of wind power utilization coefficient during Period 2
由于风速、风向随机变化,偏航系统、控制系统等存在偏差,即使在风速相同的情况下,风电机组发出的功率也会不同。在图1和图2中,与某一风速对应的Cp值有多个而不是一个,Cp散点呈带状分布。时段1为风电机组正常运行时的发电性能,而时段2风能利用系数明显异常偏低。
对发电性能或风能利用系数有影响的关键因素如下。
(1)风资源特性,包括风速和湍流。
由于在不同风速下风电机组的运行方式不同,对风能利用系数有很大影响,因此风速是影响因素之一。湍流反映风速在短时间内变化的情况,是由地形变化和风的不稳定性引起的,可以用湍流强度表示。湍流强度定义为瞬时风速标准差与平均风速的比值:
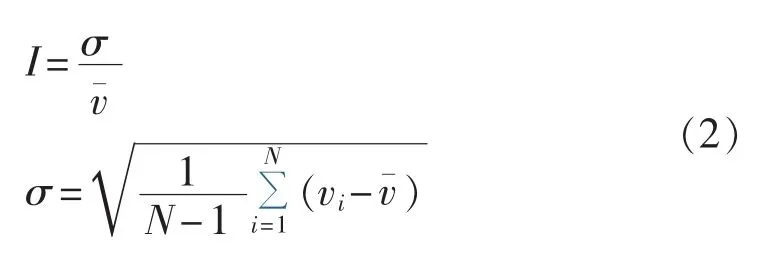
其中,vi为10 s间隔风速;为10 min间隔的平均风速;N为10 s间隔采样的风速个数。图3为时段1的湍流强度。

图3 时段1的湍流强度Fig.3 Distribution of turbulence intensity during Period 1
图3中,在低风速时风速不稳定,湍流强度较大,而在高风速时风速平稳,湍流强度较小且分布集中。当湍流强度较大时,由于风速风向变化频繁,风能不能持续作用在叶轮上转化为动能,导致机组实际输出功率往往低于测得的瞬时风功率,风能利用系数降低。在同一风电场中,由于地形对来流风的影响,地势较高或平坦处的机组的湍流强度小;而位于山脚或山谷处的机组的湍流强度与前者相比较大。因此风资源作为环境因素对风电机组发电性能有重要的影响且该影响不可控。根据风电机组所在位置的风资源特性来个性化地优化调整其运行方式和控制参数是提高机组发电性能的可行措施之一。
(2)叶轮变桨系统,包括平均桨距角、3个叶片两两之间的桨距角偏差(叶片1、2偏差,叶片2、3偏差,叶片 3、1 偏差)。
风作用在叶片上,产生气动转矩,推动叶轮旋转做功。风电机组发电性能的高低与叶轮捕捉风能的效率密切相关。叶片桨距角是指叶片剖面的翼弦与叶轮扫略平面之间的夹角,桨距角变化时能够调整叶片的迎风角度,从而增加或减少叶片产生的转矩,进而改变机组的输出功率。风电机组目前主要采用集中变桨距控制,即3个叶片的桨距角变化相同。在风电机组SCADA系统中,通常都记录3个叶片各自实际的桨距角大小。
平均桨距角为3个叶片桨距角的平均值。在额定风速以下,机组的平均桨距角应在0°附近保持不变,从而在不同风速下都能产生最大的气动转矩。但如图4所示,由于变桨距控制系统或执行机构的误差,造成额定风速以下桨距角变化,从而影响风电机组的发电性能。

图4 时段2额定风速以下桨距角变化Fig.4 Pitch angle change during Period 2 below rated wind speed
同样,由于变桨距执行机构的误差,本应该相同的3个叶片的实际桨距角之间也会不同,造成叶片1与2、叶片2与3、叶片3与1两两之间的桨距角产生误差,即桨叶不对称(blade angle asymmetry)。图5为时段2机组叶片2与3桨距角之间的偏差,该偏差不仅较大,而且偏向一侧。由于叶片之间的桨距角不同,导致某些叶片无法工作在最佳桨距角状态,叶片产生的气动转矩减小,从而影响机组的发电性能,导致风能利用系数减小。
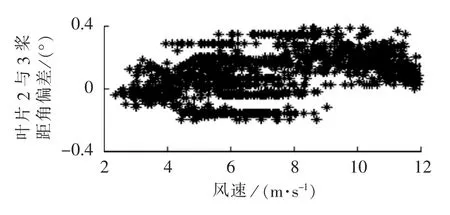
图5 时段2叶片2、3桨距角偏差Fig.5 Distribution of blade angle asymmetry between Blade 2 and Blade 3 during Period 2
(3)偏航误差。
位于机舱顶部的风向标检测风向。风向发生明显改变时,风电机组偏航系统通过偏航电机使机舱和叶轮旋转进行对风,保证叶轮与来流风向垂直,从而使叶轮捕获最大的风能。由于风向时变且偏航系统对风存在较大惯性,对风会存在一定的误差,风电机组机舱轴线和风向的夹角即偏航误差,记为θ,分布在0°附近。由于偏航误差θ的存在,叶轮捕获的风能为:

其中,Po为偏航误差为0°时捕获的风能。偏航误差造成风电机组发电能力和风能利用系数降低。图6为2个时段风电机组的偏航误差分布。

图6 时段1、2偏航误差分布Fig.6 Distribution of yaw error during Period 1 and 2
从图6可以看出,时段2的偏航误差分布明显较时段1的松散,偏航误差较大,这也是导致时段2风能利用系数偏低的重要原因。
(4)叶尖速比。
在切入风速至额定风速之间,风电机组工作在最大风能追踪模式。当风速变化时,控制系统需要调节发电机电磁转矩从而改变叶轮旋转速度,使变化的风速和叶片自身旋转速度两者合成的叶片所感受到的可视风速对叶片的攻角保持最佳位置,从而保证在不同的风速下叶轮都能获得最大的气动转矩。叶尖速比反映了叶片转速和风速的关系,记为λ,可表示为:

其中,ω为叶轮旋转角速度;R为叶轮半径;v为风速。当叶轮转速与风速的比值即叶尖速比保持不变时,可视风速对叶片的攻角也会保持不变。对于大型兆瓦级三叶片风电机组,使叶片产生最大气动转矩的最佳叶尖速比λopt通常在7~10之间。对于本文研究的机组,λopt为8.5。在切入风速至额定风速之间,风电机组控制系统在风速变化时需要不断调整叶轮转速,维持叶尖速比在最佳值附近,达到较高的发电性能。因此SCADA数据中记录的叶尖速比是风电机组控制系统运行好坏的重要标志,也反映了控制系统对发电性能的影响。图7为2个时段在某风速区间的叶尖速比值的分布。

图7 时段1、2叶尖速比分布Fig.7 Distribution of tip speed ratio during Period 1 and 2
由图7可见,时段1的叶尖速比分布在该机组的最佳叶尖速比附近;而时段2的叶尖速比分布明显偏离最佳叶尖速比,导致叶片效率和发电性能降低。因此,叶尖速比也是风电机组发电性能的重要影响因素。
2 基于高斯过程回归的风电机组发电性能建模
2.1 高斯过程回归建模
在上节分析中,风电机组的发电性能与环境因素、机组自身部件运行状态有密切关系。本文采用图1中风电机组正常运行时段1的数据和高斯过程回归方法建立机组发电性能模型。发电性能模型的输出为风电机组风能利用系数Cp的预测值,模型的输入为对发电性能有密切影响的因素,包括上节分析中的风速、湍流、叶片平均桨距角、叶片两两之间的桨距角偏差、偏航误差、叶尖速比。由于风电机组的能量来源为风,当风速改变时,风电机组的运行参数都会随风速变化,运行数据具有很强的随机性。同时由于风电机组处在户外,工作环境恶劣,昼夜温差、风沙、振动等都会导致传感器测得的运行数据存在较大的测量噪声。强随机性和高噪声是风电机组运行数据的2个重要特性,因此所选择的发电性能建模方法必须体现风电机组数据的以上2个特性。
高斯过程建模是贝叶斯方法的一种,其全部统计特性由其均值 m(x)和协方差函数 k(x,x′)确定,即:

其中,GP表示高斯随机过程。由于观测目标值y中含有观测噪声,可建立高斯过程的一般模型为:

其中,ε为独立的白噪声,符合高斯分布,均值为0,方差为,记为 ε~N(0,)。 设该高斯过程已有 N个观测样本数据对(X,y),X={x1,…,xi,…,xN},y={y1,…,yi,…,yN}。 由于 f(x)和ε 均符合高斯分布,则y同样服从高斯分布,其有限观测值联合分布的集合可形成一个高斯过程,即:
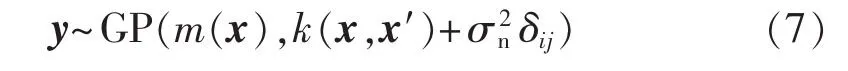
其中,δij为 Kronecker函数,当 i=j时,函数 δij=1,否则δij=0。当以矩阵形式来表示协方差函数时,有:
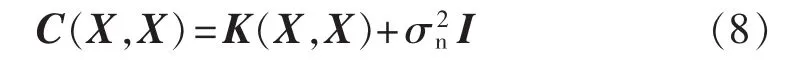
其中,C(X,X)为 N×N 阶协方差矩阵;K(X,X)为 N×N 阶核矩阵,其元素 Kij=k(xi,xj);I为 N×N 阶单位矩阵。对于符合该高斯分布的新的输入为x*及其未知输出y*,与已有样本(X,y)构成的先验联合高斯分布为[7-9]:

在已有样本数据对(X,y)和输入x*的条件下,y*的后验概率分布为:
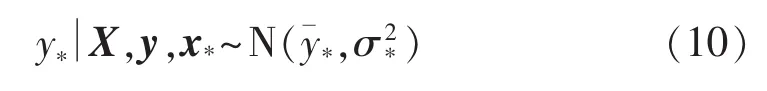
其中,为未知输出 y*的预测均值;x*)为未知输出y*的预测方差。
高斯过程建模中的协方差函数k(x,x′)是描述建模随机运行数据的重要数字特征,该函数中的参数反映了运行数据在不同输入维度上的关系紧密程度。模型中的噪声方差反映了建模数据集的噪声水平。采用高斯过程方法对运行数据建模即是确定协方差函数参数与噪声方差的过程。协方差函数确定后即可采用式(10)对新的输入进行预测。
采用高斯过程建模既可以用协方差函数来描述风电机组运行数据的随机分布规律,同时可以将数据中的噪声即有效辨识和分离,非常适用于风电机组运行数据的建模工作。与高斯过程建模相比,神经网络和支持向量机在建模时,没有考虑对信号中的噪声进行辨识和分离,直接采用含噪声的测量信号建立对象模型。在建模过程中,模型在刻画对象特性的同时,把测量噪声也固化在模型中,导致此类模型存在过学习和置信风险随模型复杂度增大而增大的问题。高斯过程应用于连续变量的建模即为高斯过程回归。
采用高斯过程对风电机组发电性能进行建模的关键是合理确定模型的输入、输出变量和模型的超参数集Θ。本文采用平方指数协方差函数:
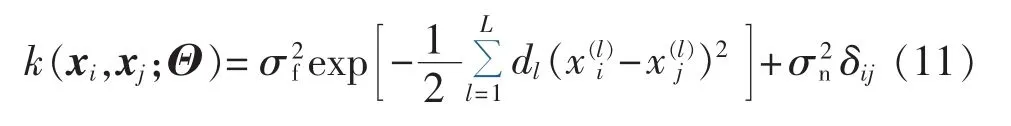
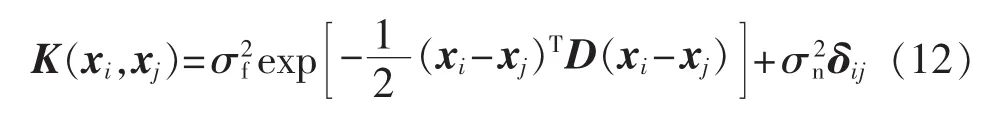
其中为向量xi∈RL的第l项;超参数集为包含协方差函数参数与噪声方差的向量,为信号方差;矩阵 D=diag(d1,d2,…,dL)表征了对应每个输入的长度尺度dl的一组集合;为噪声方差,表征了噪声水平[10-14];δij为单个 Kronecker函数;δij为由多个Kronecker函数构成的矩阵。
为了获得超参数Θ,采用对式(13)的负对数似然函数进行最小化的方法,即最大似然估计MLE(Maximum Likelihood Estimation)。

其矩阵形式如下:
负对数似然函数式(13)相对超参数Θ的一阶偏导数为:

其中,tr(·)是矩阵求迹运算,K(Θ)和Λ(Θ)简写成K和Λ。采用共轭梯度法即可求得该最大似然问题的解,即得到高斯过程模型的超参数。得到高斯过程模型的超参数后,模型建立完毕。在最大似然和共轭梯度优化的过程中,高斯过程能够根据建模数据特性自动确定信号噪声方差即信号噪声的大小,并在式(10)中用不含噪声的协方差矩阵对新的输入进行预测,从而实现噪声分离的目的。
2.2 风电机组发电性能建模
该机组时段1的运行数据用来建立发电性能模型。时段1数据共有1423条10 min间隔记录,其中前1223条记录用来进行高斯过程回归建模,剩余的200条记录用来进行模型验证。高斯过程回归建立的发电性能模型的输出为风能利用系数Cp预测值。模型的输入为第1节分析得到的发电性能的影响因素,包括每条记录中的风速、偏航误差、叶片平均桨距角以及间接计算得到的湍流、叶片两两之间的桨距角偏差、叶尖速比共8个输入。因此高斯过程发电性能模型的超参数除了信号方差和噪声方差外,还有与 8 个输入有关的 D=diag(d1,d2,…,d8)共 10个参数。采用1223个建模样本和共轭梯度法求解高斯过程模型的超参数,得到高斯过程模型的超参数见表1,其中d1(风速)表示输入量风速的长度尺度,其他类似。

表1 高斯过程发电性能模型超参数Table 1 Hyperparameters of Gaussian process power generation performance model
采用未参与建模的200条记录对已建模完毕的高斯过程发电性能模型进行验证,验证结果见图8。
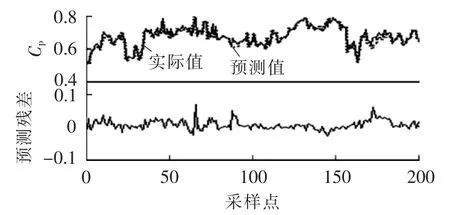
图8 高斯过程发电性能模型验证Fig.8 Validation of Gaussian process power generation performance model
图8中,实线为实际Cp值,虚线为高斯过程预测Cp值(都为归一化后的值,后同),具有较高的建模精度。将BP神经网络与高斯过程回归建模效果进行对比。BP网络的输入参数为8个,即高斯过程回归模型的输入;输出层节点数为1即预测Cp值;隐含层节点数设为20;其训练样本、验证样本与高斯过程建模相同。BP神经网络模型预测结果如图9所示。

图9 神经网络建模效果验证Fig.9 Validation of neural network model
图9中,实线为实际Cp值,虚线为神经网络预测结果。高斯过程模型和神经网络模型预测残差的方均根误差分别为0.0136和0.0237。通过对比可知,高斯过程建模具有更高的建模精度。
3 风电机组发电性能监测
发电性能模型反映了风电机组在正常运行时发电性能与多个影响因素之间的内在复杂关系。模型建立完毕后即可开始风电机组发电性能的监测工作。将新的运行数据作为发电性能模型的输入,如果模型新的输入、输出变量之间的关系与模型记忆的发电性能一致,即机组发电性能正常,模型的预测Cp值与实际Cp值之间的残差会很小,模型的预测精度很高;当机组发电性能发生改变,新的输入、输出之间的关系偏离模型记忆的发电性能特性,模型预测输出Cp值将会偏离实际Cp值,模型预测残差增大,预示机组发电性能出现异常变化。监测原理如图10所示。
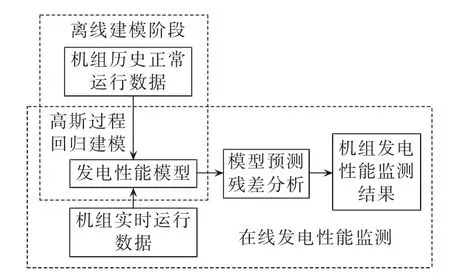
图10 风电机组发电性能监测原理Fig.10 Schematic diagram of power generation performance monitoring for wind turbine generator
选取时段2中的部分数据作为已建立的高斯过程发电性能模型的输入,模型预测结果如图11所示。

图11 高斯过程发电性能模型监测结果Fig.11 Results of power generation performance monitoring by Gaussian process model
如图1、图2所示,风电机组在运行过程中风能利用系数在0与贝兹极限之间波动,只考察个别风能利用系数自身的大小并不能反映机组发电性能的变化。通过建立风电机组正常运行时的发电性能模型,找到了风能利用系数与其多个影响因素之间的复杂联系。对发电性能的监测不是考察风能利用系数自身大小的变化,而是考察风能利用系数与其影响因素之间的关系是否改变。由于与正常时段1相比,时段2风能利用系数与其影响因素之间关系发生明显改变(如第1节分析中的偏航误差、叶尖速比),当其数据作为发电性能模型输入时,模型输出残差明显增大,如图11所示,方均根误差达到0.0498,预测精度显著下降,可检测出时段2机组发电性能出现异常变化。通过设定预测残差阈值,能够实时监测风电机组发电性能的异常变化。可以参考文献[15]采用滑动窗口残差计算和阈值设定方法来保证性能监测的灵敏度和可靠性,也可以人为设定发电性能报警阈值。当发现机组发电性能异常时,应尽快逐项检查其影响因素(如变桨系统、偏航系统和控制系统等)是否存在运行异常并及时消除。
4 结论
风电机组发电性能高低对风电场运行经济效益有重要影响。本文利用风电机组SCADA运行数据并结合运行原理,分析了对机组发电性能有密切影响的因素,包括风资源、变桨系统、偏航系统和叶尖速比。然后,采用适合风电机组数据随机性强和高噪声特点的高斯过程回归建模方法,建立了反映机组发电性能的风能利用系数和其影响因素之间复杂关系的发电性能模型。该模型能够实时监测风电机组发电性能变化。同时,如果出现风电机组发电性能降低,也可通过反推逐项分析机组发电性能的影响因素,找到导致机组发电性能降低的原因,进而加以改进,提高机组发电性能。
[1]段振云,杜坡,邢作霞.叶片安装误差对风电机组性能影响的研究[J]. 风能,2015(1):88-91.DUAN Zhenyun,DU Po,XING Zuoxia.Research of blade angle error influence on wind turbine performance[J].Wind Energy,2015(1):88-91.
[2]张治俊,李辉,陈宏文,等.双馈风电机组总体控制策略及运行性能[J]. 重庆大学学报,2011,34(7):63-68.ZHANG Zhijun,LI Hui,CHEN Hongwen,et al.Overall control strategy and operational performances of a doubly fed wind turbine generator system[J].Journal of Chongqing University,2011,34(7):63-68.
[3]鲁林平,王一平,黄群武,等.多风轮风力发电系统发电性能研究[J]. 机械设计,2015,32(2):70-74.LU Linping,WANG Yiping,HUANG Qunwu,etal.Studyon power generation performance of the MR_HAWT[J].Journal of Machine Design,2015,32(2):70-74.
[4]POURRAJABIAN A,MIRZAEI M,EBRAHIMI R,et al.Effect of air density on the performance of small wind turbine:a case study in Iran [J].Journal of Wind Engineering and Industrial Aerodynamics,2014,126(2):1-10.
[5]林鹏,赵书强,谢宇琪.基于实测数据的风电功率曲线建模及不确定估计[J]. 电力自动化设备,2015,35(4):90-95.LIN Peng,ZHAO Shuqiang,XIE Yuqi.Wind power curve modeling based on measured data and uncertainty estimation[J].Electric Power Automation Equipment,2015,35(4):90-95.
[6]赵亮,韩华玲,陈宁.基于模糊滑模控制的风电机组最大风能追踪策略[J]. 电力自动化设备,2012,32(12):74-79.ZHAO Liang,HAN Hualing,CHEN Ning.Maximum wind energy tracking based on fuzzy sliding mode control for wind power generation system [J].ElectricPowerAutomation Equipment,2012,32(12):74-79.
[7]RASMUSSEN C E,CHRISTOPHER K I.Gaussian processes for machine learning[M].Cambridge,Massachusetts,USA:The MIT Press,2005:13-19.
[8]HONG X,GAO J B,JIANG X,et al.Fast identification algorithms for Gaussian process model[J].Neurocomputing,2014,133(133):25-31.
[9]HUBER M F.Recursive Gaussian process:on-line regression and learning[J].Patten Recognition Letters,2014,45(1):85-91.
[10]孙斌,姚海涛,刘婷.基于高斯过程回归的短期风速预测[J].中国电机工程学报,2012,32(29):104-109.SUN Bin,YAO Haitao,LIU Ting.Short-term wind speed forecasting based on Gaussian process regression model[J].Proceedings of the CSEE,2012,32(29):104-109.
[11]苏国韶,赵伟,彭立峰.边坡失效概率估计的高斯过程动态响应面法[J]. 岩土力学,2014,35(12):3592-3601.SU Guoshao,ZHAO Wei,PENG Lifeng.Gaussian process based dynamic response surface method for estimating slope failure probability[J].Rock and Soil Mechanics,2014,35 (12):3592-3601.
[12]张乐,刘忠,张建强.一种改进高斯过程回归建模方法[J].华中科技大学学报(自然科学版),2013,41(10):115-118.ZHANG Le,LIU Zhong,ZHANG Jianqiang.Improved Gaussian process regression modeling method [J].Journal of Huazhong University of Science&Technology(Natural Science Edition),2013,41(10):115-118.
[13]WANG B,CHEN T.Gaussian process regression with multiple response variables[J].Chemometrics and Intelligent Laboratory Systems,2015,142:159-165.
[14]郭鹏,王雪茹.风电机组高斯过程回归塔架振动监测研究[J].动力工程学报,2015,35(5):380-386.GUO Peng,WANG Xueru.Vibration monitoring by Gaussian process regression for wind turbine tower[J].Journal of Chinese Society of Power Engineering,2015,35(5):380-386.
[15]GUO Peng,INFIELD D,YANG Xiyun.Wind turbine generator condition monitoring using temperature trend analysis[J].IEEE Transactions on Sustainable Energy,2012,3(1):124-133.
