基于改进局域Volterra自适应滤波器的风电功率混沌时间序列预测模型

王 兰，李华强，吴 星，王羽佳

（四川大学 电气信息学院 智能电网四川省重点实验室，四川 成都 610065）

0 引言

风力发电以其清洁、成本低等特点已成为一种成熟、具有规模效益的新能源利用形式。但是风电具有间歇性、波动性等特点，这使得大规模风电并网将对电网造成很大影响［1］。准确地预测风电功率，不仅能够提高风机可利用率，提高电网的经济安全运行水平，同时也可以为风电场在无风或小风情况下安排计划检修提供指导。由此可见，对风电功率进行准确的短期预测具有重要的现实意义。

混沌时间序列预测法作为揭示混沌时间序列客观规律的一种方法，已广泛应用于风电功率时间序列预测［2］。许多研究者就混沌时间序列预测法进行过研究，目前应用广泛的主要是时间序列法［3］、神经网络［4］、支持向量机［5］等方法。 时间序列法计算速度较快，但往往预测精度较低；传统的神经网络（如RBF、BP网络），学习时间太长，易陷入局部最优；最小二乘支持向量机作为支持向量机的改进，其学习时间虽有很大提高，但要求核函数必须满足Mercer定理。上述缺点均制约着这些方法在风电功率预测中的发展应用。近几年来，Volterra自适应滤波器以其训练速度快、所需样本量小等优点得到了广大学者的关注［6-7］。但Volterra自适应滤波器的预测效果易受与预测点信息不相关或对预测点贡献较小的相点影响［7］。 文献［8］采用邻近点作为训练集，建立局域支持向量机模型，证明合理筛选邻近点可提高模型的精度。针对邻近点的选择，目前的主要判据有欧氏距离［8-9］、向量夹角［10］、关联度［11］等。 欧氏距离、关联度没有考虑相点的演化规律，向量夹角没有考虑相点的当前位置，且大部分传统方法忽略了相点自身的不同坐标分量的时间次序对预测点的影响不同，易引入“伪邻近点”。

针对上述问题，本文在传统研究方法的基础上引入时间权重，提出考虑时间影响的距离与演化趋势判据，并将这2个判据进行加权处理，进一步对这2个判据的权重指标进行了探讨，根据模型精度选择最佳综合判据对相点进行筛选，并对筛选后的相点建立改进局域Volterra自适应滤波器模型，以我国某风电场的实测风电功率数据为算例，验证了本文所提方法的有效性，为风电功率的短期实时预测提供了新思路。

1 Volterra自适应滤波器

1.1 相空间重构

混沌时间理论认为混沌序列在一维空间内呈现出杂乱无章的特点，但当对此类序列进行相空间重构后，可反映出其内部规律。因此，相空间重构是分析混沌时间序列的基础。

设初始风电功率时间序列为｛x（1），x（2），…，x（N）｝，其中N为风电功率的采集点总数，相空间重构后得到相点时间序列向量为［4］：

由式（1）可以看出，对序列进行相空间重构的根本在于求出时间序列的延迟时间τ与嵌入维数m。

1.2 Volterra自适应滤波器

Volterra自适应滤波器作为自适应预测法的典型代表，其充分利用Volterra级数的高阶展开式，综合考虑混沌序列中的非线性因素，可以根据当前数据和误差不断调整模型参数，只需要少量的样本就可达到较好的精度，目前已得到广泛应用。

由于Volterra自适应滤波器的核函数的Volterra级数展开表示式为无穷级数形式，难以用于实际应用，通常采取有限截断和有限次求和形式［12］。p阶截断模型为：

其中，由Taken嵌入定理可取N1=N2=…=Np=m；（n+1）为预测值；hp（m1，m2，…，mp）为 p 阶 Volterra核；m为滤波器的输入维数，对应风电功率时间序列的嵌入维数［7］。

本文的Volterra自适应滤波器模型取p=2。此外，本文采用时间正交（TDO）自适应算法［8］作为Volterra滤波器的自适应算法。

2 邻近点的选择

Farmer和Sidorowich早已证明，在相同的嵌入维数下，局域预测法的效果比全局预测法更好［13］。本文结合局域预测法和自适应预测法的优点，使用局域预测法对相点进行筛选，再使用筛选后的邻近点作为自适应预测法的训练集，以提高Volterra自适应滤波器的精度。

对邻近点的选择不仅要从众多相点中寻找与预测点演化轨迹相似的相点，提高模型的学习性能，还要控制好邻近点的数量规模，避免增加模型复杂度，同时避免引入相关性较弱的相点影响模型精度。本文提出一种选择邻近点的新判据，避免引入传统方法中存在的“伪邻近点”。

2.1 邻近点的相似度

从时间上看，邻近点向量越靠后的坐标分量离预测点越近，其影响越大。本文提出改进欧氏距离和改进演化趋势来综合评估邻近点的坐标分量对预测点的影响。除此之外，回溯步长越小，其对预测点的影响也越大，因此，本文在改进演化趋势判据的同时对多步演化的影响力进行加权处理，得到筛选邻近点的综合判据如下。

定义一种新的运算方式：

判据1 当前预测点X（p）与相点X（i）的距离。

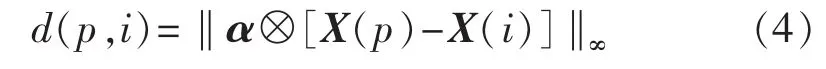
其中，α为权重向量，且对于m维向量α而言，α（1）≤α（2）≤…≤α（m），考虑到坐标分量间的间隔时间均为τ，本文取

d（p，i）越小，表明当前预测点 X（p）与相点 X（i）的距离越近。

判据2 预测点X（p）与相点X（i）间的演化发展趋势。

定义多步回溯的差值向量为：

多步回溯的预测点与相点间的方向夹角为：

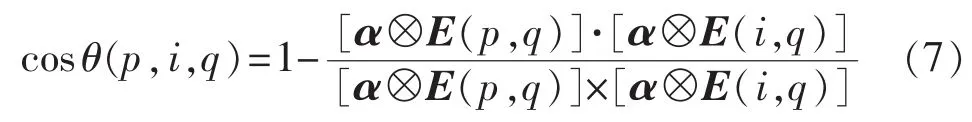
对上式进行加权，可得预测点与相点的发展趋势判据为：

其中，cosθ（p，i）是由向量间的夹角的余弦演化而来；β 为权重向量，本文取

cosθ（p，i）越小，表明当前预测点 X（p）与相点X（i）的发展趋势越接近。

综合判据 预测点X（p）与相点X（i）的相似度。

其中，γ1、γ2分别为距离指标与演化趋势指标的权重值，且 γ1+γ2=1。

η（p，i）综合考虑预测点与相点的当前距离和相点间的多步演化趋势，既考虑了相点的演化相关性，又考虑了相点各坐标在时间上的不同影响，因此能有效避开“虚伪邻近点”，选出在距离和演化趋势上均与预测点相似的邻近点，进一步提高预测精度。

2.2 邻近点集合规模控制

为了控制训练集合的规模，本文采取Hannan-Quinn准则［14］对邻近点进行进一步的筛选。

其中，K为训练集合样本个数；xj为数据的样本点；为预测结果；为样本点均值；D为常数，一般 D＞2；S为预测步数；N为拟合数据个数。当Φ（K）取得最小值时，对应的K为最佳邻近点的个数，此时认为模型在其精度和复杂度间取得了平衡。

3 算例仿真

为验证本文所提的改进风电功率预测模型的有效性，采用我国某风电场风电机组实时采样的风电功率数据作为原始数据，从2010年8月1日00:00

c.最大绝对误差MAE。到8月29日00:00的数据，每10 min取1个采样点，共4032个点，绘制风电功率时间序列图见图1。风电场的额定装机容量为46.8 MW。

图1 我国某风电场功率时间序列Fig.1 Wind power time series of a wind farm

由图1可看出，风电功率时间序列具有明显的非线性。首先对数据进行归一化处理，将数据控制在［-1，1］之间，处理方式如下：

其中，｛y（n）｝为原始序列；｛x（n）｝为归一化的时间序列；（n）为风电功率序列的平均值；max（）和min（）分别为取最大值和最小值操作。

本文采用互信息法确定延迟时间τ，用Cao法确定嵌入维数m，再采用C-C法进行验证。计算可确定风电功率时间序列的延迟时间τ＝19，嵌入维数m＝7。 互信息法、Cao法、C-C 法参见文献［15］，由于篇幅限制，本文不再赘述。此外，本文采用小数据量法计算出风电功率时间序列的最大Lyapunov指数为0.2736，证明了风电功率时间序列具有混沌特性，为使用混沌时间序列预测法进行风电功率的预测提供了依据。计算最大Lyapunov指数具体算法参见文献［15］。

使用8月1日00:00到8月24日00:00的数据对模型进行训练，使用8月24日00:00到8月28日00:00的数据进行测试，预测8月28日00:00到8月29日00:00的数据。本文采用递归多步预测。

为了定量地评估预测模型的性能，采用以下3个常用指标对模型进行评估。

a.归一化绝对平均误差NMAE。

b.归一化均方根误差NRMAE。

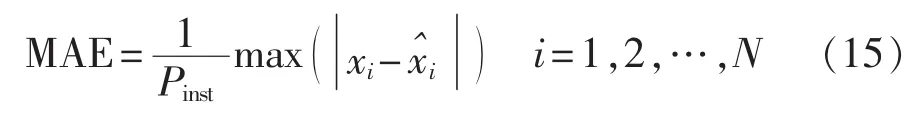
其中，xi为实际的风电功率；为对应的风电功率预测值；N为预测的时间点数，本文取为144；Pinst为风电场的装机容量。

首先，对距离与演化判据的权重进行了探讨，取γ1=0.1k（k=0，1，2，…，10）对模型进行了测试，表1列出了权重指标不同时，3个指标对预测结果的评估结果。

表1 权重指标的评估结果Table 1 Results of weighted index evaluation

由表1可知，当 γ1=0.4、γ2=0.6时，模型取得最高精度，此时归一化绝对平均误差为0.0498，归一化均方根误差为0.0619，最大绝对误差为0.2187。因此，在接下来的研究中，本文建立的改进局域Volterra模型均取γ1=0.4、γ2=0.6来构建筛选邻近点的综合判据。

此外，本文在使用综合判据对邻近点进行筛选的同时，采用常用的欧氏距离、向量夹角、关联度作为常用判据进行对比，所有筛选出的邻近点均用Volterra自适应滤波器建立局域预测模型，表2列出了采用不同判据筛选邻近点，建立模型的预测结果及建模时间。本文所有的训练和仿真均在MATLAB7.1环境下进行，采用 Intel（R） Core（TM）2 Duo 2.93 GHz双核处理器，2.0 G内存的计算机平台。

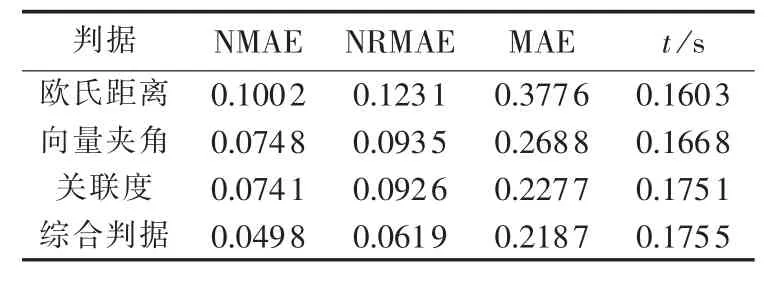
表2 采用不同判据的模型预测结果Table 2 Results of model prediction for different criterions

由表2可以看出，使用欧氏距离对邻近点进行筛选时，NMAE 为 0.100 2，NRMAE 为 0.123 1，MAE为0.3776，耗时0.1603 s，其建模速度最快，但误差远远大于其他3种判据；使用向量夹角或关联度对邻近点进行筛选时，模型的建模时间均有所增长，但模型精度均得到了一定的提升；而使用本文提出的综合判据筛选邻近点时，NMAE为0.0498，NRMAE为0.0619，MAE 为 0.2187，耗时 0.1755 s，虽然该模型的建模速度最慢，但在牺牲了较小的时间代价上其预测精度不仅比使用欧氏距离判据提高了一倍，而且比其他2种方法的预测精度高。由此可看出，综合判据既考虑了相点的演化相关性与相点的当前位置，又考虑了相点各坐标在时间上的不同影响，避开了“虚伪邻近点”，有效提高了模型的预测精度。

本文还采用以下3种预测模型与本文所提方法进行对比：第1种为时间序列法，即ARMA模型；第2种为最小二乘支持向量机（LSSVM）算法；第3种为径向基（RBF）神经网络模型。3种预测模型的预测结果及8月28日的风电功率真实值如图2所示。表3列出了3种模型的预测误差性能指标及3种模型的建模时间，其中ARMA模型的建模时间包括自相关系数与偏相关系数的计算以及定阶。

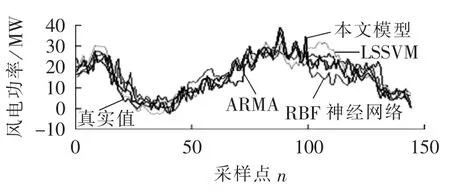
图2 风电功率实际值及各模型的预测值Fig.2 Comparison between actual and predicted wind powers for different prediction models

表3 各预测模型的误差及建模时间Table 3 Comparison of error and time consumption among different prediction models

从表3可以看出，LSSVM模型的建模时间远大于RBF神经网络模型、ARMA模型与改进局域Volterra自适应滤波器模型；同时，对比RBF神经网络模型、ARMA模型和改进局域Volterra自适应滤波器模型3种模型可发现，改进局域Volterra自适应滤波器模型的建模训练时间比RBF神经网络模型以及ARMA模型的时间短。

由图2和表3可知，使用本文提出的改进局域Volterra自适应滤波器进行风电功率的预测精度稍高于LSSVM模型，远高于RBF神经网络模型和ARMA模型。由图2可以看出，4种模型均在风电功率较低或接近满发时出现较大误差，RBF神经网络模型以及ARMA模型尤为突出，其误差明显大于LSSVM模型与改进局域Volterra自适应滤波器模型。同样可以看出，改进局域Volterra自适应滤波器模型在风电功率较低或接近满发时，仍然紧跟真实功率的变化趋势，在风电功率剧烈变化时与真实值仍十分贴合。

对比图2和表3的结果可见，改进局域Volterra自适应滤波器模型在精度上远高于RBF神经网络模型和ARMA（2，0）模型，在建模时间上远小于LSSVM模型，说明改进局域Volterra自适应滤波器模型不仅提高了风电功率预测模型的精度，还节省了模型的建模训练时间，为风电功率的实时高精度预测提供了参考。

4 结论

针对风电功率混沌序列的特点，本文提出了一种基于改进局域Volterra自适应滤波器模型的风电功率混沌时间序列预测法。对原有的邻近点判据，引入时间权重，提出考虑时间影响的改进相点距离与相点演化趋势的判据，同时将改进后的判据进行加权处理，选出使Volterra自适应滤波器模型精度最佳的权重指标；最后，对筛选出的相点建立局域Volterra自适应滤波器模型，对我国某风电场的数据进行预测分析。将本文提出的改进局域Volterra自适应滤波器模型与LSSVM模型、RBF神经网络预测模型和ARMA模型对比，实验证明本文提出的改进局域Volterra自适应滤波器预测模型不仅具有更高的精度，而且具有更快的建模速度，为风电功率短时高精度的预测在工程上的应用提供了一条可行途径。

［1］谢俊，王璐，傅旭华，等.考虑风电功率概率分布不确定性的含风电配电网无功规划方法［J］.电力自动化设备，2016，36（6）：40-47.XIE Jun，WANG Lu，FU Xuhua，et al.Reactive power planning with consideration of wind power probability distribution uncertainty for distribution network［J］.Electric Power Automation Equipment，2016，36（6）：40-47.

［2］张学清，梁军.风电功率时间序列混沌特性分析及预测模型研究［J］. 物理学报，2012，61（19）：70-81.ZHANG Xueqing，LIANG Jun.Chaotic characteristics analysis and prediction model study on wind power time series［J］.Acta Phys Sin，2012，61（19）：70-81.

［3］丁明，张立军，吴义纯.基于时间序列分析的风电场风速预测模型［J］. 电力自动化设备，2005，25（8）：32-34.DING Ming，ZHANG Lijun，WU Yichun.Wind speed forecast model for wind farms based on time series analysis［J］.Electric Power Automation Equipment，2005，25（8）：32-34.

［4］洪翠，温步瀛，林维明.基于改进OLS-RBF神经网络模型的短期风电场出力预测［J］. 电力自动化设备，2012，32（9）：40-43.HONG Cui，WEN Buying，LIN Weiming.Short-term forecasting of wind power output based on improved OLS-RBF ANN model［J］.Electric Power Automation Equipment，2012，32（9）：40-43.

［5］凌武能，杭乃善，李如琦.基于云支持向量机模型的短期风电功率预测［J］. 电力自动化设备，2013，33（7）：34-38.LING Wuneng，HANG Naishan，LI Ruqi.Short-term wind power forecasting based on cloud SVM model［J］.Electric Power Automation Equipment，2013，33（7）：34-38.

［6］MARMARELIS V Z，ZHAO X.Volterra models and three-layer perceptrons［J］.IEEE Transactions on Neural Networks，1997，8（6）：1421-1433.

［7］张家树，党建亮，李恒超.时空混沌序列的局域支持向量机预测［J］. 物理学报，2007，56（1）：67-77.ZHANG Jiashu，DANG Jianliang，LI Hengchao.Local support vector machine prediction of spatiotemporal chaotic time series［J］.Acta Phys Sin，2007，56（1）：67-77.

［8］张家树，肖先赐.混沌时间序列的Volterra自适应预测［J］.物理学报，2000，49（3）：403-408.ZHANG Jiashu，XIAO Xianci.Predicting low-dimensional chaotic time series using volterra adaptive filers［J］.Acta Phys Sin，2000，49（3）：403-408.

［9］郭创新，王扬，沈勇，等.风电场短期风速的多变量局域预测法［J］. 中国电机工程学报，2012，32（1）：24-31.GUO Chuangxin，WANG Yang，SHEN Yong，et al.Multivariate local prediction method for short-term wind speed of wind farm［J］.Proceedings of the CSEE，2012，32（1）：24-31.

［10］王桓，何怡刚，侯周国，等.基于夹角余弦的混沌局域加权线性预测算法［J］. 高电压技术，2009，35（6）：1483-1487.WANG Huan，HE Yigang，HOU Zhouguo，et al.Chaotic local adding-weight linear forecasting algorithm based on included angle cosine［J］.High Voltage Engineering，2009，35（6）：1483-1487.

［11］JIANG C，LI T.Forecasting method study on chaotic load series with high embedded dimension［J］.Energy Conversion and Management，2005，46（5）：667-676.

［12］SANDBERG I W.On volterra expansions for time-varying nonlinear systems［J］.IEEE Transactions on Circuits and Systems，1983，30（2）：61-67.

［13］FARMER J D，SIDOROWICH J J.Predicting chaotic time series［J］.Physical Review Letters，1987，59（8）：845.

［14］孟庆芳，彭玉华，曲怀敬，等.基于信息准则的局域预测法邻近点的选取方法［J］. 物理学报，2008，57（3）：1423-1430.MENG Qingfang，PENG Yuhua，QU Huaijing，et al.The neighbor point selection method for local prediction based on information criterion［J］.Acta Phys Sin，2008，57（3）：1423-1430.

［15］韩敏.混沌时间序列预测理论与方法［M］.北京：中国水利水电出版社，2007：79-91.