含2个S副间隙6-SPS机构奇异性分析

赵德胜, 吴荣军

(西安邮电大学 自动化学院, 西安　710121)



含2个S副间隙6-SPS机构奇异性分析

赵德胜, 吴荣军

(西安邮电大学 自动化学院, 西安710121)

摘要：6-SPS机构位姿矩阵采用四元数法描述，并将该矩阵和矢量坐标扩展为4维形式，推导出无间隙机构的运动方程，得到了机构运动的新型雅克比矩阵JA和JB；在此基础上，利用连续接触模型得到了两个含间隙S副共连杆和异杆时机构的运动系数矩阵。分别把各个运动系数的行列式展开，得到含间隙机构第一类奇异和第二类奇异的轨迹方程，利用MATLAB得到了机构在给定位置时的第一类位姿奇异轨迹和第二类位姿奇异三维轨迹曲面；通过将两类含间隙机构奇异轨迹曲面的比较，发现机构间隙对第二类奇异的影响大于对第一类奇异的影响；在两类奇异轨迹中，当S副异杆时，机构间隙的影响均大于S副共连杆时的影响。以无间隙机构奇异轨迹曲面上奇异点作为参考点，通过含间隙机构奇异轨迹曲面上与参考点相对应奇异点的相互比较，发现存在一个关于参考点的奇异域。

关键词：四元数； 奇异位形； 含间隙并联机构；雅克比矩阵；奇异域

并联机器人具有多自由度、大承载力、精度高等优点，在现代工业生产中得到越来越广泛的应用。奇异位形是机构的一个固有属性，当并联机构处于奇异位形时，机构自由度发生变化，给运动控制带来困难[1]。自20世纪90年代就有学者发现，并联机构的奇异位形并不只是工作空间中的一些孤立点，还找到了一系列连续变化的奇异位形，称为奇异轨迹[2-3]。一些研究者近年来对并联机构进行了深入研究，发现其雅克比矩阵行列式展开后十分复杂。国内学者基于螺旋理论建立雅克比矩阵研究了Stewart并联机构的位置奇异轨迹，得出了姿态奇异轨迹的解析表达式。但是，这种方法得出的雅克比矩阵不仅所含项数多而且含有超越项，难以求解。目前，对并联机构的奇异性研究方法还不成熟，需要从结构设计和理论创新方面进行突破[4-6]。

机构奇异位形的存在对机构的运动、受力等各个方面均产生了较大影响，严重时可能损坏机构。因此，专家们不得不提出各种免奇异研究方法。但是，很多免奇异方法没有考虑机构间隙对奇异位形的影响。机构间隙的存在不仅影响机构运动精度而且对机构的奇异位形也有较大影响。本文利用四元数法对含间隙6—SPS机构的奇异位形进行了研究。

本文出于以下两个原因只考虑2个球面副的间隙：① 在该并联机构中球面副相对其他运动副更加普遍且位于驱动支链上，对其进行研究更显一般性。② 为了简化计算和方便公式推导。

1四元数与位姿矩阵

四元数的一般形式为：

ε=ε0+ε1i+ε2j+ε3k

(1)

式中：ε,ε0,ε1,ε2,ε3∈R。采用单位四元数描述并联机构动平台的姿态，对应变换矩阵R为[12]:

(2)

将3阶变换矩阵R扩展为4阶形式：

(3)

(4)

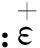
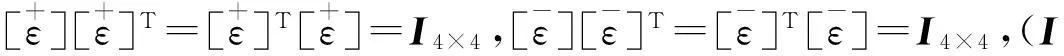
(5)

为了下文的雅克比矩阵转化方便，预定义4维矢量：h=(h1h2h3h4)T，由式(5)可得：

(6)

式中：P为动坐标系的原点O′在惯性系O-XYZ((见图1)中的位置矢量。

2无间隙机构运动学方程

为了便于分析含间隙机构奇异位形特点，首先分析无间隙机构的奇异位形，以便二者比较。

2.16-SPS机构简图及平台顶点参数

图1为该机构的机构简图，表1给出了机构各顶点在动坐标系和惯性坐标系中的坐标参数。

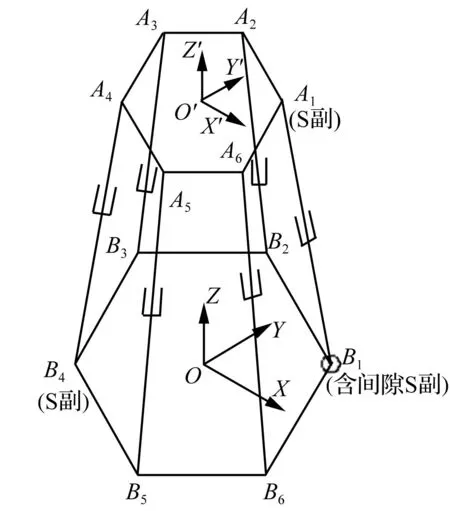
图1　6-SPS机构简图Fig.1 6-SPS parallel mechanism diagrammatic sketch

图1中：坐标系O-XYZ为惯性坐标系(定坐标系)，固联与定平台；O′-X′Y′Z′为动坐标系，固联与动平台。表1是动静平台各个顶点的X和Y轴坐标参数，是事先给定的数值；动平台各个顶点的X和Y轴坐标值由参数θ2和动平台顶点外接圆半径r2确定。静平台各个顶点的X和Y轴坐标值由参数θ1和静平台顶点外接圆半径r1确定。

表1　动静平台各顶点坐标参数

2.2运动学方程推导

在已得到动平台位姿矩阵R(式(2))的基础上，令位置矢量P=(PxPyPz)T，其中Px、Py、Pz为P在各轴的分量。则动平台和定平台对应顶点之间的连杆矢量为：

lkek=P+Rak-bk

(7)

式中：lk为连杆AkBk的长度，k=1～6；ak为动平台顶点在动坐标系中的矢量，k=1～6；bk为静平台顶点在静坐标系中的矢量，k=1～6；ek为连杆AkBk的单位矢量，k=1～6。

由式(4)和式(7)可得：

(8)

又由式(6)可得：

(9)

式中：Q是动平台在动坐标系O′-X′Y′Z′(见图1)中的位置矢量。式(7)两边点乘自身，并将顶点坐标代入可得：

2(axkbxk-aykbyk)(2ε0ε3)+2aykQy+PP-

2(axkbxk+aykbyk)(2ε1ε2)-2bxkPx-2bykPy

(10)

式中：ra为动平台各顶点矢径,ra=1.2。rb为静平

台平台各顶点矢径，rb=2(本文中动、静平台均为正六边形)。Qx、Qy、Qz为Q在各轴的分量。

由式(6)和式(9)可得：

Px=h1ε0-h0ε1-h3ε2+h2ε3

Py=h2ε0-h0ε2+h3ε1-h1ε3

Qx=h1ε0-h0ε1+h3ε2-h2ε3

Qy=h2ε0-h0ε2-h3ε1+h1ε3

又由式(10)包含6个类似方程，将表1中各顶点参数代入整理得到式(11)：

Mat1η1=Mat2η2+L

(11)

式中：

L为杆长矩阵，

在Mat2中，

由此将式(11)整理可得：

令

由此可得：

(12)

在式(12)中含有6个方程，8个输入变量。为了得到运动学运动系数方阵，又根据单位四元数的性质：

(13)

把式(12)和式(13)合并成式(14)：

(14)

对式(14)两边求导可得：

JAVε=JBVs

(15)

(16)

(17)

3含间隙机构运动学方程推导

3.1两个含间隙S副异杆

在含间隙S副B1点处建立坐标系OB1-XB1YB1ZB1(见图2)。

式中：OB1为无间隙时与B1点对应的理想顶点;O为原定平台中心;OB1b1为XB1轴最大间隙Lexmax;OB1a1为A1B1连杆最大间隙Lezmax;OB1b2、OB1b6表示YB1轴向上定平台B1B2、B6B1边长的最大间隙Leymax。

假设:

(1) 第一、第二支链的定平台S运动副含有间隙，并把各个轴向间隙矢量简化为一个无刚度连杆。

(3) 假设在三个坐标轴方向上机构间隙最大值相等，即Lexmax=Leymax=Lezmax。

(4) 两个S副在各个坐标轴方向的间隙最大值相等。

(5) 机构间隙变化速度最大值相等。由此得第一和第二连杆支链矢量方程为：

(li+lz)ei=P+Rai-(bi+le)

(18)

式中：i=1,2。

整理后可得式(19)：

(axi(bxi+lex))-ayi(byi+ley))-

2(axi(bxi+lex)-ayi(byi+ley))(2ε0ε3)+2ayiQy+PP-

2(axi(bxi+lex)+ayi(byi+ley))(2ε1ε2)-

2(bxi+lex)Px-2(byi+ley)Py

(19)

式中：i=1,2。式(19)中：等式左边系数接近于0的项被省略。

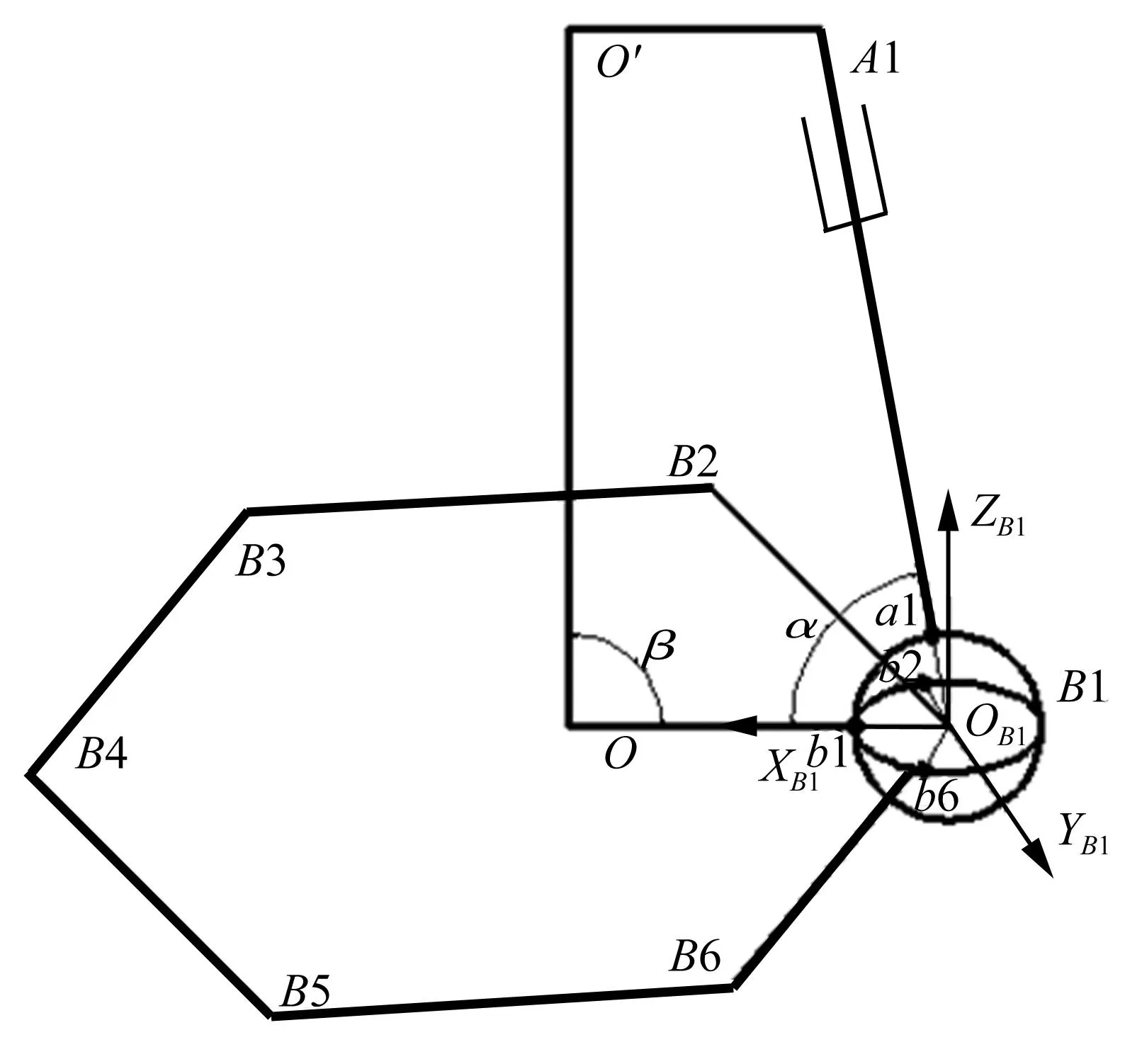
图3　含间隙运动副平面连杆机构示意图Fig.3 Mechanism with clearance diagrammatic sketch

由图3可知，Lex+Ob1=(A1B1+Lez)cosα+O′A1+OO′cosβ，两边求导得：

Ve=

JAS1Vε=JBS1Vs

(20)

式中：

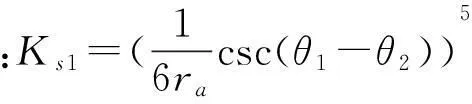
3.2两个含间隙S副共连杆

假设:

(1) 第一连杆支链的两个S运动副含有间隙(其简图见图2，把各个轴向间隙矢量简化为一个无刚度连杆。

(4) 两个S副同坐标轴方向间隙最大值相等,即Lexmax=Leymax=Lezmax。

(5) 机构各个间隙变化速度最大值相等。由此得第一连杆支链矢量方程为：

(l1+lz)e1=P+R(a1+le)-(b1+le)

(21)

整理后可得：

(ay1+ley)(by1+ley))-

(ay1+ley)(by1+ley))+

2(ax1+lex)Qx-2(by1+ley)Py+

2((ax1+lex)(bx1+lex)-

(ay1+ley)(by1+ley))(2ε0ε3)+

2(ay1+ley)Qy+PP-2((ax1+lex)(bx1+lex)+

(ay1+ley)(by1+ley))(2ε1ε2)-2(bx1+lex)Px

(22)

由式(10)、式(22)可得含间隙机构运动学方程：

JAS2Vε=JBS2Vs

(23)

式中：

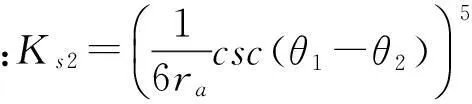
4奇异位形分析

4.1第一类奇异

4.1.1奇异轨迹曲面

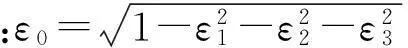
(21)

det(JA)=0的展开式可表示为：

f(U,V,W,Px,Py,Pz)=0

(22)

图4为一个给定位置时的奇异轨迹曲面。同样,根据含间隙机构的运动系数矩阵JAS1、JAs2，在机构间隙最大值相等的条件下，得到两S副异杆和共杆时的第一类奇异轨迹曲面(见图5、图6)。以图4为参考，图6的变化较大；另外，由表2、表3、表4可知，相对于表1中参考点的坐标值，表4中点的坐标值变化大于表3中的点。说明两个间隙S副异杆时对机构奇异位形影响较大。

表2　无间隙机构奇异点坐标值

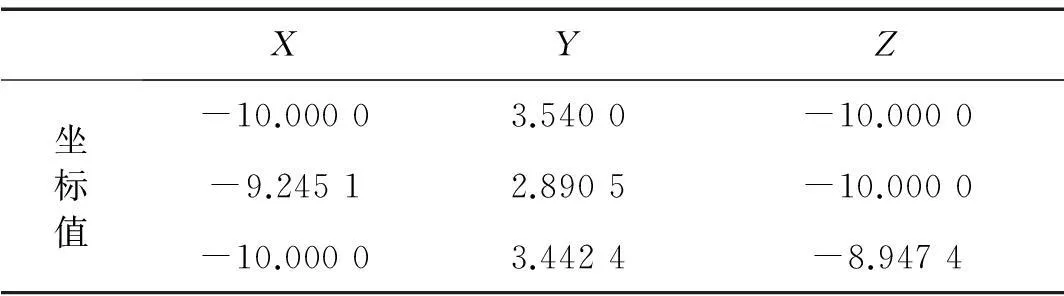
表3　含间隙S副共杆e=0.06奇异点坐标值

表4　含间隙S副异杆e=0.06奇异点坐标值

图4　Px=1，Py=2,Pz=2Fig.4 Px=1，Py=2,Pz=2

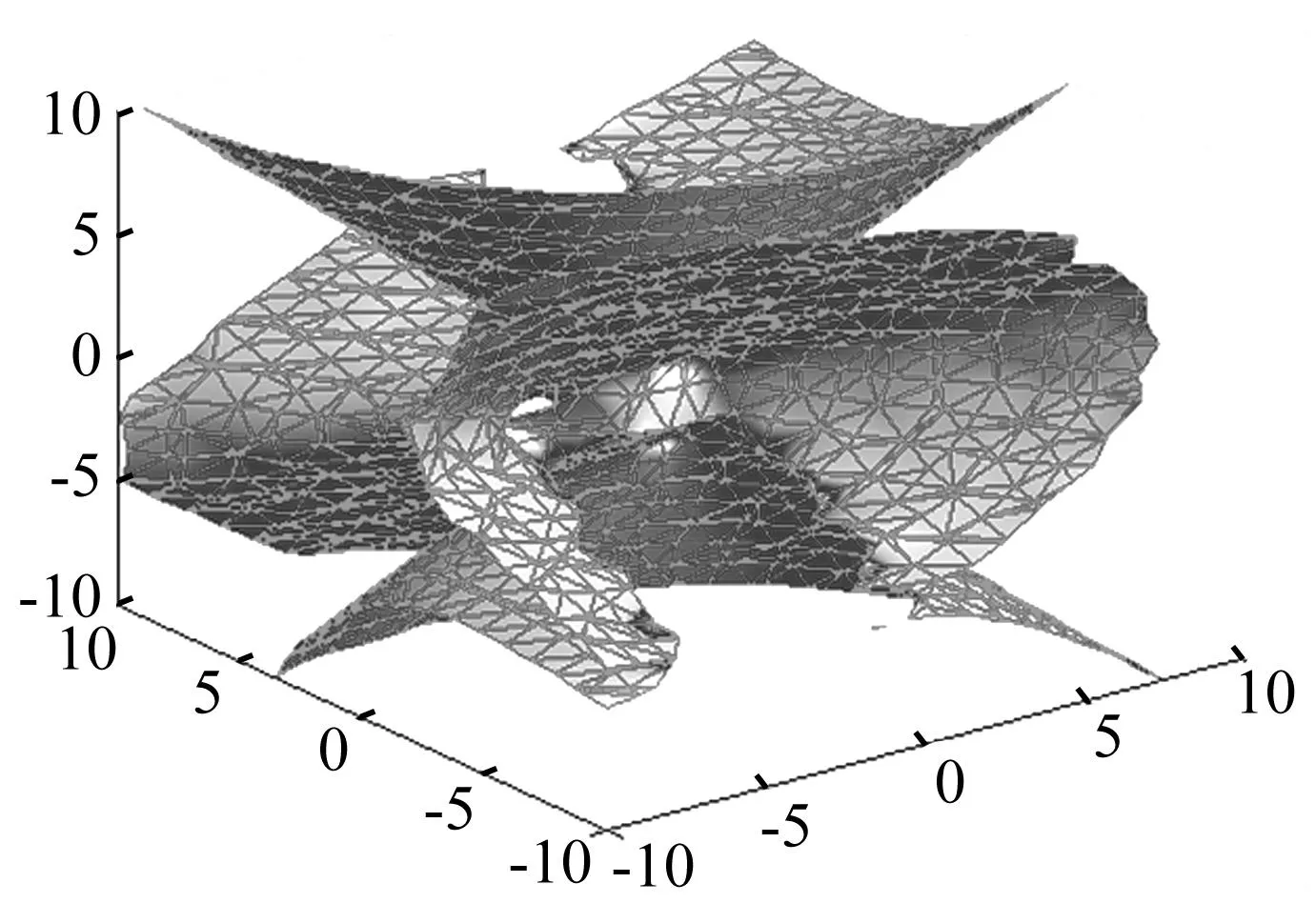
图5　含间隙S副共杆e=0.06,Px=1，Py=2,Pz=2Fig.5 S pairs with clearance in a same linkage e=0.06,Px=1，Py=2,Pz=2

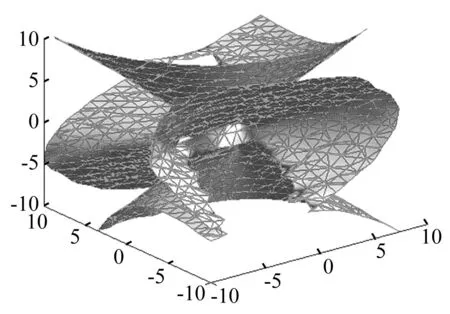
图6　含间隙S副异杆e=0.06,Px=1，Py=2,Pz=2Fig.6 S pairs with clearance in a different linkage e=0.06,Px=1，Py=2,Pz=2

4.1.2点的奇异域

取机构间隙e=0时，奇异轨迹曲面上的第一个点为参考点A。

当机构间隙e=0.06时，提取若干组奇异曲面上的与之相对应点的坐标，通过观察点的坐标值变化，发现不同曲面上的与参考点对应的点均分布在参考点A附近(见图7)，图中用黑色矩形表示点为参考点)。即存在一个包含参考点A的点奇异域。在这个区域内的任意一点，在机构运动时都可能成为奇异点(见图7、图8)。但是，S副共连杆时的奇异域基本以参考点为中心；S副异杆时参考点只是其中一个普通点。

图7　不共连杆参考点奇异域图Fig.7 S pairs with clearance in a different linkage e=0.06,the reference point’s singular area

图8　共连杆参考点奇异域图Fig.8 S pairs with clearance in a same linkage e=0.06,the reference point’s singular area

4.2第二类奇异

4.2.1奇异轨迹曲面

同样，首先研究无间隙机构的奇异轨迹曲面。当det(JA)≠0 ，det(JB)=0 时，为第二类奇异。系数矩阵JB中取θ1=π/6 、θ2=π/12。展开det(JB)=0可得第二类奇异轨迹方程。图9为给定条件下的无间隙机构奇异轨迹曲面。图10、图11是在相同条件下根据含间隙机构的运动系数矩阵JBS1和JBS2得到的含间隙机构第二类奇异轨迹曲面。

通过比较图12、图13，同样说明在第二类奇异中，相对于参考点附近也存在一个奇异域。通过提取大量不同曲面上与参考点相对应的奇异点并进行比较，两种情况下，奇异域基本以参考点为中心。另外，由图11可知，含间隙S副异杆时，间隙对奇异位形的影响较大。

4.2.2两类奇异轨迹曲面的比较

对比图5和图6、图10和图11，在机构间隙相同的情况下，图10、图11相对于图9的变化差异大于图5、6相对于图4的变化差异，说明机构间隙对第二类奇异的影响大于对第一类奇异的影响。

图9 l2=6,l4=6,l6=3Fig.9l2=6,l4=6,l6=3图10 含间隙S副共杆e=0.06,l2=6,l4=6,l6=3Fig.10Spairswithclearanceinasamelinkagee=0.001,l2=6,l4=6,l6=3图11 含间隙S副异杆e=0.06,l2=6,l4=6,l6=3Fig.11Spairswithclearanceinadifferentlinkagee=0.06,l2=6,l4=6,l6=3

图12　含间隙S副异杆Fig.12 S pairs with clearance in the different linkage

图13　含间隙S副共杆 Fig.13 S pairs with clearance in the same linkage

5结论

(1) 本文利用连续接触模型得到了由四元数表示的含间隙机构运动方程的雅克比矩阵。

(2) 通过比较含间隙机构与无间隙机构奇异轨迹曲面以及曲面上对应点的坐标值，说明机构间隙对机构的奇异位形有一定影响。

(3) 通过比较含间隙机构的第一类和第二类奇异轨迹曲面，证明机构间隙对第二类奇异的影响大于对第一类奇异的影响；并且两个S副位于不同的支链时对奇异位形的影响比位于同一支链上时影响大。

(4) 通过提取不同轨迹曲面上的对应奇异点以及对其坐标值的比较，证明在参考点附近存在一个奇异域。在奇异域内任意一点都可能产生奇异。

以上研究为机构的免奇异研究提供参考。

参 考 文 献

[ 1 ] 艾青林，祖顺江,胥芳.并联机构运动学与奇异性研究进展[J].浙江大学学报:工学版，2012,46(8):1345-1353.

AI Qing-lin,ZU Shun-jiang, XU Fang. Review of kinematics and singularity of parallel manipulator[J].Journal of Zhejiang University:Engineering Science,2012, 46(8):1345-1353.

[ 2 ] Cheng Shi-li,Wu Hong-tao, Wang Chao-kun, et al. A novel method for singularity analysis of the 6-SPS parallel mechanisms[J].Science China, 2011,54 (5):1220-1227.

[ 3 ] 吴鑫，陈美丽，张彦斌．2T1R并联机构位置及奇异性分析[J]．农业机械学报，2010，41(2)：208-213.

WU Xin，CHEN Mei-li，ZHANG Yan-bin. Analysis of position and singularity of a parallel mechanism with three degrees of freedom[J]．Transactions of the Chinese Society for Agricultural Machinery，2010，41(2)：208-213.

[ 4 ] 王庚祥，刘宏昭.考虑球面副间隙的4-SPS/CU并联机构动力学分析[J]．机械工程学报，2015,51(1)：43-51.

WANG Geng-xiang, LIU Hong-zhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance[J]．Journal of Mechanical Engineering,2015,51(1)：43-51.

[ 5 ] 李雨桐，王玉新.力作用下并联机构奇异点动态稳定性[J].机械工程学报，2013,49(3):12-18.

LI Yu-tong, WANG Yu-xin. Dynamic stability of the parallel manipulator at turning point singularities under applied loads and gravities[J].Journal of Mechanical Engineering,2013,49(3):12-18.

[ 6 ] 陈江义，郝雪清，虞启辉.含间隙铰链并联机构的动力学分析[J].郑州大学学报:工学版,2012，33(1)：98-102.

CHEN Jiang-yi, HAO xue-qin, YU Qi-hui. Dynamic analysis of parallel mechanism with clearance revolute joint[J]. Journal of Zhengzhou University:Engineering Science, 2012,33(1)：98-102.

[ 7 ] 王威，沈政，宋玉玲，等.含间隙和干摩擦的连杆机构系统动力学研究[J].振动与冲击，2015，34(18): 210-214.

WANG Wei, SHEN Zheng, SONG Yu-ling, et al. System dynamics linkage mechanism with clearance and dry friction[J].Journal of Vibration and Shock,2015,34(18): 210-214.

[ 8 ] 李保坤，曹毅，黄真，等.基于四元数的6-SPS并联机器人姿态奇异研究[J].安徽理工大学学报:自然科学版，2006，26(4):12-17.

LI Bao-kun, CAO Yi, HUANG Zhen, et al. Orientation-singularity analysis of 6-SPS parallel manipulator using unit quaternion[J].Journal of Anhui University of Science and Technology:Natural Science,2006，26(4):12-17.

[ 9 ] 周玉林，高峰.3-RRR 3自由度球面机构静刚度分析[J]. 机械工程学报, 2009, 45 (4): 25-31.

ZHOU Yu-lin, GAO Feng. Stiffness analysis of spherical parallel mechanism 3RRR with 3 DOF[J].Journal of Mechanical Engineering, 2009, 45 (4): 25-31.

[10] 赵德胜，张雪，李彩琴.一种新型助力机器人奇异位形分析[J].机械传动，2013,37(10)：82-85.

ZHAO De-sheng, ZHANG Xue, LI Cai-qin. Analysis of singularity of a novel powered robot[J].Journal of Mechanical Transmission,2013,37(10):82-85.

[11] 赵德胜，李彩琴，张雪.间隙对曲柄滑块机构灵敏度的影响研究[J].西安邮电学院学报，2011,16(5)：98-100.

ZHAO De-sheng, LI Cai-qin, ZHANG Xue. Influence of clearance on sensitivity of crank-slider mechanism[J].Journal of Xi’an University of Posts and Telecommunications,2011,16(5):98-100.

[12] 贾书惠.刚体动力学[M].北京：高等教育出版杜，1987.

Singularity analysis for a 6-SPS mechanism with 2 S-pairs containing clearance

ZHAODe-sheng,WURong-jun(School of Automation, Xi’an University of Posts & Telecommunications, Xi’an 710121, China)

Abstract:The pose matrix of a 6-SPS mechanism was described with the quaternion method. The matrix and vector coordinates were expanded into a 4-dimensional form to derive the motion equations of the mechanism without clearance. Then, the novel kinematic Jacobi matrixes JA and JB of the mechanism motion were achieved. On this basis, the movement coefficient matrixes of two S-pairs co-linkage and a different-linkage mechanism were derived with the continuous contact model. Determinants of movement coefficients were expanded, respectively. Subsequently, the trajectory equations containing the first category of singularity and the second category of singularity of mechanisms containing clearance were derived, respectively. Using MATLAB software, the three-dimensional track surfaces of the first category and the second category of pose-attitude singular trajectories at a given location of the mechanism were obtained. The comparison between two types of singularity trajectory surfaces of mechanisms containing clearance showed that the influence of mechanism clearance on the second category of singular it is greater than that on the first category; among the two types of singularity tracks, the influence of mechanism clearance in different-linkage S pairs is greater than that in co-linkage S pairs; the singular point on the trajectory surface of a mechanism without clearance is taken as a reference point, comparing the singular points on the singularity trajectory surface of a mechanism containing clearance corresponding to the reference point, a singular area with respect to the reference point can be found.

Key words:quaternion;singularity; parallel mechanism with clearance; Jacobi matrix; singular area

中图分类号:THl12

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.020

收稿日期：2015-08-07修改稿收到日期：2015-09-28

基金项目：陕西省教育厅2014科学研究计划基金资助项目 (14JK1655)

第一作者 赵德胜 男，讲师，博士，1974年生