基于递归希尔伯特变换的振动信号解调和瞬时频率计算方法

胡志祥， 任伟新

(合肥工业大学 土木与水利工程学院，合肥　230009)



基于递归希尔伯特变换的振动信号解调和瞬时频率计算方法

胡志祥， 任伟新

(合肥工业大学 土木与水利工程学院，合肥230009)

摘要：精确地提取振动信号的瞬时幅值和瞬时频率对结构的参数识别和健康监测有重要作用。希尔伯特变换是一种常用的信号解调及瞬时频率计算方法，但在信号不满足Bedrosian乘积定理的条件时会造成较大误差。针对这一问题，提出了一种递归希尔伯特变换方法，用前一步希尔伯特变换计算出的纯调频信号作为新的信号，递归地使用希尔伯特变换以进行信号解调，理论分析表明递归希尔伯特变换能够快速地收敛。最后采用仿真信号对比了递归希尔伯特变换与单次希尔伯特变换、经验调幅调频分解及Teager能量算子法在信号解调及瞬时频率计算中的结果，结果表明了递归希尔伯特变换方法的实用性及精确性。

关键词：振动信号; 瞬时频率; 信号解调; 希尔伯特变换; 经验调幅调频分解

振动信号蕴涵了动力系统当前的状态信息，是结构健康监测系统需要监测的重要数据。对线性时不变系统，常用基于傅里叶变换的频谱分析获得各阶振动频率；而对非线性或时变结构，傅里叶变换的运用受到局限[1]。为此，众多学者提出使用时频分析方法来进行结构模态参数识别。

常用的时频分析方法包括两类：第一类是傅里叶变换的发展，如短时傅里叶变换、小波变换、同步挤压小波变换、S变换等，这些方法能部分地克服傅里叶变换的缺点，在信号处理领域得到了广泛的应用，但都是用预先设定的基函数来表达原始信号，存在自适应性不足、时频分辨率低的问题[2-6]；第二类是基于信号分解的方法，如希尔伯特振动分解、广义解调、迭代希尔伯特变换、希尔伯特-黄变换等，先将复杂信号分解为许多单分量信号，再计算各单成分信号的瞬时幅值和频率，这几种分解方法各自有不同的适用范围，其中希尔伯特-黄变换应用最为广泛[7-10]。

Huang等创造性地提出了经验模式分解(Empirical Mode Decomposition,EMD)方法将复合信号分解为一系列本征模态函数(Intrinsic Mode Func-tion,IMF)，再利用希尔伯特变换计算各本征模态函数的幅值函数与瞬时频率，此即希尔伯特-黄变换[10]。经验模式分解没有使用预设的基函数，而是取决于信号本身的特征，因而比较适合非线性非平稳信号分析。但是当IMF不满足希尔伯特变换Bedrosian乘积定理的成立条件时，利用希尔伯特变换求本征模态函数的幅值和频率将会存在误差[11-12]。Huang等[13]为解决这一问题提出了经验调幅调频分解方法。张亢等[14]提出用分段波形的方法来计算单分量信号的瞬时频率。经验调幅调频分解受到样条曲线拟合误差的影响，并且样条曲线可能与信号本身相割而使最终结果在部分区间取值>1(或<-1)，将影响后续的频率计算[15]。而分段波形法适用于幅值波动很小的情况，当相邻半波内信号的幅值相差较大时，用阶梯状的不连续函数替代信号幅值函数是不合理的。Teager能量算子法也常用于信号解调与瞬率估计，但只适用于对幅值、瞬时频率变化缓慢的情况[16]。

本文提出一种基于递归希尔伯特变换的单分量信号解调和瞬时频率计算方法，用前一步希尔伯特变换获得的纯调频函数作为新的信号，递归地使用希尔伯特变换计算新的纯调频信号。理论分析发现该递归过程收敛迅速，最后得出的纯调频信号有两个特点：① 零点与原信号位置相同；② 其希尔伯特变换与其正交信号相等。递归希尔伯特变换不要求幅值函数与振荡项频谱互不重叠，因此在信号解调方面有更大的适用范围。而所得纯调频信号零点位置与原信号相同，可使求得的瞬时频率能够接近真实瞬时频率。最后通过算例比较了基于递归希尔伯特变换的方法与单次希尔伯特变换、经验调幅调频分解及Teager能量算子法在信号解调及瞬时频率计算方面的结果，分析结果表明了递归希尔伯特变换的实用性及精确性。

1递归希尔伯特变换

对信号x0(t)进行希尔伯特变换即计算x0(t)与1/πt的卷积，其公式为

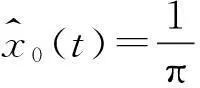
(1)

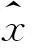
(2)

即解析函数的虚部是其实部的希尔伯特变换。该解析函数还可以表示为

z0(t)=A0exp(-jφ0)

(3)

其中

(4)

(5)

因此，可将原信号表示为幅值函数A0和纯调频信号cosφ0的乘积

x0(t)=A0cosφ0

(6)

若以纯调频函数x1(t)=cosφ0作为新的信号，并对其进行希尔伯特变换，可得到新的幅值函数和纯调频信号。不断重复进行递归计算，递归公式为

(7)

(8a)

(8b)

在递归过程中，每次得到的新信号形状不断变化，直到幅值函数An趋于1，该递归过程的收敛性在下一节进行分析。xN+1(t)=cosφN为递归终止时得到的纯调频信号，它的希尔伯特变换与其正交信号相等，即

H[xN+1(t)]=H[cosφN]=sinφN

(9)

综合所有的递归步骤，可将原信号表示为幅值函数与振荡项的乘积

(10)

可见，利用递归希尔伯特变换可将原信号分解为幅值函数和纯调频函数两部分，实现信号解调。容易证明，纯调频信号cosφN具有以下性质：

(1) cosφN的零点与原信号x0(t)的零点位置相同；

(2) cosφN的希尔伯特变换与其正交信号sinφN相等，而函数zN=cosφN+i·sinφN为解析函数。

2收敛性分析

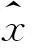
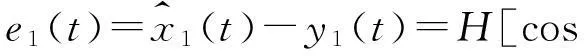
(11)

令复信号z1(t)=cosφ0+i·sinφ0，并设其傅里叶变换为W1(ω)。根据Nuttal定理[16]，正交误差函数的总能量可下式给出

(12)

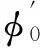
对x1(t)进行希尔伯特变换，其幅值可由下式计算

(13)

推导中利用了式(11)中正交误差函数的定义，进一步利用泰勒级数公式，并忽略高次项，可得

A1≈1+e1sinφ0

(14)

因此，进行第二次希尔伯特变后可得到新的纯调频信号x2(t)=cosφ1及其正交信号y2(t)=sinφ1，根据式(11)和式(14)可知

(15)

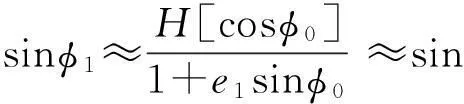
(16)

最后，再次计算x2(t)的希尔伯特变换，注意到e1为慢变函数，近似地利用Bedrosian乘积定理[11]，可得

(17)

根据式(16)和式(17)，可得出x2(t)对应的正交误差函数，即

e2=Hcosφ1-sinφ1≈

(18)

可见，每一步递归希尔伯特变换使所得的纯调频信号对应的正交误差函数取值减半。尽管在推导过程中采用了一些近似处理，两相邻递归步骤得到的纯调频信号分别对应的正交误差函数的取值不一定正好相差2倍，但收敛的趋势是显而易见的。利用式(12)，设各递归步骤中en(t)的能量为En，以rn作为正交误差函数能量递减的指标，则

rn=En/En+1

(19)

后文算例将通过En和rn的变化来考察递归过程的收敛情况。

3仿真信号分析

为验证递归希尔变换在信号解调及瞬时频率估计方面的性能，将以下信号作为待处理信号：

信号1:x1=[1+0.1cos(2πt)]cos[4πt+

sin(0.5πt)]

信号2:x2=[2+0.2cos(6πt)]cos[4πt+

sin(0.5πt)]

显然，信号1和信号2中振荡项相同，瞬时频率皆为f=2+0.25cos(0.5πt)，而两信号幅值函数不同。与振荡项相比，信号1的幅值函数为慢变函数，而信号2的幅值函数包含快变成分。因此，单次希尔伯特变换可分离信号1的幅值函数和振荡项，但不能成功地对信号2进行解调。图1给出了几种信号解调方法分解出的幅值函数，并与实际幅值函数(Truth)进行了对比，图中采用HT(Hilbert Transform)表示单次希尔伯特变换方法、EAMFMD(Empirical Amplitude Modulation Frequency Modulation Decomposition)表示经验调幅调频分解方法、TEAGER表示Teager能量算子法、RHT(Recursive Hilbert Transform)表示递归希尔伯特变换法(无特殊说明，下同)。图2给出了上述解调方法计算出的瞬时频率，并与实际瞬时频率进行了对比。

为定量说明不同方法对信号幅值和瞬时频率的识别性能，定义误差指标为

(20)

式中：aI为识别出的物理量(幅值或频率)，a为实际物理量。识别结果与真实结果越接近，误差指标值越小。表1给出了不同计算方法得到的幅值函数和瞬时频率识别对应的误差指标。

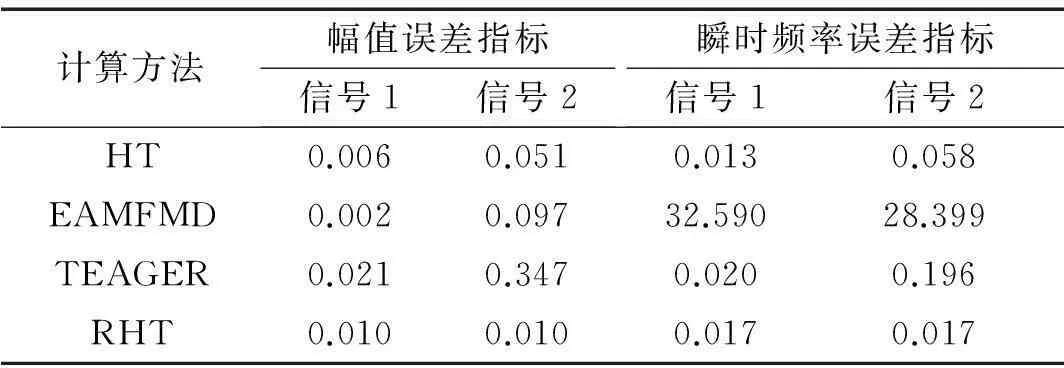
表1　幅值和频率识别的误差指标

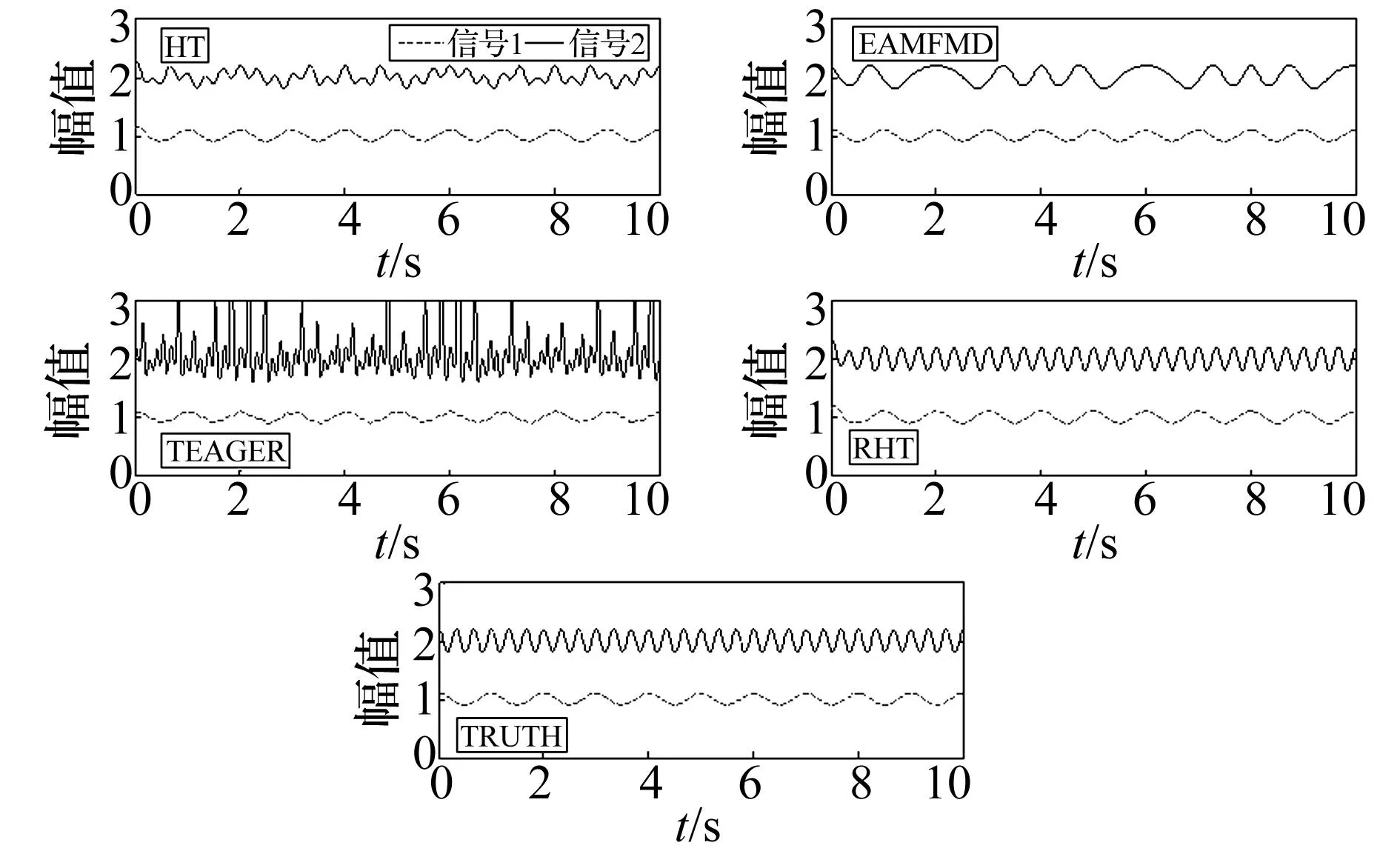
图1　不同方法计算信号1和信号2的幅值函数对比Fig.1 Comparison of the amplitude functions of signal 1 and signal 2 by different methods

图2　不同方法计算信号1和信号2的瞬时频率对比Fig.2 Comparison of the instantaneous frequencies of signal 1 and signal 2 by different methods

对于信号1，RHT和HT方法计算的幅值函数误差指标分别为0.006和0.010，瞬时频率误差指标分别为0.013和0.017，这表明计算值与实际值都比较接近。瞬时频率在信号端部包含计算误差，这是希尔伯特变换的端部效应造成的。实际应用中可通过信号镜像或延拓的方法抑制端部效应造成的误差。采用EAMFMD方法所得的幅值函数在信号端部包含较大误差，这是样条插值在信号端部不稳定导致的；EAMFMD方法估算的幅值与实际值比较接近；由于信号瞬时频率时采用反余弦法，而解调所得的纯调频函数极值点不一定为1或-1，使计算出的瞬时频率在极值点处有较大偏差，使瞬时频率误差指标高达32.590，实际使用中必须进行滤波处理。TEAGER方法所得幅值函数与实际值接近，但包含高频误差，同时瞬时频率计算结果与实际瞬时频率起伏趋势相同，但误差指标大于HT和RHT方法所得结果。事实上，只有在信号幅值和频率都为常数的情况下TEAGER方法才能计算出准确结果，虽然幅值和频率为时变函数但变化较慢时该方法仍可使用，但本文算例表明该方法并不适用于解调幅值函数和瞬时频率随时间快速变化的信号。

信号2的幅值函数含有高频振荡成分，利用HT方法不能有效解调此类信号。HT方法所得信号幅值和瞬时频率与实际幅值和瞬时频率都相差很大，误差指标分别增至0.051和0.058。EAMFMD和TEAGER方法得出的幅值和瞬时频率误差都更大。所以，HT、EAMFMD和TEAGER方法都不能有效分解信号2。由计算结果可知，只有RHT方法能有效地解调信号2，误差指标与信号1计算结果相同，这体现了RHT方法的稳定性，也表明RHT不受Bedrosian乘积定理成立条件的限制，幅值包含高频振荡成分时也能有效进行信号解调。

为验证递归希尔伯特变换的收敛性及第3节提出的瞬时频率计算方法，考察具有时变瞬时频率的纯调频信号x=cos[10πt+9sin(πt)]，其瞬时频率f=5+4.5cos(πt)，fmax=9.5 Hz，fmin=0.5 Hz。对该信号进行递归希尔伯特变换，根据式(12)和式(19)，可以计算出每次递归过程中的正交误差函数的能量En及递减指标rn。图3和图4分别给出了En和rn的变化趋势。正交误差函数的能量En随递归次数的增大而减小，而在前16步递归过程中，递减指标rn取值约等于2，随后递减指标rn快速趋近1，但保持rn≥1。考虑到正交误差函数的能量En在16步递归计算后只有5.8×10-9，此时的正交误差函数可忽略不计。由此可知，本例中递归希尔伯特变换的收敛速度较快，在实际计算时可根据数据长度及精度需求合理选择递归步数。

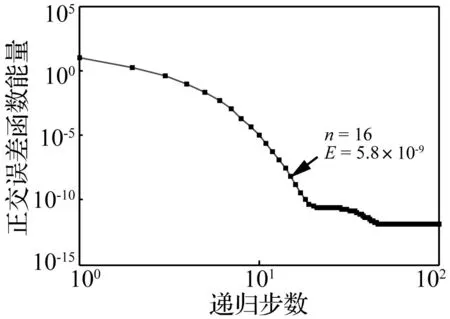
图3　正交误差函数能量变化趋势Fig.3 Variation trend of the energy in the quadrature error signal

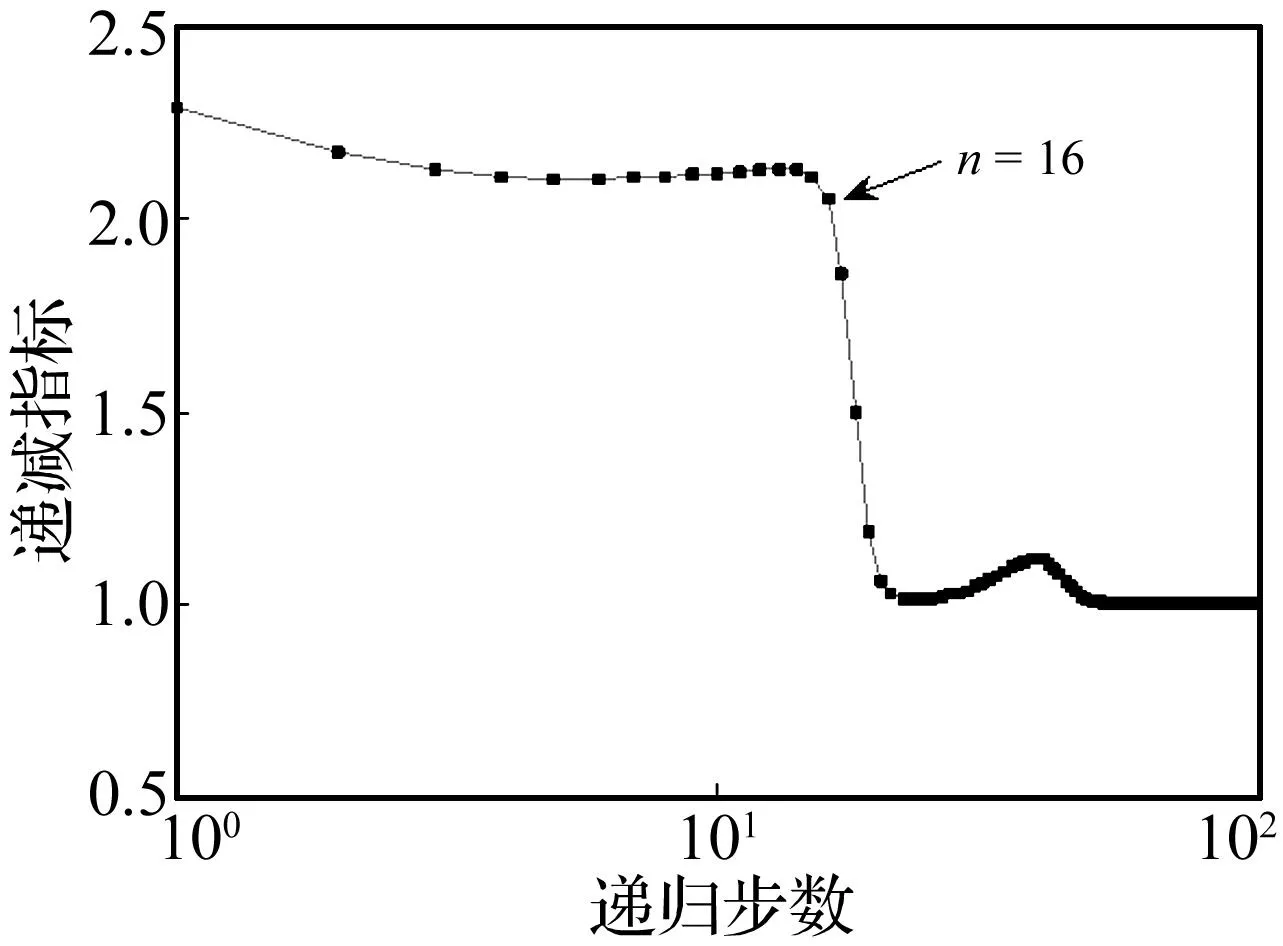
图4　递减指标变化趋势Fig.4 Variation trend of the declining indicator

4结论

提出了一种基于递归希尔伯特变换的信号解调及瞬时频率计算方法，与单次希尔伯特变换、经验调幅调频分解及Teager能量算子法等相比，具有一定的优越性。主要结论有：

(1) RHT递归计算得到的信号具有零点与原信号相同、其希尔伯特变换与正交信号相等的特点。

(2) RHT方法可用于信号解调，不受Bedrosian定理成立条件的限制，可提取包含高频成分的幅值函数，扩展了希尔伯特变换的应用范围。

(3) 理论分析及算例表明RHT具有较好的收敛性，正交误差函数的能量快速下降。

总之，递归希尔伯特变换是对希尔伯特变换这一应用广泛的信号处理方法的一个扩展。对任意给定的信号，利用RHT可以计算出零点与它相同、且希尔伯特变换与正交信号相等的纯调频信号。尽管本文对RHT方法进行了一定的理论与实例探讨，但还有较多问题值得研究，例如RHT收敛结果唯一性的证明、RHT在解析信号构造方面的应用等，希望这些问题能引起更多学者关注。

参 考 文 献

[ 1 ] 高维成, 刘伟, 邹经湘. 基于结构振动参数变化的损伤探测方法综述[J]. 振动与冲击, 2004, 23(4):1-7.

GAO Wei-cheng, LIU Wei, ZOU Jing-xiang. Damage detection methods based on changes of vibration parameters: A summary review[J]. Journal of Vibration and Shock, 2004, 23(4): 1-7.

[ 2 ] Qian S, Chen D. Joint time-frequency analysis[J].IEEE Journals and Magazings, 1999, 16(2):52-67.

[ 3 ] Ruzzene M, Fasana A, Garibaldi L, et al. Natural frequencies and dampings identification using wavelet transform: Application to real data[J].Mechanical Systemsand Signal Processing, 1997, 11(2):207-218.

[ 4 ] Wang Chao, Ren Wei-xin, Wang Zou-cai, et al. Instantaneous frequency identification of time-varying structures by continuous wavelet transform[J].Engineering Structures, 2013, 52:17-25.

[ 5 ] Ditommaso R, Mucciarelli M, Ponzo F C. Analysis of non-stationary structural systems by using a band-variable filter[J]. Bulletin of Earthquake Engineering,2012,10(3):895-911.

[ 6 ] Daubechies I, Lu J, Wu H. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J].Applied and Computational Harmonic Analysis, 2011, 30(2):243:361.

[ 7 ] 朱可恒,宋希庚, 薛冬新. 希尔伯特振动分解在滚动轴承故障诊断中应用[J]. 振动与冲击,2014,33(14):160-164.

ZHU Ke-heng, SONG Xi-geng, XUE Dong-xin. Roller bearing fault diagnosis using Hilbert vibration decomposition[J]. Journal of Vibration and Shock, 2014, 33(14): 160-164.

[ 8 ] 程军圣,杨宇,于德介.基于广义解调时频分析的多分量信号分解方法[J].振动工程学报,2007,20(6):563-569.

CHENG Jun-sheng, YANG Yu, YU De-jie. A multi-component signal decomposition method based on the general ized demodulation time-frequency analysis[J]. Journal of Vibration Engineering, 2007, 20(6): 563-569.

[ 9 ] Qin Yi, Qin Shu-ren, Mao Yong-fang. Research on iterated Hilbert transform and its application in mechanical fault diagnosis[J].Mechanical Systems and Signal Processing, 2008, 22(8):1967-1980.

[10] Huang N E, Shen Z, Long S R,et al. The empirical mode decomposition and Hilbert spectrum for nonlinear andnonstationary time series analysis[J].Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences, 1998, 454(1971):903-995.

[11] Bedrosian E. A product theorem for Hilbert transforms[J].Proceedings of IEEE, 1963, 51(5): 868-869.

[12] Picinbono B. On instantaneous amplitude and phase of signals[J].IEEE Transactions on Signal Processing, 1997, 45(3): 552-560.

[13] Huang N E, Wu Z. A review on Hilbert-Huang transform: method and its applications to geophysical studies[J].Reviews of Geophysics,2008, 46(2):1-23.

[14] 张亢, 程军圣, 杨宇,等. 基于分段波形的信号瞬时频率计算方法[J].湖南大学学报:自然科学版, 2011, 38(11): 54-59.

ZHANG Kang, CHENG Jun-sheng, YANG Yu, et al. A piece-wise based signal instantaneous frequency computing method[J]. Journal of Hunan University:Natural Sciences, 2011, 38(11): 54-59.

[15] 戴豪民, 许爱强. 瞬时频率计算方法的比较研究和改进[J].四川大学学报:自然科学版, 2014,51(6):1197-1204.

DAI Hao-min, XU Ai-qiang. Comparative research and improvement on the calculation method of instantaneous frequency[J]. Journal of Sichuan University:Natural Sciency Edition, 2014, 51(6):1197-1204.

[16] Alexandros P, Petros M. A comparison of the energy operator and the Hilbert transform approach to signal and speech demodulation[J].Signal Processing,1994,37(1):95-120.

Vibration signal demodulation and instantaneous frequency estimation based on recursive Hilbert transformation

HUZhi-xiang,RENWei-xin(School of Civil Engineering, Hefei University of Technology,Hefei 230009, China)

Abstract:Accurately extracting instantaneous amplitude and instantaneous frequency is important in structure parametic identification and health monitoring. Hilbert transformation is one of the most commonly used methods for signal demodulation and instantaneous frequency computation. However, it may cause larger errors when vibration signals do not satisfy the conditions of Bedrosian prodact theorem. Aiming at this problem, a recursive Hilbert transformation method was proposed. With this method, a pure frequency modulation signal derived in the previous step was taken as a new signal, it was modulated using Hilbent transformation recursively. The theoretical analysis showed that the recursive HirBert transformation can converge rapidly. The proposed method was compared with Hilbert transformation, the empirical AM-FM decomposition, and Teager energy method for simulated signal demodulation and instantaneous frequency computation. The results showed that the recursive Hilbert transformation.

Key words:vibrating signal; instantaneous frequency; signal demodulation; Hilbert transformation; empirical AM-FM decomposition

中图分类号:TH165.3； TN911.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.006

通信作者任伟新 男，博士，教授，1960年生

收稿日期：2015-06-25修改稿收到日期：2015-10-23

基金项目：国家自然科学基金(51408177);中国博士后科学基金(2014M551802)

第一作者 胡志祥 男，博士，讲师，1985年生