基于小波包变换和时变频率的结构地震损伤评估

何浩祥， 陈　奎， 闫维明

(1．北京工业大学 工程抗震与结构诊治北京市重点实验室，北京　100124;2．首都世界城市顺畅交通北京市协同创新中心，北京　100124)



基于小波包变换和时变频率的结构地震损伤评估

何浩祥1,2， 陈奎1， 闫维明1,2

(1．北京工业大学 工程抗震与结构诊治北京市重点实验室，北京100124;2．首都世界城市顺畅交通北京市协同创新中心，北京100124)

摘要：基于频率变化的结构地震损伤评估方法具有机理明确和精度较高等特点，但传统信号分析方法在时频分辨率上不能同时满足精度要求，导致时变频率不能直接从响应信号中精确获取，影响频率法损伤评估的应用。依据时频边缘条件提出时频谱分析精度评价标准，通过对比不同的信号分析方法，确认具有特定基函数的小波包变换是获取精确时变功率谱的有效工具;提出基于小波包脊的时变频率提取方法，在此基础上依据结构频率的变化可计算结构时变损伤指标，并最终实现结构多维地震损伤评估。算例表明基于小波包变换和时变频率的结构地震损伤评估方法可以较准确地反映结构的整体损伤演变过程和最终损伤程度;应用该方法时仅需结构的位移时程，在结构动力分析、抗震验算及实际结构的震害评估中均具良好的适用性。

关键词：地震；损伤评估；小波包变换；时变频率；时变功率谱

结构损伤可定义为结构整体或某些部分在材料和几何性能上的变化，工程结构在长期使用过程中会因各种自然及人为因素的作用而不可避免地发生损伤。由于环境变化和构件退化疲劳锈蚀等因素导致结构损伤具有缓慢积累的特点，通常可通过长期监测其演变实现损伤评估。地震等自然灾害在很短时间内就会对结构造成较严重损伤，具有显著的时变性和非平稳性。地震中结构一般将进入弹塑性状态，且其动力性能不断退化和波动，结构动力响应信号既包含结构自身动力特性，同时又蕴含丰富的地震动时频信息[1]。目前，结构地震损伤的评估很难在地震过程中在线实现，通常只能通过现场调查或对地震当时及随后的响应信号进行动力特性分析完成，并不能充分反映结构的损伤过程和细节，因此评估结构地震损伤及评定的研究意义重大且仍需不断发展和完善。目前，构件层次上的损伤评估模型主要包括基于滞回耗能、变形以及变形和耗能双变量的模型。结构整体层次上的损伤评估模型主要包括基于整体变形、整体刚度或自振周期以及整体耗能模型。目前大部分损伤评估模型均存在以下问题[2-4]：① 大部分模型是性能参数的简单统计叠加或经验组合，缺乏明确的物理意义；② 合理的损伤指标应该严格控制在[0，1]，但由大部分模型计算得到的损伤指标>1，这影响了震害较严重的结构评估精度；③ 震害模型考虑的性能参数不能只在模拟分析中获得，应通过实测信号获取且反映结构在地震过程的时变损伤特征，且计算应简便可靠；④ 研究适合整体结构损伤程度评估的震害指标实用计算模型将更具工程实践意义，基于整体结构刚度退化或模态变化的震害指标模型将更具优越性, 但尚未得到地震工程界足够的重视。

近年来，随着结构损伤识别理论和现代信号分析技术的发展，通过时变参数在线识别或非平稳信号时频分析直接获得结构时变频率从而判断结构损伤程度的方法不断成熟和发展。基于广义卡尔曼滤波、序贯非线性最小二乘法和贝叶斯估计等算法可实现简单结构的线性响应预测、反演和参数实时识别[5-6]，但限于算法能力以及计算规模，此类方法暂时不能完全实现多自由度结构的动力参数快速变化识别。在时频分析法中，比较常用的是通过对结构动力响应信号进行连续小波变换，之后利用小波系数模极大值提取小波脊从而识别时变频率[7]。但由于结构响应是典型的窄带随机过程，频带干扰较严重，传统的小波变换也较难同时满足时频两域的分辨率要求，导致识别结果中常出现只能识别某阶频率、部分时刻识别值缺失或频率增大等现象。尽管诸如基于小波传递函数和基于小波能量传递函数谱识别时变频率的改进方法被提出[8]，但效果仍不明显。一些研究者提出了利用以Hilbert-Huang变换(Hilbert-Huang Transform,HHT)为基础的经验模态分解识别结构瞬时频率的方法[9-10]，但经验模态分解缺乏严密的数学基础，频率分辨率不均匀，且不能保证其各分量严格正交，因此该方法一般只能实现特定信号或特定频段的频率识别。

鉴此，提出了基于小波包变换获得时频谱，并通过提取指定频域内时频脊线从而确定结构频率变化时程的方法。相比目前其它时频分析法，该方法更满足时间和频率边缘条件，因此具备更高的准确性。在上述方法的基础上，提出了考虑多维地震作用下，结构地震损伤指标和评估方法。算例结果表明本方法能够较准确地识别结构在不同强度地震下低阶频率的时变过程，从而可对结构整体损伤进行较精确的评估，且该方法机理明确，简单实用。

1基于小波包分解的时变功率谱

结构震害响应蕴含着结构在时域和频域上损伤演变的特性和过程，可利用信号分析技术提取其损伤信息。然而，地震动记录及结构响应信号本身只能在时域上表征损伤信息的非平稳性，通过Fourier变换获得的信号功率谱只能从频域上表征信号的频带能量分布。基于现代信号分析技术的时变功率谱能够从时间、频率和幅值三个方面描述非平稳随机过程的时频局部特性，特别适合在结构动力参数的时变识别中应用。

目前的计算信号时变功率谱的方法主要有短时Fourier变换(Short-time Fourier transform,STFT)、WVD(Wigner-Ville Distribution)分解、S变换、经验模态分解以及小波和小波包变换等[11-14]。由不同信号分析法得到的时变功率谱的数值及表现形式均有所差异，究其原因是目前的各种信号分析法均存在理论或实际运算的不足。WVD分解虽然时频分辨率高，但存在明显的频带交叉项，且其时移不变性和频移不变性特点限制其应用。STFT虽然无交叉项干扰，但时频分辨率低。S变换在高频分辨率上的精度有明显降低。经验模态分解缺乏严密的理论基础和普适性。小波分解在高频段的频率分辨率较差，而在低频段的时间分辨率较差。小波包分解是小波分解的推广，具有更高的时频分辨率和精度。对一个给定的正交小波函数，可以生成一组小波包基。每一个小波包基里提供一种特定的信号分析法，它可以保存信号的能量并根据特征进行精确的重构。在多分辨率分析中，对于给定的基本尺度函数φ(t)和基本小波函数ψ(t)，有双尺度方程

(1)

式中:hk和gk为多分辨分析中定义的一组共轭镜像滤波器。

推广上述双尺度方程，令u0(t)=φ(t)，u1(t)=ψ(t)，定义式(2):

(2)

称{un(t)}为相对于φ(t)的正交小波包。将un(t)进行二进伸缩、平移可得小波包函数

(3)

式中:j为尺度参数，k为平移参数，n为频率参数。

则，信号的小波包分解可表示为

(4)

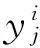
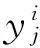
(5)

对不同的窄带信号分别进行时频分析，经整合得到信号整体的时变功率谱或时频谱。由上述分析可知，小波包采用正交小波将信号分解成各尺度上的正交小波包分量，再对各分量用其相应的小波包基函数为窗函数进行时频变换。小波包分解机理明确，由此得到的时变功率谱从理论表达上是准确的，且分辨率高，与前述信号分析技术相比是一种更精细的时频分析法。

需要指出的是，小波包分解中对高频部分进行滤波和抽样时由于不满足Nyquist定理将产生频谱混叠现象，即小波包分解的自然序列与信号频带排列顺序不一致。在时频谱分析中，有必要将小波包分解产生的Paley序子频带按升频序列进行重新排列。此外，选用不同的小波包基函数及分解层数产生的时频谱也有差异，应当通过调试选取正交性、紧支撑性和近似对称性较好的小波包基函数。一般认为，只有离散Meyer(dmey)小波以及ReverseBior小波系和Coiflets小波系中小部分基函数可较准确地描述模拟地震动和结构动力响应的时频变化特征。

2时频谱分析精度评价标准

研究结构动力响应时频功率谱的目的是在坚实数学理论基础上建立合理、可靠、便捷的时频分布，以便准确地同时反映结构动力响应在时间和频率上的能量或强度。根据已有研究成果提出的一系列信号时频分析法可建立不同形式和精度的时频功率谱，采用时域分辨率、频域分辨率、交叉项强弱、抗噪性等定性的指标对由不同分析法获得的时频谱的有效性和准确性进行大致的评判，但如何实现量化评判一直缺乏具体而深入的探讨。

根据Parseval定理可得到非平稳信号y(t)的时间和频率边缘条件如下

(6)

式中：Sy(t,ω)为非平稳信号y(t)的时变功率谱;SFT(t)为信号的Fourier变换幅值谱。式(6)表明：信号某一特定时间的所有频带能量分布之和等于其瞬时能量；信号某一特定频带的能量分布在全部时间上的总和等于能量密度频谱。由精确的时频分析法计算得到的时变功率谱应严格满足上述条件。然而，利用实际的时频分析法得到的时变功率谱很难具有足够的精度，如何量化评价不同方法的准确性虽然重要但相关的研究并不深入。考虑到上述边缘条件，且一般分析中主要注重时变功率谱时频分布特征而通常忽略其幅值的准确性，本文提出利用时域和频域归一化边缘值的误差标准差量化评判时变功率谱的精度(见式(7))。

(7)

式中：Syn(ti,ω)为时变功率谱在时域上边缘值(瞬时能量向量)Sn(ti,ω)的归一化值；yn(ti)为非平稳信号y(ti)的归一化值；Syn(t,ωj)为时变功率谱在频域上边缘值(能量密度频谱向量)Sy(t,ωj)的归一化值；SFn(ωj)为信号Fourier幅值谱的归一化值。

为了比较由不同时频分析法获得的结构动力响应时频谱的精度，选取了某5层钢筋混凝土结构在El Centro(EW)地震波作用下顶层前20 s加速度响应作为分析对象，信号采样频率为50 Hz。值得指出的是，利用HHT或经验模态分解获得的时频谱概念不严密，且其各IMF(Intrinsic Mode Function)分量不正交，频带分布不清晰。虽然近年来有研究者提出通过采用IMF分量正交化技术对HHT时频谱进行修正[15]，但仍不是真正意义上的时变功率谱，不予讨论。此外，基于S变换或Chirplet变换的时频谱不能保证频域上的分辨率，效果不佳，也不予深入研究。上述舍弃的时频方法各具特色，但更适合在某些具体信号的时变特征分析方面应用而不能作为建立准确时变功率谱的通用工具。采用STFT、修正WVD分解、小波分解和小波包分解等获得的最佳时变功率谱(见图1)，其中小波分解所用函数为11层Morlet复小波，小波包基函数为10层离散Meyer小波。对应的频域边缘值和时域边缘值分别见图2和图3。

图1　不同时频分析方法的时变功率谱Fig.1 Power spectra based on different methods

图2　不同时频分析方法的频域边缘值Fig.2 Frequency marginal based on different methods

图3　不同时频分析方法的时域边缘值Fig.3 Time marginal based on different methods

从以上结果可知：结构非线性响应的时变功率谱复杂多变，仅依靠三维谱图表观上无法直接判断其准确度，必须结合时频域边缘值进行量化分析才能比较和评价。由于STFT、修正WVD变换和小波变换不能兼顾时频域的分辨率，因而也不作为获得时变功率谱的可靠工具。以目前的时频分析技术水平，只有利用具有适合的基函数及分解层次的小波包分解才能获得相对精确的时变功率谱。根据式(7)计算得到的时频域边缘数误差的标准差(见图4)，进一步验证了上述结论。由此，后文将只讨论由小波包变换获得的结构地震响应时变功率谱的特征及规律。

图4　时频域边缘数误差的标准差Fig.4 Comparison of SD of the errors in marginal

3基于小波包脊的时变频率提取及结构地震损伤评估

由前文可知，j水平的小波包可通过带通滤波器将结构动力响应信号分解为2j个窄带信号。在时频谱中的各个时间点上作切片并选取能量最大值，即求解时频谱中的频率突变点(局部极值点)便能够获得频率的时变过程，从而可以全面地反映结构损伤的时间、频谱和幅值变化特征。上述方法可视为以时间为走向的时频山脉脊线的提取过程，也可称为小波包脊的提取。结构在地震作用下进入弹塑性状态，不同阶的频率都将有所减小，为了避免频率相互干扰，可针对结构不同阶频率选取相应的频带范围，然后在指定频带的小波包时频谱中提取小波包脊从而识别频率的时变值。

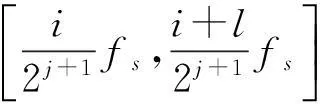
由于频率主要反映了结构整体的动力特性和损伤情况，评估结构在单向水平地震下的损伤时可将结构等效为具有双线形力与变形关系的单自由度体系并研究其频率变化特性(见图5)。设等效体系弹性阶段的刚度为k0，后屈服刚度为αk0；屈服强度和屈服位移分别为fy和uy。若在t时刻结构进入塑性状态且位移达到ue时，等效力为fe(t)，等效刚度为ke(t)，时变延性系数为μe(t)=ue(t)/uy。假定结构的损伤是结构等效刚度损失造成的，则等效线性体系的时变损伤指标D(t)可表示为:

(8)

式中：T0和f0为结构弹性周期和频率;Te(t)和fe(t)

为结构塑性时变等效周期和时变等效频率。利用小波包分解可获得结构某阶时变频率，再根据式(8)便可计算出时变损伤指标，通常可取结构动力时程末段中较稳定的损伤值或整体时程中最大损伤值作为综合等效损伤。根据震后结构的破坏程度和修复水平，可将震害划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌5个等级。参考已有研究成果并结合上述损伤评估方法的特点[16]，定义对应结构不同破坏等级的损伤指标范围(见表1)。通过式(8)和表1便可较便捷地实现结构整体或其在某一方向的损伤评估。

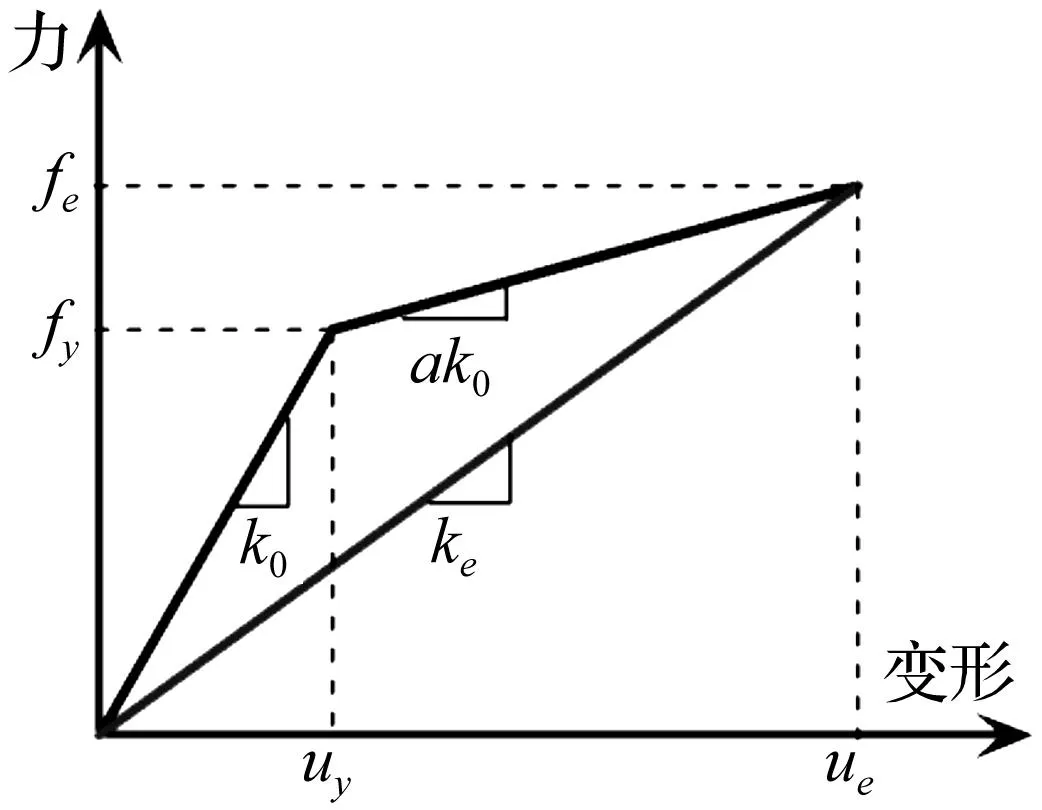
图5　结构单自由度等效体系示意图Fig.5 Scheme of equivalent system with SDOF

损伤程度破坏描述损伤指标基本完好承重构件完好,个别非承重构件轻微损坏,附属构件有不同程度破坏0.00～0.10轻微损伤个别承重构件有轻微残余变形,个别非结构构件明显破坏,附属构件有不同程度破坏0.10～0.20中等破坏多数承重构件有轻微残余变形,部分有明显残余变形,个别非结构构件严重破坏0.20～0.40严重破坏多数承重构件严重破坏或部分倒塌0.40～0.70倒塌多数承重构件倒塌0.70～1.0

然而，式(8)并不能完全反映结构局部损伤状态以及不同方向和振型的综合损伤情况，因此，对于多维复杂结构的时变综合损伤指标Dg可在式(8)的基础上扩展为

(9)

式中:x,y和z为结构三个主轴方向;m,n和p分别为相应方向参与损伤评估的振型数量;ρ为相应的归一化振型参与系数;Dxi为x方向第i个振型对应的损伤指标，γxi为x向振型参与权重，可按下式计算

(10)

这样，根据式(8)～式(10)的计算结果可实现多维复杂结构的综合损伤评估。

4算例

为了验证本文提出的基于小波包脊的时变频率提取及结构地震损伤评估方法的有效性，选取一座5层钢筋混凝土偏心框架结构作为算例，结构所在场地类型为Ⅱ类，抗震设防烈度为8度(见图6)，结构平面尺寸为30 m×6 m，各层层高均为3 m。底部角柱截面600 mm×600 mm，其他柱截面300 mm×300 mm，配筋率为1.2%。梁截面分别为200 mm×500 mm和300 mm×600 mm，配筋率为0.8%。楼板厚120 mm，混凝土强度等级为C35，钢筋采用HRB400。结构在x向和y向的偏心距分别为3 m和0.5 m。结构总质量为5.2×105kg。

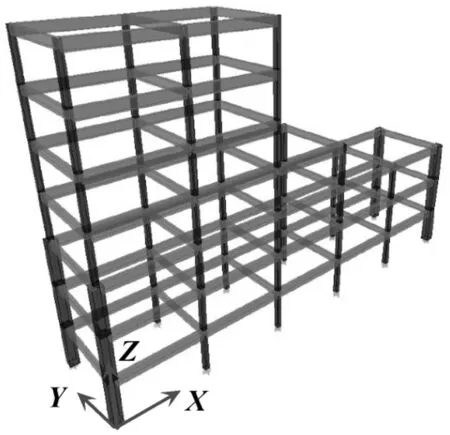
图6　算例结构三维示意图Fig.6 Three-dimensional scheme for example structure

采用非线性有限元软件Opensees建立模型，在El Centro、Taft和Loma Prieta地震记录中分别选用一组典型的三向地震波进行多维弹塑性时程分析。为考虑地震动幅值对损伤程度的影响，依据抗震设计规范要求将每一组地震动X向的加速度幅值分别调至0.11 m/s2、0.22 m/s2和0.51 m/s2，并使X向、Y向和Z向的地震动幅值比例为1∶0.85∶0.65，从而分别作为小震、中震和大震下的地震动输入。

利用Opensees里的时变刚度和频率求解功能提取每一时间子步的各阶频率从而得到时变频率时程，经过适当的多点平滑处理后可作为数值解以备参考。由于结构的顶层响应已经蕴含结构多阶模态信息和结构整体损伤特征，因此选取顶层中间节点的两水平向位移时程分别进行小波包分解，其中小波包基函数为11层离散Meyer小波，从而获得时变功率谱。之后选取适当的频率范围并基于小波包脊提取结构的时变频率，如果频率时程中存在突变点可采用多点平滑算法处理。该结构的前两阶初始弹性周期为1.074 s和0.754 s，分别为X向和Y向第一阶水平振型。振型参与系数分别为0.408和0.329，考虑到竖向振型阶数较高，且相应的损伤较轻，因此可只识别两水平的第一阶频率并用式(8)～式(10)进行单向和综合损伤评估。

图7为El Centro波大震作用下，由顶层中间节点X向水平位移获得的时变功率谱，频率范围为0.55～0.96 Hz。可见小波包脊具有明显的时变特征，表明结构的第一阶频率发生了较大变化，损伤较严重。图8中，图8(a)为由有限元计算得到的时变频率时程和相应的基于小波包脊提取的时变频率，图8(b)为结构位移响应绝对值。两种时变频率均逐渐减少，二者变化趋势一致、终值接近且和响应幅值具有明显的相关性，表明两种方法均能够较真实地反映结构损伤的过程、程度和细节，但后者具有突出的应用性。由于在较严重损伤时结构中较多构件已发生屈服，有限元计算得到的结构时变刚度更多地反映了后屈服刚度特征，因此对应的时变频率一般比真实值偏低，这可通过以上两种方法得到的时变频率存在一定差异提供解释。

图7　结构位移响应时变功率谱Fig.7 Time-frequency power spectrum of response

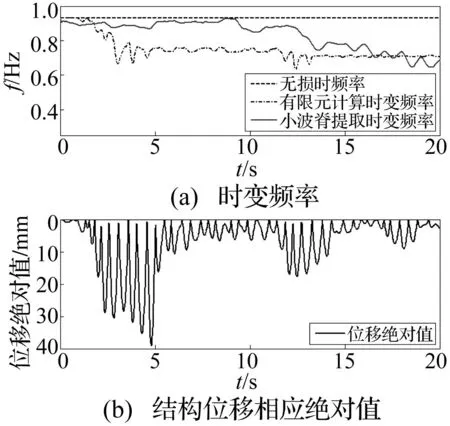
图8　时变频率和位移响应对比Fig.8 Comparison for time-varying frequencies and response

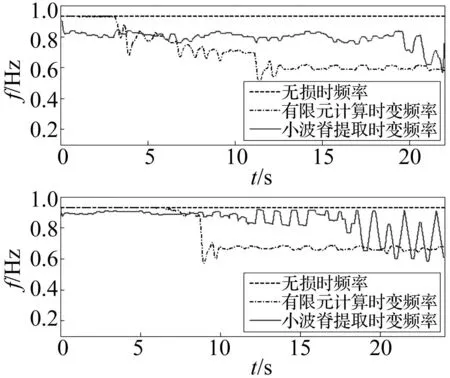
图9　时变频率的对比Fig.9 Instantaneous frequency and time-frequency

图9为X向大震下Taft波和Loma Prieta波作用时结构的时变频率的对比，进一步验证了本文的论述。图10为按式(8)计算得到大震下三组地震的X向损伤指标时程，可见基于时变频率的损伤评估具有良好的通用性和精度。

图11为El Centro波小震和中震下时变频率的对比，结果相对更接近，表明该方法同样适用于中小震害的评估，并具有较高的精度。图12为El Centro大震下按式(8)计算得到的X向和Y向损伤指标时程，以及按式(9)计算得到的结构综合损伤指标时程。参考表1以及有限元分析结果，进一步确定结构发生了严重损伤，验证了本方法的有效性和准确性。

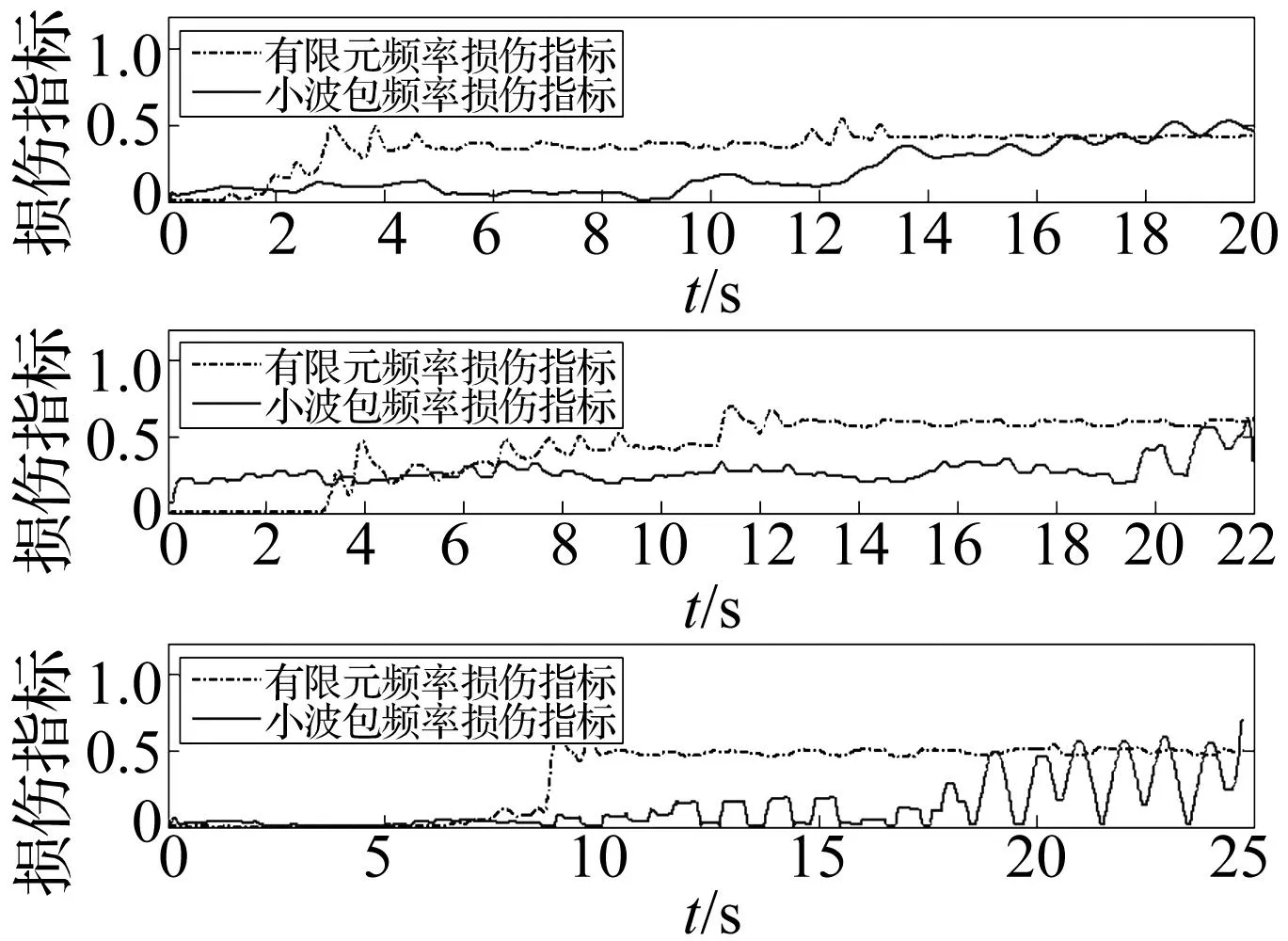
图10　大震下X向损伤指标时程Fig.10 Damage index history in x direction under rare earthquake

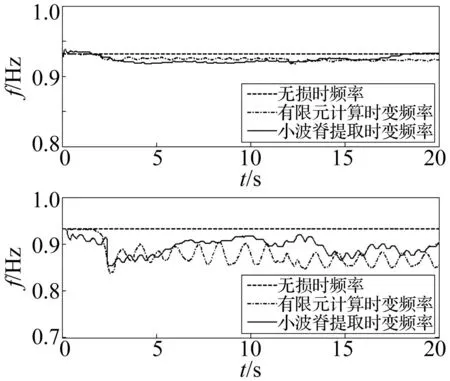
图11　小震和中震下时变频率的对比Fig.11 Instantaneous frequency and time-frequency

确定结构综合等效损伤值可采用损伤指标时程末段中较稳定的数值，表2列出了不同地震及幅值下的综合等效损伤值。可认为该建筑结构在不同地震下均能实现小震下完好，中震下轻微损伤，在大震下发生严重破坏但仍有较强的抗倒塌能力。

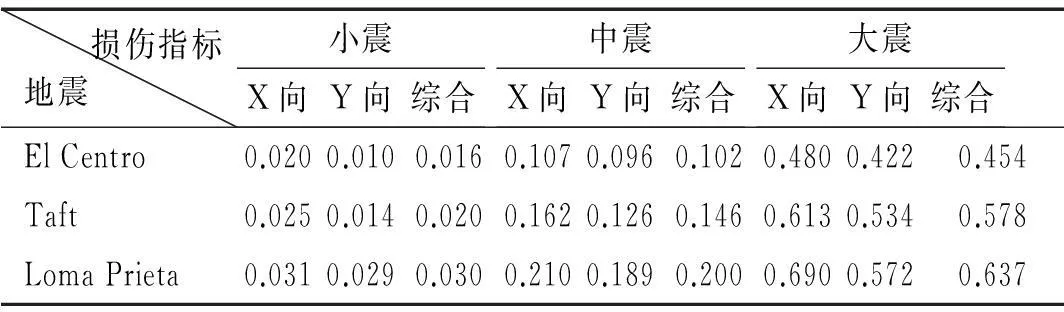
表2　不同震害等级对应的损伤指标范围

图12　各向损伤指标和综合损伤指标Fig.12 Damage index in different directions and overall index

综上所述，本文提出的基于小波包变换和时变频率的结构地震损伤评估法可以较准确地反映结构的整体损伤演变过程和最终损伤程度，可在今后的结构动力分析和验算以及安有地震记录仪和传感器的震后实际结构损伤评估中广泛应用。

5结论

目前大部分工程结构的地震损伤评估方法存在着机理不够明确、指标范围不严格以及性能参数较难实际测试等不足。基于频率或周期变化的损伤评估可以较准确地反映结构整体损伤特性，利用现代时频分析等方法能够获取结构响应的时变功率谱，为研究地震下结构频率时变特性提供了有力工具。但由于地震动和结构响应均是典型的窄带随机过程，频带干扰较严重，传统的时频分析方法较难同时满足时频两域的分辨率要求。本文将满足时间和频率边缘条件的程度作为时频谱分析精度评价标准并从机理上论述了基于特定基函数的小波包变换相对具有更高的时频分辨率和精度。基于小波包变换获得时变功率谱，并通过提取指定频域内时频脊线可较精确地提取结构低阶频率变化的时程。在此基础上，依据结构时变频率的变化可计算出结构的时变损伤程度指标，进而可评估多维地震作用下结构的综合损伤。

算例表明本文提出的基于小波包变换和时变频率的结构地震损伤评估方法，可以较准确地反映结构整体损伤演变过程和最终损伤程度。应用本方法时仅需结构的位移时程，对结构时程分析与验算以及实际结构的震害评估均具有良好的适用性和精度，简单实用。

值得指出的是，小波基函数将显著影响小波包变换的精度，如何针对地震动和结构响应特性选择乃至建立小波基函数需要更深入的探究。目前的小波包变换只能提取差别较明显的低阶频率，如何准确提取高阶频率和密集频率，从而改进基于频率变化评估结构地震损伤方法以使其适合高层复杂结构也需要进一步的研究。

参 考 文 献

[ 1 ] 胡聿贤. 地震工程学[M]. 北京: 地震出版社, 2006.

[ 2 ] 李刚, 程耿东. 基于性能的结构抗震设计-理论、方法与应用[M]. 北京: 科学出版社, 2004.

[ 3 ] He Hao-xiang, Cong Mao-lin. Earthquake damage assessment for RC structures based on fuzzy xets[J].Mathematical Problems in Engineering, 2014, 2013(254865): 1-13.

[ 4 ] Krätzig W B, Petryna Y S. Quasistatic seismic damage indicators for RC structures from dissipating energies in tangential subspaces[J].Mathematical Problems in Engineering, 2014, 2014(615792): 1-11.

[ 5 ] Yang J N, Pan S, Lin S. Least-squares estimation with unknown excitations for damage identification of structures[J].Engineering Mechanics, 2007, 133(1): 12-21.

[ 6 ] Lei Y, Wu Y. Identification of nonlinear structural parameters under limited input and output measurements[J]. International Journal of Non-Linear Mechanics, 2012, 47(4): 1141-1146.

[ 7 ] 伊廷华, 李宏男, 李兵. 地震动信号小波谱分析与结构损伤评估[J]. 振动与冲击, 2006, 25(5): 32-36.

YI Ting-hu，LI Hong-nan，LI Bing. Seismic response analysis using wavelet spectrum and structural damage assessment[J].Journal of Vibration and Shock, 2006, 25(5): 32-36.

[ 8 ] 毛晨曦, 周文松, 欧进萍. 基于小波能量传递函数谱的结构损伤识别[J]. 哈尔滨工程大学学报, 2011, 43(8): 130-134.

MAO Chen-xi，ZHOU Wen-song，OU Jing-ping. Damage assessment based on wavelet energy transfer function spectrum[J].Journal of Harbin Institute of Technology, 2011, 43(8): 130-134.

[ 9 ] Huang N E, Wu Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies[J].Reviews of Geophysics, 2008, 46(1):1-23.

[10] Wang Zuo-cai, Chen Gen-da. A recursive hilbert-huang transform method for time-varying property identification of linear shear-type buildings under base excitations[J]. Journal of Engineering Mechanics, 2012, 138(6): 631-639.

[11] 樊剑, 刘铁, 胡亮. 基于现代时频分析技术的地震波时变谱估计[J]. 振动与冲击, 2007, 26(11): 79-82.

FAN Jian，LIU Tie，HU Liang. Time-varying spectrum estimation of earthquake ground motion via modern time-frequency analysis[J].Journal of Vibration and Shock, 2007, 26(11): 79-82.

[12] Priestley M B. Power spectral analysis of nonstationary random processes[J].Journal of Sound and Vibration, 1967, 6(1): 86-97.

[13] Cohen L. Time-Frequency Analysis: theory and Applications [M]. New York, Prentice-Hall, 1995.

[14] 张贤达, 保铮. 非平稳信号分析与处理[M] .北京:国防工业出版社，1998.

[15] 陈清军, 李英成. 基于演变谱和正交化HHT法的类谐和长周期地震动合成[J]. 湖南大学学报, 2012, 39(11): 20-27.

CHEN Qing-jun，LI Ying-cheng. Simulation of harmonic-like long-period ground motion based on evolutionary spectra and orthogonal HHT method[J].Journal of Hunan University, 2012, 39(11): 20-27.

[16] 李宏男. 结构多维抗震理论[M]. 北京:科学出版社, 2006.

Structural seismic damage assessment based on wavelet packet transformation and time-varying frequencies

HEHao-xiang1,2,CHENKui1,YANWei-ming1,2(1．Beijing Municipal Key Lab of Earthquake Engineering and Structural Retrofit，Beijing University of Technology, Beijing 100124，China; 2．Beijing Collaborative Innovation Center for Metropolitan Transportation, Beijing 100124，China)

Abstract:The structural seismic damage assessment method based on frequency changes has the advantages, such as, clear mechanism and high precision, but the time-frequency resolution for the traditional methods of signal analysis can not accurately meet the requirements of precision. Hence, the time-varying frequencies cannot be obtained directly from the response signals and the application of this damage assessment method is affected. Here, accuracy evaluation criteria for different signal analysis methods were presented based on marginal conditions in time-frequency domain, and the wavelet packet decomposition method with special wavelet basis functions was verified as an efficient tool to establish time-varying power spectrum on the basis of theoretical and computational analyses. The time-varying frequency extraction method based on wavelet packet ridge was proposed, and the structural time-varying seismic damage index was calculated according to structural frequency changes, furthermore, the structural multi-dimensional seismic damage assessment was realized. The examples showed that the seismic damage assessment method based on wavelet packet transformation and time-varying frequencies can accurately reveal the overall damage evolution process and the eventual damage level of a structure; this method only requires structural displacement histories, and has a good applicability for structural dynamic analysis, seismic design verification and seismic damage assessment of actual structures.

Key words:earthquake; damage assessment; wavelet packet transformation; time-varying frequency; time-varying power spectrum

中图分类号:TU362; TN911. 6

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.004

收稿日期：2015-01-13修改稿收到日期：2015-04-19

基金项目：国家自然科学基金项目(51478024); 工程抗震与结构诊治北京市重点实验室重点项目(USDE201403)

第一作者 何浩祥 男，博士，副研究员，1978年生

E-mail: hhx7856@163.com