超越离合-单对齿轮副系统的建模及非线性特性研究

王　鹏, 李平康, 贾智州(北京交通大学 机械与电子控制工程学院，北京　100044)



超越离合-单对齿轮副系统的建模及非线性特性研究

王鹏, 李平康, 贾智州(北京交通大学 机械与电子控制工程学院，北京100044)

摘要：建立了考虑间隙、时变啮合刚度、综合传动误差的超越离合-单对齿轮副系统的非线性动力学模型，并给出评价该系统分岔、振动、载荷以及碰撞特性的综合性能指标。通过对系统分岔与混沌特性的研究，揭示了该系统响应随着激励频率变化时所经历的倍周期分岔、准周期分岔、阵发分岔等几类通向混沌分岔路径共存的复杂分岔路径，体现了超越离合-单对齿轮副系统非线性动力学行为的复杂性态；通过对参数影响趋势的研究，总结了有关超越离合-单对齿轮副系统的一般性动态设计准则。

关键词：间隙；超越离合-单对齿轮副系统；混沌；动态设计准则

机械系统的碰撞振动所引起的噪声会对人们的生活、生产环境造成负面影响。但由于生产过程中工艺水平的限制，加之机械装配过程中需考虑零件的热胀冷缩，机械部件之间不可避免地存在间隙。这些间隙的存在必然导致机械装置在运行中发生碰撞振动，如齿轮拍击(rattling)[1]、引擎的锤击(hammering)[2]等。零部件间的碰撞振动可能改变机构动力系统运动的拓扑结构，给机构的动态设计带来了相当大的难度, 也是造成机械部件损坏的主要原因之一[3]。

在稳态工况条件下，车辆自动变速器可简化为由齿轮与超越离合器所组成的“可控超越离合集成系统”，其最基本形式就是由单对齿轮副与超越离合器串联而成的“超越离合-单对齿轮副系统”，如图1所示。从动力学的角度分析，该系统是一个由齿轮与超越离合器这两类分段光滑系统耦合而成的，包含着间隙这一强非线性因素的复合动力系统。该系统比单纯的齿轮或离合器系统更加复杂，多重强非线性因素的存在也将对系统响应形式造成潜在的复杂影响。对该系统非线性动力学特性的研究，可为解释此类系统中产生的非线性行为提供依据，得到关于该系统的一般性动态设计准则；同时，也为探讨结构更加复杂的可控超越离合集成系统非线性动力学问题奠定基础。迄今，相关文献[4]虽涉及到这方面的内容，但该系统在间隙等强非线性因素激励下的混沌特性与分岔路径的讨论尚不多见。

基于上述原因，本文将建立考虑间隙、时变啮合刚度与综合传递误差等非线性因素的超越离合-单对齿轮副系统动力学模型，采用数值积分法对该系统随激振频率变化的分岔结构及通向混沌的途径，及参数影响规律进行了讨论。

图1　超越离合-单对齿轮副系统结构简图Fig.1 Structure of the overrunning-clutch-single pair gear system

1超越离合-单对齿轮副系统建模

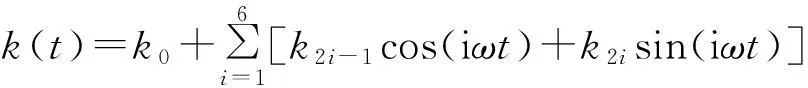
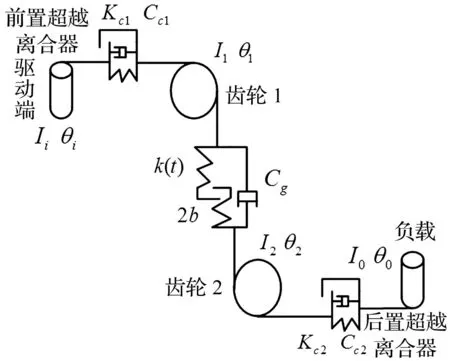
图2　超越离合-单对齿轮副系统模型简图Fig.2 Model of the overrunning clutch-single pair gear system

根据牛顿第二定律，分别以前置超越离合器、主动齿轮、被动齿轮、后置超越离合器为研究对象，可推得系统运动微分方程如下：

(1)

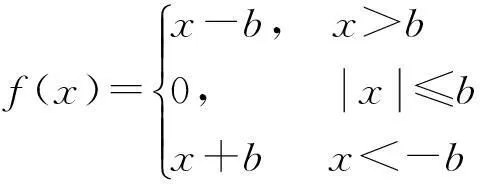
根据牛顿第二定律，参考文献[4]，建立超越离合器模型如下：

(2)

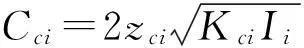
定义齿轮1、齿轮2与前、后置超越离合器在啮合线上的位移为x1、x2、xi、xo，则有：

x1=Rb1θ1，x2=Rb2θ2，xi=Rb1θi，xo=Rb2θo

相应地，式(1)转化为如下形式：

(3)

式中：m1、m2、mi、mo表示齿轮1、齿轮2与前、后置超越离合器在齿轮副啮合线上的当量质量，即m=I/Rb2；FD=TD/Rb1表示等效到齿轮1基圆上的前置超越离合器的驱动力；FL=TL/Rb2表示等效到齿轮2基圆上的后置超越离合器的阻力；Fc1=Tc1/Rb1表示等效到齿轮1基圆上的前置超越离合器作用力；Fc2=Tc2/Rb2表示等效到齿轮2基圆上的后置超越离合器作用力；c=Cg。

引入齿轮副传动误差q，设：

(4)

式中：qi和qo表示前置超越离合器与齿轮1，以及齿轮2与后置超越离合器的相对位移。

根据式(4)的关系，将式(3)进行代数变换，可得：

(5)

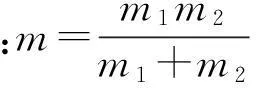
定义无量纲时间尺度τ=tωn与位移尺度bc，令：

(6)

将式(6)代入式(5)可得：

(7)

式中：

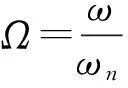
式(2)超越离合器模型转化为如下形式：

(8)

将式(8)代入式(7)，可得超越离合-单对齿轮副系统无量纲化模型如下：

(9)

2评价系统的综合性能指标

为考察参数对可控超越离合集成系统综合传动性能的影响，首先要明确评价该类系统综合性能的指标，进而才能通过仿真研究得到比较全面的一般性动态设计准则。在本文研究中，拟从分岔特性、振动特性、载荷特性以及碰撞特性等4个方面对该系统传动性能进行评价与对比。具体而言：以“分岔图[5]”反映系统的分岔特性，描述系统响应形式随参数的变化规律；以“动态传递误差(Dynamic Transmission Error，DTE)”及其“振动成分(Oscillating DTE，ODTE)”指标反映系统的振动特性[4]，DTE和ODTE分别描述齿轮副的传递误差的大小以及齿轮系统中噪声与振动的强弱程度；以“动载荷系数[6]”反映系统的载荷特性，描述系统内部产生的动载荷的强弱程度；以“冲击状态[7]”描述系统的碰撞特性，描述系统在运行过程中是否产生冲击现象及冲击的类型。

3系统的分岔与混沌特性

采用变步长Gill算法对超越离合器-单对齿轮副系统进行求解，该系统主要名义参数包括：主动齿轮齿数z1=23，被动齿轮齿数z2=121，模数M=2.5 mm，齿宽B=14 mm，压力角α=20°，重合度ε=1.477，大小齿轮均未变位。齿轮啮合阻尼比ζ=0.02，离合器阻尼比zc1=zc2=0.01，主动齿轮转动惯量I1=6.901 3×10-5kg·m2，被动齿轮转动惯量I2=5.286 4×10-2kg·m2，前置超越离合器转动惯量Ii=I1，后置超越离合器转动惯量Io=I2，主动齿轮基圆半径Rb1=21.6 mm，被动齿轮基圆半径Rb2=113.7 mm，齿轮副平均啮合刚度k0=1.283 7×109N/m，传动误差幅值ea=2×10-7m，齿侧间隙b=1×10-6m，长度尺度bc=1×10-6m，等效到啮合线上的驱动力与阻力FD=FL=128.37 N，超越离合器扭转刚度Kc=1.5×104Nm/rad。

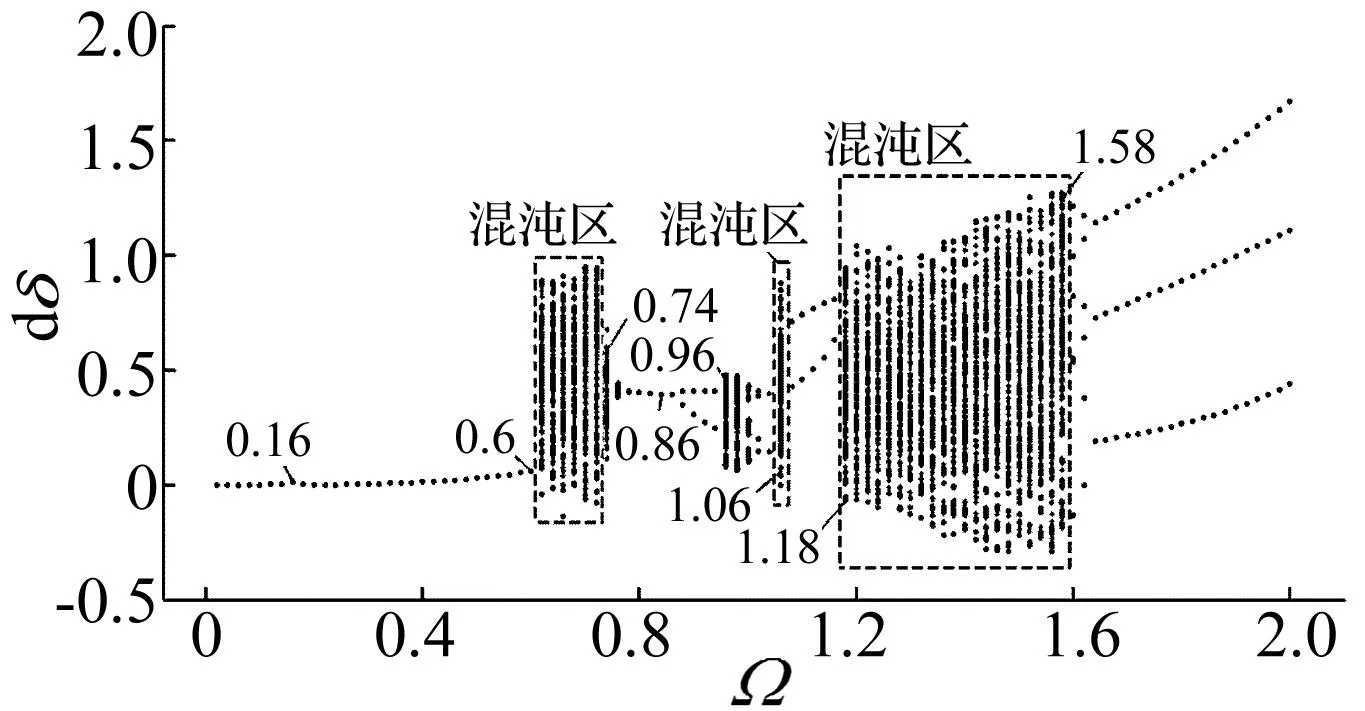
图3　超越离合-单对齿轮副系统的全局分岔图Fig.3 Global bifurcation diagram of OC-SGPS

图3为超越离合-单对齿轮副系统随激振频率Ω变化时的全局分岔图。系统在整个频域上的主要演变频点所对应的时域图与Poincaré映射如图4所示。系统响应形式的演变过程为：当Ω≤0.6时，系统为单周期响应(图4(a))，在Ω=0.16处附近均得到了次谐波共振；在Ω=0.62处，系统的响应形式发生了由规则响应向复杂周期响应的突变，即“阵发分岔”行为，单周期响应经由阵发分岔进入混沌响应区(图4(b))；经历Ω=0.62～0.72的混沌响应区后，在Ω=0.74处，系统的响应形式经由拟周期响应逐渐过渡为周期响应，系统发生“拟周期分岔”并归于单周期响应(图4(c))；在Ω=0.86处发生了1T-2T的“倍周期分岔”，形成周期2解(图5(d))；在Ω=0.96处，再次经历“阵发分岔”进入一个2T-1T的逆“倍周期分岔”归为2周期解，在Ω=1.06处出现了一个狭窄的混沌响应区(图4(e))，随后突变为周期2响应(图4(f))；最后在经历了Ω=1.18～1.58的混沌响应区后(图4(g))，经由逆“倍周期分岔”过程，归为周期3响应(图4(h))。

(a)Ω=0.5(b)Ω=0.68

(c)Ω=0.82(d)Ω=0.92

(e)Ω=1.06(f)Ω=1.12

(g)Ω=1.4(h)Ω=1.8

(i)Ω=0.75(j)Ω=0.993图4 关键演化频点的时域图与Poincaré映射图Fig.4TimedomainchartandPoincarémapofthekeyevolutionalfrequencypoints

为体现上述分岔过程中倍周期分岔、准周期分岔、阵发分岔的局部结构，在Ω=0.74、0.96、1.18、1.58频点附近对分岔图进行细化。由图5(a)，在Ω=0.74附近频段上出现了“拟周期分岔”，系统由单周期响应过渡到混沌响应的过程中经历了拟周期响应(图4(i))。由图5(c)，在Ω=1.18附近频段上出现了“阵发分岔”，系统不经历拟周期响应形式直接由周期2响应突变为混沌响应。由图5(d)，在Ω=1.58附近频段上出现了逆“倍周期分岔”现象，系统随激振频率逆向由3T-6T-12T…逐渐过渡到混沌响应。由图5(b)，在Ω=0.96附近频段上出现了一个较复杂的局部分岔区，系统经历了正、逆“倍周期分岔”的更替，且在正、逆“倍周期分岔”之间隐含着一个混沌响应区(图4(j))，并最终仍归于周期2响应。

(a)Ω=0.74附近(b)Ω=0.96附近(c)Ω=1.18附近(d)Ω=1.58附近图5 超越离合-单对齿轮副系统的局部分岔图Fig.5LocalbifurcationdiagramofofOC-SGPS

4参数对系统综合性能的影响

在以下对参数影响规律的讨论中，均以名义参数为基准值，参数名加后缀“_nomi”表示某参量的名义值，例如Kc1_nomi表示前置超越离合器刚度的名义值。

4.1前置超越离合器刚度的影响

当超越离合器刚度在0.1倍～10倍名义刚度值范围内变化时，基本覆盖了超越离合器常用材料刚度的选取区间。

如图6所示，当Kc1在0.1Kc1_nomi～10Kc1_nomi的范围内变化时，系统的分岔结构、混沌响应的分布区域均发生了显著的变化；并且，在较高频段上，混沌响应的范围随Kc1的增大而逐渐变宽，反映出Kc1的增大具有使较高频段上的响应形式复杂化的趋势。由图7所示的系统振动、载荷、碰撞性能指标看，各指标均发生了复杂的变化；唯一不变的是后置超越离合器的碰撞性能指标，始终处于“无冲击状态”(取值为“0”，表示“无冲击状态”)，可见Kc1对后置超越离合器碰撞特性影响较弱。

(a) 0.1Kc1_nomi(b) Kc1_nomi(c) 5Kc1_nomi(d) 10Kc1_nomi图6 Kc1对系统分岔特性的影响Fig.6TheimpactofKc1onbifurcationfeatureofOC-SGPS

当系统中各环节阻尼比较低时，间隙等非线性因素的存在使得系统其振动、载荷、碰撞指标在频域上的表现十分复杂，难以对Kc1的影响趋势进行有效的评估。为此，采取“适度增大系统阻尼比”的方法，削弱非线性因素的影响，使系统响应形式趋于规则化，进而更显著地体现Kc1对系统性能指标的影响趋势。为此，将齿轮副啮合阻尼比z、前置离合器阻尼比zc1、后置离合器阻尼比zc2同时增大10倍，增大系统阻尼比后的综合性能指标如图8、图9所示。

如图8所示，在增加系统的阻尼比后，混沌以及准周期等复杂周期的响应形式得到了有效的抑制，只有当前置超越离合器刚度取10Kc1_nomi时，在Ω=1.4附近的邻域上尚存有小范围的准周期响应区，这也表明较高的前置超越离合器刚度容易诱发长周期响应的产生。如图9(b)所示，随着Kc1的增大，前置超越离合器的动载荷系数均值随之增大；但是齿轮副与后置超越离合器动载荷系数均值几乎没有发生变化。如图9(c)所示，随着Kc1的增加，前置超越离合器发生冲击的频段有加宽的趋势；而齿轮副发生单边冲击的频段基本对应于齿轮副ODTE指标大于1×10-3的频段。

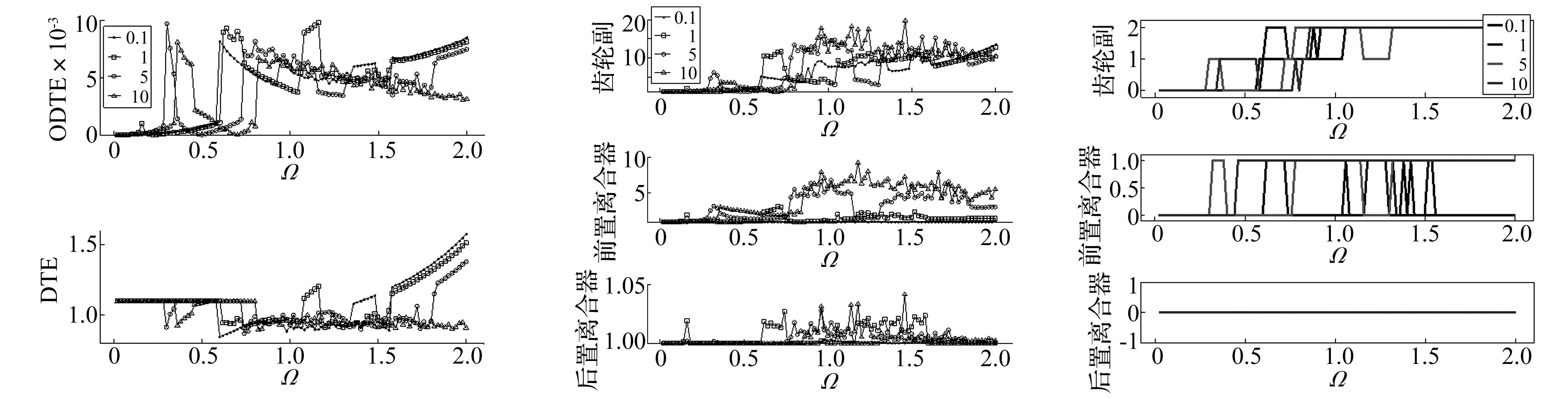
(a)　振动特性　　　　　　　　　　　(b)　 载荷特性　　　　　　　　　　　(c)　碰撞特性图7　Kc1对系统综合性能指标的影响Fig.7 The impact of Kc1 on indexes of OC-SGPS

(a)　0.1Kc1_nomi　　　　　　　　(b)　Kc1_nomi　　　　　　　　(c)　5Kc1_nomi　　　　　　　　(d)　10Kc1_nomi图8　Kc1对系统综合性能指标的影响(增大阻尼比)Fig.8 The impact of Kc1 on indexes of OC-SGPS(Damping ratio heightened)

(a)　振动特性　　　　　　　　　　　(b)　载荷特性　　　　　　　　　　　(c)　碰撞特性图9　Kc1对系统综合性能指标的影响(增大阻尼比)Fig.9 The impact of Kc1 on indexes of OC-SGPS(Damping ratio heightened)

4.2后置超越离合器刚度的影响

通过对后置超越离合器刚度Kc2影响趋势的研究获知：后置超越离合器刚度Kc2只对后置超越离合器动载荷系数产生影响，该指标随Kc2的增大而增大，但增幅有限；而对其余各指标几乎没有发生任何影响。本文仅给出如图10所示的增大z、zc1、zc2后系统动载荷系数的对比结果。

图10　Kc2对系统综合性能指标的影响(增大阻尼比)Fig.10 The impact of Kc2 on indexes of OC-SGPS(Damping ratio heightened)

4.3前置超越离合器阻尼比的影响

考察超越离合器阻尼比在1倍～50倍阻尼比名义值范围内变化时，对系统综合性能指标的影响。超越离合器阻尼比的名义值为0.02，对应的阻尼比将在0.02～1.0之间变化，覆盖了阻尼比可能的变化范围。

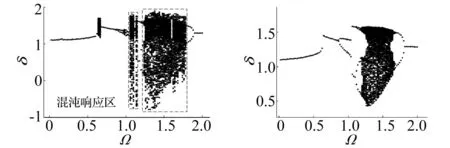
(a)　10zc1_nomi 　　　　　　(b)　50zc1_nomi图11　zc1对系统分岔特性的影响Fig.11 The impact of zc1 on bifurcation feature of OC-SGPS

如图11所示，当前置超越离合器阻尼比zc1在z1_nomi～50zc1_nomi的范围内增大时，虽然系统分岔结构发生了变化，在Ω=1～2频域内系统的响应形式由“混沌响应”(图12(a)、图12(b))转变为“准周期响应”(图12(c))，但并没有抑制复杂周期响应形式的出现。由图13(a)、图13(b)所示，zc1的增大可以有效地抑制发

生在Ω=0.16处的次谐波共振，以及振动与载荷特性指标在混沌响应区上的波动，减小软弹簧特性跳跃的幅度，降低各组件动载荷系数的均值，但却无法避免跳

跃现象的发生。对比图14所示，齿轮副阻尼比z对系统载荷特性的影响趋势看，当z增大时，不仅载荷特性指标在混沌响应区上的波动被抑制，且当z增大到一定数值时，系统的软弹簧特性以及跳跃现象基本上被完全消除，但未能对次谐波共振形成干预。从这个角度看，zc1与z，即前置离合器与齿轮副啮合阻尼比刚好形成互补，适当的选取两个阻尼比值可以同时对系统的软弹簧特性、跳跃以及次谐波共振进行有效的抑制。

如图13(c)所示，随着zc1的增大，齿轮副的双边碰撞行为以及前置超越离合器的碰撞行为逐渐被抑制，唯有后置超越离合器始终保持为楔合状态，未发生冲击。总体上看，系统碰撞特性随zc1的增大而有所改善。

4.4后置超越离合器阻尼比的影响

通过对后置超越离合器阻尼比zc2影响趋势的研究发现：后置超越离合器刚度zc2只对后置超越离合器动载荷系数产生影响，该指标随zc2的增大而减小，但减幅有限；而对其余各指标几乎没有发生影响。本文仅给出如图15所示的系统动载荷系数对比结果。

总结本文关于参数对超越离合-单齿轮副系统各性能指标影响趋势的研究结果，将主要结论归纳如下，如表1所示。

(a) Ω=1.08(10zc1_nomi)(b)Ω=1.50(10zc1_nomi)(c)Ω=1.50(50zc1_nomi)图12 zc1变化时关键频点上的Poincaré映射Fig.12Poincarémappingonkeyfrequencypointswithzc1changed

(a)　振动特性 (b)　载荷特性 (c)　碰撞特性图13　zc1对系统综合性能指标的影响Fig.13 The impact of zc1 on indexes of OC-SGPS

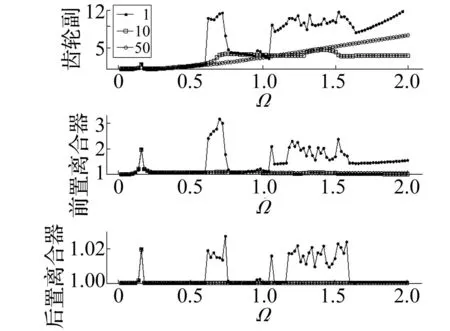
图14　z对系统载荷特性的影响Fig.14 The impact of z on load feature of OC-SGPS

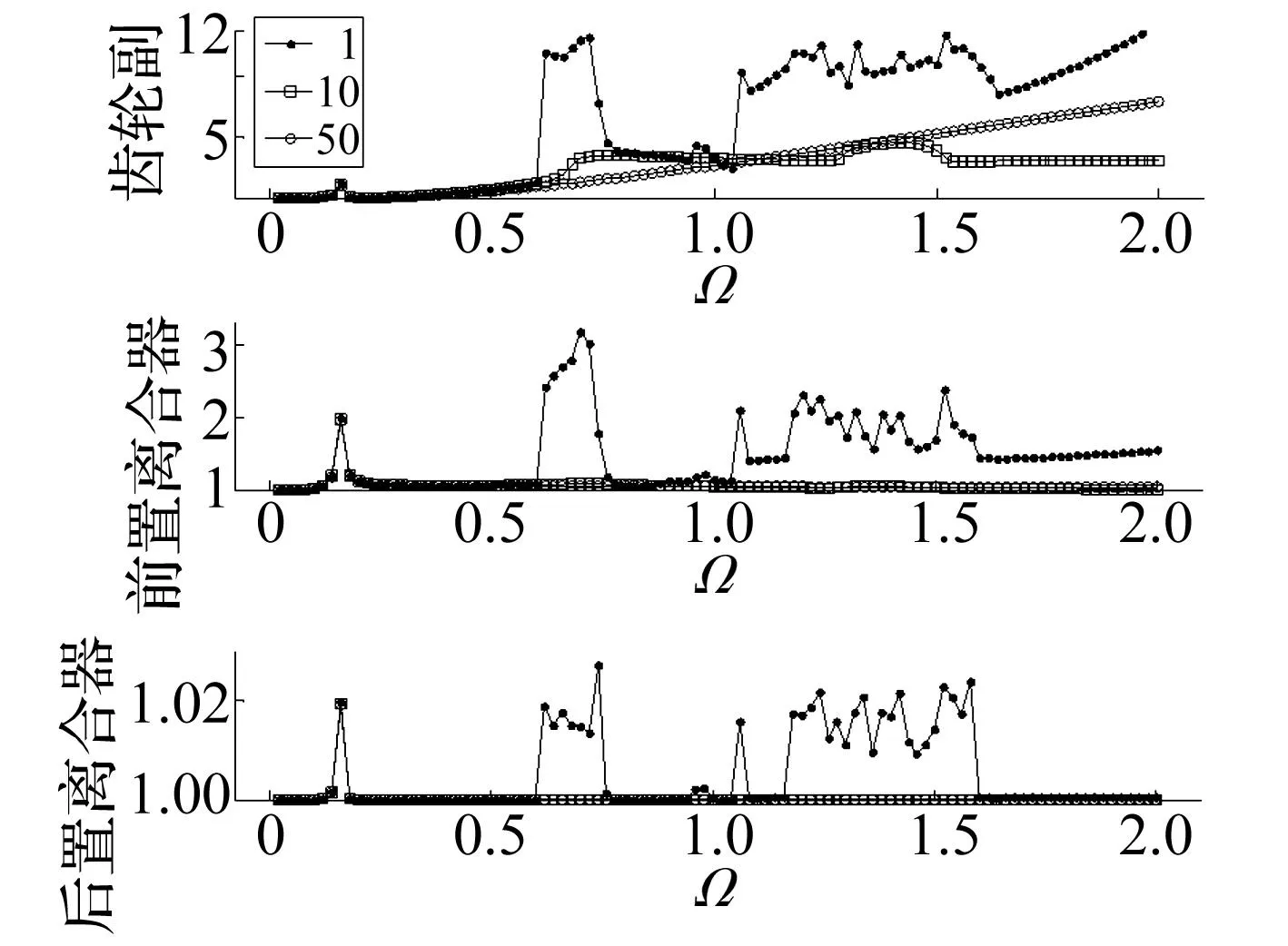
图15　zc2对系统载荷特性的影响Fig.15 The impact of zc2 on load feature of OC-SGPS

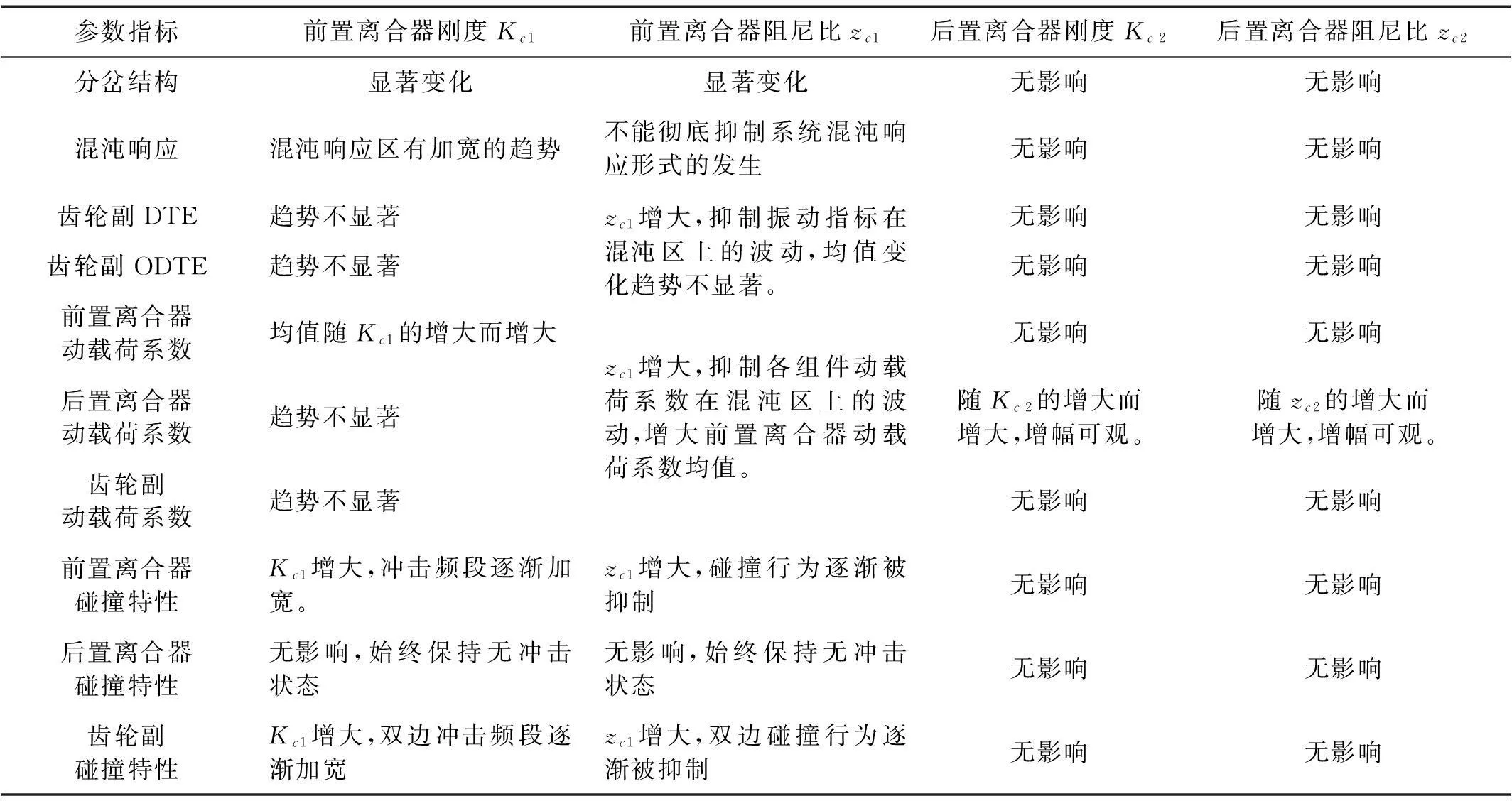
参数指标前置离合器刚度Kc1前置离合器阻尼比zc1后置离合器刚度Kc2后置离合器阻尼比zc2分岔结构显著变化显著变化无影响无影响混沌响应混沌响应区有加宽的趋势不能彻底抑制系统混沌响应形式的发生无影响无影响齿轮副DTE趋势不显著zc1增大,抑制振动指标在混沌区上的波动,均值变化趋势不显著。无影响无影响齿轮副ODTE趋势不显著无影响无影响前置离合器动载荷系数均值随Kc1的增大而增大无影响无影响后置离合器动载荷系数趋势不显著zc1增大,抑制各组件动载荷系数在混沌区上的波动,增大前置离合器动载荷系数均值。随Kc2的增大而增大,增幅可观。随zc2的增大而增大,增幅可观。齿轮副动载荷系数趋势不显著无影响无影响前置离合器碰撞特性Kc1增大,冲击频段逐渐加宽。zc1增大,碰撞行为逐渐被抑制无影响无影响后置离合器碰撞特性无影响,始终保持无冲击状态无影响,始终保持无冲击状态无影响无影响齿轮副碰撞特性Kc1增大,双边冲击频段逐渐加宽zc1增大,双边碰撞行为逐渐被抑制无影响无影响

5结论

本文给出了评价超越离合-单对齿轮副系统分岔、振动、载荷以及碰撞特性的综合性能指标；通过对系统分岔与混沌特性的研究，揭示了此类系统响应随着激励频率变化时所经历的，倍周期分岔、准周期分岔、阵发分岔等几类通向混沌分岔路径共存的复杂分岔路径，体现了超越离合-单对齿轮副系统非线性动力学行为的复杂性态；通过对参数影响趋势的研究，系统地总结了超越离合-单对齿轮副系统的一般性动态设计准则，也为合理解释此类传动系中一些故障的产生原因提供理论依据。

参 考 文 献

[1] Feng Q, Pfeiffer F. Stochastic model on a rattling system[J].Journal of Sound and Vibration, 1998, 215(3):439-453.

[2] Pfeiffer F, Prestl W. Hammering in diesel-engine driveline systems[J].Nonlinear Dynamics, 1994, 5(4):477-492.

[3] Ko P L. Wear of power plant components due to impact and sliding[J].Applied Mechanics Reviews,1997,50(7):387-411.

[4] Cheon G J. Withdrawn: nonlinear behavior analysis of spur gear pairs with a one-way clutch[J].Journal of Sound and Vibration, 2007, 304(1):18-30.

[5] Al-Shyyab A, Kahraman A. Anon-linear dynamic model for planetary gear sets[J].Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2007, 221(4):567-576.

[6] 孙智民, 沈允文, 李素友. 封闭行星齿轮传动系统的动态特性研究[J].机械工程学报, 2002, 38(2):44-48.

SUN Zhi-min, SHEN Yun-wen, LI Su-you. Study on dynamic behavior of enchased differential gear train[J].Chinese Journal of Mechanical Engineering, 2002, 38(2):44-48.

[7] 孙涛. 行星齿轮系统非线性动力学研究[D].西安: 西北工业大学, 2000.

Model and nonlinear characteristic analysis of the overrunning clutch-single pair gear system

WANGPeng,LIPing-kang,JIAZhi-zhou(School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract:By taking clearance, time-varying meshing stiffness and transmission error into account, a nonlinear dynamic model of the overrunning clutch-single pair gear system (OC-SPGS) has been established.Comprehensive performance indices about the performance of the bifurcation, vibration, load and contact have been given.Research on bifurcation and chaotic features reveals complex bifurcation roads with excitation frequency changes, which comprise the period-doubling bifurcation, quasi-periodic bifurcation and intermittency bifurcation.Additionally, general dynamic design criteria for OC-SPGS have been summarized based on research on the parameters’ influence.

Key words:clearance; overrunning clutch-single pair gear system(OC-SPGS); chaos; dynamic design criteria

中图分类号:U463.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.037

通信作者李平康 男，教授，博士生导师，1955年生

收稿日期：2014-12-24修改稿收到日期：2015-04-07

基金项目：国家自然科学基金项目(61074104)

第一作者 王鹏 男，博士生，1981年2月生

E-mail：pkli@bjtu.edu.cn