基于伪随机特征向量的二次修改的结构拓扑重分析

何建军, 陈享姿(长沙理工大学 汽车与机械工程学院，长沙　410114)



基于伪随机特征向量的二次修改的结构拓扑重分析

何建军, 陈享姿(长沙理工大学 汽车与机械工程学院，长沙410114)

摘要：研究了连续两次修改的结构动力学拓扑重分析问题。基于我们提出的特征向量伪随机初始化方法，独立和耦合质量正交化处理措施，再结合瑞利-里兹分析法，形成了适用于两次修改的增加自由度的结构拓扑大修改的快速动力学重分析方法。该方法减少了两次直接分析所需要的大量计算量，且操作简单，易于实现。数值算例结果表明，对于这类涉及两次修改的拓扑大修改重分析问题，该方法是十分有效和高精度的。

关键词：连续两次修改；伪随机；动力学拓扑重分析；质量正交化

优化设计往往是一个不断重复的迭代过程。有理论分析表明，大型复杂结构拓扑构型可能有无穷多，这导致结构拓扑优化设计迭代次数多，计算时间长，严重影响了结构拓扑优化设计的效率和其在工程实际中的实用性[1]。其中，重复的结构直接分析计算又占据了结构优化设计中主要的计算量和时间，而相比直接分析，结构近似重分析却能够有效的减少结构优化设计中的计算量，显著的加快拓扑优化设计的进度，从而有利于结构拓扑优化设计在工程实际中的广泛应用和普及，因此开展结构拓扑优化设计重分析方法的研究仍然是一项很有意义的工作。

目前，结构重分析方法的研究拓展到了区间参数结构修改的特征值重分析[2]，规则结构局部修改的特征值重分析[3]，复特征值的近似重分析[4]和线性结构随机分析的重分析方法[5]等一些新的重分析问题[6-7]上来，这些都表明结构重分析方法的研究仍然是结构优化设计中一项很值得关注的重要内容。

现有的结构近似重分析方法对于一次拓扑修改，可能具有良好的精度，那么对于两次(这里的两次是指第一次修改重分析以初始结构的特征信息为基础，而第二次修改后的新结构重分析又以第一次近似重分析的结果为基础)或者多次修改却难以继续保持好的近似性。假设对于第二次修改，采用第一次修改近似重分析的结果作基础获得的再次重分析结果不理想，设计者又不得不反过来再对第一次修改后的新结构进行完整或直接的重分析，这样近似重分析方法减少的计算时间就比较有限，其实际实用就会受到限制。因此，本文基于我们提出的独立和耦合质量正交化处理措施和特征向量伪随机初始化方法，再结合瑞利-里兹分析法，对一类新的涉及连续两次修改的拓扑大修改重分析问题进行了研究，数值算例结果表明了方法的有效性。

1动力学方程

假设拓扑修改前初始结构的自由度为m，其广义特征方程为

(1)

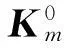
同理，再令增加了n自由度的拓扑优化后新结构的特征值问题表述如下

Km+nΨi=λiMm+nΨi

(2)

式中，Km+n和Mm+n分别表示拓扑修改后结构的刚度矩阵和质量矩阵；而λi和Ψi分别表示其第i阶特征值及相应的特征向量,m+n表示拓扑优化结构的有限元离散自由度数。

显然，依据初始结构和新增加结构之间的连接关系，对矩阵分块，式(2)中拓扑优化结构的Km+n、Mm+n可写成

(3)

(4)

也可以将上式表示为更简洁的形式

(5)

以上及接下来的表达式中，下标“m”表示初始结构的自由度数，而“n”表示新增加的自由度数。

于是，动力学拓扑重分析构造的问题就是在不直接求解式(2)和节省计算量的前提下，通过间接的方法获得拓扑修改结构的近似特征值及特征向量。

2连续两次修改的结构动力学拓扑大修改重分析方法

2.1新增加自由度上特征向量的初始化

对于自由度增加的结构拓扑修改，可先将拓扑优化后新结构的自由度分为独立的两部分，其对应的特征向量也分为两部分

Ψi=[(Ψmi)Τ(Ψni)Τ]，(i≪m)

(6)

式中，Ψmi和Ψni分别对应初始结构自由度和新增加自由度上的特征向量。

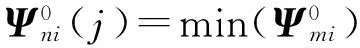
(7)

2.2独立质量正交化处理

现有的重分析方法都忽略了初始自由度和新增加自由度之间的独立关系，因此为了突出两者的独立性质和效果，我们提出了独立质量正交化处理的新策略，简称解耦质量正交化处理。数值计算结果表明，这一策略对于改善近似拓扑重分析方法的精度具有非常显著的作用。

初始自由度：

(8)

新增加自由度：

ΚnnΨni=ΜnnΨni

(9)

2.3整个自由度上的瑞利-里兹分析

本质上，单元由于彼此之间的连接关系组成了一个整体-结构，结构初始自由度和新增加自由度上特征向量的耦合作用才是决定整个模态特征的主要因素，因此，为了获得整个自由度上特征向量的优良近似结果，再对整个自由度上的特征向量进行质量正交化处理和瑞利-里兹分析。

(1) 通过质量正交化处理改善由式(8)，(9)得到的拓扑修改结构整个离散自由度上的初始特征向量

Κm+nΨi=Μm+n[(Ψmi)T(Ψni)T]T

(10)

(2) 基于式(10)得到的近似基向量，计算投影子空间

Κr=(Ψr)TKm+n)Ψi

(11)

Mr=(Ψr)TMm+n)Ψi

(12)

(3) 进行瑞利-里兹分析

ΚrΨri=λriMm+n)Ψi

(13)

(4) 通过上述一系列的改善策略和里兹分析过程，最终由下式可得到拓扑修改结构的高精度的近似特征值和特征向量

λi=λri, Ψ=[(Ψm)T(Ψn)T]T[Ψr]

(14)

从该方法的整个流程可以看出，所有环节简单、易懂和通用，而且其中包含一些相似的分析部分，因此，该方法实际的操作和计算机编程实现将非常容易和可行。

2.4连续两次修改

由式(14)得到第一次修改结构的近似特征值和特征值向量，并将其作为第二次修改重分析的初始特征值和特征向量，然后再执行式(6)～式(14)，就可得到第二次修改后结构的近似特征值和特征向量。粗略分析，第一次修改近似重分析的误差会累积到第二次修改的近似重分析中。两次重分析之间显然存在误差的转移和累积，但由于伪随机初始特征向量措施的实施，从第二次修改的近似重分析结果来看，误差并没有明显的增加，表明本文所提出的特征向量伪随机初始化方法一方面简化了以往新增加自由度上特征向量的初始化措施，另一方面有效的避免了两次近似重分析误差的累积。

2.5误差定义

定义特征值相对误差(Relative error)：

(15)

式中,精确特征值λei是直接求解拓扑修改结构的特征方程得到的，λai是采用所提出的独立耦合质量正交化处理近似方法计算得到的特征值, 同时给出近似特征向量与精确特征向量的夹角余弦值α, 也即模态置信因子(Model Assurance Criterion,MAC )来衡量近似特征向量和精确特征向量的相关性[8]，公式如下

(16)

式中,x，y分别表示直接计算得到的精确特征向量和CA方法间接求解得到的近似特征向量。MAC的值越接近1，表明两向量的相关性就越好；反之，MAC的值越接近0，表明两向量的相关性越差，也即近似特征向量的逼近质量越差。Massa[6]曾指出，MAC的值在0.7～1之间就表明近似特征向量与精确特征向量具有良好的相关性。

3数值算例

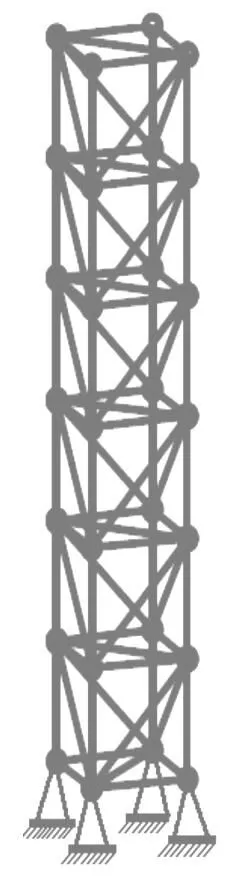
图1　初始结构Fig.1 The original

图2 148杆拓扑结构(第一次修改)Fig.2148-bartopologystructure(thefirstmodification)图3 161杆拓扑结构(第二次修改)Fig.3161-bartopologystructurestructure(thesecondmodification)

表1　采用不同方法得到的连续两次拓扑修改结构前五阶特征值及特征向量的比较

对于算例1，从表1可以看出，即便是对于连续两次修改的拓扑大修改的动力学重分析问题，采用本文方法也能得到修改后新结构的高精度的近似特征值和特征向量。

在相同的计算环境和平台下，经多次运算，直接重分析分析和近似重分析平均计算费用的比较如下：整个精确直接重分析计算需用时0.166 4 s，本文整个近似方法重分析计算需用时0.003 768 s，节省近97.8%的计算费用。由于采用了特征向量伪随机初始化方法，将使得重分析计算在优化设计中的可操作性大大简化和加强。而且可以预见，本文所提出的方法对于减少拓扑优化设计的计算量将是相当可观的。

例3-2考虑如图4所示的弯曲薄板结构，假定板的材料参数为弹性模量E=2.1×1011Pa，质量密度为ρ=7 800 kg/m3。板的厚度为0.01 m, 泊松比为0.3。整个板长0.8 m, 宽0.4, 左端固支，其余端自由，有限元离散成3 321个节点和3 200个矩形单元。假设第一次拓扑修改的结果是增加1 640个节点及1 600个矩形单元，如图5所示；第二次拓扑修改的结果是增加820个节点及800个矩形单元，其它材料或者物理参数保持不变，如图6所示。

对于算例2，从表2可以看出，即便是对于连续两次修改的拓扑大修改的动力学重分析问题，采用本文方法也能得到修改后新结构的高精度的近似特征值和特征向量。

图4　初始的悬臂弯曲板结构Fig.4 The original cantilevered bending plate structure

图5　第1次修改的拓扑结构Fig.5 The topology structure by the first modification

图6　第2次修改的拓扑结构Fig.6 The topology structure by the second modification

模态λeiλciRe1λuiRe2λdiRe3λtiRe4MAC417.47E+2007.86E+2005.177.60E+2001.697.49E+2003.31E-0017.48E+2001.15E-0020.821722.92E+4004.35E+40049.093.83E+40031.273.55E+40021.472.95E+4001.020.820533.80E+4005.05E+40032.974.02E+4005.874.54E+40019.543.86E+4001.580.769442.30E+5007.15E+500210.285.37E+500133.013.80E+50065.292.34E+5001.730.8092

在相同的计算环境和平台下，经多次运算，直接重分析分析和近似重分析平均计算费用的比较如下：整个精确直接重分析计算需用时1.832 6 s，本文整个近似方法重分析计算需用时0.537 8 s，节省近70.6%的计算费用。

4结论

本文针对这类新的涉及连续两次修改的结构拓扑大修改的动力学重分析问题，基于我们提出的独立和耦合质量正交化处理措施和特征向量伪随机初始化方法，再结合瑞利-里兹分析法，形成了一种高效、高精度的近似动力学拓扑重分析方法。数值算例的结果表明，所提的方法对解决新问题是十分有效的，且方法简便易实施，而且该近似重分析方法在保证计算精度的同时，近似结果又具有随机性。

参 考 文 献

[1] Amir O, Sigmund O, Lazarov B S, et al. Efficient reanalysis techniques for robust topology optimization[J].Computer Methods in Applied Mechanics and Engineering, 2012, 245/246: 217-231.

[2] Chen Su-huan, Ma Liang, Meng Guang-wei, et al. An efficient method for evaluating the natural frequencies of structures with uncertain-but-bounded parameters[J].Computers and Structures, 2009, 87: 582-590.

[3] Kaveh A, Fazli H. Approximate eigensolution of locally modified regular structures using a substructuring technique[J].Computers and Structures, 2011, 89: 529-537.

[4] Ma Liang, Chen Su-huan, Meng Guang-wei. Combined approximation for reanalysis of complex eigenvalues[J].Computers and Structures, 2009, 87: 502-506.

[5] Cacciola P, Muscolino G. Reanalysis techniques in stochastic analysis of linear structures under stationary multi-correlated input[J].Probabilistic Engineering Mechanics, 2011, 26: 92-100.

[6] Massa F, Tison T, Lallemand B. Structural modal reanalysis methods using homotopy perturbation and projection techniques[J].Computer Methods in Applied Mechanics and Engineering, 2011, 200: 2971-2982.

[7] Kashiwagi M. A numerical method for eigensolution of locally modified systems based on the inverse power method[J].Finite Elements in Analysis and Design, 2009, 45: 113-120.

[8] 邸娜,陈力奋,王皓. 非亏损系统二次特征值问题的Ritz降阶法[J].振动与冲击, 2002, 21(4)：80-84.

DI Na, CHEN Li-fen, WANG Hao. Ritz reduced method for quadratic eigenproblems of non-defective systems[J].Journal of Vibration and Shock, 2002, 21(4)：80-84.

[9] Kirsch U. Combined approximations—a general reanalysis approach for structural optimization[J].Struct Multidisc Optim, 2000, 20: 97-106.

Structural topology reanalysis for twice continuous modifications based on pseudo-random eigenvector

HEJian-jun,CHENXiang-zi(School of Automobile and Mechanical Engineering, Changsha University of Science and Technology, Changsha 410004, China)

Abstract:According to the problem of structural dynamic topological reanalysis for two continuous modifications, a new method for dynamic reanalysis of topological modified structure with added degrees and twice-continuous modifications was proposed in this paper.This method is a combined independent mass-orthogonalization strategy and a pseudo-random numbers initialization eigenvector method with Rayleigh-Ritz analysis.Compared with the direct finite element analysis, computational cost can be significantly reduced by this method, which is also easy to operate and implement.The numerical example shows that the proposed method for dynamic topological reanalysis of twice-continuous modifications is effective and has high precision.

Key words:twice continuous modifications; dynamic topological reanalysis; pseudo-random; mass orthogonalization

中图分类号:O342

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.033

收稿日期：2014-12-25修改稿收到日期：2015-03-25

基金项目：国家自然科学基金项目(51305048);湖南省高等学校科学研究一般项目(11C0045);谢亿民“湖湘学者”子课题资助

第一作者 何建军 男，博士, 讲师，1979年生

E-mail: hezhengde8@163.com