基于人工鱼群算法的随机结构AMD控制系统LQR权矩阵优化

王　磊, 谭　平, 李森萍(广州大学 工程抗震研究中心,广州　510405)



基于人工鱼群算法的随机结构AMD控制系统LQR权矩阵优化

王磊, 谭平, 李森萍(广州大学 工程抗震研究中心,广州510405)

摘要：针对随机结构在平稳随机激励下线性二次最优控制的权参数选取问题，提出了基于人工鱼群算法的随机结构AMD控制系统权矩阵优化设计方法。该方法以结构随机响应和控制力均方值的加权组合为目标函数，考虑了结构和外激励的随机性对于控制效果的影响。其优化结果不仅保证了控制器的控制效果，而且降低了控制效果对于随机参数的敏感性，增强了控制器的鲁棒性。最后结合数值算例，验证了所述方法的有效性和正确性。

关键词：随机结构;权矩阵;主动质量阻尼器;鱼群算法

线性二次型经典最优控制算法(Linear Quadratic Optimal Control,LQR)因其性能指标物理意义明确，最优控制解可以解析表达，易于实现闭环反馈控制，而被广泛运用于结构振动控制之中[1-4]。LQR控制器的控制效果直接取决于加权矩阵的选取，如果加权矩阵选取不当，则可能造成控制装置不能发挥最优性能，造成资源浪费，甚至对结构响应产生不利的影响。对于权矩阵的选取较常用的为试探法，即选择不同的权矩阵比较计算选取最优值。此种方法一般仅能得到局部最优解。鉴于此，发展了多种优化权矩阵的方法。郭一峰等[5-6]基于遗传算法采用不同的目标函数对权矩阵进行了优化，其优化后的控制效果都满足设计和结构性能的要求；张葛祥等[7]利用参数满意度对权参数进行了优化，综合考虑了控制性能和能量间的关系；祁皑等[8]提出了一种新的权矩阵选择方法，并详细分析了权矩阵参数对控制效果的影响；杨刚等[9]提出了仅包含一个可调参数的新目标函数，并利用非线性优化理论对该目标函数进行了优化分析。在以往的研究中，对于权矩阵的优化大多集中于确定性结构在特定激励下的分析。然而在实际环境之中，存在着大量的不确定性，仅对特定激励下确定性结构进行权矩阵优化，忽略结构和外部环境激励的随机性对于控制效果的影响，其优化结果仍具有一定的局限性，难以全面表现控制装置对于结构响应的控制效果。

本文基于人工鱼群算法，对随机地震下随机结构AMD控制系统的权矩阵进行了参数优化。其中对于结构参数和环境激励的随机性造成的复合随机问题，首先通过结构响应对随机参数灵敏度分析，合理的确定结构随机参数，进一步利用Gegenbauer多项式将含λ-PDF分布随机变量的随机结构化为等效扩阶系统，采用Kanai-Tajimi地震动模型为地震动输入，计算结构随机响应。最后结合数值算例验证了所提方法的有效性及所优化参数的鲁棒性。

1随机结构控制系统正交分解

对于随机结构AMD振动控制系统，其动力平衡方程为

Ks(θ)Xs=-MsIf(t)+HfTMD

(1)

(2)

fTMD=kT(xT-xn)+cT(xT-xn)-u(t,θ)

(3)

控制力u(t)可采用LQR控制算法进行设计,以层间位移为控制目标。首先定义二次性能泛函为：

(4)

式中：Z(t)=[d1,d2,…,dn]T，其中di为结构的第i层层间位移，Q为半正定矩阵，R为正定矩阵。

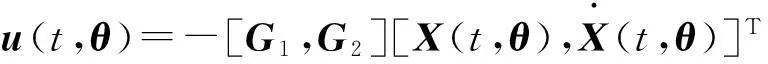
不失一般性，假设式(1)中结构控制系统的质量、阻尼和刚度有下列形式[12]

(5)

(6)

(7)

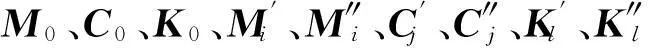
(8)

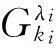
把式(5)～式(8)代入式(1)利用正交多项式逼近理论，得到其确定性系统如下

ui=0,1,…,nii=1,…,N

(9)

2随机结构响应灵敏度

对于式(5)～式(7)所示的结构随机质量、阻尼和刚度矩阵可分解为均值分量和零均值随机分量之和：

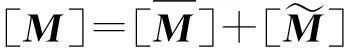
(10)

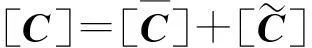
(11)

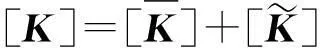
(12)

随机结构中的随机变量也能分解为

(13)

则式(1)所示随机结构响应亦可做同样分解

(14)

(15)

若已知随机结构各个参数的分布参数，利用摄动法通过式(15)求解结构随机响应对于各个随机参数的灵敏度，从而以灵敏度为依据来选取结构随机变量，可有效降低随机变量选取的盲目性和不确定性。

3基于人工鱼群算法的权矩阵优化

人工鱼群算法是李晓磊等[13]提出的一类基于动物行为的群体智能优化算法。该算法通过模拟鱼类的觅食、聚群、追尾、随机等行为在搜索区域中进行寻优，是一种群智能算法。其具有并行性、简单性、能很快跳出局部极优值、寻优速度快、对初值不敏感等特点。本文利用人工鱼群算法，对权矩阵进行参数优化，其优化流程如图1所示。

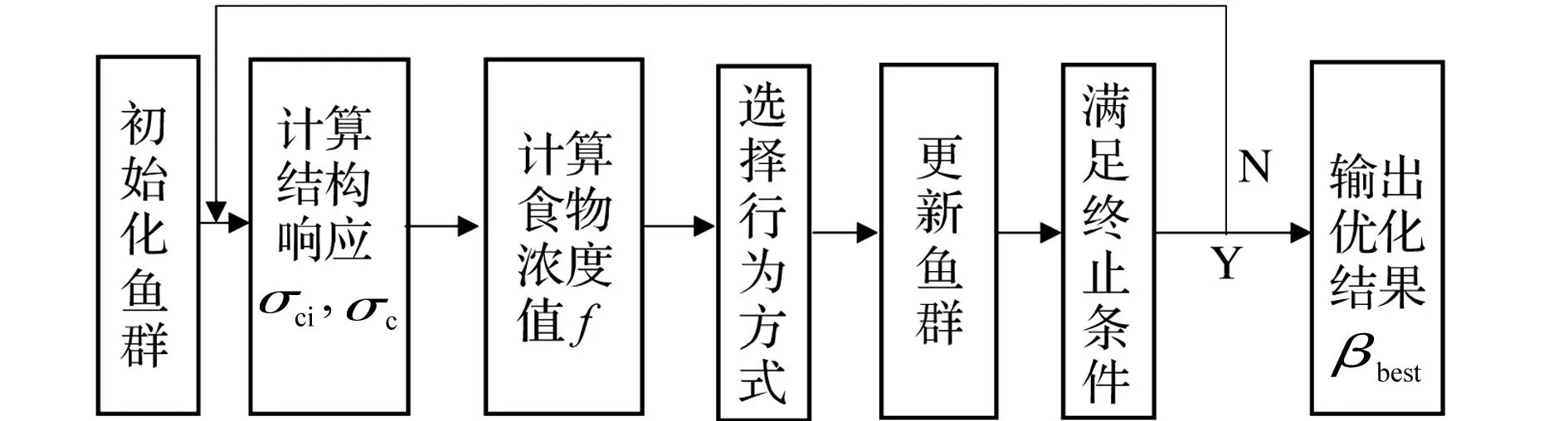
图1　人工鱼群算法优化流程图Fig.1 Flow chart for weighting matrices using artificial fish algorithm

结构在地震作用下的性能很大程度上取决于结构各层的层间位移，因此在本文中所设计AMD系统主要的控制对象选取为结构层间位移，权矩阵设定为Q=10βI，R=1，其中β为待优化参数。对于实际工程，控制系统的输入能量一定是有界的，为了实现前述控制目标并兼顾能量消耗，本文定义食物浓度函数(目标函数)如下

(16)

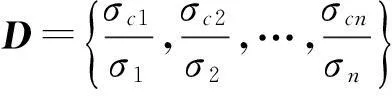
4仿真分析

4.1算例模型

三层剪切型随机结构，其结构参数如表1所示，其中对于结构质量参数，由于在实际工程中其变异系数常常较小，所以被考虑为确定性参数。

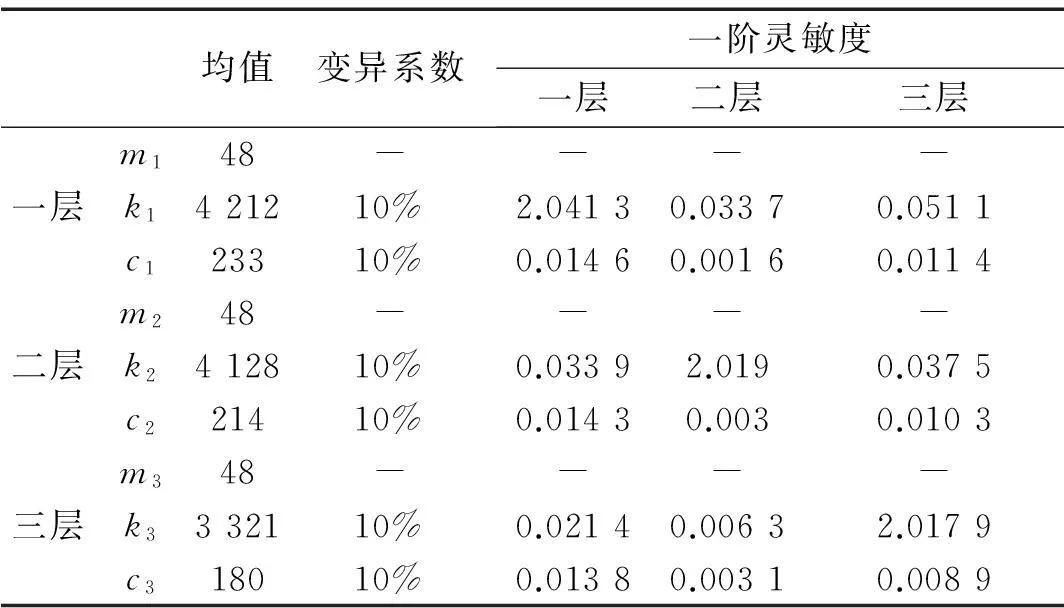
表1　结构随机参数

注：质量、刚度、阻尼单位分别为：t, kN/m, kN·s/m.

4.2随机参数灵敏度分析

表1中结构随机参数对于结构层间位移响应均方值的一阶灵敏度为式(13)计算结果的绝对值，对于式(13)利用摄动法求解(摄动步长为0.01σ，σ为随机参数的标准差)。由各随机参数灵敏度分析可知：① 刚度对于结构各层层间位移均方值的影响较阻尼的影响大；② 各层刚度的随机变化都对本层的层间位移均方值有较大影响，对其他各层影响程度较小且基本相当；③ 各层阻尼的随机变化对层间位移均方值影响规律相同：对一层影响最大，三层次之，二层最小。依据以上分析，后文在对于控制系统权矩阵优化时仅考虑一、二层刚度为随机参数，其分布如图2所示，其中一层刚度变异系数为8%，二层为7%，其概率密度函数如下所示

(17)

图2　概率密度曲线Fig.2 PDF curve

4.3权矩阵优化

人工鱼群算法最终优化结果为β=15.013，其优化过程和优化前后鱼群在 [10,16,-3,0]区域内分布分别如图3、4所示，由图可知鱼群算法对本文优化目标收敛快、计算效率高，在优化的初始，鱼群的分布较为均匀，随着优化的进行，鱼群通过觅食、聚群、追尾、随机等行为逐渐向最优值靠拢，寻优过程相对简单、快捷，特别是由于考虑了鱼群的拥挤度因子，将会有少数人工鱼分布在次优值附近，所以人工鱼群算法较其他优化算法容易跳出优化函数局部最优值的影响从而得到函数的全局最优值。

图3　优化过程Fig.3 Optimization process

图4　人工鱼分布Fig.4 Artificial fish distribution

参数量值参数量值ωg/(rad·s-1)15.6mt(t)1.44ξg0.6kt/(kN·m-1)23.7S0/(cm2·s-3)15.74ct/(kN·s·m-1)0.7

表4对比了无控、TMD控制、AMD控制结构的层间位移均方根。由表4分析可知，相对于无控结构，主、被动控制系统对于随机结构层间位移响应均方根都具有一定的控制效果。但是由于参数的不确定性，特别是结构参数随机性的影响，TMD对于随机结构响应的控制效果不明显。但是由于主动控制力的引入，AMD控制效果较TMD有较大的提高，AMD能更有效地降低结构各层层间位移响应，减小结构在外激励下的损伤。因此，采用本文所述鱼群算法优化的权矩阵，在综合考虑了控制能量的前提下，取得了较好的控制效果，增大了控制系统对于外界不确定因素的鲁棒性，降低了控制效果对于随机参数的敏感性，增强了结构的安全性与鲁棒性。

表3　人工鱼群算法参数

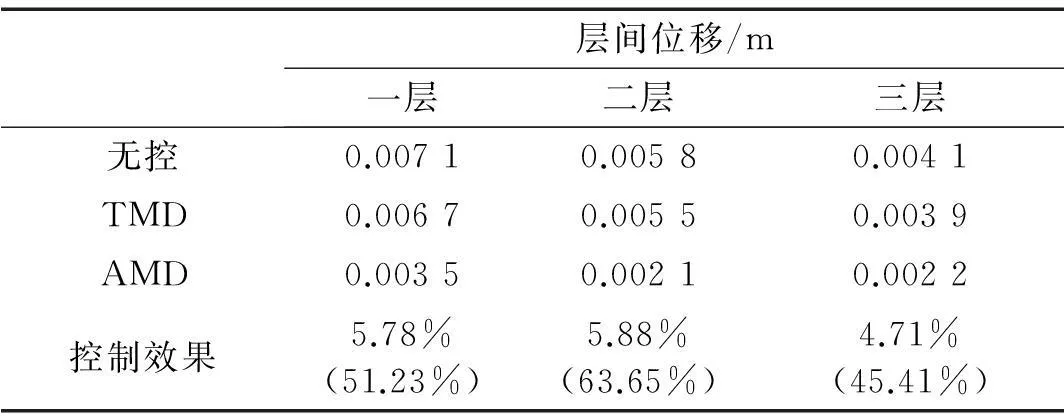
表4　结构响应均方根

注:控制效果中括号内外分别为AMD和TMD的控制效果。

5结论

本文在充分考虑了外激励和结构参数随机性的影响下，利用鱼群算法对随机结构AMD控制系统的LQR权矩阵进行了优化分析，得到了如下一些结论：

(1) 实际工程之中参数的不确定性是不可避免的，在合理设计控制系统时应充分考虑结构参数和外激励的随机性。本文提出的基于人工鱼群算法的LQR权矩阵优化设计方法，不依赖于特定的外激励时程，能有效减小结构层间位移响应的均方根，降低AMD系统控制效果对于随机参数的敏感性，提高AMD控制系统的鲁棒性，具有重要的理论意义和工程应用前景；

(2) 人工鱼群算法对LQR权矩阵优化过程表明其具有简单高效、不易陷入局部最优、对初值不敏感的特点；

(3) 对于结构随机参数敏感性分析表明，相较于阻尼，刚度的随机变化对结构响应的影响更大；各层刚度随机变化对各层层间位移均方根的影响规律为：对本层影响最大，其他各层影响次之且程度基本相当；对于各层阻尼的随机变化，其对于结构层间位移影响规律基本相同：对一层影响最大，三层次之，二层最小；

(4) 仿真分析结果表明，权矩阵优化后AMD对于随机结构响应的控制效果优于TMD，在综合考虑能量消耗的条件下,AMD能有效降低结构的层间位移响应，增大结构的安全性，使结构性能满足设计要求。

参 考 文 献

[ 1 ] Ghaffarzadeh H, Younespour A.Active tendons control of structures using block pulse functions[J].Structural Control and Health Monitoring, 2014,21:1453-1464.

[ 2 ] Ambrosio P, Cazzulani G, Resta F, et al.An optimal vibration control logic for minimizing fatigue damage in flexible structures[J].Journal of Sound and Vibration,2014, 333:1269-1280.

[ 3 ] Gagge F L A,Da Conceicão S M, Vasques C H,et al.Experimental identification and control of a cantilever beam using ERA/OKID with a LQR Controller[J].Journal of Control, Automation and Electrical Systems, 2014,25:161-173.

[ 4 ] 符川,屈铁军,孙世国.动调频液柱阻尼器基于遗传算法的LQR控制优化设计[J].振动与冲击,2015,34(2):210-214.

FU Chuan,QU Tie-jun,SUN Shi-guo.Optimal design of ATLCD with LQR control based on genetic algorithm[J].Journal of Vibration and Shock, 2015, 34(2):210-214.

[ 5 ] 郭一峰，徐赵东，涂青，等.基于遗传算法的LQR算法中权矩阵的优化分析[J].振动与冲击，2010,29(11)：217-220.

GUO Yi-feng, XU Zhao-dong, TU Qing,et al.Optimal analysis for weight matrices in LQR algorithm based on genetic algorithm[J].Journal of Vibration and Shock, 2010,29(11)：217-220.

[ 6 ] Jiang Bo, Wei Xin-jiang, Guo Yan-ying.Linear quadratic optimal control in active control of structural vibration systems[C]//2010 Chinese Control and Decision Conference.Xuzhou,China,2010.

[ 7 ] 张葛祥，金炜东，胡来招.多变量系统控制器的参数满意优化设计[J].控制理论与应用，2004,21(3)：362-366.

ZHANG Ge-xiang, JIN Wei-dong, HU Lai-zhao.Parameters satisfactory optimization of controller in multivariable control system[J].Control Theory and Applications, 2004,21(3)：362-366.

[ 8 ] 祁皑，李惠.主动质量控制系统的权矩阵选择及其参数的敏感性分析[J].土木工程学报，2003,36(11)：93-98.

QI Ai, LI Hui.Selection of weight matrix and sensitivity analysis of parameters in active mass damper system[J].China Civil Engineering Journal, 2003,36(11)：93-98.

[ 9 ] 杨刚，姚华.实用航空发动机LQR权阵选取方法[J].南京航空航天大学学报，2006,38(4)：403-407.

YANG Gang, YAO Hua.Choosing method for aeroengine LQR weighting[J].Journal of Nanjing University of Aeronautics and Astronautics, 2006,38(4)：403-407.

[10] Li Jie, Chen Jian-bing, Fan Wen-liang.The equivalent extreme-value event and evaluation of the structural system reliability[J].Structural Safety, 2007, 29: 112-131.

[11] Spencer Jr B F, Dyke S J,Deoskar H S.Benchmark problems in structural control: Part I—active mass driven system[J].Earthquake Engineering and Structural Dynamics, 27(11), 1998, 1127-1139.

[12] Wu Cun-li, Ma Xiao-ping, Fang Tong.A complementary note Gegenbauer polynomial approximation for random response problem of stochastic structure[J].Probabilistic Engineering Mechanics, 2006, 21:410-419.

[13] 李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践，2002，22(11)：32-38.

LI Xiao-lei, SHAO Zhi-jiang, QIAN Ji-xin.An optimizing method based on autonomous animats: fish-swarm algorithm[J].Systems Engineering—Theory and Practice,2002，22(11)：32-38.

[14] Soong T T, Dargush G F, Passive energy dissipation systems in structural engineering[M].Chichester :Wiley, 1997.

Optimal analysis of weight matrices of LQR algorithm for stochastic structure-AMD system based on artificial fish algorithm

WANGLei,TANPing,LISen-ping(Earthquake Engineering Research and Test Center, Guangzhou University, Guangzhou 510405, China)

Abstract:In allusion to the choice of the weight matrices Q and R in LQR algorithm in the stochastic structure-AMD system under stationary random excitation, the optimization method of the weight matrices is proposed based on the artificial fish algorithm.The method resolves the weight matrices optimization via the objective function with the weighted root mean square of the stochastic structural responses and active control force, taking into account the effect of the randomness in the structure and excitation on the control effect.The effectiveness and validity of the procedures of the optimal designs of the weight matrices are proven by a numerical example.Numerical results preliminarily show that the optimized weight matrices can effectively suppress undesirable vibration, reduce the sensitivity of the control effectiveness to the random parameters and improve the robustness of AMD.

Key words:stochastic structure; weight matrix; active mass damper(AMD); artificial fish algorithm

中图分类号:TU352

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.024

通信作者谭平 男，博士，研究员，博士生导师，1973年生

收稿日期：2014-11-06修改稿收到日期：2015-04-21

基金项目：国家基金项目(91315301-07;51408142)；国家教育部长江学者创新团队项目(IRT13057)

第一作者 王磊 男，博士生，1987年生