基于加速度二次协方差矩阵参数变化比法的环境振动下结构损伤识别

王立新, 李雪艳, 姜　慧, 朱嘉健(.中国地震局地震监测与减灾技术重点实验室 广东省地震局，广州　50070；.暨南大学 力学与土木工程系, 广州　5063)



基于加速度二次协方差矩阵参数变化比法的环境振动下结构损伤识别

王立新1, 李雪艳2, 姜慧1, 朱嘉健1(1.中国地震局地震监测与减灾技术重点实验室 广东省地震局，广州510070；2.暨南大学 力学与土木工程系, 广州510632)

摘要：在白噪声环境激励下，结构加速度响应的自相关/互相关函数构成一个新的二次协方差(CoC)矩阵，组成这一协方差矩阵的元素经证明是结构模态参数(频率、振型、阻尼)的函数；与提取模态参数的一般损伤识别方法相比，二次协方差矩阵包含结构振动的更多和更高阶模态信息。利用结构损伤前和损伤后的二次协方差(CoC)矩阵参数的变化比，对只基于振动输出的、环境振动下的结构进行损伤识别。对一个七层框架结构模型进行了数值模拟，首先对不同噪声程度、不同损伤位置和程度的损伤结构进行损伤定位，再结合模型修正法，对结构损伤程度进行识别，展示了该方法的有效性。

关键词：损伤识别；二次协方差矩阵；环境激励

基于环境振动的工程结构健康监测，具有无须贵重的激励设备，不中断结构的正常使用，方便省时，价格低廉，只需测定响应数据等优点[1-6]；避免了在使用激振设备过程中对结构造成损伤，提高了安全性，测试环境符合结构的边界条件和实际工况，能够更为真实准确地反应结构在工作状态下的振动特性[5,7]。Li等[8]提出了白噪声激励条件下的加速度响应二次协方差(CoC)矩阵，经证明该矩阵的元素仅是结构模态参数(频率、振型、阻尼)的函数。这一方法的显著优点表现在，首先，仅利用加速度响应即可计算，不需进行模态识别，避免了在模态参数识别中可能带来的功率谱泄露、密集模态丢失、截断误差等问题；第二，该方法可以避免时域方法的系统定阶问题；第三，理论上CoC矩阵所包含的模态阶数只受限于数据采样频率，也就是可以尽量多地包含更多阶数的模态信息，避免丢失响应信号中与损伤有关的高阶模态，使得提取的损伤指标更加灵敏。本文将利用基于该二次协方差矩阵参数变化比的方法来对一环境激励下的七层框架结构进行损伤识别。

1加速度响应二次协方差矩阵参数变化比方法的基本原理

支座激励下的N自由度黏性阻尼结构系统的运动方程为：

(1)

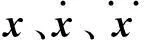
(2)

从式(2)计算出矩阵u(p)·(u(p))T为[8]：

(3)

式中下标i×j表示为矩阵[u(p)·(u(p))T]的第i行j列的单元，i与j是结构的模态阶数，Δt是采样步长，S是反应白噪声激励能量水平的常数，其它参数的细节见参考文献[8]。

假设加速度计安装在监测结构上，在白噪声激励下连续记录监测点的加速度响应，监测得到的加速度响应二次协方差矩阵通过下式计算为：

(4)

式中,E表示为期望值，式(4)中CoC矩阵Tp可以直接通过加速度响应的协方差矩阵Rp=[Rpl1(t)Rpl2(t) …Rplm(t)]T计算得到。

假设结构在位置r处发生了损伤，这个损伤在结构的刚度上用刚度矩阵的改变ΔK来表征，那么结构发生损伤后的第i个CoC矩阵参数的改变量ΔCi就是损伤的位置向量r和刚度矩阵的改变ΔK的函数[12]，

ΔCi=fi(ΔK,r)

(5)

把该函数对没有损伤的情况(ΔK=0)进行展开，并忽略高阶项，得到

(6)

当结构没有发生损伤时，刚度矩阵的改变ΔK=0，所以对于所有可能的r来说，没有损伤时，fi(0,r)=0，因此式(6)变为，

ΔCi≈ΔK×gi(r)

(7)

同样的对第j个CoC矩阵参数的改变量ΔCj,有，

ΔCj≈ΔK×gj(r)

(8)

所以由式(7)和式(8)有，

(9)

由式(9)得出结论：当结构发生损伤后，任意某两个CoC矩阵参数改变量的比值仅是损伤位置的函数，而与损伤的大小没有关系，并且随着损伤位置的不同，这个CoC矩阵参数变化比的比值也会变化，那么利用实测出的结构发生损伤后的“CoC矩阵参数变化比”便可以识别出结构发生损伤的位置。

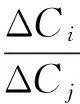
需要注意的是，上述从式(5)～式(9)的推导过程中引入了近似，式(6)中截去了高阶非线性项从而引入了截断误差。如果被截去的高阶非线性项在函数ΔCi中占的分量不大的话，也就是说ΔCi是关于参数ΔK的线性或者弱非线性函数，那么式(6)对式(5)的近似误差较小，后续式(7)中的误差也在可接受的范围内，这将会是一个影响后续基于该指标的损伤识别是否成功的关键因素。因此，在实际结构的分析中，需要事先研究ΔCi与ΔK的关系，从而确定所提出的方法是否适用，这一点在下文第2节会进一步讨论。

2CoC矩阵参数变化比方法的数值模拟

基于CoC矩阵参数变化比方法，对一个七层框架结构模型进行损伤识别。结构模型如图1所示，该结构被划分为70个欧拉梁单元，共65个节点，节点排列如图 1所示，其中左边竖向柱(第1～第21单元)的横截面积为2.425×10-4m2,截面惯性矩为4.753 5×10-10m4,密度为7 850 kg/m3；横向梁(第22～第49单元)的横截面积为4.46×10-4m2，截面惯性矩为2.957 2×10-9m4,密度为7 734.2 kg/m3；右边竖向柱(第50～第70单元)的横截面积为2.425×10-4m2，截面惯性矩为4.753 5×10-10m4,密度为7 850 kg/m3。材料的弹性模量E为2×1011N/m2。在节点23、25、26、28、29、31、32、34、35、37、38、40、41、43处添加一重为3.8 kg的铁块。结构底部为固支约束，理想白噪声激励施加在结构的支座上，大小为0.01 m2/s4。在该模拟计算中，节点2，5，8，11，14，17和20处的水平和竖直方向的加速度通过Newmark数值方法计算得出，用来模拟实际结构中测试得到的加速度响应，并用来计算实验二次协方差(CoC)矩阵。

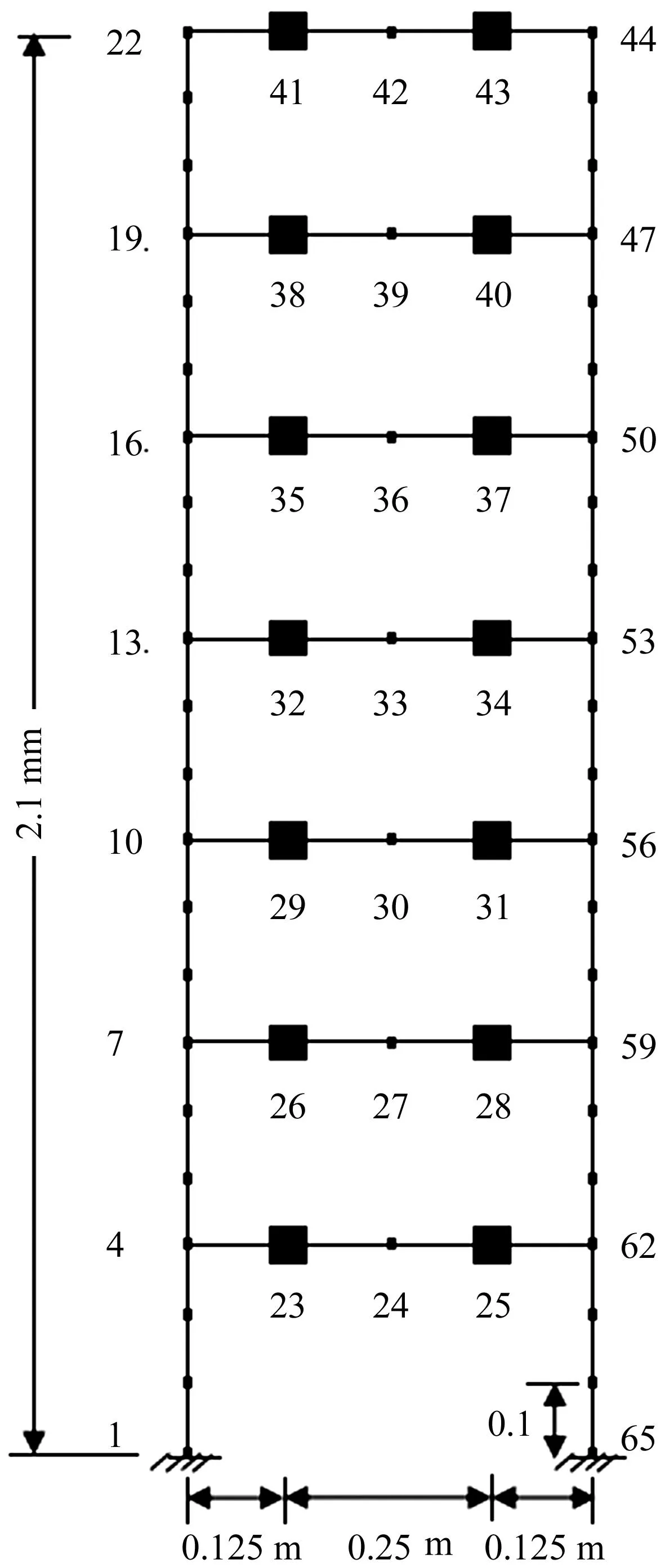
图1　七层框架结构模型Fig.1 The 7-story frame structure model

首先模拟单元26的刚度依次下降 5%、10%、…、85%，计算出每种损伤程度状态下的“CoC矩阵参数变化比”。由于CoC矩阵是对称矩阵，为了简化数据，只取其对角线上的元素进行分析，由此得到结构的“CoC矩阵参数变化比”与单元不同程度损伤所对应的曲线见图2和表1，对单元49做同样计算可得到图3，图中均采用结构CoC矩阵对角线上元素和第1个对角元素的比值。可见，虽然并不是所有的ΔCi/ΔCj随损伤程度变化的曲线都是绝对水平线，但是大部分曲线在一定损伤大小内(图2是50%，图3是60%)都是接近水平线的，由此表明两个CoC矩阵参数改变量的比值ΔCi/ΔCj在一定损伤程度内，主要是由损伤位置决定，损伤大小对它的影响较小。也即说明，对于该模型结构，第1节式(6)中引入的近似是在可接受的范围内，从而可以应用本文提出的损伤识别方法。

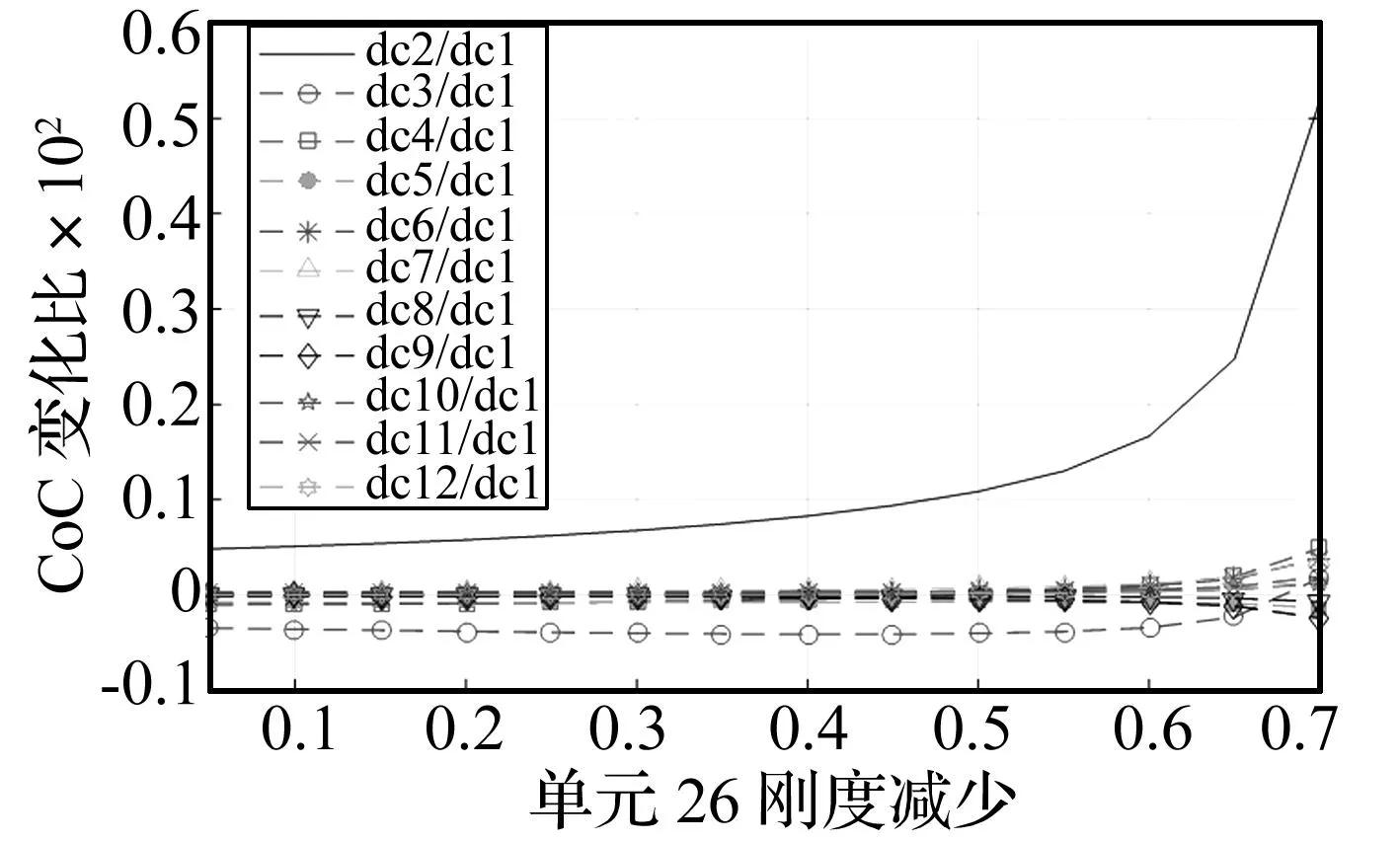
图2　单元26的刚度从5%减少到95%的CoC参数变化比曲线Fig.2 Curves of CoC parameters when the stiffness of Element 26 is reduced from 5% to 95%

图3　单元49的刚度从5%减少到95%的CoC参数变化比曲线Fig.3 Curves of CoC parameters when the stiffness of Element 49 is reduced from 5% to 95%

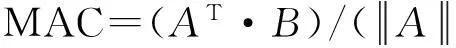
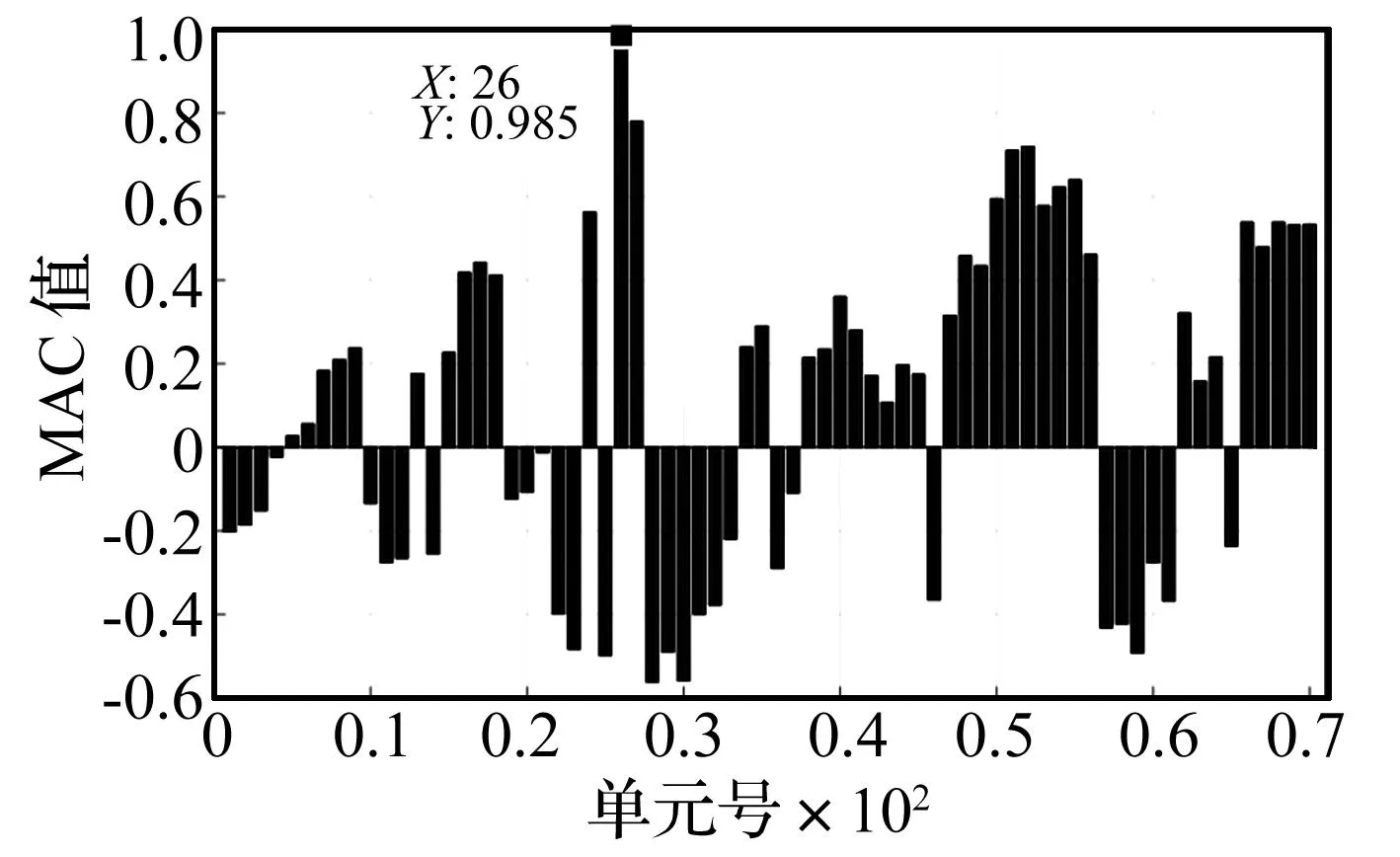
图4　单元26的刚度减少35%对应的“实测”CoC参数变化比向量与理论CoC参数变化比向量的的MAC值Fig.4 The‘measured’ and computed MAC values due to 35% stiffness reduction in Element 26

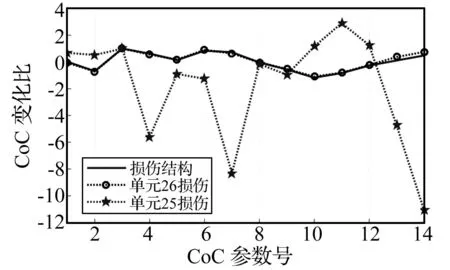
图5　单元26的刚度减少35%时“实测”和理论CoC参数变化比向量的比较Fig.5 Comparison of the‘measured’ and computed CoC change ratios due to 35% stiffness reduction in Element 26

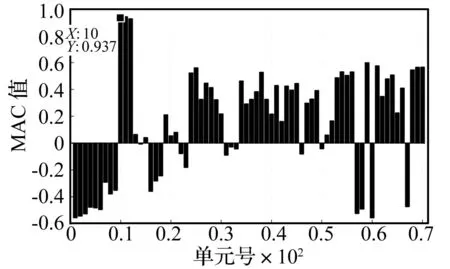
图6　单元10的刚度减少35%对应的“实测”CoC参数变化比向量与理论CoC参数变化比向量的的MAC值Fig.6 The ‘measured’ and computed MAC values due to 35% stiffness reduction in Element 10

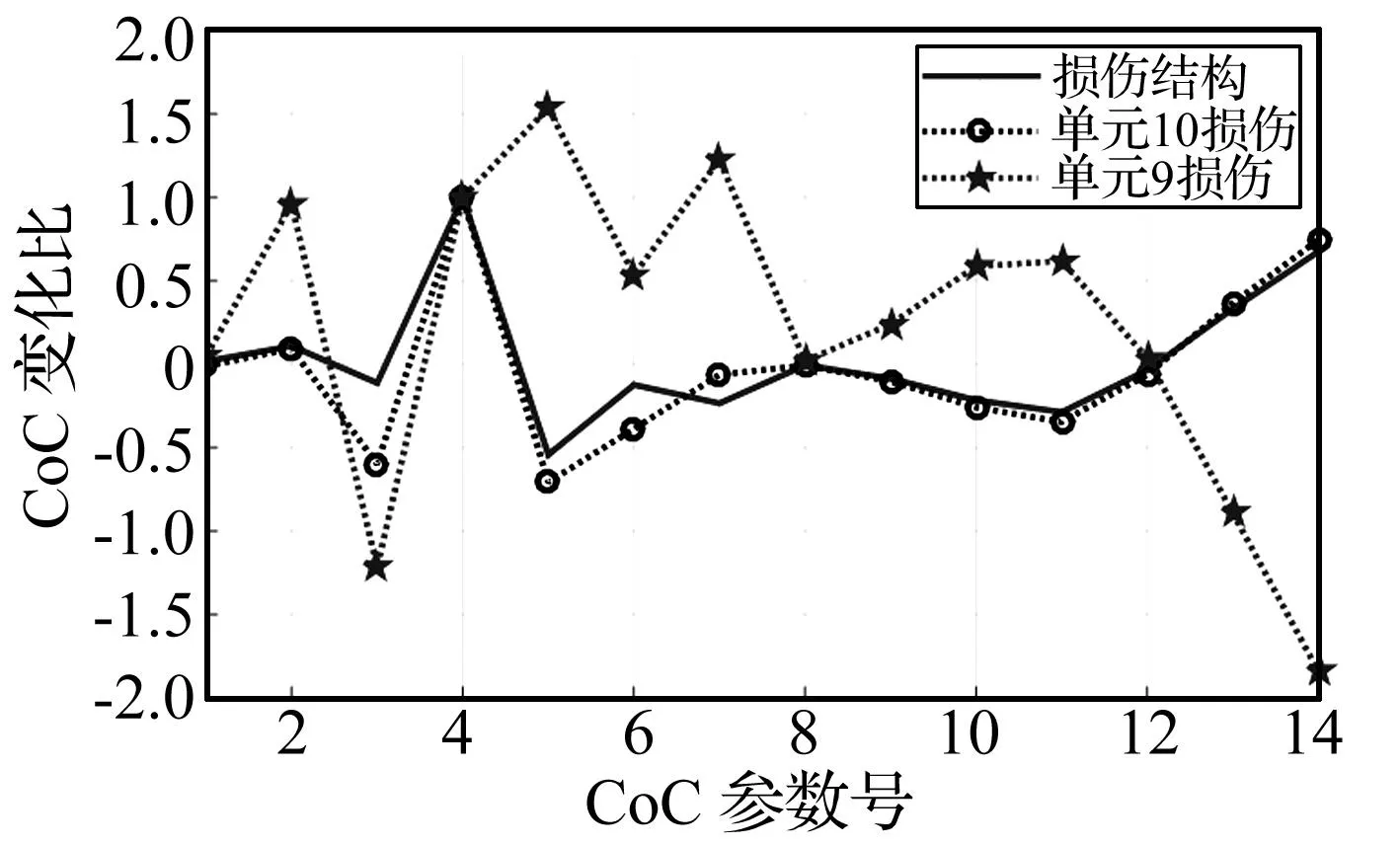
图7　单元10的刚度减少35%时“实测”的CoC参数变化比向量与理论的变化比向量的比较Fig.7 Comparison of the ‘measured’ and computed CoC change ratios due to 35% stiffness reduction in Element 10

综上所述，CoC矩阵参数变化比方法虽然无法识别出单元的损伤程度，但是可以识别出损伤位置；即使无法给出精确的损伤位置，也可以给出小范围的可能损伤位置，这样就能缩小潜在损伤单元的数目。本文再结合基于CoC灵敏度和模型修正方法便可以识别出损伤单元的损伤程度[8]。这里取损伤工况3为例进行计算，即单元10损伤30%和单元26损伤25%，在“实测”CoC矩阵参数变化比向量中加入15%的白噪声。首先通过CoC矩阵参数变化比法，可以把损伤范围从所有单元缩小到10个单元(根据MAC值的大小，取单元10,11，12，26, 38, 42, 48, 49, 51和52为最有可能损伤单元)，再利用CoC参数灵敏度和模型修正法，可以得出损伤向量如图8所示，可以看出，损伤位置和大小都能准确识别出。

因此，本文提出的基于CoC矩阵参数变化比向量缩小损伤范围，然后再精确识别损伤大小的二步法，可以提高模型修正法的耐噪声能力和提高其收敛速度，提高了方法的有效性。

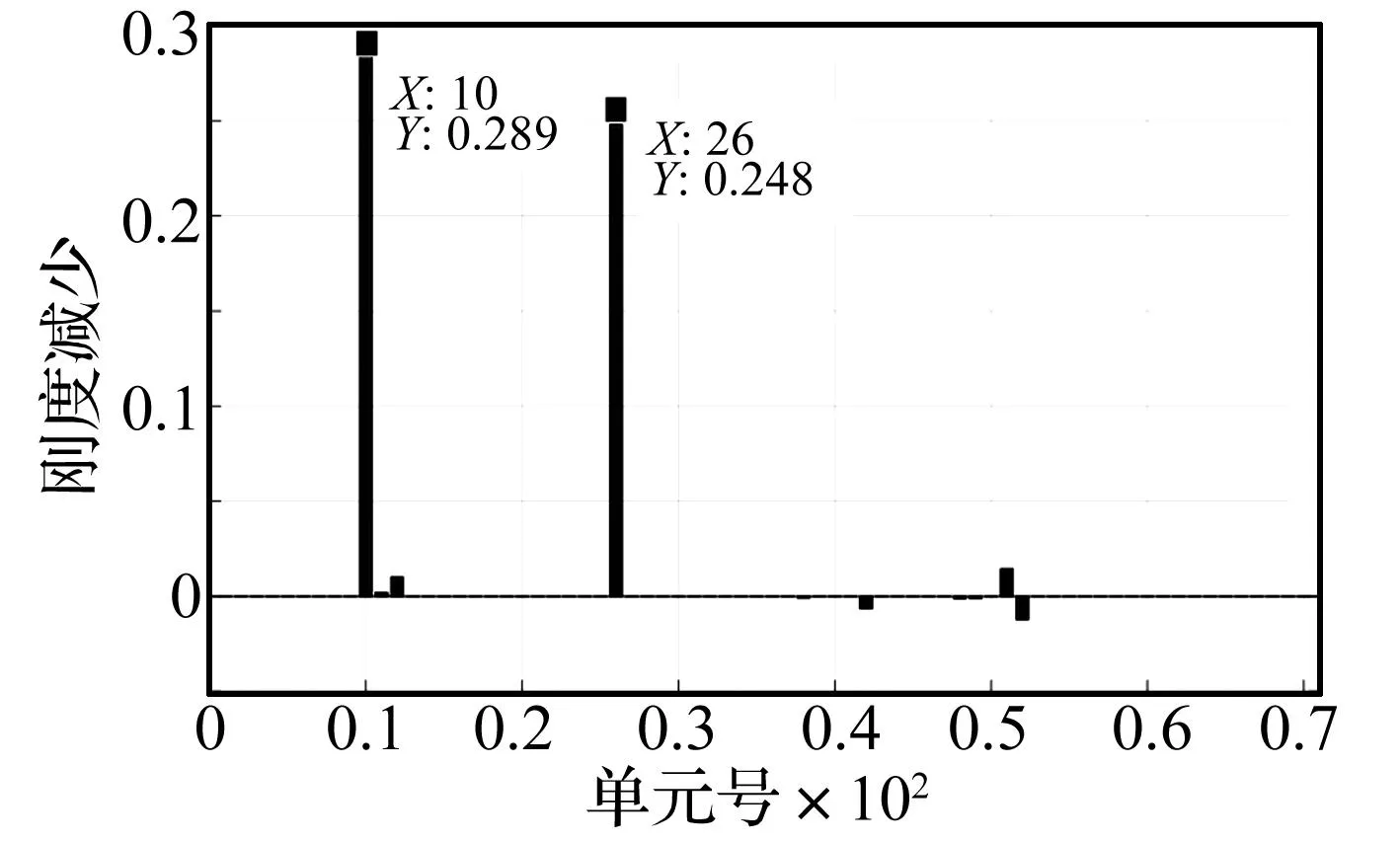
图8　单元10的刚度减少30%和单元26的刚度减少25%时通过二步法所识别出的损伤向量Fig.8 The obtained damage vector from the two-step method due to 30% stiffness reduction in Element 10 and 25% reduction in Element 2

本文提出的方法直接基于输出加速度响应进行结构损伤识别，计算简单，也避免了模态识别过程中可能产生的误差，但是应该看到，结构环境振动响应信噪比低，噪声的影响不可忽略。为了降低噪声的影响，本文在由加速度响应计算互相关函数Rpl(τ)时，要求有足够时间长度的加速度响应数据。因为在计算时是假定结构处于白噪声激励下的，这样才能把激励大小从互相关函数中去掉。但实际的环境激励不是理想的白噪声激励，所以对实际的环境振动响应数据，需要保证测试的加速度响应具有足够长的时间才能达到所需要的精度，这样的处理同时也降低了残留在加速度响应中的噪声影响。

另外需要说明的是，加速度响应协方差是结构模态参数(频率，振型和阻尼等)的函数，它是个全局参数，理论上，在某测点处发生的损伤，是能反应到其它测点加速度响应的协方差中的。但在实际使用中，由于测试加速度信号本身带有噪声，再加上方法误差，这些都会影响方法的准确性。采用更多测点可以在一定程度上纠正这些误差带来的误判，从而提高识别的准确性，所以本文中使用了比较多的测点。

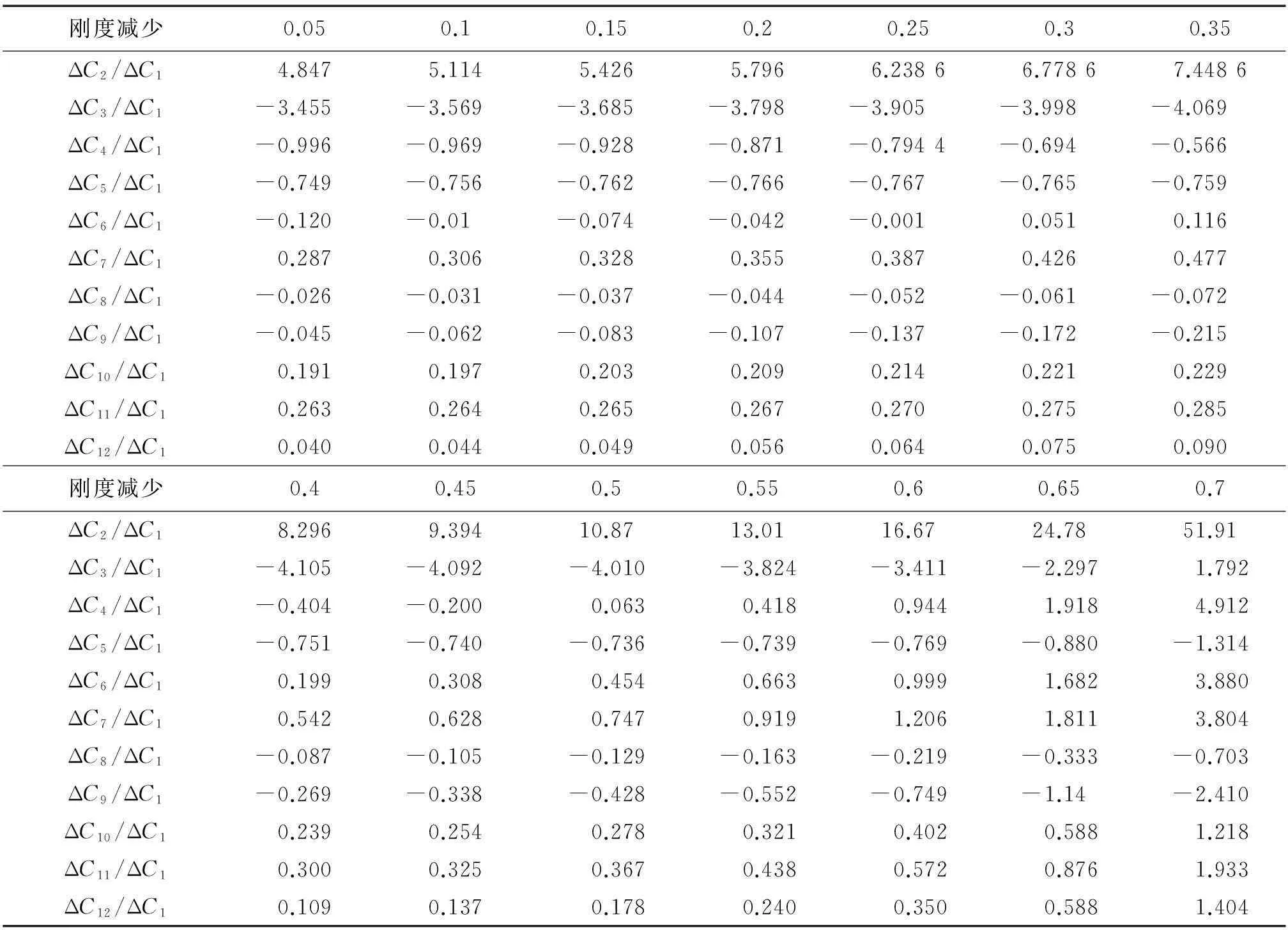
表1　第26个单元刚度不同程度减少时CoC参数变化比的变化

3结论

本文利用环境激励下的结构加速度响应二次协方差(CoC)矩阵参数变化比法，对结构进行损伤定位；再基于准确的定位或者缩小了的损伤识别区域，结合参数灵敏度和模型修正法，对结构进行损伤识别，并把该方法应用在一个七层框架结构上，通过计算分析，得到了满意的结果，展示了该方法的有效性和实用性。

参 考 文 献

[ 1 ] 任伟新.环境振动系统识别方法的比较分析[J].福州大学学报:自然科学版，2001，29(6)：80-86.

REN Wei-xin.Comparison of system identification methods using ambient vibration measurements[J].Journal of Fuzhou University:Natural Science, 2001, 29(6): 80-86.

[ 2 ] 王术新.姜哲.基于结构振动损伤识别技术的研究现状及进展[J].振动与冲击，2004，23(4)：99-102.

WANG Shu-xin, JIANG Zhe.Present developing situation and research advances in the field of structural damage detection[J].Journal of Vibration and Shock, 2004, 23(4): 99-102.

[ 3 ] Lee J J, Yun C B.Damage diagnosis of steel girder bridges using ambient vibration data[J].Engineering Structures, 2006, 28(6): 912-925.

[ 4 ] Siringoringo D M, Fujino Y.System identification of suspension bridge from ambient vibration response[J].Engineering Structures, 2008, 30: 462-477.

[ 5 ] 刘宇飞, 辛克贵, 樊健生,等.环境激励下结构模态参数识别方法综述[J].工程力学，2014, 31(4): 46-52.

LIU Yu-fei, XIN Ke-gui, FAN Jian-sheng, et al. A review of structure modal identification methods through ambient excitation[J].Engieering Mechanics,2014, 31(4): 46-52.

[ 6 ] 胡异丁,李丹, 任伟新,等.基于延时随机子空间方法的非白噪声环境激励结构模态参数识别[J].振动与冲击，2015, 34 (8):71-76.

HU Yi-ding,LI Dan,REN Wei-xin,et al.Modal parameter identification of structures under non-white noise ambient excitations using delay-index-based stochastic subspace method[J].Journal of Vibration and Shock,2015, 34 (8):71-76.

[ 7 ] 禹丹江.土木工程结构模态参数识别——理论、实现与应用[D]．福州：福州大学，2005.

[ 8 ] Li X Y, Law S S.Matrix of the covariance of covariance of acceleration responses for damage detection from ambient vibration measurements[J].Mechanical Systems and Signal Processing, 2010, 24(4): 945-956.

[ 9 ] Bendat J S, Piersol A G.Engineering applications of correlation and spectral analysis[M].New York: Wiley, 1993.

[10] Li X Y, Law S S, Wang L X.Health monitoring of in-service bridge deck by covariance of covariance matrix of acceleration[J].Applied Mechanics and Materials, 2011, 71-78: 4808-4814.

[11] Li X Y, Wang L X,Law S S. Damage detection for structures under ambient vibration via covariance of covariance matrix and consistent regularization[J].Advances in Structural Engineering, 2013,16(1): 77-86.

[12] 岳艳芳.基于动力分析的结构损伤检测方法研究[D].南京：东南大学，2004.

[13] Allemang R J.The modal assurance criterion-twenty years of use and abuse[J].Sound and Vibration, 2003, 37(8):14-21.

Damage identification under ambient vibration based on change ratios of covariance of covariance matrix components of structural acceleration responses

WANGLi-xin1,LIXue-yan2,JIANGHui1,ZHUJia-jian1(1.CEA Key Laboratory of Earthquake Monitoring and Disaster Mitigation Technology, Earthquake Administration of Guangdong Province, Guangzhou 510070, China;2.Department of Mechanics & Civil Engineering, Jinan University, Guangzhou 510632, China)

Abstract:A new covariance of covariance (CoC) matrix is formed from the auto/cross-correlation functions of acceleration responses of a structure under ambient white noise excitation.The components of a CoC matrix are proved to be a function of modal parameters (modal frequency, mode shape and modal damping) only of the structure.Compared to the general damage-identification methods of extracting modal parameters, the formulated covariance matrix contains more information, especially the higher vibration modes of a structure.Using the change ratios of CoC matrix components, a method of damage identification is proposed for structures under ambient vibration based on vibration outputs in this paper.A seven-floor frame structure is studied through numerical simulation in two steps (namely, first damage location and then damage-extent identification) to demonstrate the efficiency of the proposed method.

Key words:damage identification; covariance of covariance matrix; ambient vibration

中图分类号:TU375.4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.022

收稿日期：2015-08-05修改稿收到日期：2015-11-01

基金项目：地震科技星火计划(XH16031);国家自然科学青年基金(51208230);广东省重大科技专项(2012A080102008);广东省地震预警与重大工程安全诊断重点实验室建设项目(2011A060901006)

第一作者 王立新 男，博士，副研究员，1976年9月生

E-mail:wlxustc@hotmail.com