惯性稳定平台不平衡扰动建模与仿真分析

李　明， 李　洁， 张延顺(北京航空航天大学 仪器科学与光电工程学院，北京　100191)



惯性稳定平台不平衡扰动建模与仿真分析

李明， 李洁， 张延顺(北京航空航天大学 仪器科学与光电工程学院，北京100191)

摘要：理想情况下，惯性稳定平台的质心会位于其旋转轴上，但是由于加工技术等条件的限制，惯性稳定平台的质心会偏离旋转轴，并且在基座角运动和摩擦等扰动作用下，惯性稳定平台会产生偏转角，偏转角的变化会引起水平和垂直方向上的不平衡力臂变化，形成不平衡扰动。为了分析不平衡扰动对平台性能的影响，在对惯性稳定平台的动力学模型进行简化的基础上，提出通过分析平台偏转角和不平衡力臂的变化规律建立不平衡扰动模型的思想方法，以所建模型为基础，对不平衡扰动的影响进行了定量分析。仿真结果表明，不平衡扰动会使平台的角度输出稳态值超过其稳定精度要求，严重影响惯性稳定平台的稳定性能。

关键词：惯性稳定平台；摩擦；动力学模型；不平衡扰动；建模

惯性稳定平台是航空遥感系统的重要组成部分，通常采用三框架结构，由外到内分别为横滚框，俯仰框和方位框。惯性稳定平台用于隔离载机的干扰角运动，抑制干扰力矩对系统的影响，从而获取高精度的遥感数据[1-2]。

影响惯性稳定平台稳定精度的因素有很多，包括不平衡扰动、基座角运动、框架耦合、摩擦等[3]。其中，不平衡扰动包含框架质心偏离旋转轴而产生的不平衡力矩[4]，以及平台质心位移而产生的不平衡力矩[5]，本文中主要考虑框架质心偏离旋转轴产生的不平衡力矩。不平衡力矩会严重影响惯性稳定平台的稳定精度, 对于不平衡扰动建模，房建成等[3]根据不平衡力矩与电机电枢电流的关系，实时估计出不平衡扰动的大小；朱华征等[4]将加速度分别投影到内、外框架，然后利用刚体绕动点转动的动量矩定理求出不平衡扰动的模型；尹秋岩等[6]取动量轮上一个微元，通过求动量轮相对卫星质心的动量矩，可得反作用飞轮的不平衡扰动；杨秀彬等[7]分析了单框架控制力矩陀螺在高速旋转过程中，由于转子的质量分布不均使得其惯量积不为零，进而产生不平衡力矩。

在前人研究的基础上，本文提出一种惯性稳定平台不平衡扰动的建模方法，该方法利用惯性稳定平台动力学模型，分析了摩擦、基座角运动等扰动作用引起的惯性稳定平台的偏转角，以及由于偏转角而产生的不平衡力臂的变化，并在此基础上建立了不平衡扰动的模型，最后通过仿真定量分析了不平衡扰动对惯性稳定平台性能的影响。

1不平衡扰动分析

不平衡扰动是指物体质心和旋转中心不重合而产生的扰动力矩，具体到惯性稳定平台上，不平衡扰动是由于惯性稳定平台框架的质心偏离旋转轴，并且在摩擦和基座角运动等内，外扰动的作用下惯性稳定平台会发生偏转，使得不平衡力臂发生变化，进而产生不平衡扰动，不平衡扰动会引起惯性稳定平台稳定精度的下降[8]，对其性能产生较大的影响。

横滚框位于惯性稳定平台的最外框，其受到的扰动影响也最为剧烈，因此本文以横滚框为例进行研究。由于平台偏转角度的变化而产生的水平和垂直方向的不平衡力臂以及由此产生的不平衡扰动可以表示为：

lx=lcos(θp)

(1)

lz=lsin(θp)

(2)

M=m(g+az)lx+maxlz

(3)

式中l为质心偏离旋转轴而产生的不平衡力臂，θp为平台偏转的角度，lx,lz分别为不平衡力臂在水平和垂直方向的分量，m为惯性稳定平台的质量，ax和az分别为作用在惯性稳定平台框架上的水平和垂直方向上的干扰加速度。综合式(1)～式(3)，不平衡力臂的变化可以归结为平台偏角θp的变化，这样平台不平衡扰动模型可以表示为：

M=m(g+az)lcos(θp)+maxlsin(θp)

(4)

从式(4)中可以看出，惯性稳定平台偏转角度θp是影响不平衡扰动的主要因素，要建立不平衡扰动的模型，分析不平衡扰动对平台性能的影响，首要的是研究平台偏转角的变化形式。

一般情况下，惯性稳定平台的载体为小飞机，在其飞行过程中，受到阵风、大气紊流等扰动因素的影响，飞行载体会发生运动，对于惯性稳定平台而言，就形成基座角运动，基座角运动的作用形式是多种多样的，在本文的分析中将其看作典型正弦形式的干扰，表达形式为：ωb=Asin(ωt)，惯性稳定平台还存在摩擦、耦合力矩、陀螺漂移等的影响。根据文献[5]和文献[9]，框架间耦合力矩和陀螺漂移等干扰相对于摩擦和基座角运动，对惯性稳定平台的性能影响较小，故本文中忽略框架间耦合力矩和陀螺漂移等因素的影响，参照文献[9]中的惯性稳定平台动力学模型，在忽略框架之间耦合作用的情况下，可以得到基座角运动和摩擦作用下惯性稳定平台的动力学方程如式(5)所示：

(5)

式中J为平台的转动惯量，ωb为基座运动角速度，Mf为摩擦力矩。从式(5)中可以看出，在基座角运动和摩擦作用下，惯性稳定平台会产生偏转角度θp，该偏转角可以利用式(5)求出，将求得的θp代入式(4)，即可得到惯性稳定平台的不平衡扰动。

2不平衡扰动建模

由惯性稳定平台的不平衡扰动表达式(4)可以看出，要建立不平衡扰动模型，就要根据式(5)求出摩擦和基座角运动作用下平台的偏转角θp。

2.1惯性稳定平台摩擦模型

要研究摩擦和基座角运动作用下平台产生偏转角的大小，进而完成不平衡扰动建模，首先需要选择摩擦模型。一个合适的摩擦模型能够更好地描述惯性稳定平台的摩擦作用，而高精度是惯性稳定平台的重要指标，所以摩擦模型要尽可能完全地描述惯性稳定平台的摩擦现象。

Stribeck模型可以描述惯性稳定平台系统中存在的静摩擦、动摩擦，平台在低速运动时随着运动速度增大而减小的特性[10]，所以本文中选择了Stribeck摩擦模型，其关系式如(6)所示。

(6)

式中，Mc为库伦摩擦力矩，Ms为最大静摩擦力矩，ω为接触面之间的相对角速度，σ为黏性摩擦因数，ωs为Stribeck速度。式(6)综合考虑了静摩擦，库伦摩擦，黏滞摩擦和低速时的Stribeck效应，能较好的描述平台的摩擦现象，因此本文中采用式(6)所示摩擦模型，相对速度ω与摩擦力矩之间的关系如图1所示。

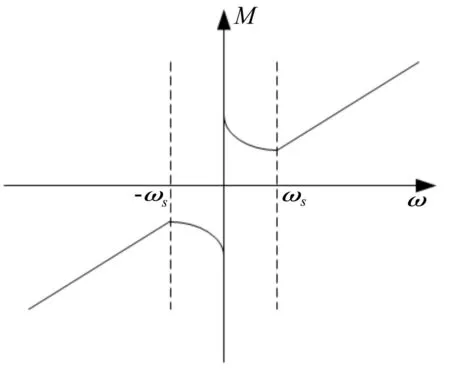
图1　摩擦模型Fig.1 Model of friction

在摩擦和基座角运动的作用下，惯性稳定平台会发生偏转，将建立的摩擦模型代入式(5)，即可求出摩擦和基座角运动作用下惯性稳定平台偏转的角度，进而实现不平衡扰动的建模。

2.2不平衡扰动建模

将Stribeck模型代入惯性稳定平台动力学模型中，相对角速度ωr即等于惯性稳定平台角速度ωp与支撑惯性稳定平台的基座角速度ωb之差。

ωr=ωp-ωb

(7)

从图1中可以看出，当惯性稳定平台相对速度ω取值不同时，相应的摩擦力矩也不相同，且速度正向和反向时的库伦摩擦力矩，最大静摩擦力矩可以看作相等，即Mss=Mns,Msc=Mnc,Msc和Mnc分别为角速度正向和反向时的库伦摩擦力矩，Mss和Mns分别为角速度正向和反向时的最大静摩擦力矩。根据图1中相对速度与摩擦力矩的关系，对ω的取值进行分类。

(1)ωp-ωb>ωs时，摩擦力矩为：

Mf=Msc+σ(ωp1-ωb-ωs)

(8)

将式(8)代入式(5)中，可得惯性稳定平台动力学方程为：

对上述方程进行积分(初始条件为0)，可得ωp-ωb>ωs时，惯性稳定平台偏转角θp1的表达式：

(9)

将式(9)代入式(4)，可得ωp-ωb>ωs时，惯性稳定平台不平衡扰动的表达式：

M=m(g+az)lcos(θp1)+maxlsin(θp1)

(10)

(2)ωb-ωp>ωs时，摩擦力矩为：

Mf=-Mnc-σ(ωb-ωp2-ωs)

(11)

将式(11)代入式(5)，可得惯性稳定平台动力学方程为：

同样，对上述方程进行积分运算，得到在ωb-ωp>ωs时惯性稳定平台偏转角θp2的表达式：

(12)

将式(12)代入式(4)，可得ωb-ωp>ωs时，惯性稳定平台的不平衡扰动：

M=m(g+az)lcos(θp2)+maxlsin(θp2)

(13)

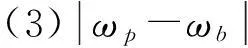
①ωp=ωb，即相对速度为0时，惯性稳定平台摩擦力矩为：

(14)

将式(14)代入式(5)，可得惯性稳定平台的动力学方程：

对应得到惯性稳定平台偏转角θp3的表达式为：

(15)

将式(15)代入式(4)，可得对应情况下的不平衡扰动：

M=m(g+az)lcos(θp3)+maxlsin(θp3)

(16)

②ωp>ωb时，惯性稳定平台摩擦力矩为：

(17)

将式(17)代入到式(5)，可得惯性稳定平台动力学方程为：

这种情况下，惯性稳定平台偏转角θp4可以表示为：

θp4=

(18)

式中：

将式(18)代入到式(4)，可得对应情况下的不平衡扰动：

M=m(g+az)lcos(θp4)+maxlsin(θp4)

(19)

③ωp<ωb时，惯性稳定平台摩擦力矩为：

(20)

将式(20)代入式(5)中，可得此时惯性稳定平台动力学方程为：

惯性稳定平台偏转角θp5可以表示为：

(21)

式中：

将式(21)代入式(4)，可得相应情况下的不平衡扰动：

(22)

式(9)、式(12)、式(15)、式(18)和式(21)为基座角运动和摩擦作用下，惯性稳定平台偏转的角度；式(10)、式(13)、式(16)、式(19)和式(22)为对应情况下的不平衡扰动模型。在角速度ωb的幅值和频率分别取不同值的情况下，惯性稳定平台摩擦作用的影响也不同，进而导致由摩擦和基座角运动形成的惯性稳定平台偏转角也有差异。不平衡扰动受惯性稳定平台自身参数(m,l,J)、干扰加速度(ax,az)、摩擦参数(Mnc,Mns,Msc,Mss,ωs)以及基座角运动幅值A和频率ω等因素的影响。这里，m,l,J,Mnc,Mns,Msc,Mss,ωs的值根据先验知识可以得到，ax,az为惯性稳定平台受到水平和垂直方向的干扰加速度，A和ω可以看作不平衡扰动模型的输入幅值和频率，利用建立的不平衡扰动的模型，即可分析不平衡扰动对惯性稳定平台性能的影响。

3不平衡扰动影响分析

实际上，惯性稳定平台控制系统通常采用三环控制方法，由电流环、稳定回路和跟踪回路组成，控制系统采用经典PID控制方法，能够使惯性稳定平台按照要求保持惯性稳定，并能够跟踪当地地理水平。在上述基础上，将建立的不平衡扰动模型加入控制系统中，利用SIMULINK仿真软件即可分析不平衡扰动对惯性稳定平台性能的影响。不平衡扰动作用下，惯性稳定平台控制系统见图2。

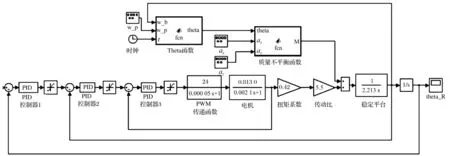
图2　包含不平衡扰动的惯性稳定平台控制系统Fig.2 Control system of inertially stabilized platform including unbalanced disturbance

上述控制系统模型中，惯性稳定平台参数为m=120 kg，l=5 mm，J=2.213 kg·m2。摩擦参数为M-sc=2 N·m,M-ss=6.25 N·m,M-nc=2 N·m,M-ns=6.25 N·m,ωs=0.01 rad/s，a=0.02 N·m/(rad/s)。因为基座角运动可以看作典型正弦作用，可以将其表示为ωb=Asin2πft。惯性稳定平台基座角运动幅值最大值为100°/s，这里按照惯性稳定平台运动的剧烈情况分别取5°/s,80°/s两种情况；由于惯性稳定平台带宽较窄，扰动频率分别取0.5 Hz,1.5 Hz。干扰加速度最大值为±1 g，用随机函数代替，当其幅值分别取±0.2 g,±0.6 g,±1 g时，在不平衡扰动作用下，惯性稳定平台角度如图3～图5所示，图片右上角为稳态放大图。

图3　干扰加速度幅值为±0.2 g时，在不平衡扰动作用下，惯性稳定平台角度输出Fig.3 Angle output of inertially stabilized platform under the function of unbalanced disturbance, when the amplitude of acceleration is ±0.2 g

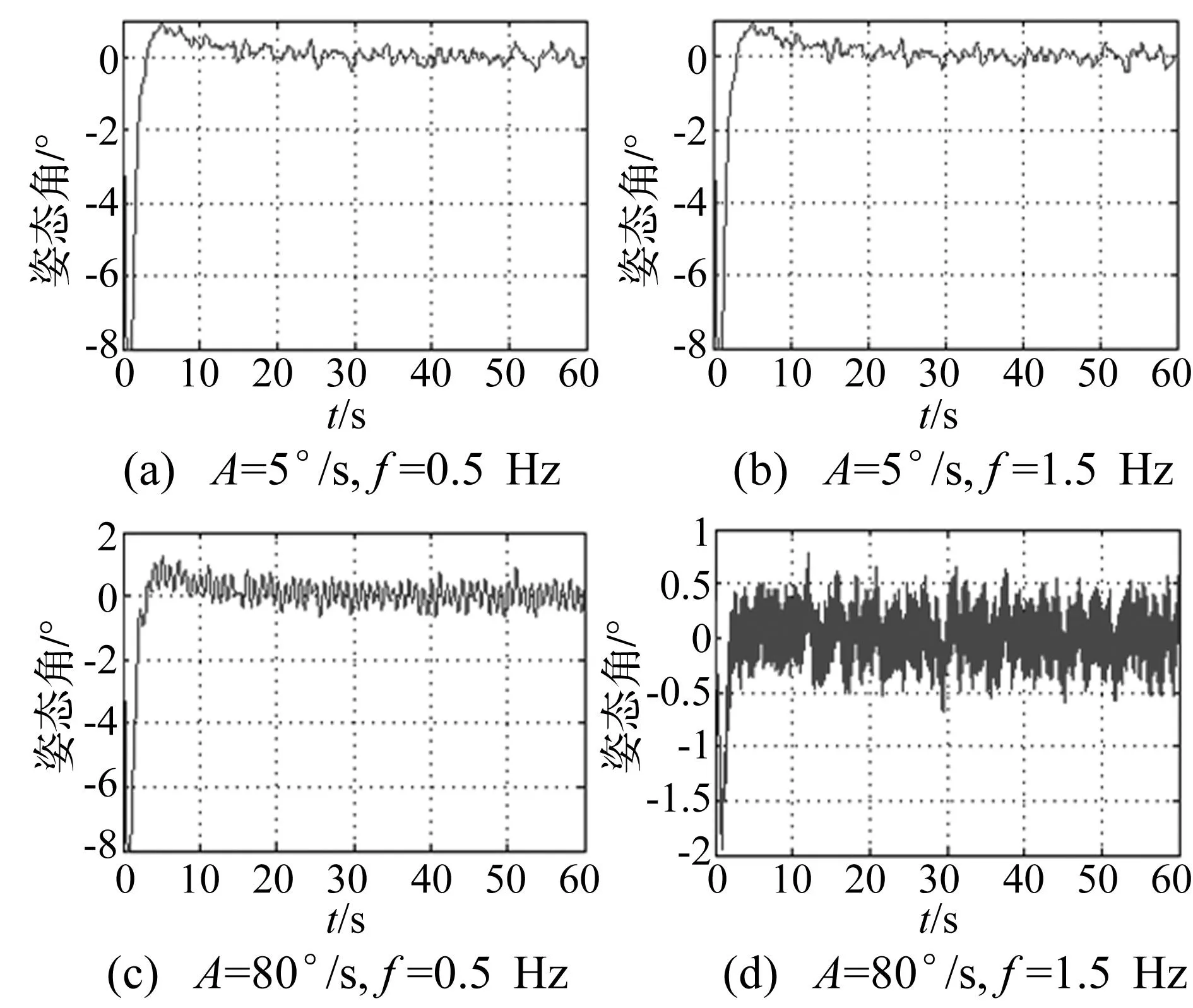
图4　干扰加速度幅值为±0.6 g时，在不平衡扰动作用下，惯性稳定平台角度输出Fig.4 Angle output of inertially stabilized platform under the function of unbalanced disturbance, when the amplitude of acceleration is ±0.6 g

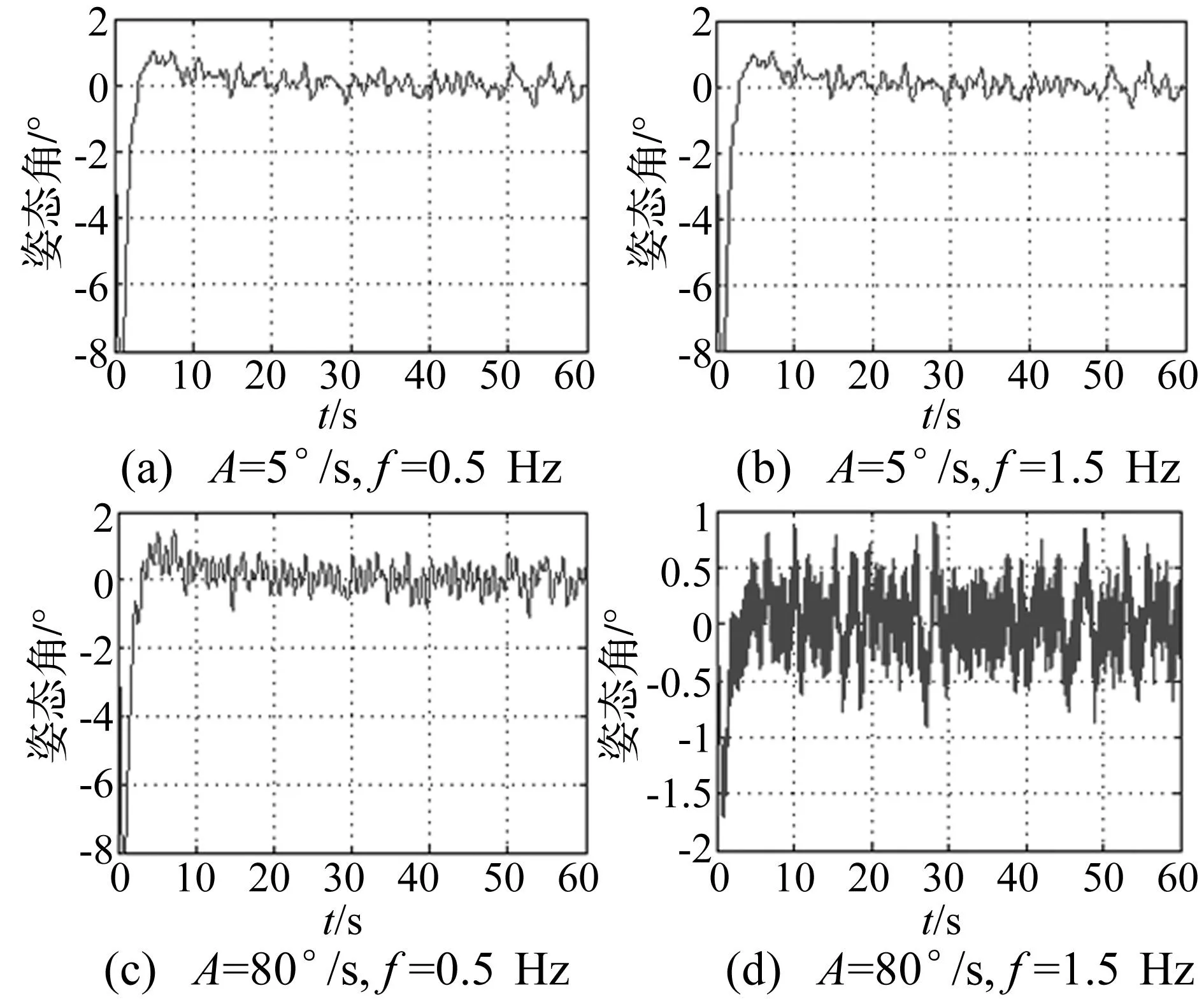
图5　干扰加速度幅值为±1 g时，在不平衡扰动作用下，惯性稳定平台角度输出Fig.5 Angle output of inertially stabilized platform under the function of unbalanced disturbance, when the amplitude of accelerationis ±1 g

从图3～图5中可以看出，在不同的输入幅值，频率以及干扰加速度条件下，不平衡扰动引起的惯性稳定平台的运动，经过短暂的过渡过程后进入稳态。当干扰加速度幅值为±0.2 g,±0.6 g,±1 g时，在给定的幅值和频率变化范围内，系统的稳态值分别达到0.5°,0.6°,0.8°，大大超过了惯性稳定平台0.2°的精度要求，惯性稳定平台的性能会受到较大的影响。可见，不同情况下，由基座角运动、摩擦和干扰加速度引起的不平衡扰动作用，对惯性稳定平台的稳定精度具有影响，需要克服其产生的误差。

4结论

本文通过对惯性稳定平台动力学模型的分析，得出不平衡扰动与惯性稳定平台基座角运动和摩擦等其他扰动因素有关的结论，并在此基础上，通过对摩擦模型的分析，在求出摩擦和基座角运动作用下平台偏转角和不平衡力臂的变化规律的情况下，建立了惯性稳定平台的不平衡扰动模型。

最后对不平衡扰动作用下，惯性稳定平台角度输出进行了定量分析，结果表明，在不平衡力矩作用下，惯性稳定平台的角度输出稳态值最大可以达到0.8°，大大超过了系统的精度要求。可见不平衡扰动会对惯性稳定平台产生较大的影响，对其进行建模研究，分析其产生机理具有重要的意义。

参 考 文 献

[ 1 ] Hilkert J M. Inertially stabilized platform technology: concepts and principles[J]. IEEE Control Systems Magazine, 2008(12): 26-46.

[ 2 ] Masten M K. Inertially stabilized platform for optical imaging system: tracking dynamic targets with mobile sensors[J]. IEEE Systems Magazine, 2008(12): 47-64.

[ 3 ] 房建成, 戚自辉, 钟麦英. 航空遥感用三轴遥感平台不平衡力矩前馈补偿方法[J]. 中国惯性技术学报,2010,18(1):38-43.

FANG Jian-cheng,QI Zi-hui,ZHONG Mai-ying. Feedforward compensation method for three axes inertially stabilized platform imbalance torque[J]. Journal of Chinese Inertial Technology,2010, 18(1): 38-43.

[ 4 ] 朱华征, 范大鹏, 张文博,等. 质量不平衡力矩对导引头伺服机构性能影响分析[J]. 红外与激光工程,2009,38(5):767-772.

ZHU Hua-zheng, FAN Da-peng, ZHANG Wen-bo,et al. Influence analysis of the mass imbalance torque on the performance of seeker servo mechanism[J]. Infrared and Laser Engineering, 2009,38(5): 767-772.

[ 5 ] 王祖温, 李延斌, 包钢. 3自由度气浮台力学性能研究-关于自重作用下不平衡力矩的分析[J]. 机械工程学报, 2006,42(4): 179-184.

WANG Zu-wen, LI Yan-bin, BAO Gang. Study on the mechanics property of three degrees of freedom air-bearing testbed-analysis on unbalance torque acted on gravity[J]. Journal of Mechanical Engineering,2006,42(4):179-184.

[ 6 ] 尹秋岩，赵健康，戴金海. 反作用飞轮内干扰抑制方法研究[J]. 电子与信息学报，2007,29(6)：1521-1524.

YIN Qiu-yan, ZHAO Jian-kang, DAI Jin-hai. A method of control inner disturb to the reaction wheel[J]. Journal of Electronics & Information Technology,2007,29(6)：1521-1524.

[ 7 ] 杨秀彬，常琳，金光. 单框架控制力矩陀螺转子动不平衡对遥感卫星成像的影响[J].中国光学，2012,5(4)：358-365.

YANG Xiu-bin, CHANG Lin, JIN Guang. Influence of dynamic imbalance of SGCMG rotor on remote sensing satellite imaging[J]. Chinese Optics,2012,5(4)：358-365.

[ 8 ] Li B, Hullender D, Direnzo M. Nonlinear induced disturbance rejection in inertial stabilization system[J]. IEEE Control Systems Technology, 1998, 6(3): 421-427.

[ 9 ] 阴蕊, 房建成, 钟麦英. 航空遥感用三轴遥感平台动力学建模与仿真[J]. 中国惯性技术学报,2011,19(6):676-680.

YIN Rui, FANG Jian-cheng, ZHONG Mai-ying. Dynamic modeling and simulation of remote sensing platform for aerial remote sensing system[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 676-680.

[10] 朱如意，丁祝顺，蒋鸿翔. 遥感平台摩擦力矩的非线性校正补偿方法[J]. 导航与控制, 2011,10(4): 21-25.

ZHU Ru-yi, DING Zhu-shun, JIANG Hong-xiang. Method of friction compensation based on nonlinear revision in remote sensing platforms[J]. Navigation and Control, 2011,10(3):21-25.

Modeling and simulation of imbalance disturbance for inertially stabilized platforms

LIMing,LIJie,ZHANGYan-shun(School of Instrument Science and Opto-electronics Engineering, Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Abstract:Ideally, the centroid of an inertially stabilized platform is located on the axis of rotation, but in fact, the centroid of an inertially stabilized platform will deviate from the axis of rotation because of the limits of processing technology.What’s more, under the function of base angle movement and friction, an inertially stabilized platform will produce a deflecting angle.A change of deflecting angle will cause a horizontal and vertical change of the arm of force; in this case, an imbalance disturbance comes into being.In order to analyze the influence of the imbalance disturbance, the paper takes the simplified dynamical model of an inertially stabilized platform as its basis and introduces the idea of establishing unbalanced disturbance by analyzing the changing rule of the deflecting angle and the arm of force.Based on the unbalanced disturbance, it analyzes the effect of an unbalanced disturbance on an inertially stabilized platform by quantitative simulation.The results show that the output angle of an inertially stabilized platform in a stabilized state exceeds the stabilized demand under the function of unbalanced disturbance.

Key words:inertially stabilized platform; friction; dynamical model; imbalance disturbance; modeling

中图分类号:U666.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.021

收稿日期：2014-08-20修改稿收到日期：2015-04-17

基金项目：国家自然科学基金(11202010)

第一作者 李明 女，讲师，1978年生

E-mail:liliyalm@buaa.edu.cn