EMD降噪在高速铁路路基沉降预测中的应用

周　俊， 马建林， 徐　华， 黄小福(西南交通大学 土木工程学院，成都　610031)



EMD降噪在高速铁路路基沉降预测中的应用

周俊， 马建林， 徐华， 黄小福(西南交通大学 土木工程学院，成都610031)

摘要：高速铁路路基实测沉降曲线通常含有噪声，不宜直接进行曲线拟合。将EMD降噪法引入到沉降预测中，首先对路基沉降观测数据进行滤波降噪，然后将降噪后的沉降曲线作为原始数据进行曲线拟合。结合数学模拟实验和京沪高速铁路典型路基沉降板观测数据，分析了EMD降噪效果和降噪后的沉降预测结果。分析结果表明，EMD降噪很好地消除了混杂在实测沉降曲线中的随机误差和异常的波动成分；降噪后的沉降速率曲线更为平缓，能直观地反映出沉降趋于稳定的时间和过程；降噪后的曲线拟合相关系数高，误差平方和小，沉降预测精确度得到了显著提高且能够满足评估指南的要求。

关键词：沉降预测；EMD降噪；相关系数；高速铁路

高速铁路客运专线要实现快速、舒适和安全，必须保证线路的平顺和稳定，这就要求必须严格控制线下结构物的沉降变形，尤其是工后沉降量。而设计还无法准确预估沉降变形和有效地控制工后沉降，用土工试验按常规的一维固结理论进行沉降计算是常用的方法，但地基沉降属于三维课题且实际情况又很复杂，其结果往往与实测结果相距甚远，因此利用沉降观测资料采用曲线拟合的方法预测后期沉降和最终沉降有着重要的现实意义[1-4]。

在高速铁路沉降监测数据采集过程中，由于受到施工及测量误差等的影响，实测沉降曲线会不可避免地含有一定程度的噪声[5]。因此，在进行曲线拟合之前，最好将混杂在沉降观测资料中的噪声去除或减少，以提高沉降预测精确度。文献[4]将小波降噪应用于高速铁路的沉降预测，文献[5-6]在软土地基沉降预测中应用了小波降噪分析，均收得了良好的降噪效果。但是小波降噪的缺陷在于，对于不同的信号需要选择合适的基函数和分解层数[7-8]，并且小波窗内的信号必须满足平稳性。相比于小波降噪，EMD降噪法具有自适应性，表现在基函数自动产生、自适应的滤波特性和自适应的多分辨率，并且能对非线性、非平稳信号进行有效分析[8-10]。因此，采用EMD降噪法对沉降曲线进行滤波降噪是一种合适且正确的选择。

本文将EMD降噪法引入到沉降预测中，首先采用数学模拟实验分析EMD降噪对模拟沉降曲线的降噪处理效果，然后对京沪高速铁路(京徐段)路基实测沉降曲线进行滤波降噪，消除其异常的波动成分，最后对降噪后的曲线进行沉降预测并分析其预测结果，从而探讨EMD降噪在高速铁路路基沉降预测中的适应性。

1EMD降噪滤波原理

1.1HHT和EMD简介

Hilbert-Huang Transform(HHT)由Huang[9]提出并发展，是一种比傅里叶变换及小波变换更具适应性的时频分析方法。EMD是HHT的核心，也称为筛选过程，可以将原始信号X分解为n个IMF分量和一个余项R的和，即

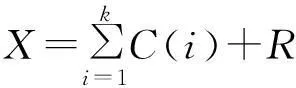
(1)

EMD的分解过程详见文献[9]，本文不再赘述。EMD依据数据自身的时间尺度特征来进行信号分解，无须预先设定任何基函数。这一点与建立在先验性的谐波基函数和小波基函数上的傅里叶分解与小波分解方法具有本质性的差别。正是由于这样的特点，EMD方法在理论上可以应用于任何类型的信号的分解，因而在处理非平稳及非线性数据上， 具有非常明显的优势。

1.2EMD降噪

Wu等[11]经过大量的实验，研究了白噪声经EMD分解后各个IMF分量的特性，发现除第一个IMF分量外，① 各个IMF分量的概率密度函数近似服从正态分布；② 各个IMF分量的能量密度与其平均周期的乘积为一个常量，即

(2a)

(2b)

(2c)

因此，基于白噪声各个IMF分量的特性，可以建立适当标准，在信号重构时，将与噪声相对应的IMF分量去除，就可实现降噪的目的[12-13]。通常噪声与有用信号具有不同的频谱特征，随机噪声主要包含于低阶IMF分量中，若前k-1阶IMF被判断主要成分为噪声，则将其全部去除，EMD降噪结果为：

(3)

由式(3)可以看出，EMD降噪的关键在于噪声与有效信号界限k值的确定。文献[14]指出，在实际应用中，可以选取式(4)作为k值的确定标准

(4)

由于EMD法具有自适应性、完备性和正交性[9]，这种基于IMF分量的低通滤波器可以充分保留信号本身的非平稳非线性特征，同时减少或消除了信号中混杂的噪声。基于EMD的降噪滤波方法已在GPS多路径效应[14]、煤冲击破坏SHPB测试信号[15]、滚动轴承早期故障诊断[16]、大型旋转机械非平稳振动信号[17]等方面得到了较好的应用。

2沉降观测数据分析

2.1路基沉降变形的特点

高速铁路路基段观测标志有三种，沉降板、单点沉降计和表层观测桩。因沉降板布置时间最早，观测时间最长，故更能反映路基沉降的发展过程。京沪高速铁路(京徐段)共埋设沉降板2 770处，沉降监测时间范围为2008年10月～2010年4月，沉降板累计沉降分布范围见图1。

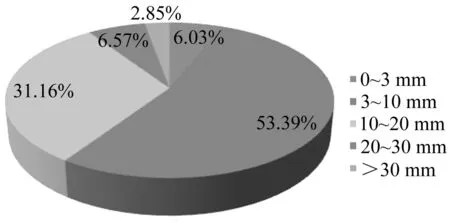
图1　沉降板实测总沉降分布范围Fig.1 Distribution of cumulative subgrade settlement measured by settlement plates

由图1可知，沉降板累计沉降量大于30 mm的测点仅占沉降板总数2.85%。总体来看路基累计沉降量较小。通常路基填筑完成1个月后，沉降迅速由快速发展阶段转换为稳定收敛阶段，后期的沉降变形量相对较小，由于受到施工及测量误差等的影响，实测沉降曲线会不可避免地含有一定程度的噪声[5]，一般呈现出“小量级、大波动”的特点，是一种非线性、非平稳信号。

2.2沉降预测对观测数据的需求

为了准确有效地进行高速铁路路基沉降预测，对观测数据在观测时间频次和观测质量两个方面有以下需求：

(1)根据评估指南[1]的要求，路基填筑完成或施加预压荷载后应有不少于6个月的观测和调整期，沉降观测频次要求详见评估指南中表4.2.7，最终沉降的预测时间应满足以下条件：

St/S∞≥75%

(5)

式中，St为预测时的沉降观测值，S∞为预测的最终沉降值。沉降和时间以路基填筑完成或堆载预压后为起始点。

(2) 观测数据真实可靠，严格控制测量误差，若沉降曲线出现异常或施工环境发生变化时，应立即采取措施。《京沪高速铁路线下工程沉降变形观测及评估实施细则》[18]规定，当两次连续观测的沉降差值大于4 mm时应加密观测频次；当出现沉降突变、地下水变化及降雨等外部环境变化时应增加观测频次；当路基填筑过程中心地基处沉降观测点沉降量大于10 mm/天，应停止填筑施工，待沉降稳定后再恢复填土，必要时采用卸载措施。

观测数据的准确性必然影响沉降预测精度，而观测数据中一般都含有测量误差。为了提高沉降预测的精确度，应首先对沉降曲线进行滤波降噪，消除或减少由于测量误差等带来的影响。由于高速铁路路基实测沉降曲线是一种具有“小量级、大波动”特点的非线性、非平稳信号，而EMD法能够很好地消除混杂在非线性、非平稳信号中的噪声。因此，本文将采用EMD法对沉降曲线进行滤波降噪。

3EMD降噪数学实验

3.1模拟沉降曲线

高速铁路路基实测沉降曲线不可避免地存在噪声，而我们却无法获知其完全不含噪声的形状。为了直观地、定量地评价降噪效果，首先采用数学方法模拟出一条理想沉降曲线，然后加入预设的噪声构成模拟沉降曲线。采用EMD降噪法对模拟沉降曲线进行滤波降噪并评价其降噪效果，若降噪效果良好，则可以将EMD降噪应用于实测沉降曲线，并进行沉降预测。

根据太沙基一维固结理论，地基沉降随时间的发展符合指数曲线趋势，这一结论也在大量的工程实例得到了验证。因此，为了模拟高速铁路路基实际沉降过程，本实验选取满足式(6a)的一组数据作为本实验模拟的不含噪声的理想沉降曲线，式(6b)作为本实验包含噪声的模拟沉降曲线，两条沉降曲线如图2所示。

(6a)

s=x+e

(6b)

e=σ×N(0,1)

(6c)

式中，x为理想信号，s为含噪信号，t为模拟时间，σ为噪声强度，e为噪声。沉降观测误差通常都是偶然误差，总体上呈现出一定的规律性，是符合正态分布的随机变量，也可以称作是白噪声。本实验用于产生随机噪声的正态分布选取为N(0，1)。高速铁路沉降观测采用二等水准测量，沉降变形的观测精度为±1 mm。因此，本实验噪声强度取为σ=1 mm。值得说明的是，高速铁路对沉降观测的频率及统计的要求较高，粗差在数据录入时已经处理，故本项误差不在本实验的考虑之列[1]。

图2　理想沉降曲线与模拟沉降曲线Fig.2 Ideal settlement and simulative settlement

3.2试验结果评价准则

对降噪效果的评价标准[7, 14]为信噪比SNR和均方误差MES。

(7)

(8)

式中，x为不含噪声的理想信号，s为滤波降噪后的信号。信噪比SNR越高，表明信号中残留的噪声越小，信噪比的单位是分贝(dB)。均方误差MES越小，表示降噪效果越好。

3.3试验结果与分析

对图2中的模拟沉降曲线进行EMD分解，得到7个IMF分量C1～C7和1个残余量R，如图3所示。按照式(4)给出的k值确定标准，k值与Rk的关系如图4所示。当k=5时，Rk>C，C1～C4可判定为噪声部分，C5～C7和R为有效信号部分。

图3　各个IMF分量及残余量(纵坐标单位：mm)Fig.3 Seven IMF components and a residual amount (ordinate unit: mm)

图4　k值与Rk的关系Fig.4 Relationship between k and Rk

为了验证式(4)确定标准的准确性，采用统计分析软件SPSS对C2～C7进行了正态性检验。SPSS中规定，对于无权重或整数权重，在加权样本大小位于3 和 5 000之间时，正态性检验采用非参数检验方法Shapiro-Wilk检验(W 检验)。在表1中，C2～C4的P值均大于0.05；在图6中，C2～C4的直方图与正态分布曲线吻合良好，表明C2～C4近似服从正态分布。根据Wu等[11]的实验结论，白噪声经EMD分解后除第一个IMF分量外，各个IMF分量的概率密度函数近似服从正态分布。而频率最高的第一阶IMF分量C1几乎全部是噪声可直接去除，C2～C4符合作为白噪声IMF分量的特征，由此也验证了式(4)k值确定标准的准确性。

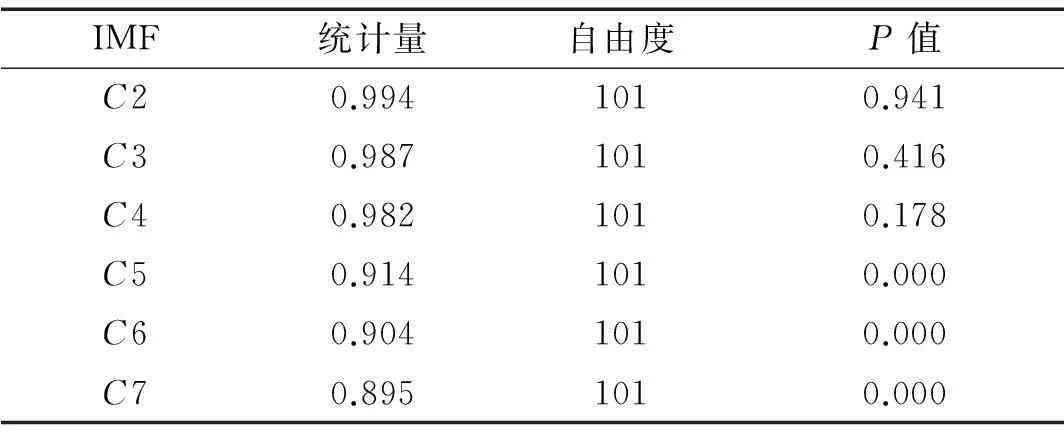
表1　正态性检验结果(Shapiro-Wilk 检验)

重构C5～C7和R即可得到降噪后的沉降曲线，如图5所示，EMD降噪很好地消除了添加在模拟沉降曲线中的噪声，并且降噪后沉降曲线与不含噪声的理想沉降曲线吻合较好。表2给出了模拟沉降曲线采用EMD的降噪结果，信噪比SNR得到了显著提高，均方误差MES也明显减小。综上所述，EMD降噪对模拟沉降曲线的降噪效果非常好，可以将其应用于高速铁路路基的沉降预测。

图5　降噪后沉降曲线与模拟沉降曲线、理想沉降曲线对比Fig.5 Comparison among simulative settlement,filtered settlement and ideal settlement

沉降曲线类别SNR/dBMES/mm2模拟沉降曲线24.4241.134降噪后沉降曲线31.7860.208

4EMD在沉降预测中的应用

4.1沉降曲线降噪

前文中的数学实验验证了EMD降噪对于模拟沉降曲线具有良好的降噪效果，因此可以将EMD降噪运用于高速铁路路基沉降预测中，并通过工程实例考察其对于提高沉降预测精确度的表现。

以京沪高速铁路(京徐段)3个典型路基沉降板观测点为例，3条沉降曲线分别处于不同的量级，其原始沉降曲线和降噪后沉降曲线如图7所示。由图7(a)～图7(c)可知，EMD降噪很好地消除了混杂在典型路基沉降板观测数据中的随机误差和异常的波动成分。

沉降的发展是一个随时间推移逐渐趋于稳定的过程，因此在沉降稳定或接近稳定的时候，沉降速率会明显地在零值附近稳定[4]。图8(a)～图8(c)给出了3个路基测点原始和降噪后沉降速率曲线的对比图，原始沉降速率曲线在观测后期仍具有较大的波动性，无法明确判断沉降是否趋于稳定。而降噪后的沉降速率曲线较为平缓，尤其是在图8(a)～图8(c)中，可以直观地反映出路基1和路基3沉降趋于稳定的时间和过程，也从侧面验证了EMD对于沉降曲线良好的降噪效果。

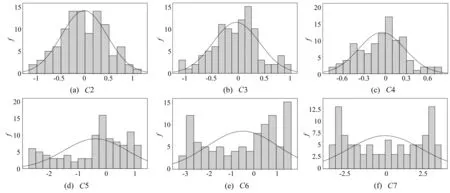
图6　C2～C7直方图Fig.6 Histograms of C2-C7

图7　典型路基原始沉降曲线和降噪后沉降曲线Fig.7 Three typical subgrade settlement curves and their filtered curves

图8　原始沉降速率与滤波后沉降速率对比Fig.8 Comparison of settlement rate between original and filtered curves

4.2双曲线法

双曲线法认为累计沉降量与时间符合双曲线递减的规律，其基本方程如下：

(9)

式中：S0为拟合起点的累计沉降量；St为t时刻的累计沉降量；α,β为待定参数。

将式(9)改写为如下的形式：

(10)

由式(10)和图9可以看出，α和β分别为(t-t0)/(St-S0)～(t-t0)关系图中的截距和斜率，据此可以用线性回归方程求出待定参数α和β，具体计算方法如下：

(11)

(2) 将得到的α、β和S0、t0代入式(9)，则可以求解任意时刻t的预测沉降量St，而最终沉降量S∞则可用下式求得：

S∞=S0+1/β

(12)

图9　双曲线法的拟合直线Fig.9 Filtered straight line of hyperbolic method

4.3沉降预测效果评价

采用双曲线法，以路基填筑完成时间为拟合起点对原始沉降曲线和降噪后沉降曲线进行沉降预测，其曲线拟合相关系数、误差平方和详见表3，其沉降预测曲线见图10(a)～10(c)。为了更加直观地评价沉降预测效果，使用前期数据对实测的最后30天观测数据做出预测，将预测值与实测数据进行对比分析，详见表4。

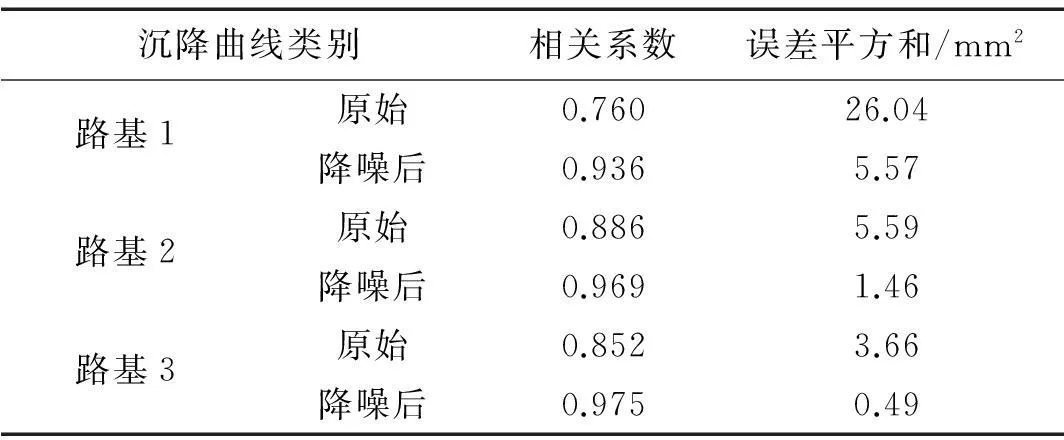
表3　原始沉降曲线与降噪后沉降曲线预测结果对比

由表3、表4和图10(a)～图10(c)可以得出以下结论：

(1) 由表3可知，直接采用原始沉降曲线进行沉降预测时，拟合相关系数小于0.92，误差平方和较大，无法满足评估指南[1]的要求。

(2) 在表3中，采用降噪后沉降曲线进行沉降预测时，拟合相关系数高，误差平方和明显减小，图10中的预测曲线与降噪后沉降曲线吻合较好，沉降预测曲线趋势稳定。

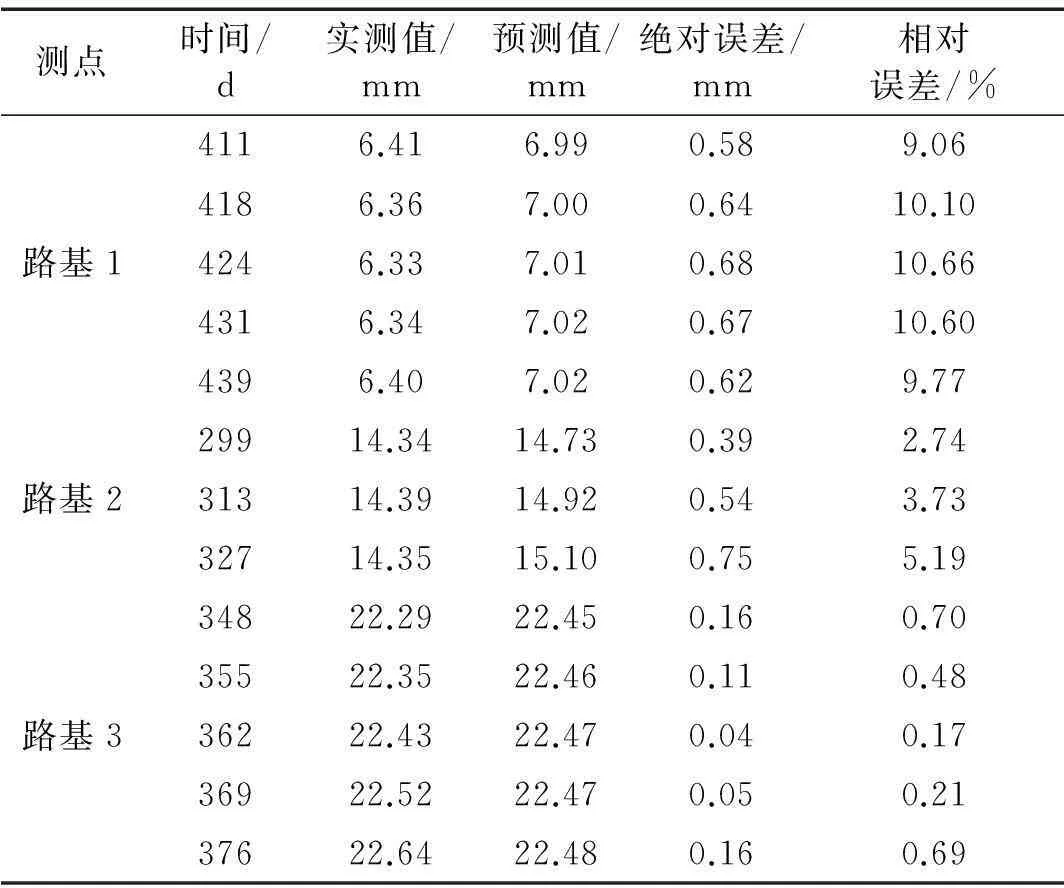
表4　最后30天的沉降预测值及误差

图10　降噪后沉降预测曲线Fig.10 Filtered curves and their prediction curves

(3) 由表4可知，3个路基测点最后30天的沉降预测值与实际值比较接近，其绝对误差和相对误差均较小。

由此可以看出，EMD降噪显著地提高了沉降预测的精确度，可以在高速铁路路基沉降评估中加以应用。

5结论

(1) 由于受到施工及测量误差等的影响，高速铁路路基实测沉降曲线会不可避免地含有一定程度的噪声，一般呈现出“小量级、大波动”的特点，并且是一种非线性、非平稳的信号。

(2) EMD降噪对高速铁路路基沉降曲线的降噪处理效果非常好，很好地消除了随机误差和异常的波动成分。

(3) 典型路基沉降板实测沉降曲线经EMD降噪后，曲线拟合相关系数高，误差平方和小，沉降预测曲线趋势稳定，沉降预测精确度得到了显著提高且能够满足评估指南的要求。

(4) EMD降噪技术应用于沉降预测的关键点在于噪声与有效信号界限k值的确定，通过数学实验表明，文献[14]中的确定标准是准确可行的。

(5) 本文将EMD降噪引入到京沪高速铁路路基的沉降预测中，为沉降评估提供了一种新的思路，但是EMD降噪对于桥梁、涵洞和隧道等结构物以及其他客运专线的适用性尚需进一步验证。

参 考 文 献

[ 1 ] 中华人民共和国铁道部.铁建设[2006] 158号 客运专线铁路无碴轨道铺设条件评估技术指南[S].北京: 中国铁道出版社, 2006.

[ 2 ] 中华人民共和国铁道部.铁建设函[2005] 754号 客运专线无砟轨道铁路设计指南[S].北京: 中国铁道出版社, 2005.

[ 3 ] 潘林有, 谢新宇.用曲线拟合的方法预测软土地基沉降[J].岩土力学, 2004, 25(7): 1053-1058.

PAN Lin-you, XIE Xin-yu.Observational settlement prediction by curve fitting methods[J].Rock and Soil Mechanics, 2004, 25(7): 1053-1058.

[ 4 ] 胡伟明.基于小波和时间序列分析的高速铁路沉降预测方法研究[D].成都：西南交通大学, 2011.

[ 5 ] 汪莹鹤, 王保田.基于小波降噪与最小二乘支持向量机的公路软基沉降预测模型[J].公路交通科技,2008,25(6):40-43.

WANG Ying-he, WANG Bao-tian.A settlement prediction model for soft foundations based on wavelet de-noising and LSSVM[J].Journal of Highway and Transportation and Development, 2008,25(6): 40-43.

[ 6 ] 易富, 朱尧, 金艳, 等.灰色模型预测软土地基沉降的小波降噪分析[J].公路交通科技, 2014, 31(2): 21-26.

YI Fu, ZHU Yao, JIN Yan,et al.Analysis of wavelet denoising for predicting soft soil foundation settlement with grey model[J].Journal of Highway and Transportation and Development, 2014, 31(2): 21-26.

[ 7 ] 陈仁祥, 汤宝平, 马婧华.基于EEMD的振动信号自适应降噪方法[J].振动与冲击, 2012, 31(15): 82-86.

CHEN Ren-xiang, TANG Bao-ping, MA Jing-hua.Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal[J].Journal of Vibration and Shock, 2012, 31(15): 82-86.

[ 8 ] 张胜.HHT理论及其在岩土工程信号分析中的应用[D].长沙：长沙理工大学, 2011.

[ 9 ] Huang N E, Zheng S, Long S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].The Royal Society, 1998, 454: 903-995.

[10] 赵志宏, 杨绍普, 申永军.一种改进的EMD降噪方法[J].振动与冲击, 2009, 28(12): 35-37.

ZHAO Zhi-hong, YANG Shao-pu, SHEN Yong-jun.Improved EMD based de-noising method[J].Journal of Vibration and Shock, 2009, 28(12): 35-37.

[11] Wu Z, Huang N E.A study of the characteristics of white noise using the empirical mode decomposition method[J].The Royal Society, 2004, 460: 1597-1611.

[12] Flandrin P, Rilling G, Goncalves P.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters, 2004, 11(2): 112-114.

[13] Boudraa A, Cexus J.EMD-Based Signal Filtering[J].IEEE Transactions on Instrumentation and Measurement,2007,56(6):2196-2202.

[14] 戴吾蛟, 丁晓利, 朱建军, 等.基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J].测绘学报, 2006, 35(4): 321-327.

DAI Wu-jiao, DING Xiao-li, ZHU Jian-jun,et al.EMD filter method and its application in GPS multipath[J].Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327.

[15] 李成武, 解北京, 杨威, 等.基于HHT法的煤冲击破坏SHPB测试信号去噪[J].煤炭学报, 2012, 37(11): 1796-1802.

LI Cheng-wu, XIE Bei-jing, YANG Wei,et al.Coal impact damage SHPB testing signal de-noising based on HHT method[J].Journal of China Coal Society, 2012, 37(11): 1796-1802.

[16] 苏文胜, 王奉涛, 张志新, 等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击, 2010, 29(3): 18-21.

SU Wen-sheng, WANG Feng-tao, ZHANG Zhi-xin,et al.Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J].Journal of Vibration and Shock, 2010, 29(3): 18-21.

[17] 曹冲锋, 杨世锡, 杨将新.大型旋转机械非平稳振动信号的EEMD降噪方法[J].振动与冲击, 2009, 28(9): 33-38.CAO Chong-feng, YANG Shi-xi, YANG Jiang-xin.De-noising method for non-stationary vibration signals of large rotating machineries based on ensemble empirical mode decomposition[J].Journal of Vibration and Shock, 2009, 28(9): 33-38.

[18] 京沪高速铁路股份有限公司.京沪高速铁路线下工程沉降变形观测及评估实施细则[G].2008.

Application of EMD denoising method in subgrade settlement prediction of high-speed railways

ZHOUJun,MAJian-lin,XUHua,HUANGXiao-fu(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Abstract:In the presence of noise, most measured subgrade settlement curves of high-speed railways are not suitable for predicting settlement directly.In this paper, measured settlement curves of subgrades were filtered by EMD denoising method.Then, the filtered settlement curves were used to predict settlement.By combining mathematical experiments and measured data of subgrades in the Beijing-Shanghai high-speed railway, effects of noise reduction and results of settlement prediction were analyzed.The analysis shows that random errors and abnormal fluctuation components mixed with measured settlement curves had been eliminated well through the EMD denoising method.Settlement-rate curves of filtered settlement are smoother and can directly reflect when and how settlement curves become stable.Settlement prediction accuracy has been significantly improved, with high correlation coefficients and low square errors.

Key words:settlement prediction; EMD denoising method; correlation coefficient; high-speed railway

中图分类号:TU433

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.011

通信作者马建林 男，教授， 博士生导师，1958年2月生

收稿日期：2015-01-06修改稿收到日期：2015-05-01

基金项目：铁道部高速铁路科技重大课题(2008G031-B)；国家自然科学基金(51278432)

第一作者 周俊 男，博士生，1988年7月生

E-mail:majianlin01@126.com