基于三次指数平滑的云南学龄儿童人数预测研究

彭乃驰， 党　婷

(云南大学 旅游文化学院信科系，云南 丽江 674199)



基于三次指数平滑的云南学龄儿童人数预测研究

彭乃驰， 党婷

(云南大学 旅游文化学院信科系，云南 丽江 674199)

摘要：构建科学、准确的学龄儿童人数预测模型，对合理规划小学学校数量，制定小学教师招聘计划，制定人口政策具有一定的参考价值。根据预测误差平方和最小原则，利用Matlab循环语句命令编程，设定平滑系数α的一个精度，从0<α<1的所有值中选择最优α，研究发现利用该法建立的三次指数平滑模型在学龄儿童人数预测方面有较好的预测效果；在此基础上利用马尔科夫预测法，对三次指数平滑模型预测结果进行修正，弥补了因随机波动性导致的预测误差偏大的情形；通过对这两个模型预测结果的对比分析，表明三次指数平滑-马尔科夫模型的预测效果比单独利用三次指数平滑模型的效果有较大改善。

关键词：三次指数平滑；马尔科夫模型；学龄儿童

此处研究的“学龄儿童”是指“小学学龄儿童”，即符合普及小学义务教育入学年龄阶段的儿童。目前，学术界对学龄儿童的研究主要集中在安全、心理、教育、行为与失学等问题上。在中国知网上以“主题”或“篇名”为“学龄儿童人数预测”进行检索，未能检索到相关文献。对学龄儿童人数的预测有着较重要的意义，一方面，准确预测学龄儿童人数有利于合理规划小学学校数量，制定合理的小学教师招聘计划，从而既不造成社会资源的浪费，又能保证学龄儿童的入学。另一方面，如果学龄儿童人数少，则预示着将来可能存在高校招生难、人口老龄化等社会问题，准确预测学龄儿童人数可以对可能存在的社会问题提前做出应对，对制订人口政策提供参考。三次指数平滑模型在建筑事故预测与交通事故预测等方面有着广泛的应用，马尔科夫模型也被应用于煤自然发火与桥梁耐久性等问题的预测[1-4]。文献[5](2013)将一次指数平滑模型与马尔科夫模型结合，运用于巢湖水质的预测。此处尝试将三次指数平滑模型与马尔科夫模型进行结合，首先利用1992—2010年云南学龄儿童人数数据，分别建立三次指数平滑模型与三次指数平滑-马尔科夫模型；然后将两模型分别应用于2011—2013年云南学龄儿童人数的预测，与真实值进行比较，结果表明两个模型对该问题的预测都取得了较好的效果，且后者相较于前者在预测效果上有了明显的改进；最后，利用1992—2013年云南学龄儿童人数数据，再次建立基于三次指数平滑的马尔科夫模型，预测了2014—2016年云南学龄儿童人数。

1马尔科夫模型的建立

1.1三次指数平滑模型

三次指数平滑模型是一种用于短期内预测非线性趋势时间序列变化情况的模型。模型表达式如下：

(1)

(2)

(3)

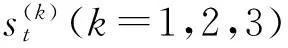
1.2马尔科夫预测

马尔科夫模型是通过对事物不同状态的初始概率与状态之间的转移概率的研究来预测事物未来状态的一种数学方法[6]。马尔科夫模型表达式为[7]

(4)

X(0)为初始状态概率向量，X(k)为经过k个时期后的状态概率向量，P为一步状态转移概率矩阵。该模型的建立包含状态划分、状态转移概率矩阵的确定和预测3个过程。

1) 状态划分。利用三次指数平滑模型的预测结果计算相对误差Δk,其中Δk的计算公式为Δk=(Yk-yk)/yk*100%。以相对误差的最大范围区间为基础，根据相对误差的具体情况得到K个可能状态⊗1,⊗2,…,⊗K，其中任一状态可表示为⊗i=[⊗i1,⊗i2]，状态划分具体情况见表2。

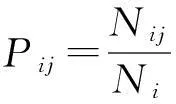
3) 预测。初始状态概率向量X(0)及一步状态转移概率矩阵P确定后，根据公式(4)可得到经过k个时期后的状态概率向量X(k)。

记三次指数平滑模型由初始时刻经过k个时期后的预测值为Y(k)，根据状态划分情况，得到Y(k)的K个预测区间，任一预测区间可表示为

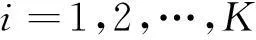
(5)

(6)

2实例分析

2.1数据收集

收集了1992—2013年云南省学龄儿童人数数据，数据来源于《云南统计年鉴》。首先用1992—2010年的数据建立三次指数平滑模型与三次指数平滑-马尔科夫模型，2011—2013年的数据用于测试模型；再用1992—2013年数据建立三次指数平滑-马尔科夫模型，预测2014—2016云南省学龄儿童人数。

2.2三次指数平滑模型的建立

利用1992—2010年云南省学龄儿童人数数据做散点图，发现数据基本呈曲线下降趋势。因为三次指数平滑模型一般适用于短期内曲线趋势时间序列的预测，故可选用该模型进行预测。先用1992—1994年云南省学龄儿童人数的平均值作为平滑指数的初值：

一般地，平滑系数α是根据经验从0.3，0.5与0.7等少数几个值中选取预测效果最好的一个。这种选取α的方法，虽然有一定的可取性，但是主观性较强。此处选取α的思想是根据预测误差平方和最小原则，利用Matlab循环语句命令编程，从0<α<1的所有值中选择最优α，这样选出的平滑系数更具客观性。在实际操作中，不可能取遍0<α<1的所有值，一般要先设定α的一个精度，取出最优α后看预测效果是否达到要求，如果没达到，再进一步提高精度。此处尝试设定α的精度为小数点后3位，即从999个α=0.001,0.002,…,0.999中选出最优值。按照前面选取α的思想，选择出最优α=0.720。

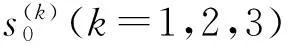
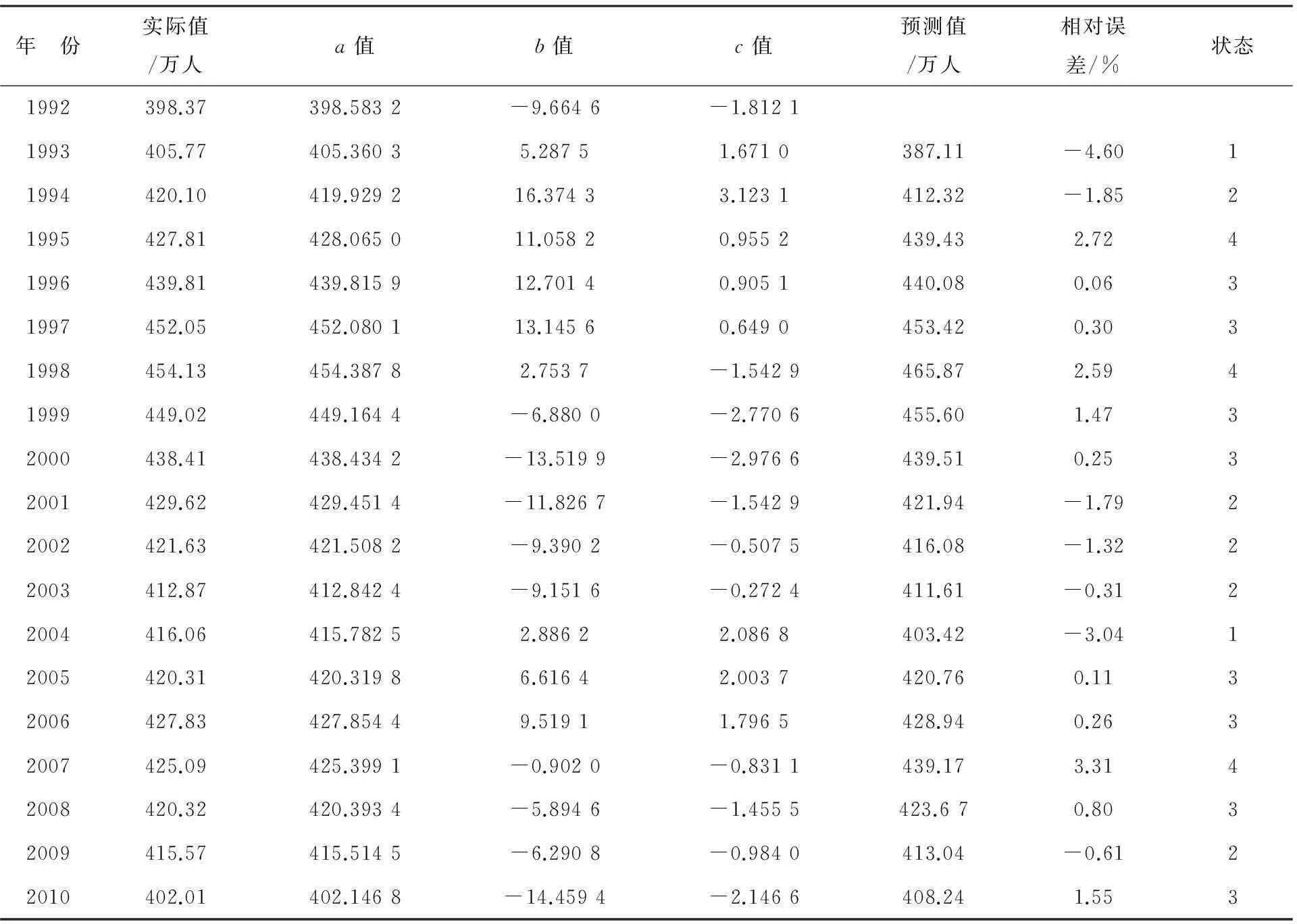
表1　三次指数预测结果与马尔科夫状态表

a2010=402.146 8,b2010=-14.459 4,c2010=-2.146 6

以2010年为起点，预测模型的表达式为

Y2010+T=402.146 8-14.459 4T-2.146 6T2

2.3三次指数平滑-马尔科夫模型的建立

三次指数平滑模型建立成功后，在其基础上可利用马尔科夫预测对其预测结果进行修正，进一步建立三次指数平滑-马尔科夫模型。首先进行状态划分，其原则是状态数一般取3～5个为佳，且必须保证区间内均有数据[7]。根据以上原则，结合模型一的相对误差最大范围区间 [-4.60%,3.31%]，以-5%,-2%,0,2%与5%为状态分界点进行状态划分，划分情况见表2。

表2　状态划分表

由表1 1993—2010年三次指数平滑模型每年相对误差所处的状态可得表3。表1表明，状态1转状态1不存在，状态1转状态2有1个(1993年转1994年)，状态1转状态3有1个(2004年转2005年)，……。总结以上状态转移情况，得到状态转移情况表(表3)。

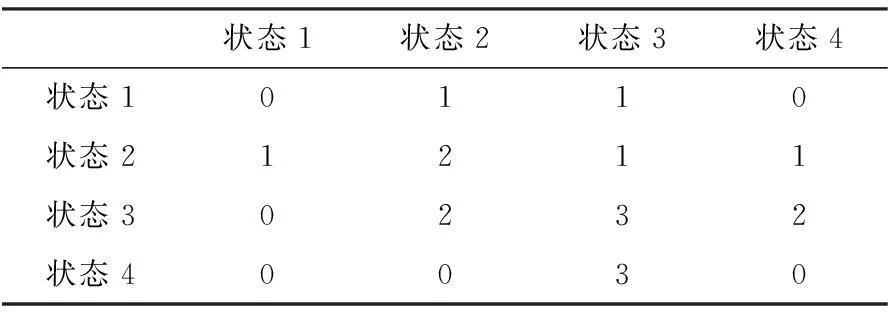
表3　状态转移情况表

由表3，计算出一步状态转移概率矩阵为

以2010年相对误差状态3为初始概率向量，即X(0)=(0,0,1,0)，在公式(4)中依次取k=1,2,3，计算出2011—2013年的状态概率向量。由三次指数平滑模型2011—2013年的预测值及表2的状态划分，用式(5)求出每年的预测区间；然后进一步可求出区间中值，得出每年的区间中值向量；最后，利用式(6)计算三次指数平滑-马尔科夫模型预测值，所有计算结果列于表4。

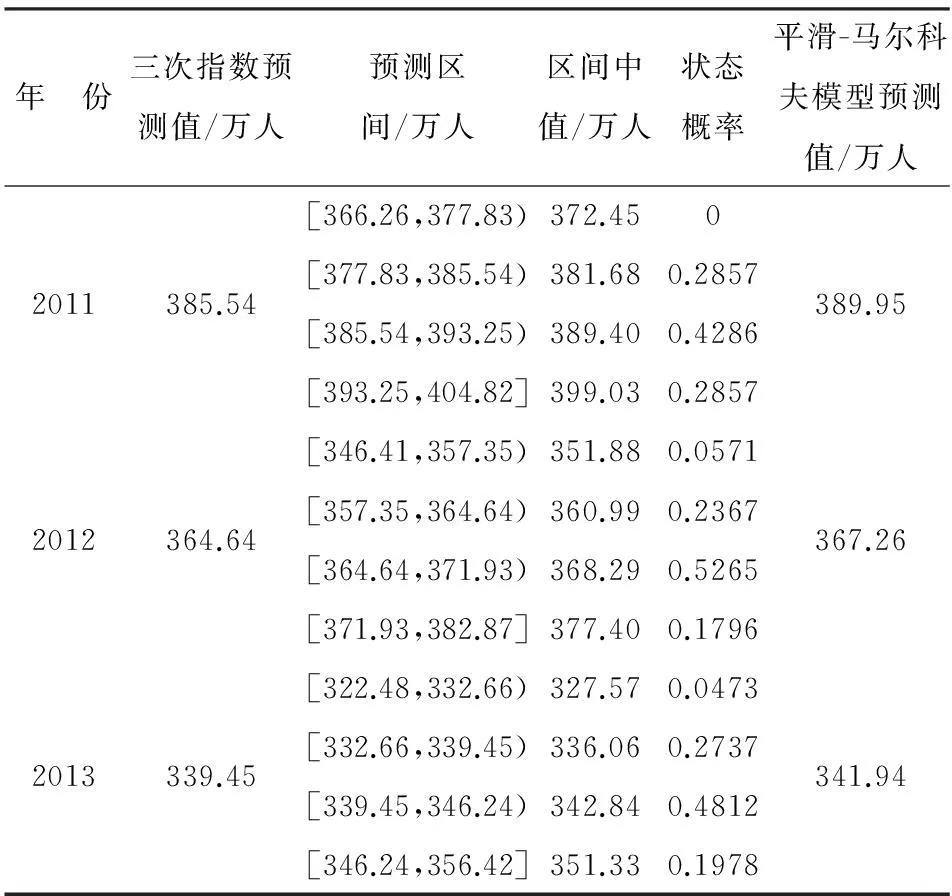
表4　三次指数平滑-马尔科夫模型预测结果表

为比较两种模型的预测效果，将两模型2011—2013年的预测值、相对误差与平均相对误差列于表5。

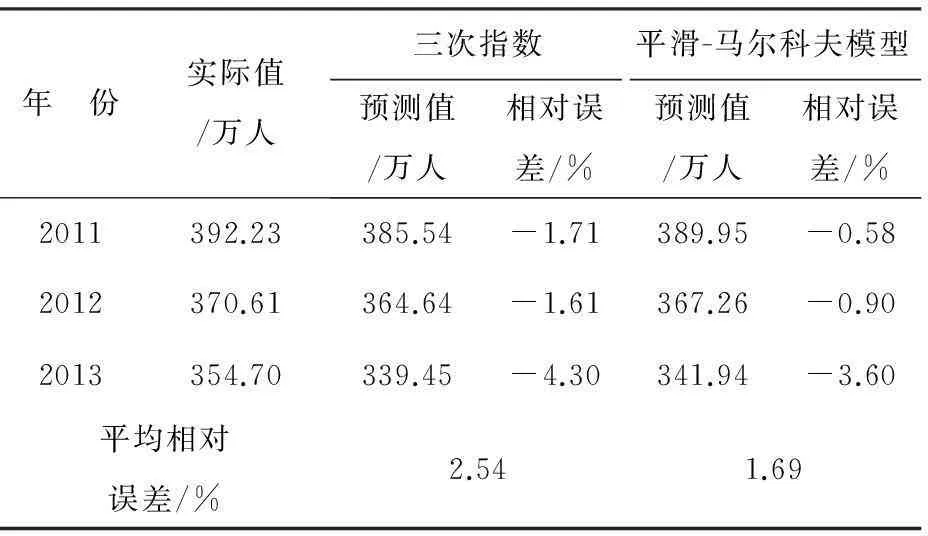
表5　模型测试情况对比表

由2011—2013年的两模型测试情况可见，在相对误差方面，平滑-马尔科夫模型每年的预测效果均优于三次指数平滑模型；在平均相对误差方面，平滑-马尔科夫模型为1.69%，相较于三次指数平滑模型的2.54%有了较大改善。由此可得，在云南学龄儿童人数预测这个问题上，平滑-马尔科夫模型的预测效果是优于三次指数平滑模型的。

为了更加合理利用原始数据的全部信息，使预测结果更加准确、可靠，利用1992—2013年全部数据与上文所述方法重新建立三次指数平滑-马尔科夫模型，对2014—2016年云南省学龄儿童人数进行预测，预测结果依次为333.20万人、311.62万人、288.42万人。

3结论

利用三次指数平滑模型对云南学龄儿童人数进行预测分析，取得了较好的预测效果，模型测试平均相对误差为2.54%。在此基础上，利用马尔科夫预测模型对三次指数平滑模型的预测结果进行修正，进一步提高了预测的精度，模型测试平均相对误差为1.69%。但是，因为三次指数平滑模型，通常只适用于短期预测，故文中建立三次指数平滑-马尔科夫模型也只在短期内预测较可靠。三次指数平滑-马尔科夫模型也可尝试用于其他省份学龄儿童人数的预测，或是尝试用于其他方面的预测研究。

由2014—2016云南学龄儿童人数预测数据可见，云南学龄儿童人数逐年递减，这预示着若云南省对现有状况不及时应对，则在不久的将来云南小学学校数量、小学教师人数相对于需求可能会偏多，造成社会资源的浪费；在更远的未来还可能导致高校招生难、人口老龄化等问题。

参考文献(References)：

[1]严小丽，何超，黄怡浪.三次指数平滑法在建筑事故预测中的应用[J].统计与决策，2015(10)：72-73

YAN X L,HE CH,HUANG Y L.Application of the Cubic Exponential Smoothing Method in Forecasting of Construction Accident[J].Statistics & Decision,2015(10):72-73

[2] 王洪德，曹英浩.道路交通事故的三次指数平滑预测法[J].辽宁工程技术大学学报(自然科学版)，2014，33(1)：42-46

WANG H D,CAO Y H. Cubic Exponential Smooth Method of Road Traffic Accident Forecasting[J].Journal of Liaoning Technical University(Natural Science),2014,33(1):42-46

[3] 王磊，武术静，李长青.灰色马尔科夫模型对煤自然发火预测的研究[J].河南理工大学学报(自然科学版)，2015，34(1)：35-39

WANG L,WU SH J,LI CH Q.Study on Prediction of Coal Spontaneous Combustion Based on Grey Markov Methed[J]. Journal of Henan Polytechnic University(Natural Science),2015,34(1):35-39

[4] 哈娜，付深远.基于改进灰色——马尔科夫的桥梁耐久性预测模型研究[J].中外公路，2015,35(3)：152-157

HA N,FU SH Y.Study on Prediction Model of Bridge Durability Based on Improved Grey Markov[J]. Journal of China & Foreign Highway,2015,35(3):152-157

[5] 荣洁，王腊春.指数平滑法:马尔科夫模型在巢湖水质预测中的应用[J].水资源与水工程学报，2013，24(4)：98-102

RONG J,WANG L CH.Application of the Exponential Smoothing Law-Markov Model in Prediction of Water Quality of Chaohu Lake[J]. Journal of Water Resources and Water Engineerin,2013,24(4):98-102

[6] 芮海田，吴群琪，袁华智，等.基于指数平滑法和马尔科夫模型的公路客运量预测方法[J].交通运输工程学报，2013，13(4)：87-93

RUI H T,WU Q Q,YUAN H ZH,et al. Prediction Method of Highway Passenger Transportation Volume Based on Exponential Smoothing Method and Markov Model[J].Journal of Traffic and Transportation Engineering,2013,13(4):87-93

[7] 熊祖强，王晓蕾.矿井相对瓦斯涌出量动态无偏灰色马尔科夫预测[J].安全与环境学报，2015，15(3)：15-18

XIONG Z Q,WANG X L. Application of the Markov Bias-Free Dynamic Grey Model for the Relative Gas Gush-Out Rate Predict[J〗. Journal of Safety and Environment,2015,15(3):15-18

责任编辑：李翠薇

Yunnan School-age Children Prediction Based onCubic Exponential Smoothing

PENG Nai-chi, DANG Ting

(Department of Information Science and Technology, Tourism and Culture College of Yunnan University, Yunnan Lijiang 674199, China)

Abstract：Construction of scientific and accurate forecasting model for predicting the number of Yunnan school-age children has certain reference value for the rational planning of the number of primary school, the development of primary school teachers recruitment plan, and the formulation of population policy. According to the principle of minimum sum of prediction error square, a precision of the smoothing coefficient is set up, the optimal smoothing coefficient is selected from all the values between 0 and 1, by using the Matlab loop statement programming. Research shows that the three exponential smoothing model established by this method has good prediction effect on the number of school-age children. On this basis, the forecasting results of the three exponential smoothing model are modified by using Markov forecasting method, which makes up for the forecast errors caused by random fluctuation. Through the comparison and analysis of the predicted results, it shows that the forecasting effect of cubic exponential smoothing-markov model is better than cubic exponential smoothing model. Finally, the number of 2014-2016 Yunnan school-age children is forecasted by using cubic exponential smoothing-markov Model.

Key words:cubic exponential smoothing model; Markov model; school-age children

中图分类号：O213

文献标志码：A

文章编号：1672-058X(2016)02-0049-05

作者简介：彭乃驰(1981-)，男，贵州黔东南人，讲师，硕士，从事应用统计学研究.

*基金项目：2015年度云南省教育厅科学研究基金一般项目资助(2015Y507).

收稿日期：2015-10-09；修回日期：2015-11-09.

doi:10.16055/j.issn.1672-058X.2016.0002.011