高考填空题复习要点指津

●王勇强　(湖州市教育科学研究中心　浙江湖州　313000)



高考填空题复习要点指津

●王勇强(湖州市教育科学研究中心浙江湖州313000)

1　题型解读

填空题是高考试卷中的三大题型之一．纵观浙江省这12年来的高考数学试题，填空题的题量由4题增加到7题，分值从16分增加到36分．由此可看出，高考填空题的复习越来越重要，高三复习教学时一定要重视，争取获得突破．

填空题和选择题一样，都属于客观性试题．它们都只要求写出结果而不需要写出解答过程，但是这2类题型却发挥了不同的考查功能．选择题相对重视概念的本质，要求判断准确．而填空题的主要特征是题目小巧，结构灵活，知识覆盖面广，重基础、概念与运算．除了考查基础知识、基本技能、基本数学思想方法和数学思维能力外，高考填空题的考查功能更关注考生运算的方法，要求考生的运算结果正确．

另外，从2015年起，浙江省数学高考形式也更加丰富，出现了一题多空的情形．多空题的出现，更好地分散了难点，让考生在填空题中也能分步得分，减少了考生由于失误而导致失分，体现了高考命题组的人文关怀．

2　方法指津

填空题复习首先要重基础、重概念，同时在求解过程中要重视课本、重视核心概念、重视基本思想方法的运用，重视各种解题方法的选择和必要的优化．同时，教师要引导学生加强解题后的反思，努力将问题的本质揭示出来，悟透本质则题变易．总之，复习时要努力提高学生分析问题、解决问题的能力．

对于填空题的复习教学，除了要努力提高学生分析问题、解决问题的能力外，更要重视和落实运算教学，提高学生的运算求解能力．教师在高三复习时要想方设法通过有效的复习教学，使学生对于填空题的分析、运算、求解水平从直接、准确，逐步提升到合理、迅速，直到灵活、巧妙．

另外，务必要牢记填空题不能小题大做，而要努力做到小题小做、小题巧做．

3　典题剖析

3．1重基础，基础不牢、地动山摇

分析本题考查双曲线的基本概念和基本量的运算，易知实轴长为2a=4，离心率为，焦点F(c，0)到渐近线bx±ay=0的距离d=类似于本题中求双曲线离心率的值或范围的问题是高考填空题的一个热点，主要解题策略是先通过定义、几何直观或代数运算找到双曲线3个基本量a，b，c中任意2个的等量关系或不等关系，再去求离心率的值或范围．

(2014年浙江省数学高考理科试题第16题)

分析根据条件易列出关于a，b的等量关系．将该双曲线的2条渐近线方程分别与x－3y+m=0联立，求得点A，B的坐标，从而得到AB的中点Q的坐标为

由|PA|=|PB|得，PQ与已知直线垂直，故

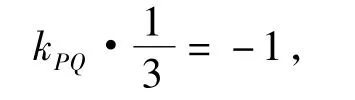
若将2条渐近线看成一个整体，则可适当减少运算量．联立方程

消去x或y，得到关于y或x的一元二次方程，再用韦达定理就可直接求出AB的中点Q的坐标，省略了求点A，B坐标的运算过程，后同前面解法．

变式2如图1，已知双曲线(其中a＞0，b＞0)，F1(－c，0)是左焦点，圆x2+y2=c2与双曲线左支的一个交点是P，若直线F1P与双曲线右支有交点，则双曲线的离心率的取值范围是______．

图1

分析先定性分析，再定量计算．根据条件易知，双曲线的离心率越大，开口越大，2条渐近线越靠近y轴．当直线F1P与渐近线平行，即时，直线F1P与双曲线右支没有交点;当时，直线F1P与双曲线右支有交点．若联立可计算出点P的坐标为，再通过，可计算出双曲线的离心率的取值范围是．这种解法思路清晰，但运算量较大，需要学生有较强的运算能力．而运用双曲线的定义与例1中得到的结论:双曲线的焦点到渐近线的距离为短半轴b，则能较快解决此题．当直线F1P与渐近线平行，即直线F2P与渐近线垂直时，可求出|F2P|=2b，|F1P|=2a，又由双曲线的定义得到|F2P|－|F1P|=2a，从而，故双曲线的离心率的取值范围是

3．2重方法，多法并举、多法选优

例2如图2，在三棱锥A-BCD中，AB=AC= BD=CD=3，AD=BC=2，点M，N分别是AD，BC的中点，则异面直线AN，CM 所成角的余弦值是______．

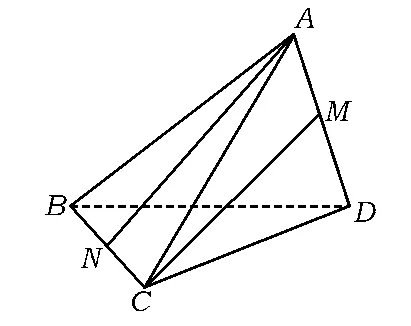
图2

(2015年浙江省数学高考理科试题第13题)

分析本题考查求异面直线所成角的问题以及空间想象能力和运算能力，故只需将空间问题平面化，通过平移将异面直线AN，CM所成的角转化到某个三角形的内角，运用余弦定理即可求出所成角的余弦值．当然，也可运用向量运算来解决这个问题．

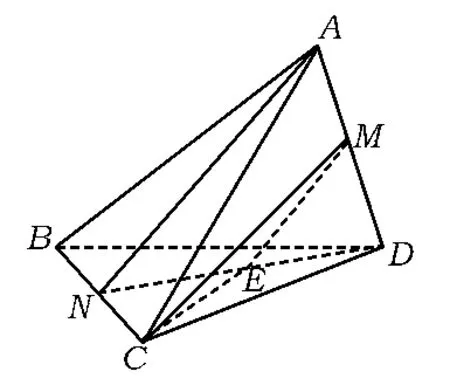
图3

解法1联结ND，取ND的中点E，联结ME，则ME∥AN，异面直线AN，CM所成的角就是∠EMC．由于的长度可在平面BCD中求出，从而运用余弦定理即可求出异面直线AN，CN所成的角的余弦值是

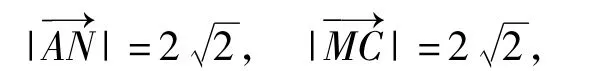
注不管是用解法1还是解法2，解题的关键是转化思想的运用，将空间问题平面化或向量化是解决立体几何问题的基本策略．而运用向量解决立体几何问题不仅仅是建立空间直角坐标系→标(设)出点的坐标→向量坐标化→向量运算→运算结果几何化这一种方法，还可以是像解法2这样不建系的向量方法．在平时教学时要多法并举，具体解题时可多法选优，选择适合自己的方法．

3．3重本质，本质凸显、运算趋简

例3在平面直角坐标系xOy中，设直线y= －x+2与圆x2+y2=r2(其中r＞0)交于点A，B，O为坐标原点，若圆上一点C满足，则r=______．

分析本题考查直线与圆的位置关系以及平面向量的基本概念与运算，可从坐标法这一解析几何的核心方法来分析求解，也可从平面向量的性质和运算并结合直线与圆的几何特性角度去考虑．如考虑用坐标法求解，则会将此填空题当成一个解答题去做，会造成“小题大做”的情形，影响解题的速度．

解法1设A(x1，y1)，B(x2，y2)，C(x，y)，由，得

过点O作AB的垂线交AB于点D，则

又因为圆心到直线的距离为

注解法1从平面向量坐标化入手，解法2从平面向量数量积的定义入手，解法3从平面向量共线定理入手，这3种解法的几何味越来越浓，揭示问题的几何本质属性也越来越深刻，从而使运算求解变得越来越简单．故解填空题不能小题大做，而要努力做到小题小做、小题巧做，必须合理灵活地运用恰当的方法，在“巧”字上下功夫．

3．4重规律，探求轨迹、解题直观

例4在△ABC中，内角A，B，C所对的边分别是a，b，c．若acosB=bcosA，且边BC上的中线AD的长为4，则△ABC 面积的最大值是______．

分析本题主要考查三角函数及其变换、正弦和余弦定理等基础知识，同时考查运算求解能力．由已知易得A=B，从而c=2acosA，及

另外，由已知可得|CA|=2|CD|，|AD|=4，若以A为原点、中线AD所在直线为x轴建立直角坐标系，则可求出顶点C的轨迹为半径是的阿波罗尼斯圆(挖掉2个点)，从而求得△ABC的面积的最大值是

此法从顶点C的轨迹入手，用解析法解决解三角形的面积最值问题，能发现三角形面积随顶点C的运动而发生变化的规律，从而揭示出问题的几何背景，让学生从根本上去理解该问题．悟透本质则题变易．

变式在锐角△ABC中，内角A，B，C所对的边分别为a，b，c．若，则△ABC 面积的最大值是______．

因为b2+c2≥2bc，等号当且仅当b=c时成立，所以

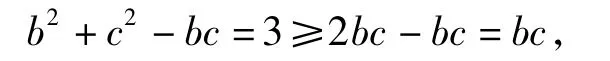
即bc≤3，故bc的最大值为3．因此△ABC的面积为

3．5重课本，核心概念、发挥作用

例5设函数f(x)=ax2－2ax+2－2b(其中a，b∈R)，当x∈［－2，2］时，f(x)≥0恒成立，则a+2b 的最大值是______．

分析本题主要考查不等式恒成立的问题，考查分类讨论和数形结合的思想方法．由题意可按a＞0，a=0，a＜0分类讨论，求出函数f(x)在x∈［－2，2］时的最小值f(x)min，由f(x)min≥0求出a+2b的最大值为2．当然也可避免分类讨论，将“当x∈［－2，2］时，f(x)≥0恒成立”等价于

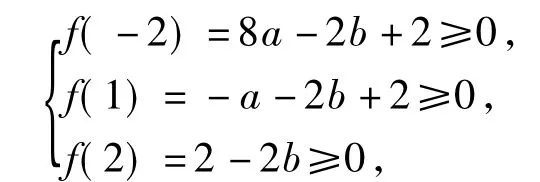
再用线性规划知识，求出a+2b的最大值为2．巧解由于1∈［－2，2］，故

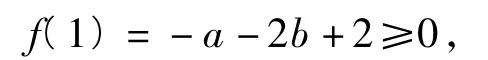
注这种灵活巧妙的解题思路并不突兀，而是源自课本，源自人教A版《数学(必修1)》第36页函数的最大值的概念．因此回归课本，重视核心概念的运用，在高三复习教学时显得尤为重要．

4　精题集萃

1．已知集合A={x|(x－2)(x+5)＜0}，B= {x|x2－2x－3≥0}，全集U=R，则A∩B =______，A∪(CUB)=______．

3．在数列{an}中，a2=2，a5=8．若{an}是等比数列，则公比q=______，若an是等差数列，则数列{an}的前n项和Sn=______．

4．已知实数a，b满足log2(a+b)=log4(4－4a2b2)．当b=1时，a=______;当a－b取到最大值时，ab =______．

5．已知⊙M:(x－1)2+(y－1)2=4，直线l: x+y－6=0，A为直线l上一点，若⊙M上存在2个点B，C，使得∠BAC=60°，则点A的横坐标的取值范围是______．

8．已知函数f(x)=x2+mx－1，若对于任意的x∈［m，m+1］都有f(x)＜0，则实数m的取值范围为______．

9．已知a，b是不共线的2个向量，且a·b＞0，|b|≥4．若对任意m，n∈R，|a+mb|的最小值是1，|b+na|的最小值是2，则a·b的最小值是______．

参考答案

1．{x|－5＜x≤－1}，{x|－5＜x＜3}