玩转数形结合 提升数学思维——数学思想与解题方法专题之数形结合思想

●伊建军　(杭州高级中学　浙江杭州　310003)



玩转数形结合提升数学思维
——数学思想与解题方法专题之数形结合思想

●伊建军(杭州高级中学浙江杭州310003)

1　知识内容

我国著名数学家华罗庚曾说过:“数缺形时少直观，形少数时难入微;数形结合百般好，隔离分家万事休．”数形结合是高中数学中一种非常重要的数学思想，几乎可以渗透到高中数学的所有知识点中．比如向量、解析几何就是“数”与“形”结合的完美产物，因此可以说，数形结合涉及到的范畴非常之广．笔者在此要强调的是，我们在教学过程中要引导学生对问题深入思考，巧用、妙用“数形结合”思想，让学生体会“数形结合”思想在解题过程中的优越性，感受其强大的功能．

2　命题分析

近几年的高考数学命题有一种“小题考方法，大题考运算”的趋势，选择题、填空题的解决需要在熟练掌握数学知识的基础上运用各种数学思想方法，其中数形结合是最为常见的数学思想方法之一．同样在解答题中，也经常利用数形结合思想帮助理解、分析题意，对快速解决问题很有帮助．

数形结合不仅在解题中广泛使用，而且在命题过程中也经常运用．在教学过程中，教师可以带领学生探索数学问题的命制过程、意图，解开数学命题的神秘感，寻找不同数学问题之间的横纵联系，挖掘出蕴含其中的数形结合思想．

3　典题剖析

3．1变换结构，注意动静结合

解题时，研究题目中所给式子的结构特征，并适当地进行一些变换，有意识地利用数形结合的思想方法，可以进行一些转化，比如转化成比较熟悉的函数、不等式或几何中的常见曲线方程等．另外，在转化过程中，一般不要让多个图形同时含有参数，同时变化的图像会增加难度．因此，想办法分离参数，让图像一动一静，动静结合，可以化难为易，迎刃而解．

例1已知实数a，b都不为0，求证:函数f(x)=3ax2+2bx－(a+b)在(0，1)内一定有零点．

分析本题如果直接用二次函数来解决，需要进行分类讨论，由于含有2个参数a，b，因此讨论起来较为复杂．若我们把参数适当分离，将f(x)=0化为a(3x2－1)=－b(2x－1)，再进一步转化为3x2－1=，则等式的一边含参数，另一边不含参数，实现了函数图像的一动一静，可以通过数形结合来解决．如图1，函数y=与函数y=3x2－1在(0，1)之间必有交点．

图1

通过该问题的解决，可以进一步理解数学命题的意图，同时图形的直观性也让人感觉到数学问题的巧妙．

A．当a＜0时，x1+x2＜0，y1+y2＞0

B．当a＜0时，x1+x2＞0，y1+y2＜0

C．当a＞0时，x1+x2＜0，y1+y2＜0

D．当a＞0时，x1+x2＞0，y1+y2＞0

分析虽然f(x)与g(x)都是比较熟悉的函数，并且也是一动一静，可以直接画图再结合运算来完成．若适当变形，则能更方便地解决问题:由得，然后对与y= ax+b的图像进行分析．一个小小的变换，带来的是大大的方便!

图2

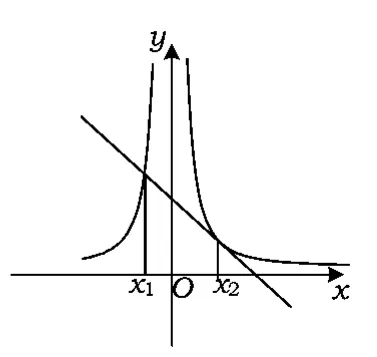
图3

故选B．

2　理解本质，抓住几何特征

每一个数学问题，都有一些本质的特征，从哪个角度去理解，是确定哪一种解题思路的关键．事实上，有许多代数问题中隐藏着它的几何特征，抓住了这个特征，运用数形结合的思想，不仅可以顺利地解决问题，而且可以更清晰地理解问题．

例3若a，b，c满足:|a|=|b|=2，|c|=1，且(a－b)·(b－c)=0，则|a－b|的取值范围是______

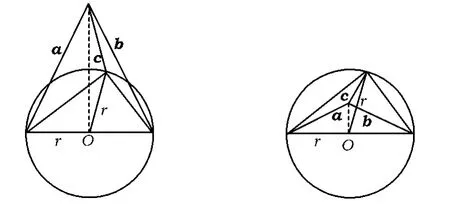
图4

分析向量问题的解题思路可谓是千变万化，但许多向量问题其实都与几何知识有关，因此，数形结合思想在向量中有着广泛的应用．我们平时在编写一个向量问题时其实也常常从几何方面入手，数形结合思想在向量中通常是首先需要考虑的方法．本题抓住2个特征:一个是模长为定值;另一个是(a－c)·(b－c)=0，显然具有垂直的特征．可构造这个问题的几何图形(分如图4所示的这2种情况)，|a－b|=2r(其中r＞0)，于是

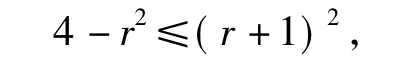
3　运用类比，注意横向联系

波利亚在《怎样解题》一开始拟定计划中说道:“你以前见过它吗?你是否见过相同的问题而形式稍有不同?”我们在拿到一个数学问题时，你去思考过这个问题吗?事实上，在一个数学知识点中出现的式子，有时候却具有另一个知识点的特征;在一个问题用过的方法，可以考虑能不能在另一个问题中使用，实现多题一解，事半功倍，从而提高综合解决问题能力．

例4若等差数列{an}满足，则的最大值为______．

分析这明显是一个数列问题，但如果仅用数列知识来解决，发现难度较大，特别是已知条件中的，平方以后较为复杂．如果把a1和

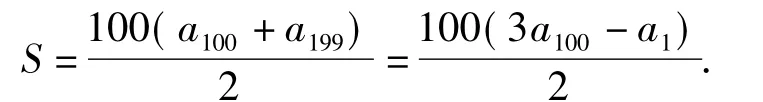
那么问题是不是可以转化为:已知x2+y2≤10，求目标函数z=50(3y－x)的最大值了呢?结合线性规划的方法，利用数形结合可得到最大值为500，问题变得较为容易．

4　数形相助，避免错看误算

数形结合，应该是数与形2种方法的有机结合，千万不要理解成只要画出图形就可以了，况且，要画出完全正确的图形困难很大，有时甚至是不可能做到的．并且，很多时候，图形也只是对解决问题起到一种辅助作用．因此，数形结合，不能只注重其中一个方面，而应该相互依赖，相辅相成，互相兼顾，达到完美结合．

分析对数函数与二次函数是我们比较熟悉的函数，但在画出2个函数的图像后，要进行相应的计算，这样才能得到正确的结果，同时要注意函数图像的变化趋势．

由f(x)=0得

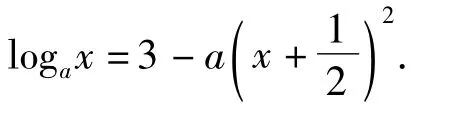
当a＞1时，画出g(x)=logax和h(x)=3－的图像(如图5所示):只要满足h(1)≥ 0即可，解得

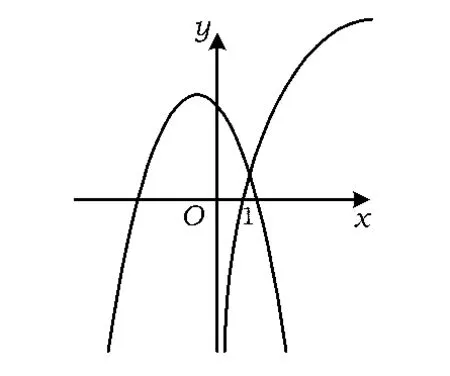
图5

图6

当a＜1时，画出g(x)=logax和h(x)=3－的图像(如图6所示)，此时h(1)=3－，故在(0，1)之间必有零点．

4　精题集萃

图7

A．x1x2＜0B．x1x2=1

C．x1x2＞1D．0＜x1x2＜1

5．已知点P到2个定点M(－1，0)，N(1，0)距离的比为，点N到直线PM的距离为1，则直线

PN 的方程为______．

6．如图8，已知直线l⊥平面α，O为垂足，长方体ABCD-A1B1C1D1中，AD=5，AB= 6，AA1=8，A∈l，B1∈α，则OC1的最大值为______．

图8

7．设t∈R，若n∈N*时，不等式恒成立，则t 的取值范围为______．

8．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知，求sinB和 cosC．

1)当a=0，b=1时，写出函数f(x)的单调区间;

3)若对任意实数a，b，总存在实数x0∈［0，4］使得不等式f(x0)≥m成立，求实数m的取值范围．

(2015年浙江省学业水平考试第34题)

参考答案

8．解注意到

如图9，构造△ABC，使AD= BD，则

图9

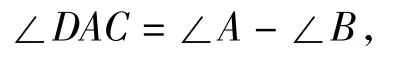
于是(5－x)2=x2+42－2·x·4cos(A－B)，解得x=4，从而

9．解1)f(x)的递增区间为(1，+∞)，递减区间为［0，1］．

3)命题“若对于任意实数a，b，总存在实数x0∈［0，4］，使得不等式f(x0)≥m成立”的否定形式为“若存在实数a，b，对任意的x∈［0，4］，不等式f(x0)＜m恒成立”．

图10