电流变夹层板滑模振动控制

陈春强，陈前(南京航空航天大学机械结构力学及控制国家重点实验室，南京210016)



电流变夹层板滑模振动控制

陈春强，陈前
(南京航空航天大学机械结构力学及控制国家重点实验室，南京210016)

摘要：为实现板结构振动控制，基于滑动模态控制思想，设计适用于电流变夹层结构的变刚度控制器，并且推导两类控制律——滑模控制律和简化的开关控制律。先将电流变液处理为可控黏弹性材料，基于Hamilton原理建立电流变夹层板有限元模型。设计滑模控制器时，首先将系统变换到模态空间，然后利用LQR最优控制理论设计控制面函数，设计电流变夹层板的滑模控制器，最后给出两个近似的半主动控制律。对悬臂电流变夹层板进行仿真分析，设计的滑模控制器能显著降低电流变夹层板振动水平，均方根降幅达到88.23%，取得明显优于被动控制的减振效果，体现电流变夹层结构在板结构振动控制应用中的前景。

关键词：振动与波；电流变液夹层板；有限元法；滑模控制；半主动控制

航天领域的太阳帆板、大型桁条、空间壁板等结构，因为柔性大、结构阻尼小的原因，扰动可能引发长时间、大幅度的振动，从而影响器件的工作性能，甚至结构安全，除了采用被动的阻尼技术，半主动的振动控制手段也是值得关注的。电流变夹层结构(Electrorheological sandwich structure，ER夹层)是一种用于振动控制的新型智能结构，可直接布置在梁、板等结构上，配合合适的控制算法还能实现智能振动控制，能在较小的能量代价下具有优越的减振、降噪性能。因其在振动控制领域有广阔的应用前景，引起了研究者的广泛关注。

国内的学者孟光[1]、任建亭[2]等人较早地对ER夹层梁、板结构进行相关的建模、实验研究，分析电场强度、厚度比等对结构特性的影响，得到丰富的研究成果。近年来，Jia和Chen等人利用有限元法建立电流变夹层板的模型，分析电场强度和厚度比对电流变夹层系统动力学特性的影响，在此基础上分析矩形电流变夹层板的动力学稳定性[3]，并对环形夹层板建模分析[4，5]；Kumar[6]分析用电流变夹层板组成的盒状结构，比较了多种表层材料情况下，外加电场强度对结构的模态频率和损耗因子的影响。最近，Jafar和Jalil[7]讨论边界约束条件对ER夹层结构瞬态响应的影响，发现电场增强则瞬态响应线性衰减，可见众多研究还是集中在试图通过施加外场、提高结构阻尼从而达到减振的目的。然而作为一种可控的智能结构，不仅需要研究其动力性特性，更应该关注振动控制算法的设计，比如学者杨智春、张培强等采用的模糊控制算法，笔者也对ER夹层梁的模糊控制进行过分析[8]。此外，在电流变液夹层结构研究的早期，受到结构模态频率可移动的启发，研究者最先设想的是电流变夹层结构的频率控制策略，其主要思想是把输入主频率和预先获得多电场条件下的频响函数比对，选取频响最小的电场输出。频率控制中需要快速获得较准确的实时频率，但目前瞬时频率的识别方法还不成熟[9]，可能正是这个原因限制了该类型控制策略的发展。滑模控制(Sliding Mode Control，简称SMC)也称变结构控制，它适合在控制过程中系统参数不断变化的变刚度和变阻尼控制，电流变夹层板正是这样的系统。滑模控制方法在半主动控制装置——车辆ER悬挂、抗震AVS阻尼器[10]等控制系统中，取得了很好效果，但文献对于在电流变夹层结构上应用滑模控制策略的研究还较为少见[2]。

以板结构振动控制为目标，首先建立电流变液夹层板有限元模型，并将动力学方程变换到模态坐标组成的状态空间；然后在状态空间中设计主动控制系统的滑模控制器，并且进行相关的近似，获得两类电流变夹层系统适用的半主动滑模控制律。最后，还对单边固支的电流变夹层板系统进行数值仿真，多种激励下的对比控制结果表明给出的半主动滑模控制律是有效的。

1　电流变夹层板的有限元模型

电流变夹层板是由上下两层弹性材料和中间电流变材料层组成，四周用硅橡胶密封，如图1所示。为简化分析，做以下简化假设：

(1)夹层板各层的横向变形相等；

(2)夹层板的上下表层的剪切变形忽略不计，不考虑上下表层的阻尼；

(3)相对于表层材料，电流变液的拉伸刚度、弯曲刚度很小，忽略不计；

图1　电流变夹层板控制系统示意图

(4)各层分界面上无相对滑动，夹层板处于小变形状态。

图2所示是夹层板在xz截面内的位移，下标u、e、d分别表示上表层、电流变层和下表层。按照变形协调有位移关系，可得电流变层的x向位移为

图2　电流变夹层板在xz面内的运动示意图

αy、βy分别是电流变层绕y轴的旋转角和剪切角，按照假设条件和图示的变形协调，可得

1.1单元自由度及形函数

采用具有四个节点的矩形单元，长宽分别为2a、2b，每个节点有七个自由度，记为δi={δi,jδi,kδi,pδi,q}，式中j，k，p，q是该单元的节点编号，其中j节点的位移为。

单元任意点的位移用四个节点的位移插值表示，即

式中N是对应于节点各位移的形函数矩阵，将其代入变形关系式(1)，可得电流变层位移形函数。

这里，四节点的位移分量相应的是四个已知边界条件，并考虑单元的对称性，参考平面矩形双线性单元和矩形薄壳单元[11]，选取位移形函数，此处略去不表。

1.2单元运动方程

用形函数表示单元势能、动能和外力的功，并代入Hamilton变分公式，可以获得i单元的振动方程为

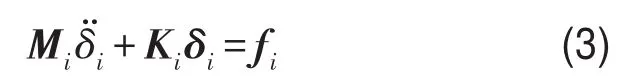
式中Mi和Ki是i单元的质量、刚度矩阵。

2　动力学方程和状态方程

如图1，电流变夹层板单边固支，按照该边界条件对单元坐标进行集成，并且考虑外加电场的作用，可以获得电流变夹层板系统的控制方程为

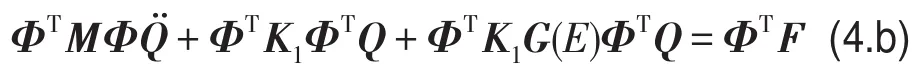
式中fi是ΦTF向量的i元素，qi(t)是近似的实模态坐标。

设计滑模控制律需要系统的简约形式的状态方程，所以将模态方程组(5)整理可得

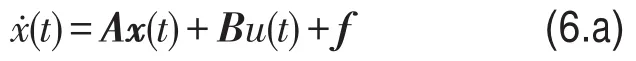
把上式划分为

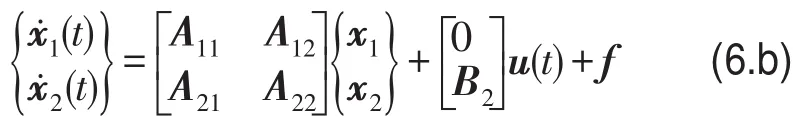
3　滑动模态控制器设计

3.1基于LQR最优控制理论的控制面函数设计

滑动模态控制的关键是设计控制面函数，设控制面函数S为状态变量x¯的线性组合，即

相应的，类似式(6.b)，对控制面S分块改写为式中，系数矩阵C1和C2是待求的，上式中把x2视作x1的控制，忽略状态方程中模态激励f，可得

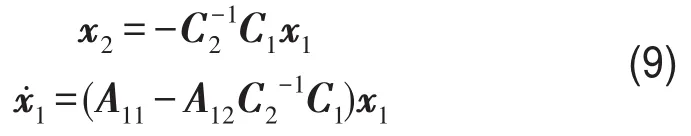
定义控制系统的性能指标

所以性能指标式(10)化为

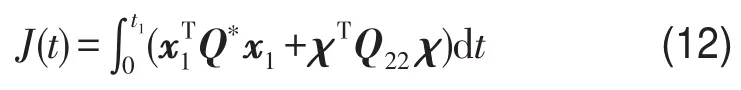
根据最优控制理论，容易求出控制面系数矩阵C

其中p¯是由式(16)确定的Riccati方程的解，控制面系数矩阵由权矩阵完全确定，实际应用时需要在控制前离线计算获得。

3.2确定滑模控制律

应用Lyapunov直接法确定电流变夹层系统的开关控制律。设Lyapunov函数为

系统在滑动面上渐进稳定的充分条件是

代入式(14)和式(15)，可以导出

其中λi是行向量的元素，Gi是列向量的元素。主动控制系统中实现该式的滑模控制，是用式中控制力保证为负定，但电流变夹层板是一种半主动的控制装置，保证时刻为负定较为困难，特别是控制力方向达不到要求时，参考文献[9]的做法，调整控制力使得尽量小，所以问题转变为解出使得最小的电场强度E。

控制中需要附加刚度系数与电场强度关系的向量，在离线状态下，先将电场强度离散为r个值E={E1E2…Er}，代入式(6.b)、式(16)计算得到，分别求取关于电场强度的关系，即

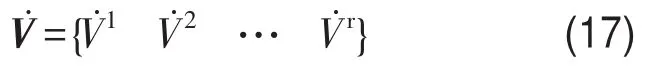
特别的，当系统的外激励频率在i阶模态频率附近，即系统振动存在主模态时，系统i阶模态的响应qi为主要响应，即λiui决定了整体值的符号，实际上此时的滑模控制律退化为开关控制律

控制律表达式(23)是不连续的，在振动控制中可能引起抖振，因此需要用连续的控制电场来代替不连续的控制电场，设计饱和控制律为

式中ε是滑动层宽度。至此，得到在电流变夹层结构可用的滑模控制的两种控制律表达式。如果对模型进行模态截断前m阶模态，控制器只需m个模态位移和模态速度作为输入。

4　仿真与计算

为验证有限元建模方法的正确性，采用与文献[4]、[5]相同参数的夹层板，计算固有频率和模态损耗因子，如表1所示，从两者对比结果看，两者吻合很好，说明了建模方法是可靠的。

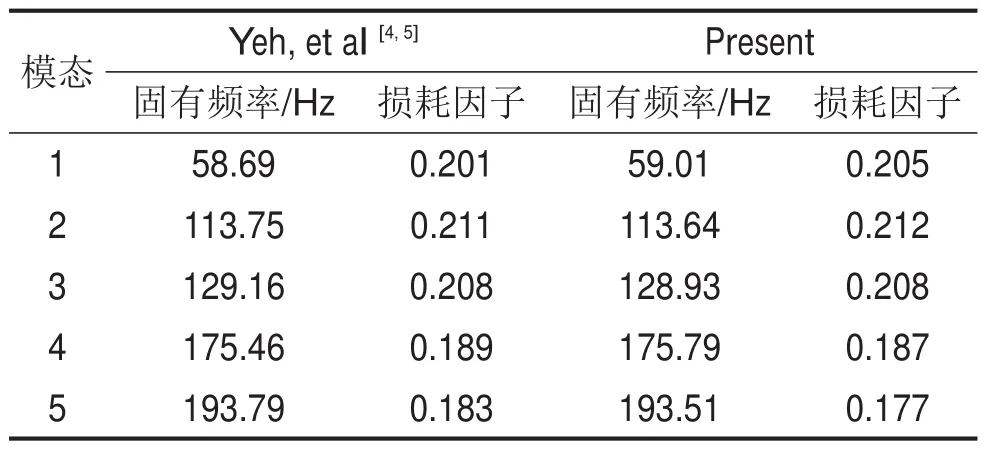
表1　固有频率和模态损耗因子对比

如图1，电流变夹层板左边固支，基本参数：长为360 mm、宽为240 mm，上下两层铝板厚度为1.0 mm，密度为2.7×103kg/m3，弹性模量为71 GPa，泊松比为0.3。对于小幅振动的电流变夹层结构，设其剪切模量为G=G′+G″，参考文献[5]引用Don的研究成果，取弹性模量G′=15 000 E2Pa，损耗模量G″=6 900 Pa，单元是30 mm×30 mm的矩形夹层板单元。

为检验提出的滑模控制在电流变夹层板振动控制系统中的有效性，对系统进行仿真分析，控制器相关参数为：控制面权重Q11=100 In×n，Q22=In×n，控制阶次m =4，滑动层宽度ε=0.02。如图1所示，在据边界1/3处的P点有z向简谐激励pz(t)=p0sin(ωt)，p0取单位值，频率从1 Hz～65 Hz，把稳定后的均方根值作为频率响应，分析系统的控制效果。图3为分别采用被动控制(恒定电场强度1.5 kV/mm)和滑模控制(电场强度上限Eb=1.5 kV/ mm)时，P点横向位移的频响函数变化曲线。

图3　被动控制和滑模控制作用下P点横向位移(Eb=1.5kV/mm)

从图中可以看出，当施加强度为1.5 kV/mm的恒定电场时，频响曲线向高频移动，并且具有更高的共振峰值，表明模态阻尼比在恒定电场下减小了。这表明，对于阻尼性能不随外加电场提高的电流变材料，简单施加恒定电场的被动控制是无效的，也就是说对于文中采用的计算模型，最优的被动控制实际上是无控工况（电场强度为零）。滑模控制下，P点位移响应的共振峰得到很好的抑制，这表明滑模控制器比被动控制具有更好的振动控制效果。同时也注意到，在原系统反共振频率附近，滑模控制没有控制效果，这是由于电流变夹层板结构的性能所限，滑模控制器也是有频段限制的。考虑激励是包含前四阶模态频率的随机激励，其频带为1 Hz～65 Hz，图4给出了测点P在无控和SMC控制下随机激励工况的位移时域响应，从图中可以看出SMC控制在时域范围内很好地抑制了位移振动响应，观察点P的均方根减小了88.23%。

为验证式(19)给出的模态附近开关控制律，考虑激励是在第1阶模态频率附近(3.5 Hz～7.5 Hz)的快扫频激励，分别采用两种控制律进行控制，控制电场强度上限Eb取较小的1 kV/mm。图5是P点响应变化的时间曲线，从图5中可以看出，两种控制律对系统的位移响应有较好的控制效果，采用开关控制律时，该点位移的均方响应相比无控制时减小了68.14 %，而采用饱和控制律时，均方响应减小了52%。比较而言，开关控制律取得控制效果略好些，但是采用饱和控制律的控制器输出的控制力是连续值，对系统的冲击小，所以对控制结构的加速度也是有利的。需要指出的是，这里给出的开关控制律需要获知当前结构振动的主要模态，因此只对确定性系统的振动控制较为合适。

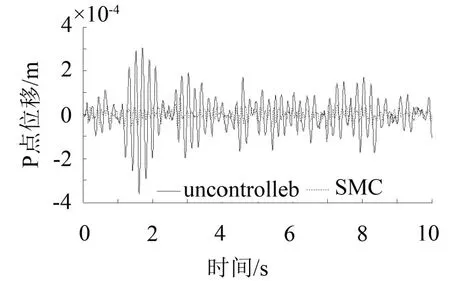
图4　无控制和滑模控制作用下P点横向位移(Eb=3kV/mm)

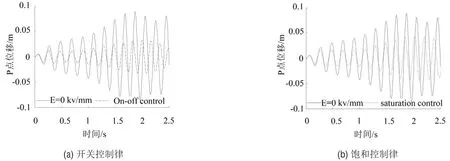
图5　两种控制下P点横向位移变化的时间曲线(Eb=1kV/mm)

5　结语

基于LQR最优控制理论设计适用于电流变夹层的滑模变结构控制器，实现对板的半主动振动控制，通过分析获得了以下结论：

(1)对电流变夹层板施加电场，结构的固有频率和模态损耗因子发生变化，模态频率向高频移动，表明刚度随着电场强度的增大而增大，并且在零电场条件下，结构具有一定的阻尼性能，这表明当智能控制失效时，电流变夹层仍然能降低板的振动水平。

(2)对于简谐激励和随机激励工况，电流变夹层结构采用滑模控制系统，总能取得优异的减振控制效果，随机激励工况下，采用较高的控制电场，均方根降幅接近90 %；当系统的激励频率在某阶模态频率附近，即振动存在主要模态时，采用开关控制相对于饱和控制律能取得更好的控制效果，而饱和控制律可以减小控制力对系统的冲击。

(3)设计的滑模控制器对其他边界条件的电流变夹层板、梁系统也是适用的。

参考文献：

[1]孟光，鲁宏权，任兴民.电流变液夹层板结构动态特性及振动控制的实验研究[J].航空学报，1998，19(4)：456-461.

[2]任建亭，吴克恭，闰云聚，等.电流变液夹层梁滑模振动控制的研究[J].机械强度，2002，24(2)：180-184.

[3] Jia-yi Yeh, Lien-wen Chen. Dynamic stability analysisof a rectangular orthotropic sandwich plate with an electrorheological fluid core[J]. Composite Structures, 2006, 72:33-41.

[4] Jia-yi Yeh. Vibration control of a sandwich annular plate with an electrorheological fluid core layer[J]. Smart Mater. Struct, 2007, 16:837-842.

[5] Jia-yi Yeh, Jiun-yeu Chen, Chin-tien Linc. Damping and vibration analysis of polar orthotropic annular plates with ER treatment[J]. Journal of Sound and Vibration, 2009, 325:1-13.

[6] Kumar K Ram, Ganesan N. Vibration and damping studies on a hollow sandwich box column with a viscoelastic/ electrorheological/magnetorheological fluid core layer by the finite element method[J]. International Journal of Structural Stability and Dynamics, 2008, 8(4):531-546.

[7] Jafar Rahiminasaba, Jalil Rezaeepazhand. Effect of boundary conditions on transient response of sandwich plates with electrorheological fluid core[J]. Key Engineering Materials, 2011, 462-463:372-377.

[8]陈春强，陈前.电流变夹层的半主动振动控制[J].噪声与振动控制，2013，33(3)：12-15.

[9]许鑫，史治宇，龙双丽.基于小波状态空间法的时变结构瞬时频率识别[J].中国机械工程，2011，22(8)：901-904.

[10]谭平，周福霖.新型主动变刚度阻尼器的滑动模态控制及仿真分析[J].华南地震，2007，27(2)：1-10.

[11]张昭，蔡志勤.有限元方法与应用[M].大连：大连理工大学出版社，2012.

Vibration Control of an Electrorheological Sandwich Plate Using Sliding Control Method

CHEN Chun-qiang , CHEN Qian
( StateKey Laboratory of Mechanicsand Control of Mechanical Structures, Nanjing University of AeronauticsandAstronautics, Nanjing 210016, China)

Abstract:Based on the sliding mode control algorithm, a new active variable stiffness controller was presented and employed to deduceboth control laws:continuoussliding modecontrol law and ON-OFF sliding modecontrol law. First of all, assuming that the electrorheological (ER) fluids behave as viscoelastic materials and their storage modulus and loss modulus depend on the applied electric fields, the kinetic equations of a sandwich plate with the ER materials layer were derived based on the Hamilton’sprincipleand finiteelement method (FEM). Theeffectsof theelectric fieldson thenatural frequenciesand modal lossfactorsof thesandwich platewereobtained. Thekinetic equationsof thesandwich platesystem weretransformed to amodal system beforedesigning thesliding modecontroller. Then, thesliding surfacewasdesigned by LQR optimal control theory, and two semi-active control laws were proposed. The results of numerical simulation of a cantilever ER sandwich plateshow that thiscontrol method isvery effectivein attenuating thestructural vibration. Themean square root of displacement at point Phas depressed about 88%. The attenuation effect is much better than that of passive control.

Key words:vibration and wave; electrorheological(ER) sandwich plate; finite element method; sliding mode control; semiactivecontrol

通讯作者：陈前(1951- )，男，教授，博士生导师。主要研究方向为振动控制、故障诊断。E-mail:q.chen@nuaa.edu.cn

作者简介：陈春强(1987- )，男，博士研究生。主要研究方向为振动控制、减振降噪。E-mail:cchen.detec@nuaa.edu.cn

基金项目：中央高校基本科研业务费专项资金资助项目；江苏高校优势学科建设工程资助项目

收稿日期：2015-07-14

文章编号：1006-1355(2016)02-0194-05

中图分类号：O241；O328

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.043