结合部等效参数在往复式压缩机管线振动分析中的应用

王　莹，赵　杰，刘　录，李　峰，袁　伟（北京石油化工学院机械工程学院，北京102617）



结合部等效参数在往复式压缩机管线振动分析中的应用

王莹，赵杰，刘录，李峰，袁伟
（北京石油化工学院机械工程学院，北京102617）

摘要：为了解决大型往复式压缩机机组及管线振动问题，建立有效的数值计算模型，将基于等效参数的动力修改技术与基于有限元的管线振动特性分析方法相结合，提出利用结合部等效参数修正有限元模型的方法，通过将管道与附件结合部作为弹性约束处理，并进行等效刚度优化，从而还原工程现场真实振动模型。以真实模型为基础进行模态分析，结合现场实测数据，找出管线振动原因，再次利用等效参数识别技术提出改造方案，改造后管线避开了原共振频率，减振幅度达到95.4%。该方法对于所建工程现场数值模型的有效性具有重要指导意义。

关键词：振动与波；有限元；等效刚度；动力修改；结合部；弹性约束

往复式压缩机管线系统受周期性的激振力作用，产生剧烈振动，轻则引发噪声污染，重则破坏与管道相连接的附属设备，甚至会造成巨大生命财产损失。针对管线剧烈振动的问题，需要准确有效且快速的方法对机械结构系统进行分析和改造，往复式压缩机及其管线系统是由许多管道和附件按流体走向结合起来的整体，系统中机体、缓冲罐、换热器、分离器、支架与管道之间相互接触的部分为机械结合部。研究表明，机械结构结合部在接触区域的刚度在机械结构总刚度中约占60 %～80 %。因此，当研究机械结构系统的动力特性时，应当考虑结合部刚度对系统动力特性的影响[1]。传统的做法主要借助有限元软件计算，把管道与附件接触处视为刚性连接[2–4]，这样处理简化了有限元计算模型，但是在实际工作中与管道相连接的附件时刻处于振动状态，并不像以往模型中定义的完全固定，因此需要对模型的边界条件进行处理。有学者[5]采用了基于有限元模型的管线系统动力修改方案，将非结合部约束位置作为参变量进行动力特性的结构优化设计，但未对结合部即边界条件做等效参数处理。由此，将机械结构动力修改理论与管线振动特性分析方法结合起来，引入结合部等效参数概念，用结合部等效刚度表达结合部边界条件，建立能够有效模拟机械结构动力特性的有限元模型，以还原真实的振动现场，进而分析振动原因，最终决定如何进行结构动力特性修改以消减管线振动。详细分析过程如图1所示。

图1　动力修改流程图

1　结合部等效参数动力学建模原理

管线与附件结合部在激振力作用下的动力学行为本质上是因为它们是弹性+阻尼的柔性结合。研究指出，机械结构中结合部的柔度和阻尼占总柔度、总阻尼的比重很大[6]。对模型进行简化计算时，可将相互焊接在一起的结合部分离为两个刚性结构通过弹性元件+阻尼元件的交界面连接。当附件结构产生振动位移时，会使管线结构位置发生微小变化，交界面也因此如弹簧受迫压缩和拉伸，该部位将产生复杂的动力特性，可以用柔性联接来等效。实际结合部联接方式可用三个方向三个交界面上的三对弹性元件和阻尼元件来等效。现以结合点一个方向的联接为例来说明其约束条件[7]。

图2表示结合部的柔性联接方式，假设结构A为管线，设管线上一个联接点Ax在a方向的振动位移为，受力大小为，同样的，假设结构B为附件，设结构B的其中一个联接点Bs在a方向发生的振动位移为，所受作用力为，由位移相容条件和力平衡条件，其振动位移和作用力满足式（1）。

图2　子结构连接方式

作为柔性对接点的约束条件，式(1)表示管线和附件交界面在载荷作用下的刚度矩阵和阻尼矩阵可以等效为动刚度与KJ相同的一个子结构，该子结构两端与管线和附件联接部位仍然为刚性连接，这样就把管线与附件联接的柔性结合点通过动力特性等效变换为一个子结构和另一个子结构相连接的两个刚性结合点。

2　结合部等效参数修正

根据等效参数建模原理，可以将结合部刚度矩阵作为管线与附件结合部的阻尼和刚度的等效参数，利用现场实测数据对该参数进行修正计算。参数修正方法本质是单目标函数的多变量优化问题，目标函数和修正参数需要通过选择优化算法进行迭代计算以获取最优解[8]。

借助有限元工具Ansys对管线和附件结构进行建模和优化计算，获取接近真实管线系统动力特性的动力修正参数，在此基础上，进行结构动力学分析并提供改进建议将更加准确。文献[5]已经对压缩机管线系统灵敏度进行了分析，管线刚度和位置对管线的模态影响最明显，要还原真实的振动现场，管线位置约束等已经固定，不需要再进行参数识别优化计算，因此只需要将结合部刚度作为待定参数进行计算。

结构动力学模型修正基础是迭代算法，通常采用使数值计算和测试结果残差向量的加权和最小化方法来修改结构参数。通常目标函数表示为

式中εZ为数值计算和测试结果之间的初始残差向量，Wε表示加权系数矩阵，当待修正参数个数少于测试数据量时，最小化目标函数与经典最小二乘估计问题等价；当待修正参数个数大于测试数据量时，最小化目标函数式具有非唯一解。此时，有多组优化刚度可供选择。在进行结构动力修改方案设计时，可根据实际情况选择最优解或次优解。

3　应用实例

3.1往复式压缩机一级出口管线模型

利用有限元分析软件Ansys中参数化编程语言APDL对某石化企业往复式压缩机一级出口管线进行建模仿真。建模时采用管单元以提高建模效率，直管采用Pipe16单元，弯管处采用Pipe18单元，三通管采用Pipe17单元，法兰和阀门对管道系统的作用主要是附加惯性，而对管道系统的弹性影响可忽略，故它们可视为集中附加质量。变径管用两段直径渐变的等质量直管单元代替。

现场实测采用日本理音公司的便携式振动数据采集仪VA-12，对该管道的选取了8个测点的24个方向进行了振动位移、速度、加速度的采集，测点位置图如图3，测试结果见表1。

图3　测点布置图

表1　现场实测结果

根据结合部等效参数动力学建模原理，结合部的阻尼和刚度可以用等效刚度表示，由于该管道有四个约束，与容器相连接的管道为焊接，因此该形式的连接设置为X、Y、Z三个方向的刚度，管夹S-Q2根据现场约束状态只考虑X向的刚度参数等效，而Y向不限制自由度，Z向为固定约束。设置目标函数主要考虑该管段的最大位移值，根据前文所述，测试参数小于待修正参数时，最小化目标函数式具有非唯一解，最终将求得多个优化刚度。将多个优化刚度代入原模型中，即利用结构动力修改的正问题进行结构模态特性的重分析，若得出的模态和振型与测试结果一致性较好，则说明优化刚度可近似真实刚度值；若与测试结果不符合，则选取其他刚度结果进行重分析。现详细介绍求解过程。

3.2结合部等效参数求解

采用结构动态特性响应优化算法可求解结合部等效参数。文献[9]指出，结构动态响应优化计算时需要较高的收敛性，为克服结构动态响应分析计算量大、迭代速度受限的缺点，尝试采用Ansys优化算法中的零阶算法粗算求解目标函数范围，最后结合1阶算法对优化参数进行精确计算。优化设计中的目标函数、设计变量和约束条件定义如下：

(1)目标函数

结构动力响应优化问题计算量巨大，不可能把所有频率下的最大位移响应值都作为计算对象，在实际的优化计算中只是选取了激振频率（10 Hz）前6阶倍频下的最大位移值，作为目标函数，即

(2)设计变量

根据压缩机一级出口管的结合部约束有缓冲罐V 202/3、缓冲罐V 202/4、换热器E 202和支架S-Q2，容器结合部有三个方向弹性约束，管夹有一个方向弹性约束，设计变量表示如下

(3)约束条件

根据一级出口管线的实际分布情况和振动规范，确定约束条件如下

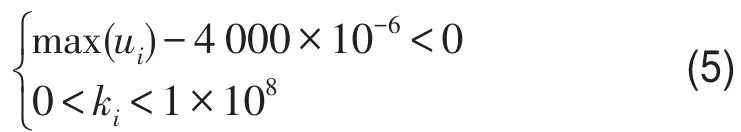
(4)优化求解

根据前文所建模型，采用APDL编程进行优化计算，在算法上综合零阶方法和1阶方法的优点，采用零阶方法中的随机法和子问题法确定最优值的大体位置，然后用1阶方法进行精确求解。经过迭代计算最终求得23组优化值，代入验证，得出与测试结果最接近的一组刚度值。表2为一级出口管线系统动力特性优化的结果，优化程序中定义刚度值变化范围为1×10-8～1×108N/m。图4为该组等效参数对应管线在20 Hz激振频率下动力响应图。

表2　一级出口管动力特性优化等效参数值

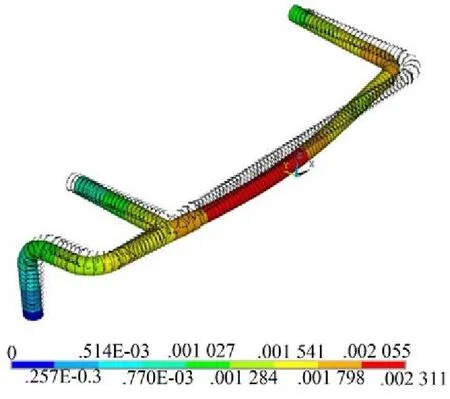
图4　采用等效参数时管线动力响应图

优化后，目标函数从2 354 μm变化为2 311 μm，降低了43 μm，误差为1.8 %。这是因为实际上结合面的动力特性是非线性的，但是在数值仿真时将其作为线性处理，同时结合面的等效方法及刚度、阻尼值本身就存在误差。在模型优化时，还要考虑振型因素，因此不能完全按照使目标函数值最小来处理，当精度要求过高时，二者几乎不可调和[10]。模拟与实测最大位移值误差较小，说明通过优化管线等效刚度参数可很好地还原真实振动现场。

3.3使用等效参数前后固有频率分析

对使用等效参数优化之后的一级出口管线系统进行模态特性分析，得到前20阶固有频率，现与使用非弹性约束管线系统的固有频率相对比，对比结果如表3所示。

表3　等效参数优化前后的固有频率对比表/(Hz)

由表3对比可知，使用等效参数优化之前管线系统的固有频率较高，与现场实测在10 Hz、20 Hz被激发产生较大位移不符。使用等效参数优化之后的管线系统固有频率较低，第5阶固有频率为20.044 Hz，容易被激振频率的2倍频激发产生共振，这也与现场实测20 Hz下位移值达到2 354 μm相符合。说明使用结合部等效参数模型更能接近真实的振动现场，表3结果还说明管线系统固有频率偏低，第5阶固有频率落在了激发频率2倍频的共振区间是导致管道产生剧烈振动的原因。该管系的振动位移值已经超过了美国普渡压缩机协会规定的危险值1 780 μm，因此急需对管系进行改造，控制振动值在合理范围。

3.4管道系统结构改进

针对管道剧烈振动的解决方案，可以着眼于改变刚度、质量、阻尼或者所受的激发力，工业现场的工况及管道布置方式等已经确定，最切实可行的方案是通过改变管夹的约束形式、位置、数量等来调整管道的刚度[11]。刚度值大小可类比前文所述优化过程进行改造，但在设计变量中需定义管夹位置及管夹两个方向的刚度；在约束条件中需要定义管夹位置变化范围。由于最终要将振动位移降低到美国普渡压缩机协会规定的设计界限250 μm以下，因此经过迭代试算，此时目标函数定义为最大位移值接近150 μm，最后结合零阶算法和1阶算法进行管道与新管夹结合部刚度值和位置的优化计算，所确定管夹添加位置和刚度值如图5所示。

图5　新添加管夹位置图

弹性管夹如图6所示，施工安装图如图7所示。

图6　管夹三维模型图

图7　管夹安装图

两个管夹中其中一个距离缓冲罐V 202/4出口法兰1.785 m，X向弹性约束刚度值9.68×106N/m，Z向弹性约束刚度5.81×107N/m。另外一个距离缓冲罐V202/3出口法兰0.669 m，X向弹性约束刚度值为3.84×107N/m，Z向弹性约束刚度5.96×107N/m。现场采用碟形弹簧进行弹性约束，这是因为碟形弹簧刚度大，缓冲吸振能力强，能以小变形承受大载荷，适合于轴向空间要求小的场合，同时具有变刚度特性，对同样的碟形弹簧采取叠合时，弹簧数越多刚度越大，采取对合时，弹簧数越多刚度越小，因此该弹簧的刚度特性可在很大的范围内变化。碟形弹簧示意图如图8所示。

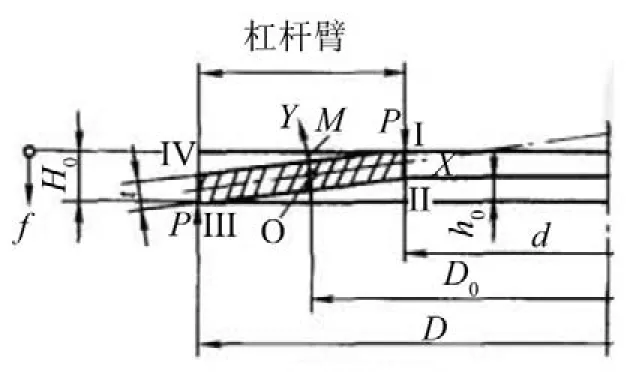
图8　无支承面碟形弹簧

碟形弹簧刚度计算公式为

其中

f——单片碟形弹簧变形量，mm；

E——弹性模量，MPa；

μ——泊松比；

t——碟簧厚度，mm；

K4=1（无支承面）；

D——碟簧外径，mm；

d——碟簧内径，mm；

h0——碟形弹簧压平时变形量计算值，mm；

通过同种碟形弹簧叠合或对合的组合安装方式，可以接近所需的优化刚度值，安装时通过调整锁紧螺母扭转角度可使刚度值更加接近。经过计算，管夹S-Q21处X方向（水平向）需要两片碟簧对合，安装扭转角度46.7°，Z方向（竖直向）需要6片叠合，安装扭转角度11°，S-Q22处采取同种方法。对结构重新进行模态分析得到改造后固有频率见表4。

表4　改造后管系前10阶固有频率

从表4可以看出，改造后系统固有频率与原系统相比有所提高，避开了原来引发剧烈振动的固有频率20.044 Hz。同时对管道进行谐响应分析。结果显示，优化改造后的系统在10 Hz激振频率下产生最大位移，最大振动位移为109 μm，比原位移2 354 μm下降了2 245 μm，减振幅度达到了95.4 %，振型如图9所示。

图9　优化后10 Hz激励下动力响应图

4　结语

（1）通过结合现场实测数据和Ansys中的优化算法，可以模拟计算出管道与附件结合部等效刚度参数，还原真实的振动现场。

（2）将结合部等效参数应用到结构动力修改中去，可以对管道结构系统进行优化，使其避开共振频率，得到满足要求的动力响应值。

参考文献：

[1]胡于进，李俊，李立.平面联接固定结合部动力学模型的一种建模方法[J].计算机与数字工程，2012，6(40)：1-3.

[2]章罡本，彭学院. CAESAR在往复压缩机管道振动及应力分析中的应用[J].化工设备与管道，2007，44(1)：38-41.

[3]徐斌，邹清波，余小玲，等.有限元方法数值模拟往复压缩机管路的振动[J].压缩机技术，2009，(6)：6-8.

[4]薛玮飞，杨晓祥.往复压缩机管道振动有限元法分析[J].福建化工，2002，(4)：56-61.

[5]赵杰，李峰，刘录.基于有限元的超高压管线系统振动特性灵敏度分析[J].振动与冲击，2014，33(10)：148-151.

[6]廖伯瑜，周新民，尹志宏.现代机械动力学及其工程应用[M].北京：机械工业出版社，2004.

[7]南江，杨灿宇，周新民.结合部等效参数修改在结构动力分析中的应用[J].西南林学院学报，2006，26(3)：62-66.

[8]芮强，王红岩，欧阳华江.机械结构动力学模型修正技术的现状与发展[J].装甲兵工程学院学报，2012，26(2)：1-8.

[9]李峰.超高压压缩机及其管线系统的振动控制研究[D].北京：中国石油大学机械设计及理论系，2012.

[10]郭成龙，袁军堂，李奎.基于结合面参数的整机动态特性分析与试验研究[J].机械设计与制造，2012，(2)：149-151.

[11]李峰，王德国，刘录，等.超高压压缩机及管线系统的振动分析与控制[J].中国机械工程，21，(6)：656-659.

Application of Equivalent Parameters of Joints in Vibration Control of a Reciprocating Compressor Pipeline

WANG Ying , ZHAO Jie , LIU Lu , LI Feng , YUAN Wei
（Collegeof Mechanical Engineering, Beijing Instituteof Petrochemical Technology, Beijing 102617, China）

Abstract:In order to solve the problem of vibration in a large reciprocating compressor unit and its pipeline, an effective numerical computation model was established. In this model, the pipeline vibration characteristic analysis method based on the finite element analysis was combined with the dynamic modification technology based on the equivalent parameter. The joint part of the pipeline and the accessory was treated as an elastic constraint, and its optimal equivalent stiffness was calculated. Then, the real vibration model was restored. Based on modal analysis of the real model combined with thefield measurement data, thecauseof pipelinevibration wasidentified. Then, using thetechnology of theequivalent parameter identification, a retrofit scheme for the pipeline was put forward. The improved pipeline could avoid the resonancefrequency and thevibration amplitudewasreduced by 95.4%. Thismethod hasimportant guiding significancefor establishingtheeffectivenumerical model for practical engineering.

Key words:vibrationandwave; finiteelement; equivalent stiffness; dynamicmodification; joints; elasticconstraint

作者简介：王莹（1989-），男，硕士研究生，主要研究方向为振动与噪声控制。E-mail:wangyingmaster@bipt.edu.cn

基金项目：北京市自然科学基金资助项目（3132013）；北京市大学生科研训练项目（2014X00037）；北京市促进人才培养综合改革项目（14010221047）

收稿日期：2015-03-24

文章编号：1006-1355(2016)02-0209-06

中图分类号：TH45

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.046