运载火箭无滚控装置的制导控制技术研究

郭振西，谢 佳，王 颖，闵昌万

（空间物理重点实验室，北京，100076）

运载火箭无滚控装置的制导控制技术研究

郭振西，谢 佳，王 颖，闵昌万

（空间物理重点实验室，北京，100076）

取消滚控装置可简化火箭系统方案，增加质量比，提高火箭运载能力，有效降低成本。分析运载火箭的惯性耦合和运动耦合机理，给出无滚动控制状态下，滚动角的非线性运动方程与相平面分析结果。对无滚控装置的火箭，通过解耦制导控制技术实现姿态稳定和制导目标。以无滚控装置的单推力矢量喷管固体火箭为背景，通过六自由度仿真分析，验证了解耦制导控制技术的可行性。

运载火箭；自由滚动；解耦控制；制导控制

0 引 言

运载火箭经常采用摆动发动机控制推力矢量的方向，产生控制力，达到控制俯仰、偏航和滚动姿态角的目的。多喷管发动机一般采用中心对称的排列布置方式，发动机喷管的摆动方向不同可产生相应的俯仰力矩、偏航力矩和滚动力矩[1]。但对于单喷管发动机，由于其推力中心在运载火箭的轴线上，发动机喷管的摆动只能产生俯仰和偏航力矩。传统的单喷管发动机运载火箭三轴稳定制导控制方案是在运载火箭上加装滚控装置。滚控装置可以采用游动推力发动机、固体滚控发动机或滚控喷管。加装滚控装置会增加系统的复杂性，同时也会减小运载器的有效载荷。

在小型空地导弹中，为了简化导弹控制系统的设计，常采用自由滚动弹体设计，即通过俯仰偏航控制实现导弹的制导任务，滚动通道只进行稳定，而不进行控制[2]。近年来，有文献对大型火箭滚转的运动机理进行了研究[3～5]，大多集中在主动滚转的机理和方法上。随着捷联惯组的广泛使用，惯性元器件对全姿态飞行的适应能力越来越强，运载器无滚动控制的技术方案已经从制导和控制测量上排除了障碍。如果火箭滚动角速度在无控状态下不超出惯性导航系统的测量范围，同时不超过发动机喷管的切向摆动速度，则可以保证箭体在俯仰和偏航方向的控制稳定性。本文给出了运载火箭自由滚动状态下的制导控制动力学模型以及采用自由滚动方案的限制条件，最后以固体火箭为例，分析箭体自由滚动的运动模式，按照自由滚动状态设计相应的制导控制律，并进行了六自由度仿真验证。

1 自由滚动箭体的运动模型

把火箭看作可操纵的变质量物体在空间运动，则可建立如下数学方程[6]。

动力学方程：

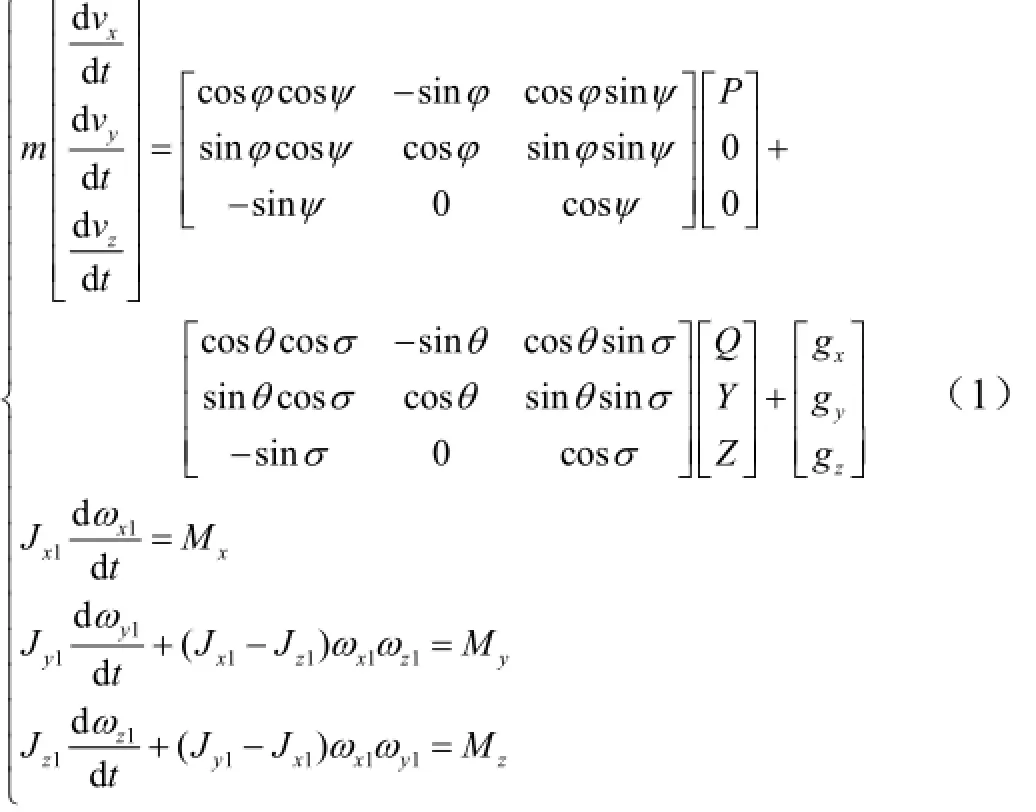
式中 m，θ，σ分别为火箭的瞬时质量、弹道倾角、弹道偏角；ψ，φ分别为火箭的偏航角、俯仰角；P，Q，Y，Z分别为发动机推力、导弹气动阻力、升力、侧力；1xJ，1yJ，1zJ分别为绕箭体坐标系3个轴的转动惯量；xM，yM，zM分别为外力矩在箭体坐标系3个轴上的分量；1xω，1yω，1zω分别为火箭角速度在弹体坐标系上的投影；xv，yv，zv分别为箭体在发射坐标系的速度；xg，yg，zg分别为重力在发射坐标系下的分量。

运动学方程：

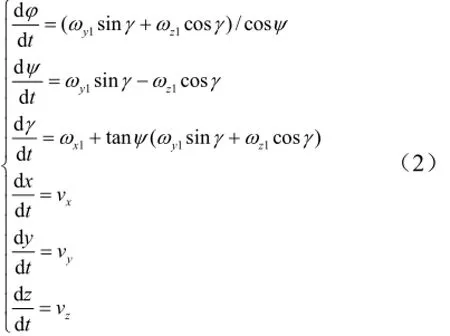
式中 γ为滚动角。

几何关系式方程：

式中 α，β，ν分别为火箭的攻角、侧滑角和倾侧角。

2 制导控制方程解耦

对于滚动自由的运载火箭，建立如下箭体坐标系和准箭体坐标系：

a）箭体坐标系B（-o xyzb）：箭体坐标系B的原点位于火箭质心，且与箭体固连，oxb轴与箭体纵轴重合指向端头，oyb轴位于运载火箭纵轴对称面内，ozb轴构成右手坐标系。

b）准箭体坐标系B＇（-o x y z′′′）：准箭体坐标系B＇的原点位于火箭质心，且与箭体固连，'ox轴与oxb轴重合，'oy轴垂直'ox轴并位于运载火箭的射面内，oz'轴和'ox，'oy构成右手坐标系。此坐标系不随箭体绕oxb轴旋转。

运载火箭助推段制导采用程序角跟踪+横法向导引的制导方案；姿态控制采用俯仰程序角和偏航程序角稳定控制。为消除箭体滚动对制导任务和制导目标的影响，将制导和控制方程建立在准箭体坐标系下。

制导方程：

式中 Uφ为纵向导引系数；Uψ为横向导引系数；dΘ为当地弹道倾角偏差；dH为高度偏差；dψ为弹道偏角偏差；dZ为横向位置偏差；1K，2K，3K，4K分别为制导系统的设计增益。

姿控方程：

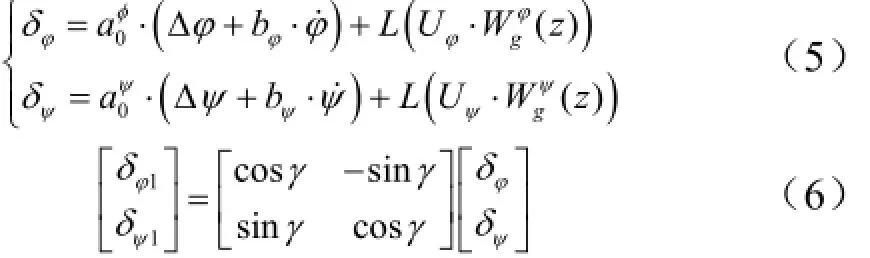
00φψ

Wφ，Wψ分别为制导滤波网络。

gg

3 自由滚动控制能力分析

3.1 滚动角运动模态

在自由滚动模式下，火箭滚动角运动的主要干扰来自于质心横移、发动机推力横移以及气动力矩的零次项偏差。当偏航角为小角度时，近似有γ˙=ωx1，建立简化的滚动角的运动模型如下：

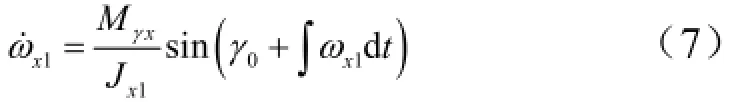
式中xMγ为滚动通道的最大干扰力矩；1xω为滚动角速度；0γ为最大干扰力矩在滚动方向的投影角度的初始值。式（7）为非线性微分方程，采用相平面法分析[7]方法，得到结果如图1～4所示。

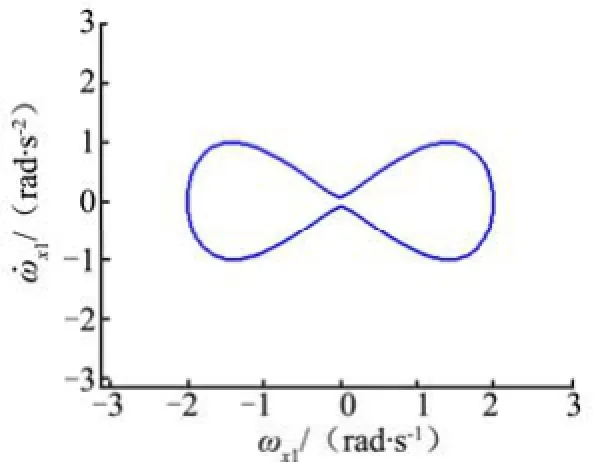
图1 05γ=˚时1xω的相轨迹

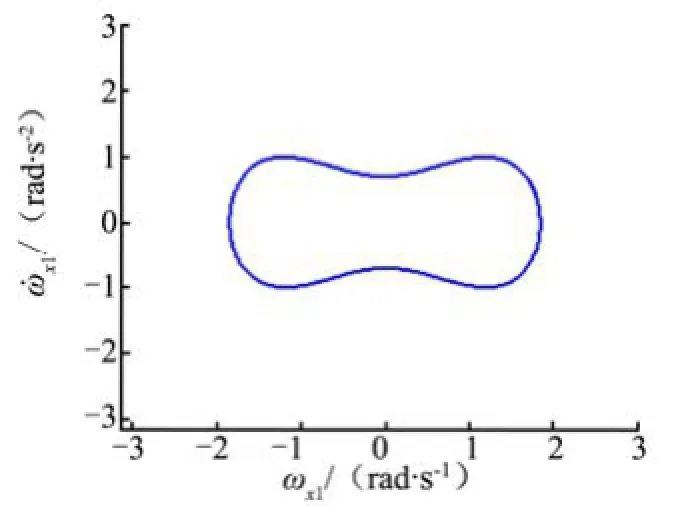
图2 045γ=˚时1xω的相轨迹

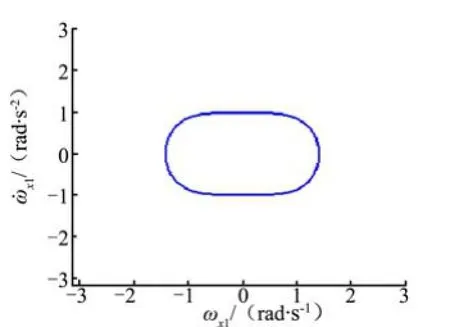
图3 090γ=˚时1xω的相轨迹

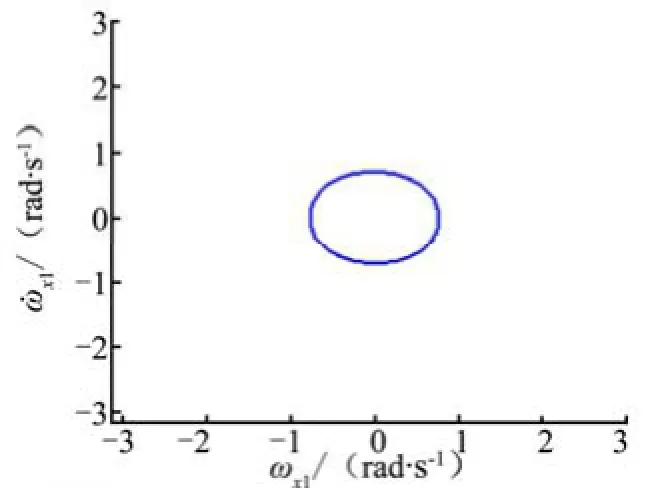
图4 0135γ=˚时1xω的相轨迹

由图1～4可以看出，在自由滚动模式下，随干扰力矩的初始投影角度大小不同，1xω处于不同的稳定极限环上。总体来说，滚动角速度为稳定的振荡状态。

3.2 惯性耦合影响分析

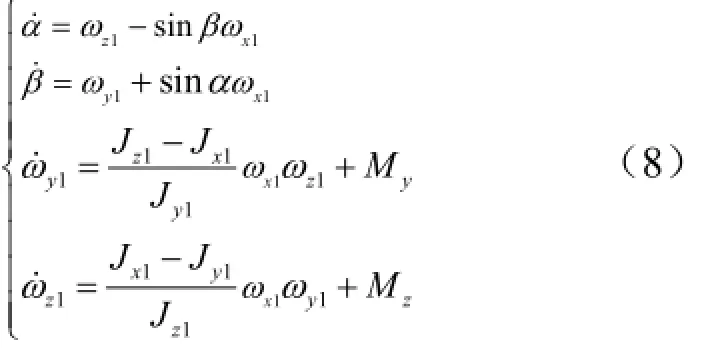
式（9）的特征方程为

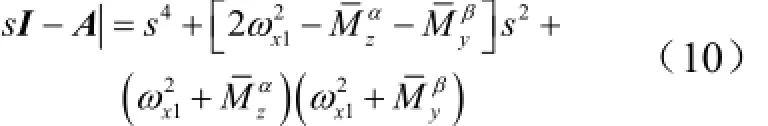
式中Mα

z为俯仰力矩系数对攻角的导数；Mβy为偏航力矩系数对侧滑角的导数。

系统稳定的条件为(ωx

2

1+Mα

z)(ωx

2

1+Mβy)＞0，对于轴对称飞行器即只要满足式（11）的条件，即可保证飞行器在自由滚动模态下稳定。式中 ωnφ为俯仰通道闭环控制系统的自然角频率，；ωnψ为偏航通道闭环控制系统的自然角频率，

3.3 运动耦合影响分析

对于三轴稳定的助推段低弹道方案，运载器通常采用负攻角下压飞行。如果采用自由滚动模式，运载器的实际飞行攻角和侧滑角会随滚动角的变化周期变化，即产生所谓的运动耦合影响：

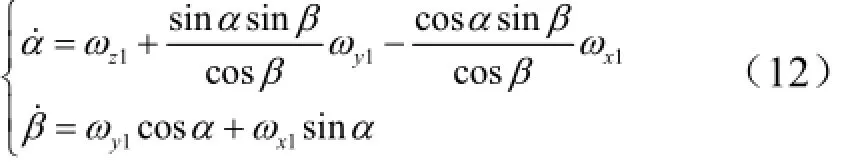
考虑到攻角和侧滑角为小角度，式（12）可以简化为

式中cxα为程序攻角；cxδ为程序摆角；maxδ为喷管最大摆角；δ˙为喷管角需求角速度。

4 仿真分析

4.1 运动特性分析

以固体运载火箭为例开展仿真分析，火箭为轴对称外形。为保证交班点的低高度任务要求，在准箭体坐标系下，弹道采用二次负攻角下压方案。设计结果如图5～8所示。

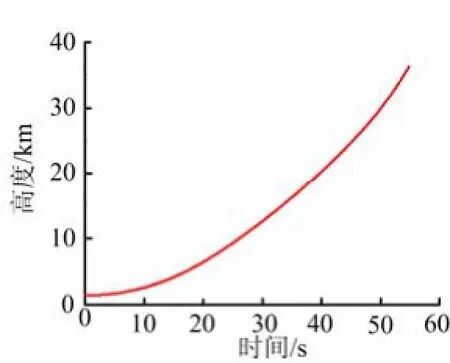
图5 时间-高度特性曲线

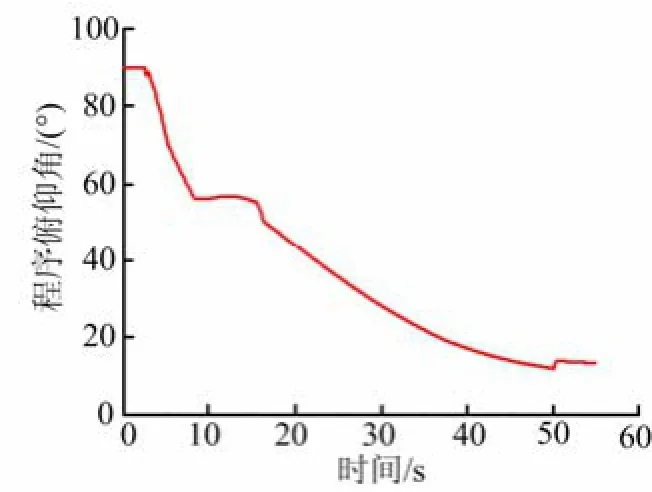
图6 时间-程序俯仰角特性曲线

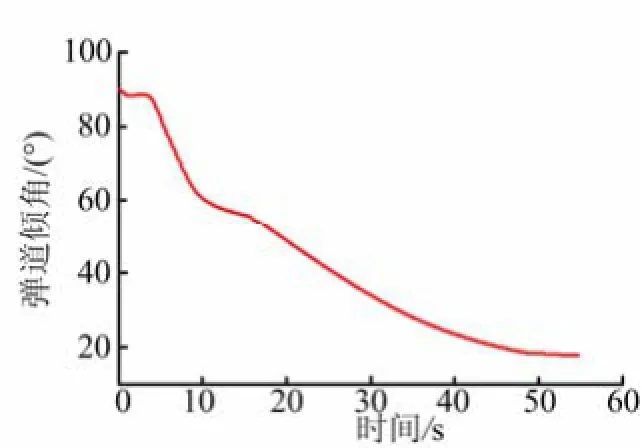
图7 时间-当地弹道倾角特性曲线

由计算分析得到滚动角运动模态的最大干扰力矩为2 000 N·m，滚动方向的转动惯量为800 N·m2。根据式（7），得到最大滚动角速度ωx1max≈114（°）/s；根据式（11），取一定的安全系数，设计俯仰、偏航通道的闭环控制动态特性ωnφ(ωnψ)＞3ωx1max=6 rad/s；按照式（14），在喷管的最大摆角δmax≈8°时，得到对喷管摆速度需求≤16（°）/s。

4.2 六自由度仿真结果

按照4.1节分析的结果，设计了滚动自由的主动段制导和姿态控制律，并在Simulink环境下进行了六自由度仿真。结果如图9～14所示。

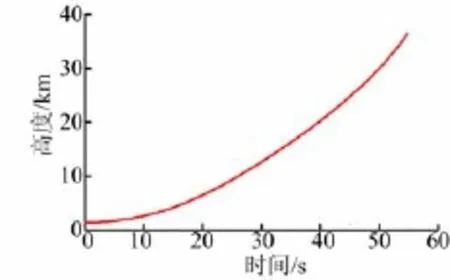
图9 飞行时间-高度仿真曲线

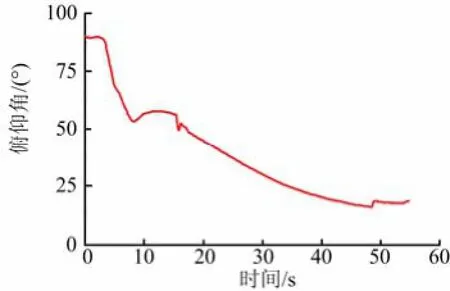
图10 飞行时间-俯仰角仿真曲线

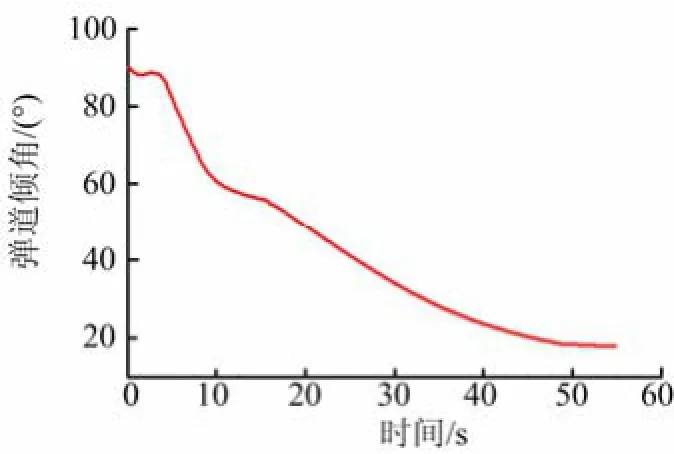
图11 飞行时间-当地弹道倾角仿真曲线

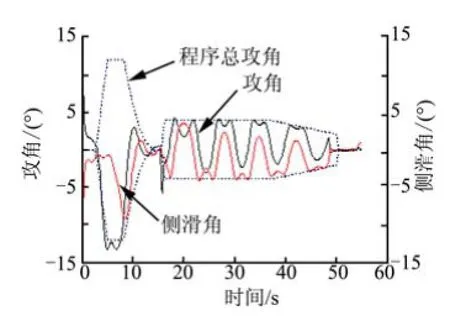
图12 飞行时间-攻角和侧滑角仿真曲线

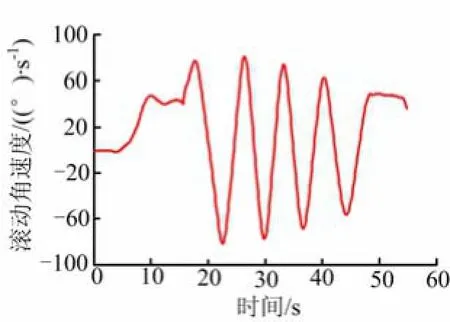
图13 飞行时间-滚动角速度仿真曲线

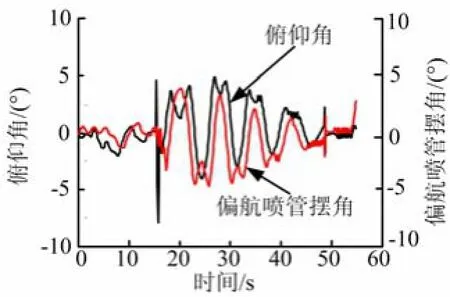
图14 飞行时间-俯仰、偏航喷管摆角仿真曲线

由图9～14可以看出，在自由滚动模式下，滚动角速度稳定振荡；相应的攻角和侧滑角在设计的程序攻角包络内交互变化；俯仰、偏航喷管的摆角大小也随滚动角变化，制导和控制目标均达到预期，这一现象与前面章节分析的结论一致。

5 结 论

本文提出一种取消运载火箭滚动控制装置的制导控制技术方案。从飞行器的滚动角运动模态、惯性耦合、运动耦合特性出发，利用非线性相平面方法，分析了取消滚动控制装置的基本条件，提出一种通过软件解耦的制导控制方法。最后通过数学仿真分析证明了此制导控制技术方案的有效性。

此项研究意义在于：a）利用软件解耦技术，取消运载火箭的滚动控制硬件装置，简化系统方案，提高火箭运载能力，降低火箭成本；b）给出了运载火箭能够采用无滚动控制装置的设计边界条件，可以供方案设计初期参考。

[1] 徐延万. 控制系统（上）[M]. 北京: 中国宇航出版社, 2005.

[2] 彭冠一. 防空导弹武器制导控制系统设计[M]. 北京: 中国宇航出版社, 1994.

[3] 郑新, 傅维贤, 赵民. 滚转弹道导弹运动规律与控制研究综述[J]. 航天控制, 2011(01): 93-98.

[4] 刘君, 孟云鹤, 程伟民, 汤国建, 陈克俊. 滚转弹道导弹耦合特性研究[J]. 弹箭与制导学报, 2011 (01): 5-9.

[5] 郭景录, 马忠文, 王志. 低速滚转弹道导弹的鲁棒滑模控制[J]. 火力与指挥控制, 2008 (09): 71-74.

[6] 程国采. 弹道导弹弹道学[M]. 北京: 国防科技大学出版社,1999

[7] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2001.

[8] 比施根斯. 超声速飞机空气动力学和飞行力学[M]. 上海: 上海交通大学出版社, 2009.

Research on Guidance and Control Technology Used by Rocket’s Free Rolling Applicance

Guo Zhen-xi, Xie Jia, Wang Ying, Min chang-wan
(Science and Technology on Space physics Laboratory, Beijing 100076)

Removing rolling appliance is able to simplify rocket’s system concept，raise the mass ratio, enhance vehicle’s payload and decrease the cost effectively. Inertial and kinematic coupling mechanism is analyzed and the nonlinear kinematic equation and phase-plane results of rolling angle are given under free rolling condition. The decoupling guidance and control technology enables free rolling rockets to achieve attitude stability and guidance goals. The 6 dOF simulation analysis of single thrust vector solid rocket verifies the feasibility of decoupling guidance and control technology.

Rocket; Free rolling; decoupling control; Guidance and control

V448

a

1004-7182(2016)01-0061-05

10.7654/j.issn.1004-7182.20160114

2015-09-17；

2015-11-10

郭振西（1976-），男，高级工程师，主要从事飞行器导航、制导与控制技术研究