基于末级钝化推力变轨的月球借力轨道设计

李重远，王建明，周天帅，何兆伟，朱冬阁

（北京宇航系统工程研究所，北京，100076）

基于末级钝化推力变轨的月球借力轨道设计

李重远，王建明，周天帅，何兆伟，朱冬阁

（北京宇航系统工程研究所，北京，100076）

对于运载火箭发射探月返回飞行试验器任务，火箭末级会跟随试验器再入返回地球，因其再入速度快、落区散布范围广，存在严重的安全隐患。为解决末级再入带来的安全性问题，提出基于末级钝化推力变轨的月球借力轨道设计方法，使末级进入绕地月飞行的大椭圆轨道。利用钝化推力实现月球引力辅助变轨，进而达到优化绕地月飞行轨道近地点高度的目的。

探月返回；火箭末级；再入地球；钝化推力；月球借力；轨道设计

0 引 言

运载火箭发射探月返回飞行试验器，器箭分离时火箭末级与试验器具有相同的轨道根数，绕月飞行后最终再入返回地球。由于器箭分离后的火箭末级轨道机动能力有限，导致末级再入地球时落区散布范围很广，并且火箭末级再入速度快，再入过程往往无法完全烧毁，给末级残骸的落点预报和安全防护带来极大困难。

本文设计了末级月球借力机动轨道，利用末级排放剩余能量产生的钝化推力进行轨道机动，从而接近月球实施月球引力的借力，使末级进入绕地月飞行稳定轨道，规避了末级再入地球带来的安全性问题。

1 月球借力轨道设计方法

1.1 总体思路

基于钝化变轨的月球借力轨道设计的总体思路：迭代末级飞行程序角，在兼顾器箭远场安全性的基础上，利用钝化推力进行轨道机动接近月球，进而实施月球引力的借力。月球借力轨道设计关系如图1所示。

图1 月球借力轨道设计关系图

由图1可以看出，i∞V，o∞V，ΔV，plV，iV，oV的矢量关系。月球公转速度Vpl与Vi和Vo的夹角分别用αi和αo表示。进入月球引力影响球之后，考虑局部二体问题，末级将以双曲线轨道近距离接近并离开月球。由于月球引力为保守力，末级飞越前后入射及出射双曲线超速大小完全相等，方向发生偏转。一般来讲，Vpl，Vi和Vo并不共面，除非Vpl在V∞o和V∞i确定的平面内，大多数初步分析中可以进行类似的假设。

1.2 设计过程

以月球影响球为边界，通过入口点B和出口点c（B和c均为末级轨道与月球影响球的交点）进行月球借力轨道设计，如图2所示。

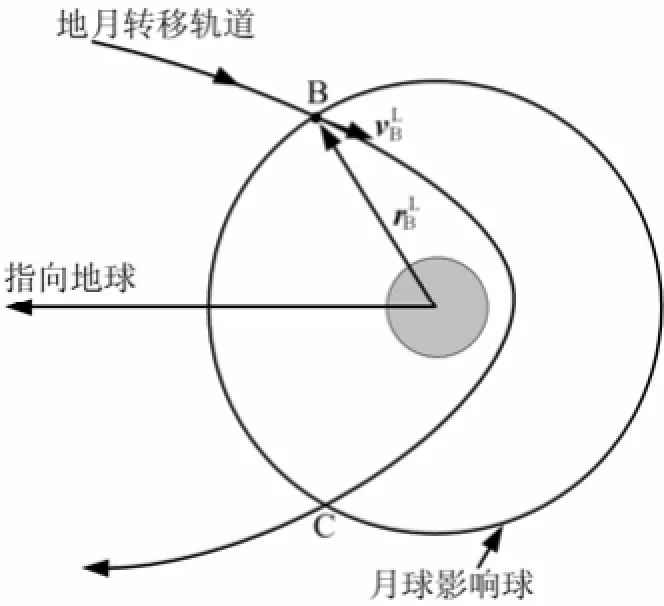
图2 月球借力轨道设计示意

给定入口点B的经度、纬度和到达入口点时刻（用于计算月球位置），则由式（1）和式（2）即可得到入口点B相对于地心的位置和速度矢量，完成月球借力轨道设计。

基于末级钝化推力变轨的月球借力轨道设计方法实施过程如图3所示。

图3 实施过程示意

1.3 摄动因素

对于地月转移轨道和月地转移轨道，摄动轨道动力学方程为

式中 R，V分别为飞船相对于地心惯性坐标系的位置矢量和速度矢量；ea为地球非球形摄动加速度；Sa为太阳引力摄动加速度；Ma为月球引力摄动加速度；Ra为太阳光压摄动加速度；ta为小推力加速度；oa为包括大气阻力、地球反照辐射压摄动等引起的其它加速度。

2 月球借力轨道设计效果

按上述方法设计，钝化结束时末级地月转移轨道远地点高度约371 000 km，末级绕地月稳定轨道第1周期近地点高度可达210 000 km，如图4所示。

图4 末级与试验器和月球轨道关系

由图4可以看出，试验器绕月后进入月地转移轨道，直接再入地球，而经过钝化变轨后的末级，借助月球引力，很好地抬高了近地点高度，进入了绕地月稳定运行的轨道。

以STK软件预估末级轨道寿命，如图5所示。

图5 末级轨道寿命估算

由图5可知，器箭分离后轨道半长轴有增大趋势，基于STK分析，末级短时间内不会再入返回地球。

3 月球借力轨道对主要偏差适应能力

影响末级再入的主要偏差包括：±30%钝化推力偏差、±6 600 km器箭分离时远地点高度偏差。下面就两类极限工况进行分析。

a）钝化推力偏差-30%，aHΔ=+6 600 km。

该工况将导致钝化结束时末级地月转移轨道远地点高度为385 000 km，末级绕地月稳定轨道第1周期近地点高度可达97 000 km，如图6所示。

图6 末级轨道示意

以STK软件预估末级轨道寿命，如图7所示。

图7 末级轨道寿命估算

由图7可知，器箭分离后轨道半长轴有增大趋势，基于STK分析，末级短时间内不会再入返回地球。

b）钝化推力偏差+30%，aHΔ=－6 600 km。

该工况将导致钝化结束时末级地月转移轨道远地点高度为359 000 km，末级绕地月稳定轨道第1周期近地点高度可达62 000 km，如图8所示。

图8 末级轨道示意

以STK软件预估末级轨道寿命，如图9所示。

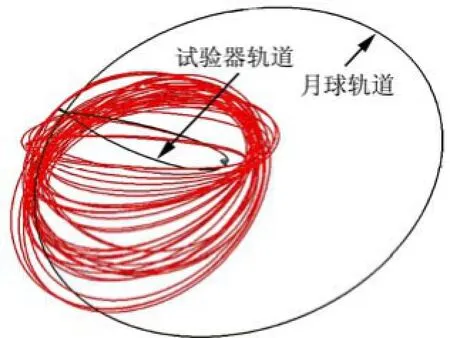
图9 末级轨道寿命估算

由图9可知，器箭分离后轨道半长轴有增大趋势，基于STK分析，末级短时间内不会再入返回地球。

综上所述，基于钝化变轨的月球借力轨道设计方案，能够适应主要偏差的影响，保证末级短时间内不会再入返回地球。

4 远场安全性分析

4.1 考虑的主要误差因素及其组合方式

在进行远场安全性分析过程中考虑的误差因素主要包括以下几点：a）±30%末级箭体钝化排放推力偏差；b）±5%器箭相对分离速度偏差；c）±200 kg末级箭体质量偏差；d）±45%末级箭体冷氦排气推力偏差。

将上述误差因素进行不同的组合，计算具有代表性的偏差弹道，用于分析器箭分离后试验器与火箭末级的最小与最大相对距离。标准相对距离计算中不考虑任何偏差。具体的偏差组合方式见表1。

表1 典型轨道的偏差项组合

4.2 钝化情况下器箭远场计算情况

器箭远场安全性分析计算到试验器再入地球。钝化情况下器箭远场计算情况如图10、图11所示，均以器箭分离时刻为时间零秒。

图10 钝化情况下器箭远场计算结果（＜3000 s）

图11 钝化情况下器箭远场计算结果

由图10、图11可知，器箭远场距离逐渐加大。器箭分离后，按设计程序角进行推进剂钝化排放，以及借助月球引力实施轨道机动，都不会影响试验器安全。

5 结束语

利用末级排放剩余能量产生的钝化推力进行轨道机动接近月球来实施月球引力借力的轨道设计方法，在确保试验器安全的基础上，使火箭末级进入绕地月飞行的大椭圆稳定轨道，解决了末级再入返回地球带来的安全性问题，同时也达到了火箭末级钝化减缓空间碎片的目的，为探月工程的完成发挥了重要作用。

[1] 辛晓生, 侯锡云, 刘林. 地月系L_1点的月球借力间接转移轨道设计[J].飞行器测控学报, 2014, 33(1): 65-70.

[2] 张洪波, 曾亮. 一种跳跃式返回再入的预测—校正制导方法[J]. 飞行器测控学报, 2014, 33(1): 82-87.

[3] 汤敏兰, 刘赟. 离轨段回归轨道设计[J]. 航天控制, 2013(6): 62-65.

[4] 郭敏文, 王大轶. 基于改进Gauss伪谱法的探月返回器跳跃式再入轨迹优化设计[J]. 航天控制, 2013, 31(4): 31-37.

[5] 左光, 侯砚泽, 陈冲, 郭斌. 载人航天器月地返回再入问题研究[J]. 航天器工程, 2013(6): 112-118.

[6] 李小玉. 深空借力飞行/小推力轨道设计与优化[d]. 北京: 中国科学院研究生院, 2010.

Study on the Moon-gravity Assisted Trajectory design Utilizing Passivated-thrust of Final Stage of Launch Vehicle Maneuver

Li Zhong-yuan, Wang Jian-ming, Zhou Tian-shuai, He Zhao-wei, Zhu dong-ge (Beijing Institute of aerospace Systems engineering, Beijing, 100076)

In the lunar flyby-return missions, the final stage of launch vehicle should goes with lunar exploration spacecraft and return to earth, which brings serious security concerns for its ultra-high re-entering speed and ultra-wide falling region. Herein, the development on the large ellipse orbiting-earth trajectory design is studied. The security problem of final stage of vehicle in the reentry process is solved. passivated-thrust maneuver is adopted in the Moon-gravity assisted trajectory design, and the altitude of the perigee of the orbiting-earth is optimized.

Lunar return; Final stage of launch vehicle; Re-entry earth; passivated-thrust; Lunar gravity assist; Trajectory design

V412.4+1

a

2015-04-03；

2015-06-19

李重远（1985-），男，工程师，主要研究方向为弹道设计