基于单轴连续旋转调制的方位对准技术

赵晓伟，李 江，党 宁，白焕旭，邓志宝

（1. 北京航天发射技术研究所，北京，100076；2. 中国兵器工业集团202研究所，西安，712000）

基于单轴连续旋转调制的方位对准技术

赵晓伟1，李 江2，党 宁2，白焕旭1，邓志宝1

（1. 北京航天发射技术研究所，北京，100076；2. 中国兵器工业集团202研究所，西安，712000）

捷联惯组冷态启动、环境温度变化、长时间未标定都可能使陀螺常值漂移发生变化，进而影响捷联惯组的方位对准精度。为减小陀螺常值漂移对方位对准精度的影响，进行基于单轴连续旋转调制的方位对准技术研究。通过理论分析可知，转台单轴连续旋转条件下，将陀螺常值漂移周期性调制，陀螺常值漂移对方位对准精度影响较小，转台转速越高，对准时间越长，方位对准收敛振荡幅值越小，收敛速度越快。通过算法仿真和试验验证了理论分析的正确性。

单轴连续旋转；方位对准；陀螺常值漂移

0 引 言

定位瞄准系统作为武器系统的重要单元，为武器系统提供高精度的射前初始方位角和行进过程中的实时位置信息。捷联惯组作为定位瞄准系统的核心组成部分，其方位对准精度直接决定定位瞄准系统的瞄准精度。一般来说，捷联惯组的方位对准精度受陀螺常值漂移的影响，捷联惯组冷态启动、环境温度变化、长时间未标定都可能使陀螺常值漂移发生变化，进而影响捷联惯组的方位对准精度。为解决上述问题，可对捷联惯组增加转位机构，采用单轴连续旋转的方式对陀螺常值漂移进行周期性调制，进而提高捷联惯组的方位对准精度。文献[1]在罗经法对准频率特性分析的基础上提出一种适于旋转调制捷联惯导系统的罗经对准方法；文献[2]针对光纤捷联惯组在单轴连续旋转条件下进行了方位对准研究，但没有研究单轴连续旋转条件下转速和对准时间对方位对准精度的影响。本文研究了激光捷联惯组在单轴连续旋转条件下陀螺常值零偏、转台转速和对准时间对方位对准精度的影响，并进行了仿真和实验验证。

1 理论分析

1.1 捷联惯组方位对准误差模型

在东北天坐标系下对方位对准误差模型进行推导。

静态条件下，用矢量形式表示陀螺测出的关于IMU坐标系中x，y，z轴的角速率，其量值为地球角速率在每个坐标轴上的分量与陀螺零偏之和，如式（1）所示。

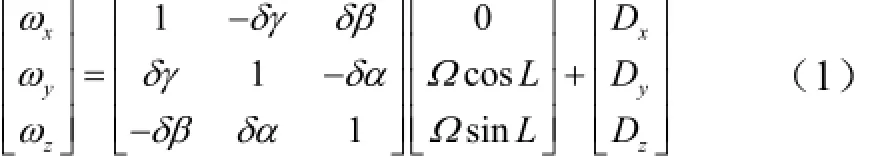
式中 δα，δβ，δγ分别为关于地理坐标系的东向、北向和垂直向的失准；L为当地地理纬度；Ω为地球自转角速度；xd，yd，zd分别为等效东向、北向和天向陀螺零偏。

方位对准过程可以理解为将测量的角速率东向轴分量调零的过程，即：

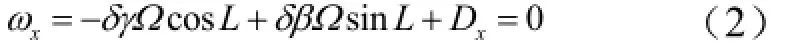
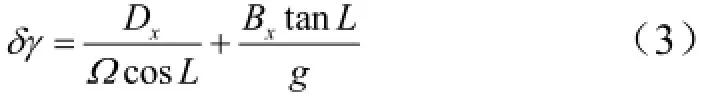
式中 δγ为方位角误差；xB为等效东向加速度计零偏。

1.2 单轴连续旋转状态下方位对准误差分析

在单轴连续旋转过程中，假设IMU坐标系p与旋转坐标系r重合[3]，xε，yε，zε分别为x，y，z轴3只陀螺的常值漂移；e1ε为3只陀螺常值漂移引起的等效东向陀螺常值漂移。转台绕方位轴以角速率ω进行连续旋转，旋转时间为t。3只陀螺常值漂移的等效东向陀螺常值漂移为

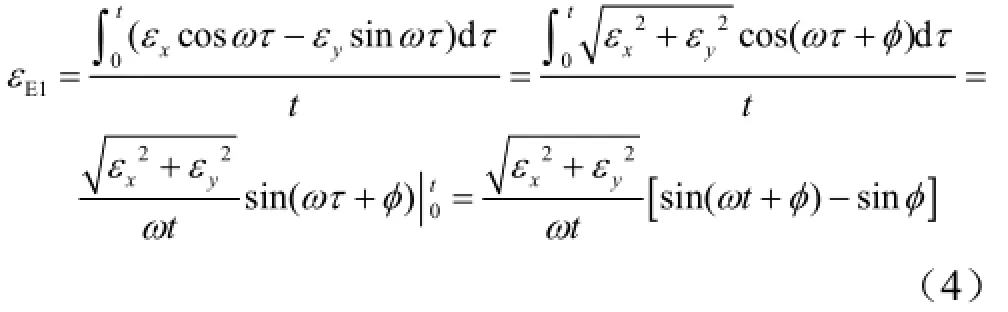
3只陀螺常值漂移引起的方位对准误差为

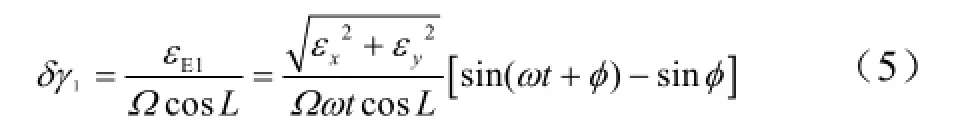
由式（5）可知，单轴连续旋转条件下，方位对准精度与水平陀螺精度、转台旋转速度、初始对准时间和工作地理纬度有关。水平方向陀螺精度越高，转台旋转速度越快，地理纬度越低，方位对准误差衰减振荡幅值越小，方位对准精度越高；且方位对准时间越长，方位对准精度越高。

1.3 单轴连续旋转状态下方位对准算法设计

1.3.1 滤波模型的建立

在捷联惯组方位对准过程中，为使捷联惯组的误差方程[4～6]适合卡尔曼滤波模型，将水平加速度计常值漂移和3只陀螺常值漂移扩充为状态变量。此时捷联惯组的状态方程可以写成如下形式：

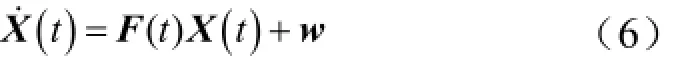
其中，

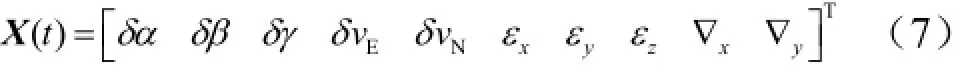
式中 δα,δβ,δγ为姿态误差角；evδ,Nvδ分别为东向、北向速度误差；xε,yε,zε分别为IMU 3个方向的陀螺常值漂移；x∇,y∇为IMU水平方向的加速度计常值漂移。

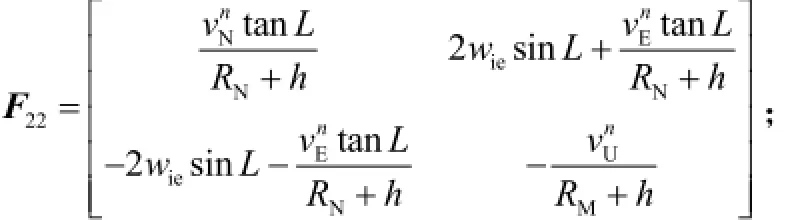
以速度误差作为观测量，设捷联惯组的量测信息为

式中IeIN,vv为捷联惯组解算速度；ReRN,vv为载体真实的速度；eN,vvδδ为速度误差。则，观测方程为

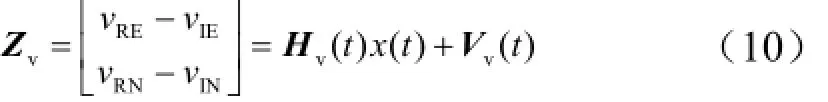
1.3.2 滤波算法

使用Kalman滤波器[7，8]实现方位对准的过程为估计滤波初值的过程。离散状态变量空间表达式如下：

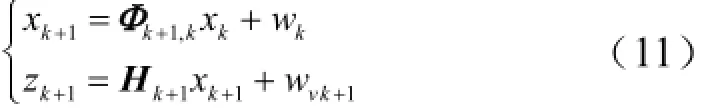
式中 wk,wvk为离散化的零均值白噪声；Φk+1,k为状态转移矩阵；Hk+1为观测矩阵；Qk,Rk分别为wk,wvk的协方差阵。

递推Kalman滤波器包含时间更新过程和测量更新过程如下：

时间更新过程：

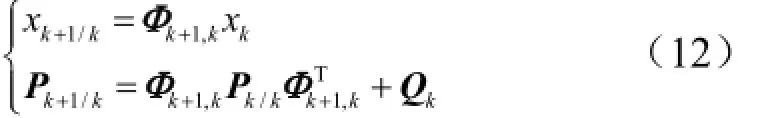
测量更新过程：

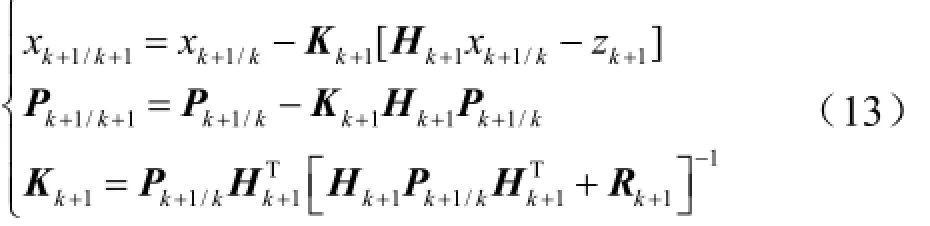
式中1k+K为卡尔曼滤波增益矩阵；1/kk+P为误差协方差矩阵。

每个滤波周期内应用式（12）、式（13）可估计出滤波初值，实现捷联惯组方位对准。

2 单轴连续旋转调制初始对准的仿真与分析

采用MaTLaB对基于单轴连续旋转调制的初始对准算法进行仿真。仿真算法主要由数据源、轨迹发生器、惯性组件误差、对准算法、结果比较5部分组成，图1为基于单轴连续旋转调制的初始对准仿真示意。

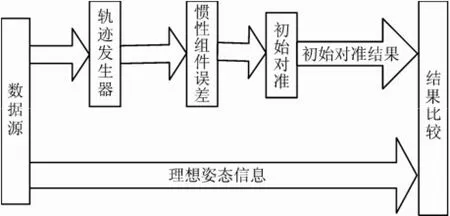
图1 基于单轴连续旋转调制的初始对准仿真示意

a）数据源模块：设定IMU的初始姿态、初始速度、初始位置、IMU转速、转动方案。

b）轨迹发生器模块：根据数据源提供的导航信息，解算IMU坐标系下投影的角速度pipω和比力pipf。该模块是惯性导航解算的逆运算过程，模拟陀螺和加速度计的输出。

c）惯性组件误差模块：根据陀螺和加速度计的误差模型，设置惯性元件的常值漂移、标度因数误差、三轴不正交安装误差、随机噪声误差等误差项。

d）对准算法模块：设计基于单轴连续旋转调制的Kalman滤波精对准算法。

e）结果比较模块：将理想的载体横滚、俯仰、方位信息与初始对准得到的横滚、俯仰、方位信息比较分析。

假设捷联惯组完成粗对准后，初始姿态角误差为[10′，10′，5°]，初始速度误差为[0.01，0.01，0.01] m/s，初始位置误差为[10，10，10] m。转台单轴连续旋转条件下，分别设置不同的陀螺常值漂移、不同的对准时间、不同的转速，分析单一变量对方位对准精度的影响。

2.1 陀螺常值漂移对方位对准精度的影响

假设转台转速为3 (°)/s，旋转时间为10 min；初始姿态角（俯仰角、横滚角、方位角）均为0°；初始速度（东向、北向、天向）均为0 m/s；初始位置经度为116.4°e、纬度为39.8°N、高度为60 m。

在上述假设条件下，仿真比较水平陀螺常值漂移均为0.01 (°)/h和水平陀螺常值漂移均为0.05 (°)/h的10 min情况下的方位对准误差，仿真结果如图2所示。

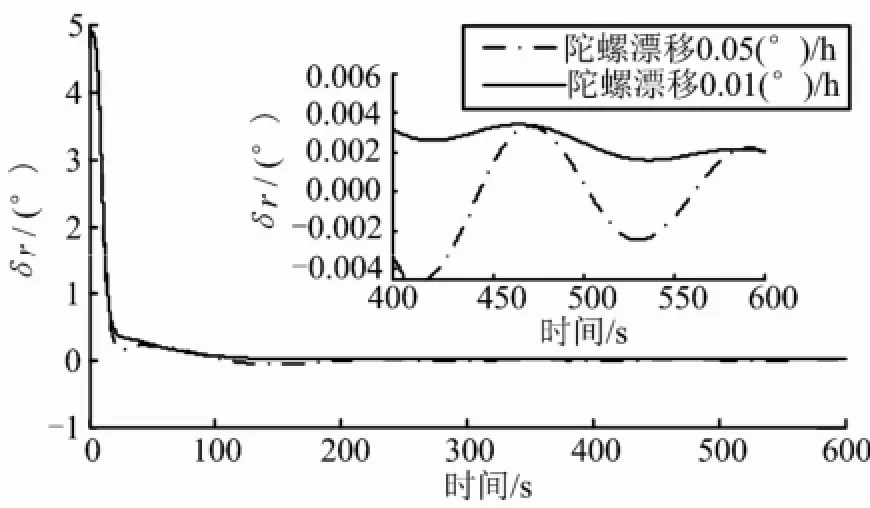
图2 水平陀螺不同常值漂移对方位对准误差影响

由图2可知，不同陀螺常值漂移条件下10 min方位对准误差均小于0.01°。陀螺常值漂移在转台单轴连续旋转条件下不影响方位对准精度。

2.2 对准时间对方位对准精度的影响

假设转台转速为3 (°)/s，旋转时间为20 min；初始姿态角（俯仰角、横滚角、方位角）均为0°；初始速度（东向、北向、天向）均为0 m/s；初始位置经度为116.4°e、纬度为39.8°N、高度为60 m。

模拟实际工况添加惯性组件误差。设置3只陀螺常值漂移均为0.003 (°)/h；3只陀螺随机游走均为0.000 3(°)/；3只加速度计常值漂移均为20 μg；3只加速度计随机游走均为2μg/h；三轴陀螺不正交安装误差均为1″；三轴加速度计不正交安装误差均为5″；3只陀螺和3只加速度计标度因数误差均为1×10-6。

方位对准误差仿真结果如图3所示。

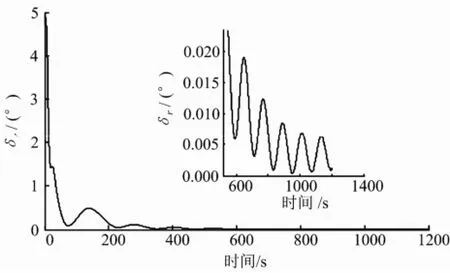
图3 3 (°)/s连续旋转20 min方位对准误差收敛曲线

由图3可知，方位对准在600 s时，方位对准误差为0.006°，在600 s附近，方位对准误差振荡区间为[0.005 9°～0.019°]；方位对准在1 200 s时，方位对准误差为0.001°，在1 200 s附近，振荡区间为[0.006°～0.001°]；仿真结果表明延长对准时间有利于提高方位对准精度。

2.3 不同转速条件对方位对准精度的影响

假设转台转速分别为3 (°)/s、9 (°)/s、18 (°)/s，旋转时间为10 min，初始姿态角（俯仰角、横滚角、方位角）均为0°；初始速度（东向、北向、天向）均为0 m/s；初始位置经度为116.4°、纬度为39.8°N、高度为60 m。

模拟实际工况，添加惯性组件误差。添加误差同第2.2节。不同转速条件下方位对准误差仿真结果如图4所示。

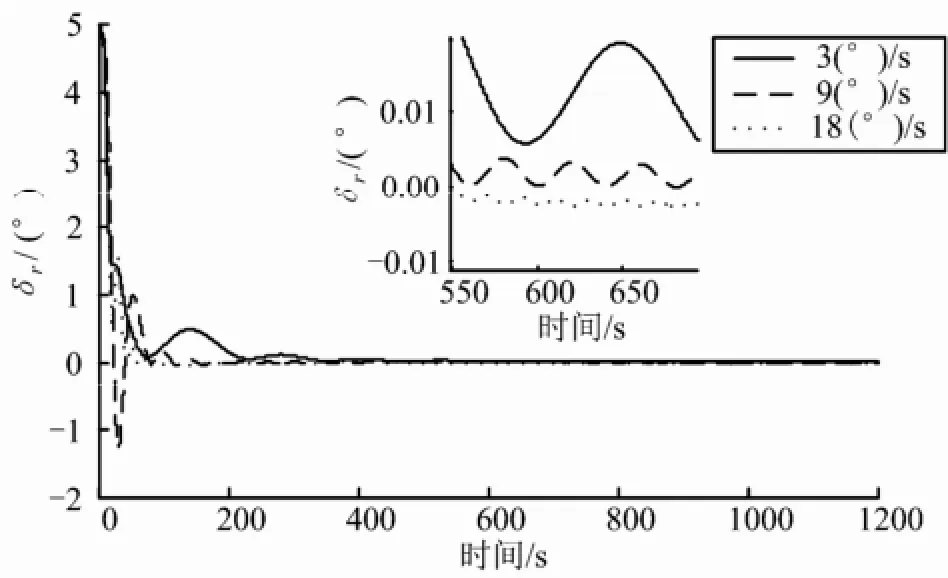
图4 不同转速对方位对准误差的影响

由图4可知，选取对准时间为10 min，3 (°)/s连续旋转对准误差振荡区间在[0.006°，0.019°]；9 (°)/s连续旋转对准误差振荡区间在[-0.002°，0.003°]；18 (°)/s连续旋转对准误差振荡区间在[-0.002°，0.001°]。仿真结果表明：相同的对准时间，转台转速越高，方位对准精度越高，衰减振荡幅值越小。

3 试验验证

在北京（纬度L=39.8°N）、常温（20 ℃）、 实验室（隔离地基）环境条件下进行试验。采用1台6个月未标定的IMU，将IMU固定在高精度三轴转台上，对基于单轴连续旋转调制的初始对准技术进行试验验证。经百秒平滑测试，3只陀螺的零偏稳定性精度分别为0.002 3 (°)/h（1σ）、0.002 6 (°)/h （1σ）和0.002 3 (°)/h（1σ），3只加速度计的零偏稳定性精度分别为9.58 μg（1σ）、15.53 μg（1σ）和13.71 μg（1σ）。对IMU进行纯捷联静态10 min初始对准精度测试，初始对准结果如表1所示。

表1 IMU水平全方位对准结果 单位：(°)

由表1可知，10 min水平全方位对准，方位角对准误差为0.012 6°（45.36″）（1σ）；俯仰角对准误差为0.003 06°（11.02″）（1σ）；横滚角对准误差为0.002 87°（10.35″）（1σ）。

3.1 3 (°)/s单轴连续旋转条件下全方位对准结果

测试过程中，以转台内框、中框、外框读数分别为IMU横滚角、俯仰角、方位角的基准。试验结果如表2～4所示。

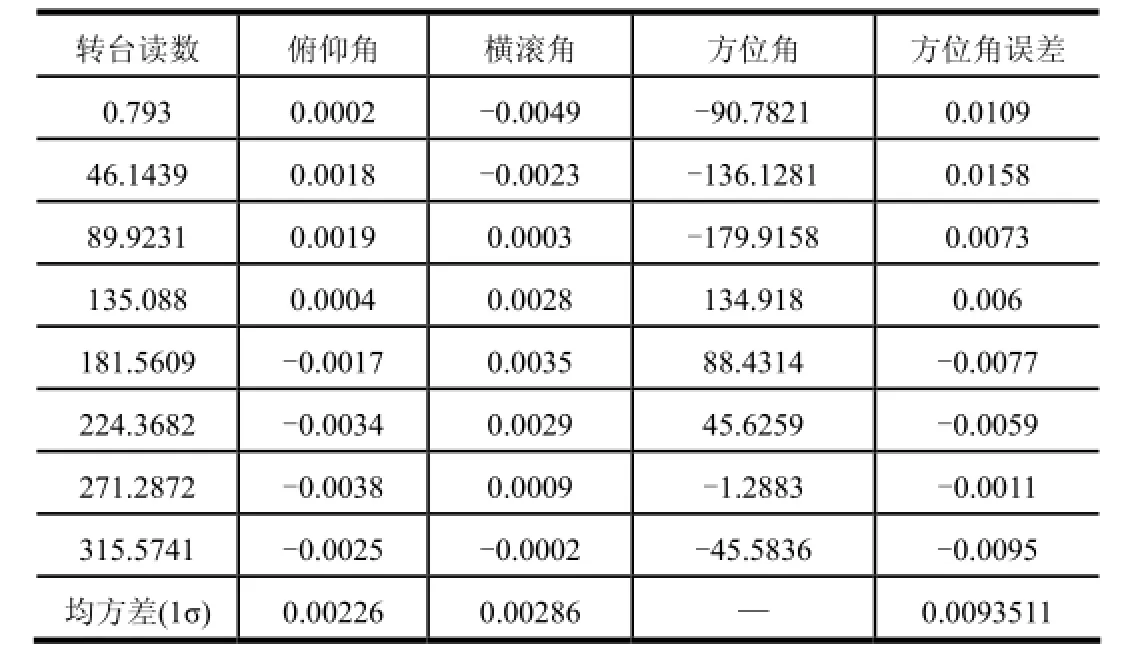
表2 3(°)/s连续旋转10 min水平全方位对准结果 单位：(°)

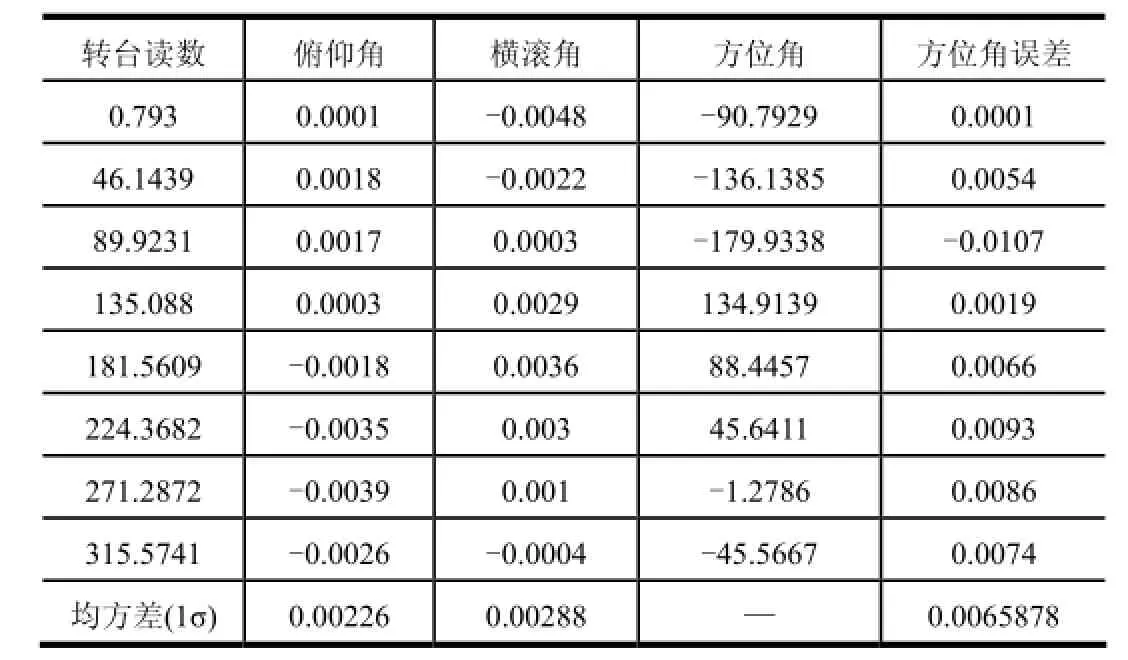
表3 3 (°)/s连续旋转15 min水平全方位对准结果 单位：(°)

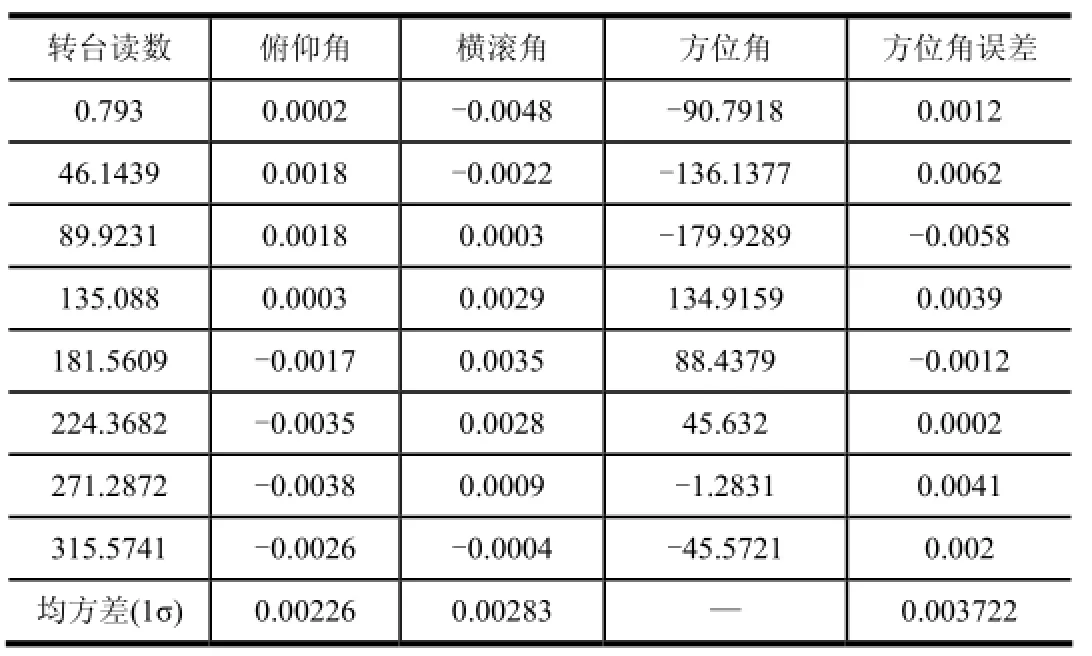
表4 3 (°)/s连续旋转20 min水平全方位对准结果 单位：(°)

由表2～4可知，转台以3 (°)/s连续旋转，当对准时间为10 min，水平全方位对准精度为0.009 4°（33.48″）（1σ）。当对准时间为15 min，水平全方位对准精度为0.006 6°（23.76″）（1σ）。当对准时间为20 min，水平全方位对准精度为0.003 7°（13.32″）（1σ）。随着初始对准时间的延长，方位对准精度将提高。

3.2 10 (°)/s单轴连续旋转条件下全方位对准结果

理论上延长对准时间和提高转速都有利于对准精度的提高，当转台转速为3 (°)/s，对准时间为20 min，水平全方位对准精度为13.32″（1σ）。通过提高转速，期望在更短时间内达到同样的全方位对准精度。

采集了8组以10 (°)/s单轴连续旋转的陀螺和加速度计的有效原始数据，进行离线试验。试验结果如表5～7所示。

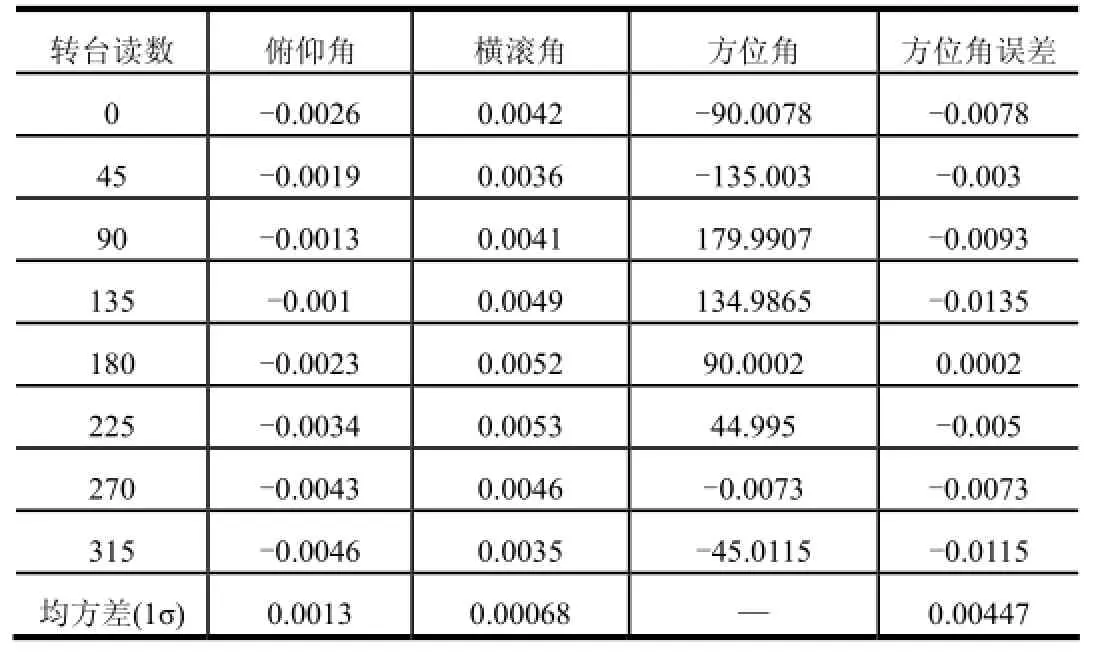
表5 10 (°)/s连续旋转10 min水平全方位对准结果 单位：(°)

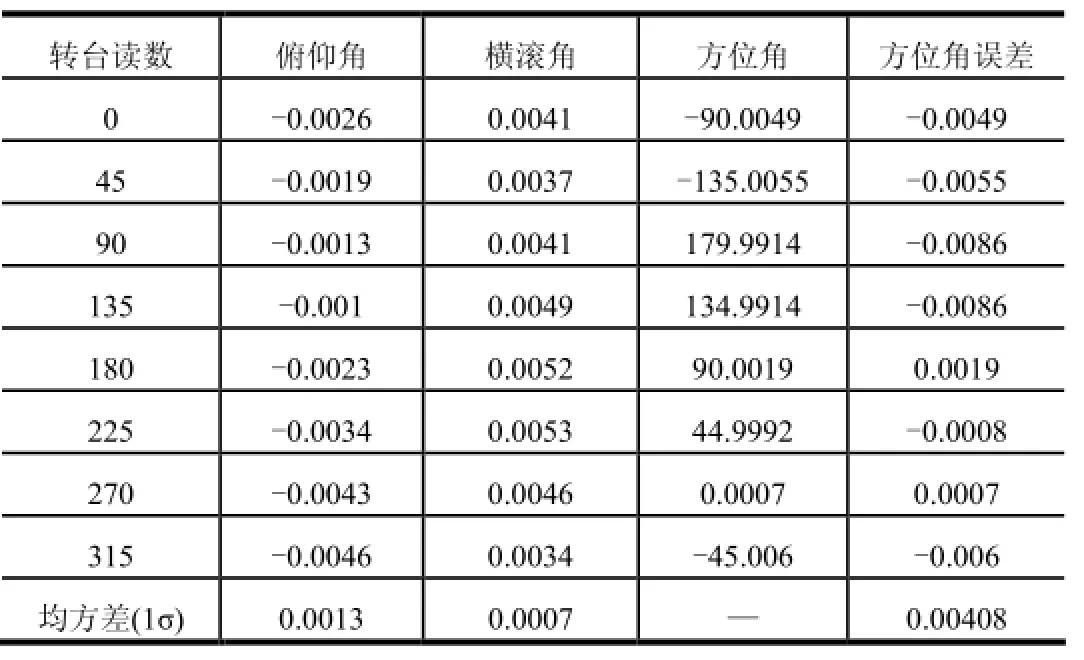
表6 10 (°)/s连续旋转15 min水平全方位对准结果 单位：(°)

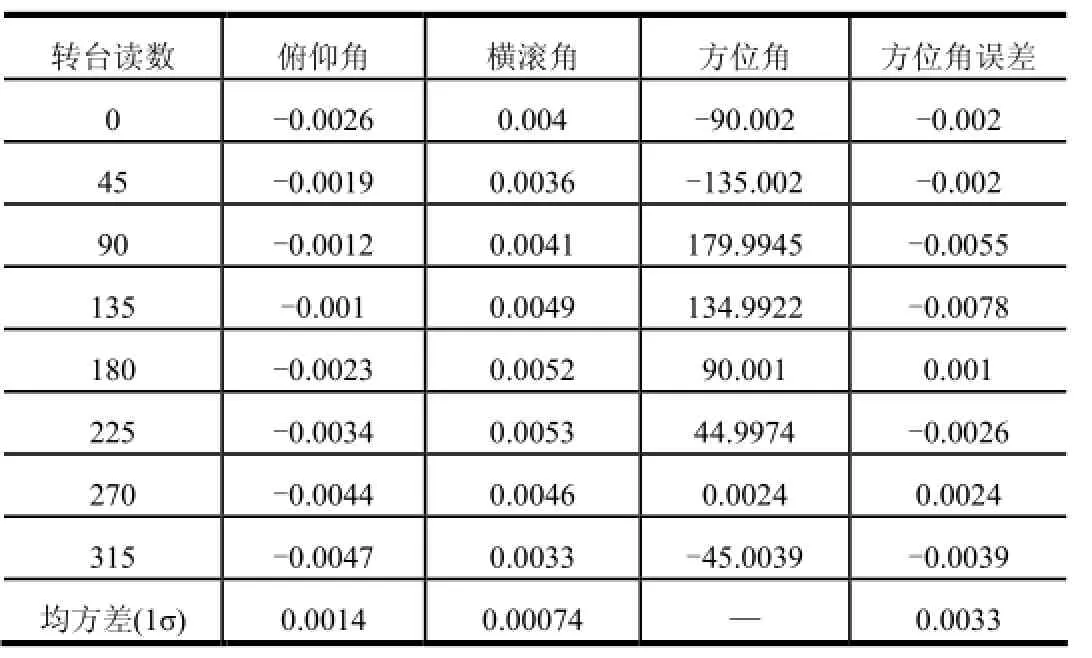
表7 10 (°)/s连续旋转20 min水平全方位对准结果 单位：(°)

由表5～7比较可知，转台以10 (°)/s连续旋转，当对准时间为10 min时，方位对准精度为0.004 47°（16.09″）（1σ）；当对准时间为15 min时，方位对准精度为0.004 08°（14.65″）（1σ）；当对准时间为20 min时，方位对准精度为0.003 3°（12″）（1σ）。转台单轴连续旋转条件下初始对准，初始对准时间越长，方位对准精度越高。

3.3 不同对准时间、不同转速条件下方位对准精度

通过上述试验得到的初始对准结果，比较不同对准时间、不同转速方位对准结果，如表8所示。

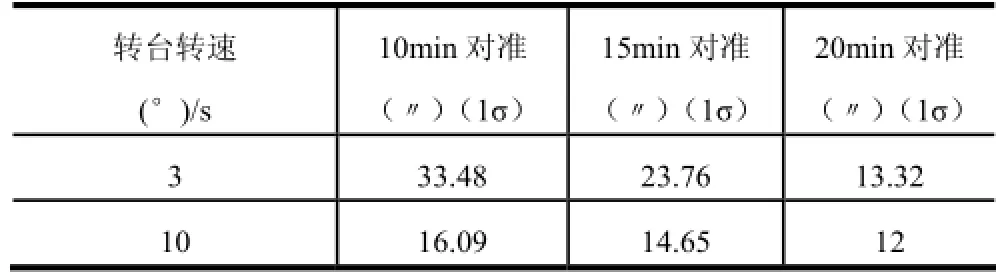
表8 不同对准时间、不同转速方位对准结果

由表8可知，相同的转速，对准时间越长，方位对准精度越高。相同的对准时间，转台转速为10 (°)/s的方位对准精度比转台转速为3 (°)/s的方位对准精度高。但达到20 min时，不同转速条件下方位对准精度相差不大。

4 结 论

在单轴连续旋转条件下，能够将陀螺常值漂移周期性调制，由冷态启动、长时间未标定、环境温度变化引起的陀螺常值漂移不影响方位对准精度。且转台转速越高，初始对准时间越长，全方位对准精度越高。通过算法仿真和试验表明理论分析的正确性和算法的有效性。

[1] 郝燕玲, 张义, 孙枫, 高伟. 单轴旋转式捷联惯导方位对准研究[J]. 仪器仪表学报, 2011, 32(02): 71-77.

[2] 汪滔, 吴文启, 曹聚亮, 郭勇刚. 基于转动的光纤陀螺捷联系统初始对准研究[J]. 压电与声光, 2007, 29(05): 24-27.

[3] 赵晓伟, 孙谦, 陈鸿跃. 单轴旋转捷联惯导系统初始对准误差分析[J].导弹与航天运载技术, 2014(4): 58-62.

[4] 张天光, 王秀萍, 王丽霞. 捷联惯性导航技术（第2版）[M]. 北京: 国防工业出版社, 2010.

[5] 查峰, 许江宁, 黄寨华, 覃方君. 单轴旋转惯导系统旋转性误差分析及补偿[J]. 中国惯性技术学报, 2012, 20(1): 11～17

[6] 袁保伦, 韩松来, 杨建强, 廖丹. 激光陀螺单轴旋转式惯导系统的转动方案分析[J]. 中国惯性技术学报, 2011, 19(2): 145-151.

[7] 龙兴武, 于旭东, 张鹏飞, 等. 激光陀螺单轴旋转惯性导航系统[J]. 中国惯性技术学报, 2010, 18(2): 149-153.

[8] Levinson e, Majure R. accuracy enhancement techniques applied to the marine ring laser inertial navigator(MaRLIN)[J]. Navigation: Journal of the Institute of Navigation, 1987, 34(1): 64-86.

.

Research on Azimuth Alignment Technology Based on the Single Axis Continuous Rotation Modulation

Zhao Xiao-wei, Li Jiang, dang Ning, Bai Huan-xu, deng Zhi-bao
(1. Beijing Institute of Space Launch Technology, Beijing, 100076; 2. No.202 Institute of china Ordnance Industry Group, Xi’an, 712000)

The gyro constant drift was changed by the strapdown inertial measure unit（SIMU）cold start, the change of environmental temperature and uncalibrated for a long time which would also effected the azimuth alignment precision of SIMU. In order to reduce the influence of gyro constant drift to the azimuth alignment precision, the azimuth alignment technology based on the single axis continuous rotation modulation was researched. according to the theory analysis, the gyro constant drift can be periodic modulated under the condition of continuous rotation, so the accuracy of azimuth alignment will be less affected by the gyro constant drift. The higher the rotate speed of turntable was, the longer the alignment time would be, the azimuth alignment convergence oscillation amplitude was smaller and the rate of convergence was faster. The correctness of theoretical analysis was verified through the results of algorithm simulation and test.

Single-axis continuous rotation; alignment of azimuth; Gyro constant drift

V249.3

a

1004-7182(2016)01-0026-06

10.7654/j.issn.1004-7182.20160107

2014-06-03；

2014-07-20

赵晓伟（1988-），男，助理工程师，主要研究方向为航天发射系统惯性导航技术