智能CS算法在分布器设计计算中的应用

冯登科，宋文生，朱　健，李雪冰

(1.辽宁大唐国际阜新煤制天然气有限责任公司，辽宁 阜新　123000；

2.联化科技辽宁阜新天予化工有限公司，辽宁 阜新　123000)



智能CS算法在分布器设计计算中的应用

冯登科1，宋文生1，朱健1，李雪冰2

(1.辽宁大唐国际阜新煤制天然气有限责任公司，辽宁 阜新123000；

2.联化科技辽宁阜新天予化工有限公司，辽宁 阜新123000)

摘要：为了能够更快捷、更高效地设计计算填料塔分布器的结构参数，对分布器的计算模型及变量进行了分析，建立了填料塔分布器计算的数学模型，引入新型智能的布谷鸟演化算法(CS算法)对计算模型进行求解计算；以一个精馏填料塔为实例，计算得到了填料塔分布器结构的参数。结果表明：使用CS算法对分布器进行设计计算是快捷高效的。

关键词：填料塔；分布器设计；演化算法；布谷鸟搜索

随着现代化工分离技术的不断发展和进步，填料塔因其高效、快捷等优点，迅速在分离过程中得到了广泛的应用。分布器和再分布器是填料塔不可缺少的组件，在填料塔中对流体的分布和再分布起着极其重要的作用。在分离过程中填料塔本身对传质、传热效果要求是很高的，很多研究表明[1]，流体的不良分布会导致传质效率的急剧下降。在塔与填料直径比特别大(>40)和特别小(<10)的情况下，流体的不良分布对传质的影响尤为严重[2]。因此，对分布器进行合理的设计计算，以达到均匀合理分布的目的就具有重要的现实意义。

要使流体在分布器上有很好的分布，就必须对多孔管内流体的流动行为进行研究[3-5]，这也是设计计算分布器的理论基础。文献[6,7]在这些理论研究的基础上提出了排管式液体分布器的设计计算方法。但这种计算方法是比较传统的迭代循环调整法，要想找到比较好的设计参数，设计出一个合理、高效的分布器就比较困难，需要经验丰富的工程、设计人员才能实现。

智能演化算法是最近发展十分迅速的一种工程计算方法，又可以称之为随机计算。它的计算原理是借助于自然界生物演化的自然法则，适者生存，不适者被淘汰[8]。智能演化算法种类多种多样，如遗传算法[8]、微粒群优化算法[9]等。这里以一个精馏填料塔管式分布器的设计计算为例，引入一种新型高效的智能演化算法——布谷鸟搜索算法(Cuckoo Search, CS)，来求解分布器的结构参数。经过编程计算，最终快捷高效地得到了相应的计算结果。

1布谷鸟搜索算法

英国剑桥大学的Yang Xin She和Deb Suash在研究了布谷鸟的繁殖行为和莱维(Lévy)飞行特性之后，于2009年创立了布谷鸟搜索算法(Cuckoo Search，CS)[10]，并用大量的函数对其性能进行了测试，结果表明：该算法在许多方面的性能已经超过了遗传算法和微粒群算法[10,11]。CS算法具有全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强等优点[12-14]。

CS算法是基于布谷鸟借窝下蛋的繁殖行为和Lévy飞行机制而演化得到的。布谷鸟将自己的蛋放置在宿主鸟巢里繁殖后代，这个过程同样遵循自然界适者生存的演化规则。而Lévy飞行是法国数学家Lévy提出的描述动物在自然界中随机游走，随机飞行特性的方程，又可以称之为Lévy定律。其幂次形式的概率密度函数可以表示为[10-12]：

Lévy～u=t-λ,(1<λ<3)

这样就可以将Lévy飞行同布谷鸟搜索鸟巢繁衍生息的过程相结合，得到的布谷鸟搜索算法流程见图1。

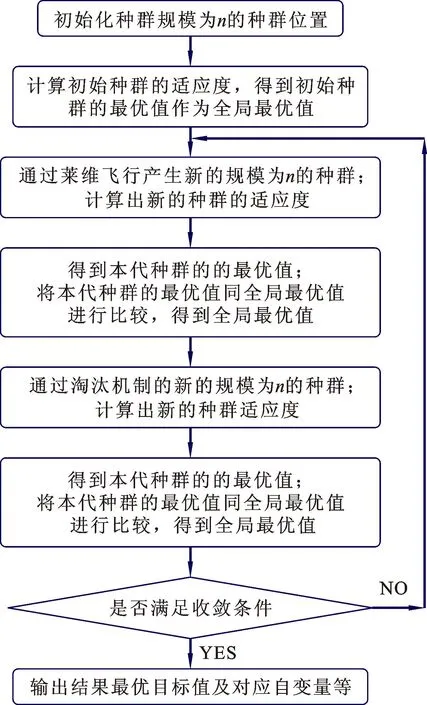
图1　布谷鸟搜索算法流程

2分布器设计计算模型

2.1理论基础

对于一个有n个管孔的多孔管，见图2。设管进口端流体压力为P0，以流体均布为原则，即可假设流体沿各孔口流量相等[6,7]。

图2　多孔分布管示意

多孔管中的气体流动行为多采用修正动量方程描述，其形式为：

(1)

式(1)中，K′称为动量修正系数，p为流体静压，u为主流速度，ρ为流体密度，λ为管道摩擦系数，D为内管径。将式(1)作用于第i孔，并将式(1)的微分方程变换为差分，并做适当变换得管内的压力分布为：

在实际教学中，以统一的分数线作为所有人的目标是不切实的，进步是相对的。因此，教师应引导不同层次的学生制定不同层次的目标，让更多的学生获得自我实现的成就感。

(2)

(3)

式中，ΔPi=Pi-Pa，ΔP0=P0-Pa，P0为管入口处压力，Pa为管外压力，u0为管入口段的流速。

设第i个孔口的穿孔压降为i孔前后管内流体压力的平均值与管外压力之差，即

(4)

穿孔压降与穿孔速度uoi间关系为：

(5)

Ki和ξi无法从理论公式直接计算，其实验关联式为：

(6)

(7a)

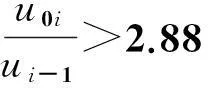
(7b)

2.2目标函数

对于一个有N个孔的分布器而言，以Mf表示分布器的分布均匀程度，其定义为：

(8)

显然，Mf就是要求解的目标函数，Mf越小，表明流体分布越均匀。对文献[1,6,7]中的计算过程进行分析，很明显可以看到，在计算过程中不断调整的变量为自变量，这些变量主要包括穿孔流速、主管和支管管径与长度、喷淋点的布置、孔间距。然而从目标函数Mf可以看出，影响目标函数的变量主要是分布器的孔数N和每个孔的穿孔流量Q0i。N与喷淋点密度有关系，但是对于一类分布器而言，这个值变化范围很小。穿孔流量Q0i与穿孔压降、穿孔流速、主管与支管尺寸等都有关系。然而这些变量之间又有一定的关系，比如穿孔压降与穿孔流速就可以通过式(3-7)进行关联，对这些公式进行变换，就可以得到方程：

f(u0i)=0

(9)

式(9)中：

由式(6,7)可知，Ki和εi均为穿孔流速u0i的单变量函数，这样方程(9)就是穿孔流速u0i的隐函数方程。在求解这个方程时，将式(9)作为目标函数，不断调整变量u0i，只要可以使式(9)的绝对值无限接近于0，就可以认为解出了穿孔流速u0i。这个过程同样可以通过演化算法进行求解计算。将求解得到的u0i回代入式(3)或式(4、5)就可以得到对应的穿孔压力ΔPi。通过这个关系，只要确定自变量穿孔流速u0i，就可以确定穿孔压力ΔPi，两者选一即可。通过这样的分析，最终确定对目标函数Mf影响的主要因素有喷淋点密度Sp、支管数nI、初始穿孔流速u0m、支管管径dI。而支管管径与支管入口流速(即主管对应各支管孔的穿孔流速)有关，这里就选取支管入口流速u0I作为自变量。演化计算时自变量的变化取值范围见表1。

表1　自变量变化范围

3分布器演化计算

对于分布器的计算过程，使用布谷鸟搜索算法对其进行求解，用每一代的布谷鸟个体代表选定的自变量，每个布谷鸟对应的环境适应度表示目标函数，这样就可以智能地对各个变量进行调整，不再像文献[6,7]所述方法那样每次迭代计算都要根据设定的计算公式或者人为地对变量进行调整。而是使用演化算法智能赋值，这样就可以大大提高计算效率。具体的演化计算过程见图3。为了便于比较，使用文献[6,7]所述的分布器设计例子。

图3　分布器演化计算流程

将计算过程流程图3编制成计算机程序，应用VB 6.0的子集Visual Basic For Application 6.0进行编程，在PC(CPU 2.09GHz，内存1.99GB，Window7 32位)运行通过。经过计算可以得到一些好的计算结果值，见表2。

表2　计算结果

经过新型的演化计算就可以得到对应的分布器结构参数的结果，分布器选用2×17个支管对称排布，间距83 mm，每根支管内径为18 mm。喷淋点数为197个，孔间距为145 mm，按照正方形排列，孔径为2.5 mm。主管内径为98 mm，主管正下方开25个孔。计算所得最终的目标函数Mf为0.026 65，这个值比文献[1,6,7]中的值0.075 8要小得多。这里所得的计算结果是合理的，而且更加精确。

4结语

(1)使用布谷鸟演化计算的方法设计计算分布器，得到了分布器的结构参数，所得的目标函数值比文献值更小、更精确，这说明使用演化计算的方法设计分布器是更准确合理的，更能符合均匀分布的准则，是一种新型的分布器设计计算方法。

(2)使用演化计算的方法设计分布器更为智能，计算过程自变量的调节不再使用人为设定的计算公式或人为调节，收敛性更高，这样使得计算过程更快捷、更高效。

(3)这样的演化计算流程可以很好地应用于分布器设计计算。类似计算方法可以在工程实际中得到广泛应用，具有重要的现实意义。

参考文献：

[1] 张明石,余国琮,谭天恩，等.现代塔器技术(第二版)[M].北京：中国石化出版社，2005.

[2] Hope A.Boosting tower performance by more than atrickle[J].Chem Eng, 1985, 92(5):22.

[3] Bassiovny M K, Martin H.Flow distribution and pressure drop in plate heat exchangers I[J], Chem Eng Sci, 1984, 39(4):693.

[4] Senecal V E.Fluid distribution in process equipment[J].Ind Eng Chem, 1957, 49(6):993.

[5] 北京石油化工学院.一种采用气体搅动的填料萃取方法及其所用设备:CN 1316286A[P].2001-10-10.

[6] 董谊仁,过健.填料塔排管式液体分布器的研究和设计[J].化学工程，1990,18(3):28-34.

[7] 董谊仁,裘俊红,陈国标.排管式液体分布器的设计[J].化工生产与技术，1998,5(2):1-5.

[8] K.De Jong.Analysis of the Behaviour of a Class of Genetic Adaptive Systems[D].PhD thesis,University of Michigan,Ann Anbor,1975.

[9] J.Kennedy, R.Eberhart.Particle swarm optimization[C].in:Proc.of the IEEE Int.Conf.on Neural Networks,Piscataway,NJ,pp.1995:1942-1948.

[10] Yang X S. Deb S.Cuckoo Search via Lévy flights[C],in:Proc.of World Congress on Nature & Biologically Inspired Computing(NaBic 2009),IEEE Publications, USA, pp.2009: 210-214.

[11] Yang X S. Deb S.Engineering optimization by cuckoo search[J],Int.J.Math.Modelling & Num.Optimization,2010(1):330-343.

[12] 冯登科,阮奇,杜利敏.二进制布谷鸟搜索算法[J].计算机应用,2013,33(6)：1566-1570.

[13] 姚远远,叶春明.作业车间调度问题的布谷鸟搜索算法求解[J].计算机工程与应用, 2015, 51(5): 255-260.

[14] 李明,曹德欣.混合CS算法的DE算法[J].计算机工程与应用, 2013, 49(9): 57-60.

Application of Intelligent CS Optimization Method in the Design and Calculations of Distributor

FENG Deng-ke1, SONG Wen-sheng1, ZHU Jian1, LI Xue-bing2

(1.LiaoningDatangInternationalFuxinCoal-To-SNGCo.,Ltd.,FuxinLiaoning123000China；2.LianhetechLiaoningFuxinTianyuChemicalIndustryCo.,Ltd.,FuxinLiaoning123000China)

Abstract：In order to design and calculate the structure parameters of distributor in packed column faster and more efficiently, the calculation model and variables of distributor were discussed.And the mathematical model of distributor in packed column was built up.Moreover, the new intelligent nature-inspired optimization method of Cuckoo Search (CS optimization method) was used to solve the mathematical model.Take packing distillation column for an example, its distributor’s parameters were acquired.The results show that using the CS optimization method to calculate distributor is faster and more efficient.

Keywords：packed column; distributor design； nature-inspired optimization method； Cuckoo Search

收稿日期：2015-12-01

中图分类号：TQ 053.5

文献标识码：A

文章编号：1004-8901(2016)02-0009-03

doi：10.3969/j.issn.1004-8901.2016.02.003 10.3969/j.issn.1004-8901.2016.02.003

作者简介：冯登科(1987年-)，男，河南郑州人，2013年毕业于福州大学化学工程专业，硕士，助理工程师，现主要从事化工工艺管理工作。