关于成人微积分教学创新方法的探索*
2016-05-17景海斌邓全才赵丽娟河北建筑工程学院数理系河北张家口075000
景海斌邓全才 赵丽娟河北建筑工程学院数理系,河北 张家口075000
关于成人微积分教学创新方法的探索*
景海斌**邓全才赵丽娟
河北建筑工程学院数理系,河北张家口075000
摘要:成人教育的改革是一个长期而复杂的过程,改革人才培养模式,实现教学内容、手段和方法的创新,提高教育质量,是所有教育工作者奋斗的方向。文章基于成人教育中学员自身的特点和微积分教学的重难点,结合实际教学经验,对成人微积分教学方法进行探索,并提出一些独到有效的方法。
关键词:成人;微积分;教学方法
*本论文为河北建筑工程学院教育教学研究项目:“成人高校数学教学创新模式探索”(项目编号:2013JY2009)研究成果。
在人才竞争日趋激烈的今天,要接受高等教育的观点已深入人心,而作为高等教育中的一员——成人教育得到人们越来越多的认可。众所周知,在自然科学的研究中数学是基础,而微积分则是其它数学课及专业课的基础。所以说微积分的教学效果如何很大程度上影响到高等教育的成败,成人教育也是如此。如何根据成人教育的特点提高数学课的教学质量,就成为成人教育教学改革的重中之重。对于这方面的研究已经有不少专家学者做出了研究,比如刘兴祥就认为应该加大远程教育力度[1];还有学者认为要实现成人高校数学教育创新就要构建全新理念,培养学生创新意识[2]。教学笔者根据自己多年对函授学员的教学经验,来探讨成人微积分教学的几个具体的新方法。
一、培养成人学生对微积分学习的兴趣
兴趣是行动的先导,没有兴趣做任何事情都不会有很高的效率,因此在微积分的学习中首先要做的就是让学生不要有厌烦情绪。根据自己在工作中的经验,对于多数学生来说数学的学习过程枯燥乏味,而这种感觉在成人学员中更为明显,为了能使成人学员对微积分产生兴趣可以采用以下方法:
例如在讲解两个可导函数u(x),ν(x)乘积的导数公式[u(x)ν(x)]'=u'(x)ν(x) + u(x)ν'(x)时,为了激发学员们的兴趣可以这样讲解:假设u(x)和ν(x)是弟兄两个,现在犯了错误,而求导符号“'”表示教训的意思。当父亲教训哥哥时,弟弟在旁边看,当教训弟弟时,哥哥在旁边看[3]。这样学生们就能在轻松的环境下就记住公式,并且领悟到数学的魅力所在。
二、帮助学生养成良好的学习习惯,掌握正确的学习方法
成人学生的基础虽然差,但是理解能力较强,通过教学教会学生如何更好、更快地掌握基本概念对于进一步的学习也是非常重要的。
例如在讲奇函数与偶函数的概念时,书上的定义为“设D为对称于原点的数集,f为定义在D上的函数。若对每一个x∈D有f(-x)=-f(x) (f(-x)=f(x) ),则称f为D上的奇(偶)函数。”这一定义中的难点是表示式不容易记住,而且容易混淆。为了让学生永远记住这一概念,就可以提示学生看到“奇、偶”两字会想到什么?一般学生会回答“奇数和偶数”,但定义中根本看不到奇数和偶数的影子。就可以让学员来看看函数f(x)=xn,其中n为自然数,并推导如下[4]
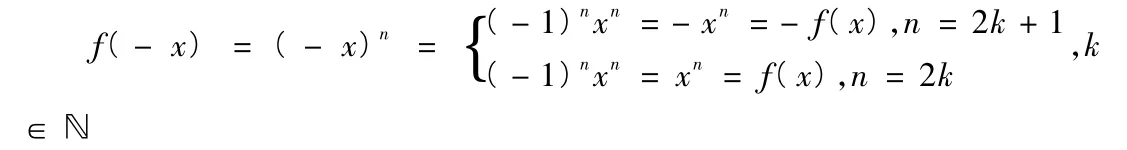
这样学员们不仅对函数的奇偶性更容易记住,而且即使忘了定义,也可简单通过f(x)=xn的性质很容易明白。
三、通过设置情境,让学生对一些易于混淆的概念牢固掌握
关于向量的学习,向量的乘积运算基本的主要有两种:向量的数量积和向量积。数量积()还有另外两种名称叫做“点积”或“内积”;而向量积()也有另外两种名称叫做“叉积”或“外积”。数量积或向量积说明了乘积后的结果为一个数或一个向量,比较好理解,而其他的名称就容易混淆。怎样能把“点积”和“内积”、“叉积”和“外积”更好的对应起来呢?在面授的时候,最好这样给出解释:
假设有一支箭以足够大的力量从屋子的外面射在门上,箭可以穿过门并且留在门上,这时从屋子里面看到的是箭头,是一个点,故称之为内积或点积,若从屋子外面来看,看到的是箭尾像一个叉,故称之为外积或叉积。这样学生们就不会对“内积和外积”到底分别对应的是“点积还是叉积”混淆了。这样就通过形象化的教学方式达到了培养函授学员自主学习能力的目的。
四、注重学员实际动手能力的培养,逐渐提高自信
成人教育的学生一般来说文化基础较差,还有多数学员已参加工作多年,而且课堂时间较少,很大程度上依赖于业余时间。这就要求教学者改变单纯依赖课堂,不分对象,一味讲细、讲全、讲透的满堂灌的教学方法。要根据不同教学对象,采用不同的教学方法才是行之有效的。
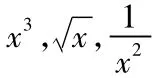
总之,教师应该针对成人学员的实际情况,找到行之有效的教学方法,从而提高学生们学习微积分的积极性,并且培养他们的自学能力。只有这样才能不断推进成人函授教育的健康发展,使学员成为适应新世纪发展要求的高素质人才。
[参考文献]
[1]刘兴祥,赵香萍.成人数学教育专业质量高的策略[J].中国成人教育,2006(9).
[2]宋福庆,朱石焕.成人高校数学教育创新模式探索[J].教育与职业,2006 (21).
[3]叶伟锋.成人高等数学教育创新模式的探索与思考[J].中国科教创新导刊,2009(05).
[4]陈传璋等.数学分析(上)[M].北京:高等教育出版社,1983.
作者简介:**景海斌(1978-),男,河北张家口人,河北建筑工程学院数理系副教授,研究方向:数学教育。
中图分类号:G642.4; O172-4
文献标识码:A
文章编号:1006-0049-(2016)04-0032-01
