Prediction of Ship-Ship Interaction Forces in Shallow Water Using a High-order Panel Method

XU Hu-fu,ZOU Zo-jin,LIU Xio-yn

(a.School of Naval Architecture,Ocean and Civil Engineering;b.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Prediction of Ship-Ship Interaction Forces in Shallow Water Using a High-order Panel Method

XU Hua-fua,b,ZOU Zao-jiana,b,LIU Xiao-yana

(a.School of Naval Architecture,Ocean and Civil Engineering;b.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

A three-dimensional high order panel method based on Non-Uniform Rational B-Spline (NURBS)is developed for predicting the ship-ship hydrodynamic interaction forces during meeting and overtaking in shallow water.A NURBS surface is used to precisely represent the body geometry. Velocity potential on the body surface is described by B-spline after the source density distribution on the boundary surface is determined.A collocation approach is applied to the boundary integral equation discretization.Under the assumption of low passing speed,the effect of free surface elevation is neglected in the numerical calculation,and the infinite image method is used to deal with the finite water depth effect.The time stepping method is used to solve the velocity potential at each time step.The present results of hydrodynamic interaction forces are compared with those obtained by slender body theory and CFD-based RANS method to show the validity of the proposed numerical method.Calculations are conducted for different water depths,lateral distances between ships and ships’speeds,and the detailed results are presented to demonstrate the effects of these factors.The results show that interaction forces are much larger and much more susceptible to water depth,but less susceptible to lateral distance in meeting case than those in overtaking case.

meeting;overtaking;ship-ship hydrodynamic interaction;NURBS; high-order panel method

0 Introduction

Ship-to-ship hydrodynamic interactions involving significant hydrodynamic forces and moments will occur when two ships are moving in close proximity.Particular cases of special interest are the unsteady-state situation of two ships moving in tandem in re-fueling or lighting operation,and situations of two ships meeting or overtaking in restricted water.In each of these cases,hydrodynamic interaction forces and moments may lead to accidents such as collision.

Many previous studies are based on experimental method since it typically produces reliable and realistic results.Vantorre et al(2002)[1]carried out an extensive experimental study onship-to-ship interaction in shallow water involving various ship types.

Theoretical study of ship-ship hydrodynamic interaction was traditionally based on the slender-body theory.Tuck and Newman(1974)[2]extended the slender-body theory to deal with the hydrodynamic interactions between two ships moving with different speed in deep water or with same speed in shallow water.Yeung(1978)[3]undertook theoretical studies on ship-ship hydrodynamic interaction by using the slender-body theory and the method of matched asymptotic expansions.A similar approach was used by Yeung and Tan(1980)[4]to study the hydrodynamic interaction of ships with some fixed obstacles.This study was extended by Hsiung and Gui(1988)[5]to a larger variety of obstacles.In all the studies mentioned above,the free surface effects were ignored under the assumption of low ship speed.

During the last decades,there has also been a growth in numerical study of ship-ship hydrodynamic interaction.Korsmeyer et al(1993)[6]studied the body-to-body interaction in a rectangular canal by using a rectangular Green function.Parallel motion was studied for two spheroids,two Mariner ships and two Panamax bulk-carriers,and comparisons with experimental data showed a fairly good agreement.Yasukawa(2003)[7]derived motion equations for two ships maneuvering in close proximity within potential theory,and simulated the motion of two ferries when one overtakes the other and passes away.A 3D panel method was applied to calculate the added mass and the interaction forces,and the collision caused by the hydrodynamic interaction between ships in shallow water was demonstrated.Xiang and Faltinsen (2010)[8],Zhou et al(2012)[9]carried out the calculation of hydrodynamic interaction forces in restricted waters using potential theory,both encountering and overtaking between target ship and own ship were considered.Sutulo et al(2012)[10]made validation of potential-flow estimation of interaction forces between ships,and affecting factors were analyzed in detail.In all these numerical studies,the free surface effects were ignored.Moreover,all these numerical researches use constant panel method,which is difficult to satisfy the C1-continuity on the body surface.Thus,a high-order panel method is needed.

During the last decades,high-order panel method based on B-spline or Non-Uniform Rational B-spline(NURBS)has been developed rapidly.B-spline and NURBS can provide a more precise description of the body geometry of the ship surface for the purpose of hydrodynamic calculation;moreover,they can be used to represent the source density or velocity potential distribution for potential flow problem,so that the continuity of higher order derivatives of velocity potential on the ship surface can be ensured precisely.Zhang et al(2003)[11]developed a numerical computation method based on B-splines for the hydrodynamic interaction forces between two ships,where the free surface effects were ignored.

In the present paper,a three-dimensional high-order panel method based on NURBS is developed to calculate the ship-to-ship interaction force both in meeting and overtaking conditions.A NURBS surface is used to precisely represent the body geometry.The velocity potential distribution on the body surface is described by B-spline after the source density distribution on the body surface is determined.The collocation method is adopted and the collo-cation points are distributed on the vertices of NURBS surface,and the singularity sources are distributed on the Gaussian points of each panel on the NURBS surface.Under the assumption of low ship speed,the effect of free surface elevation is ignored,and the infinite image method is used to deal with the finite water depth effect.Calculations are carried out for different water depths,lateral distances between ships and ships’speeds to analyze the influences of these factors.

1 Mathematical formulation

We consider two ships moving along parallel courses in proximity of each other,one ship (Ship 1)navigates with a constant speed U1,and another ship(Ship 2)navigates with a constant speed U2,as shown in Fig.1.The coordinate systems o-xyz fixed in the space and oi-xiyizifixed to Ship i(i=1,2)are adopted,where the xi-axis is pointing from ship stern to the bow, yi-axis to port side and zi-axis vertically upward;the oi-xiyiplane coincides with the undisturbed free surface(z=0).The water depth is assumed to be constant and expressed by z=-h. The longitudinal and transverse distances between the ships are denoted by ST and Sp,respectively.

Fig.1 Sketch of ship-to-ship interaction

It is assumed that(1)The fluid is inviscid and the flow is irrotational;(2)The ship speeds are very small,so that the effects of free-surface elevation can be ignored.Furthermore,the shedding of vortices due to viscous effect and flow separation is neglected.The neglect of free-surface effects and shed vortices removes all the memory effects and allows the solution to be stepped through time as a series of independent hydrodynamic calculations(Korsmeyer,et al, 1993)[6].

The perturbation velocity potential representing ship flow is defined as φ（ t,x,y,z）,it satisfies the Laplace equation in the fluid domain and the following boundary conditions:

The velocity potential φ is expressed by source distribution on the hull surfaces as follows:

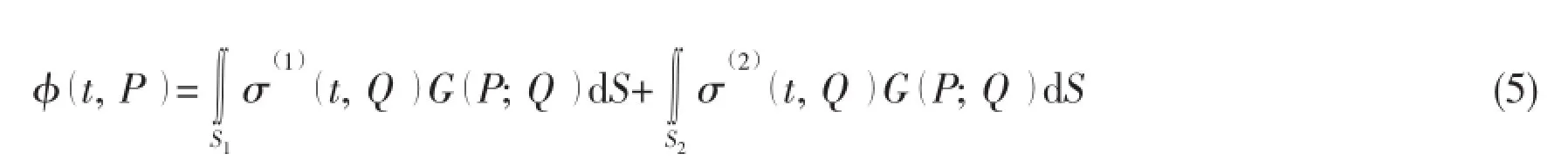
where σ（i）denotes the strength of source distributed on the hull surface of Ship i.P（ x,y,z）is a field point andis a singular point on the surface S which consists of the wetted surfaces S1and S2.The Green function takes the following form:

With application of this Green function formula of infinite mirror-image,the boundary conditions(3)and(4)on the undisturbed free surface and the sea bottom are satisfied automatically;while by satisfying the boundary conditions(1)and(2)on the hull surfaces,it follows the following Fredholm integral equation of second kind:

After Eq.(7)is solved,the disturbance velocity potential and disturbance velocity can be expressed through the density σ by Eq.(5)and Eq.(8):

The pressure distribution on Ship i is determined from the unsteady Bernoulli equationin the following form:

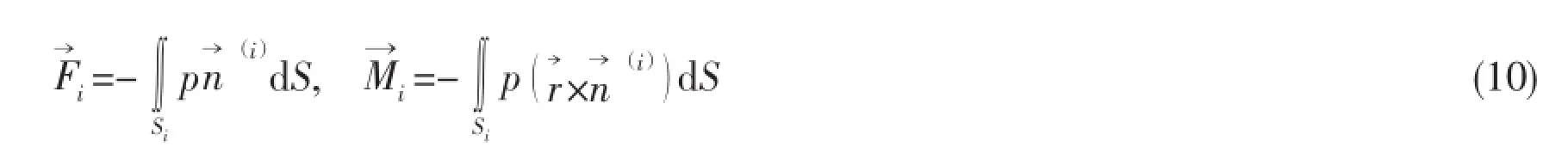
The hydrodynamic force and moment can be also represented in the standard component form.The lateral force Yi=Fi2and yaw moment Ni=Mi3on Ship i can be expressed as:

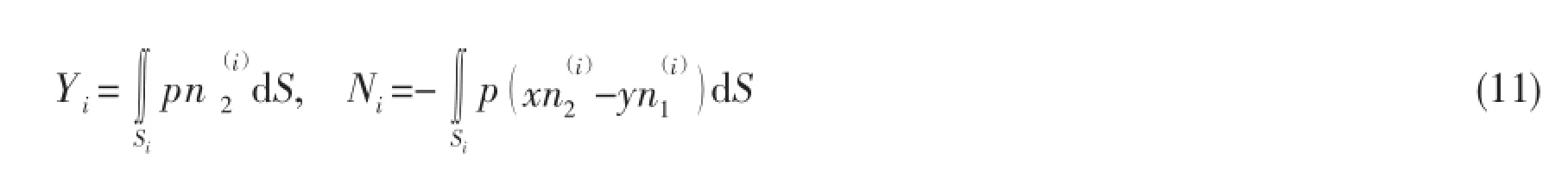
2 Solution procedure of the panel method based on NURBS

In present study,not only the body geometry,but also the source density is described by NURBS.The expressions of an arbitrary point P and the distributed source density σ on the body surface at a given moment take the forms:

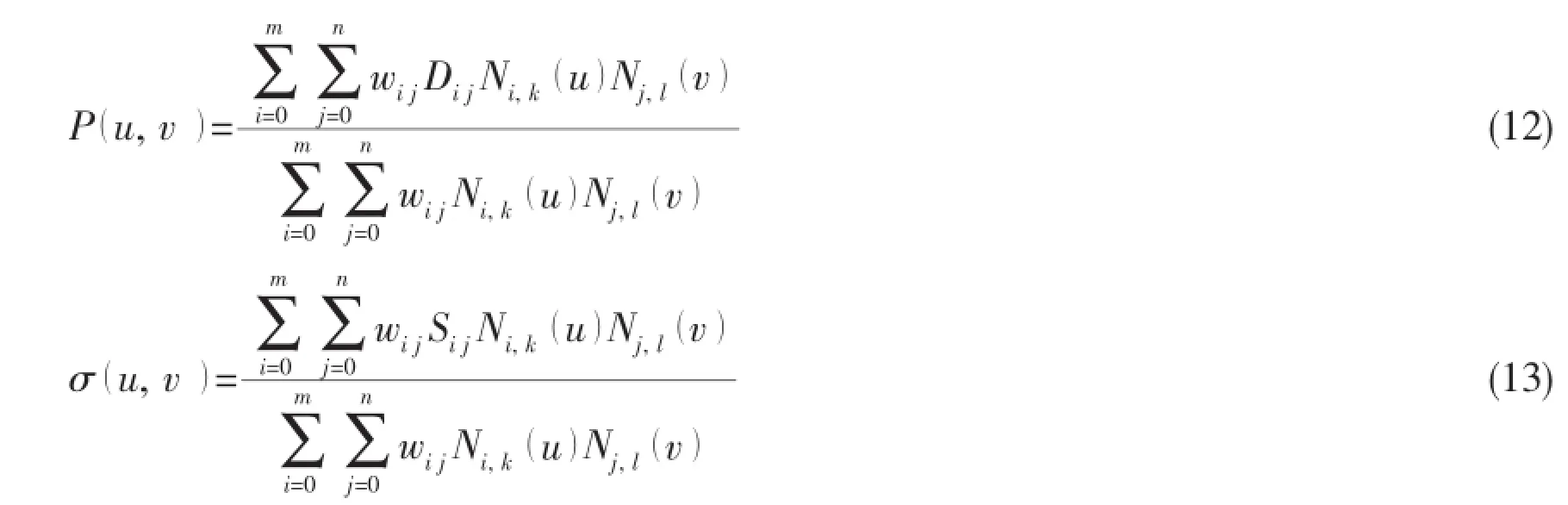
where u,v are the parameters representing two directions of the body surface and u,v∈[0,1]; Dijis the control point of the body surface,Sijis the control point of the distributed source at a given moment;wijis the weight in relation to the control points;m,n are the numbers of the control points in the u,v directions,respectively;Ni,k（u）,Nj,l（v）are the B-spline basis functions;k,l are the degrees of B-spline basis functions.In the present study,the degree of B-spline basis functions is chosen as 3,which can provide a C2-continuous representation of the body surface.

Substituting Eq.(13)into Eq.(7),it follows

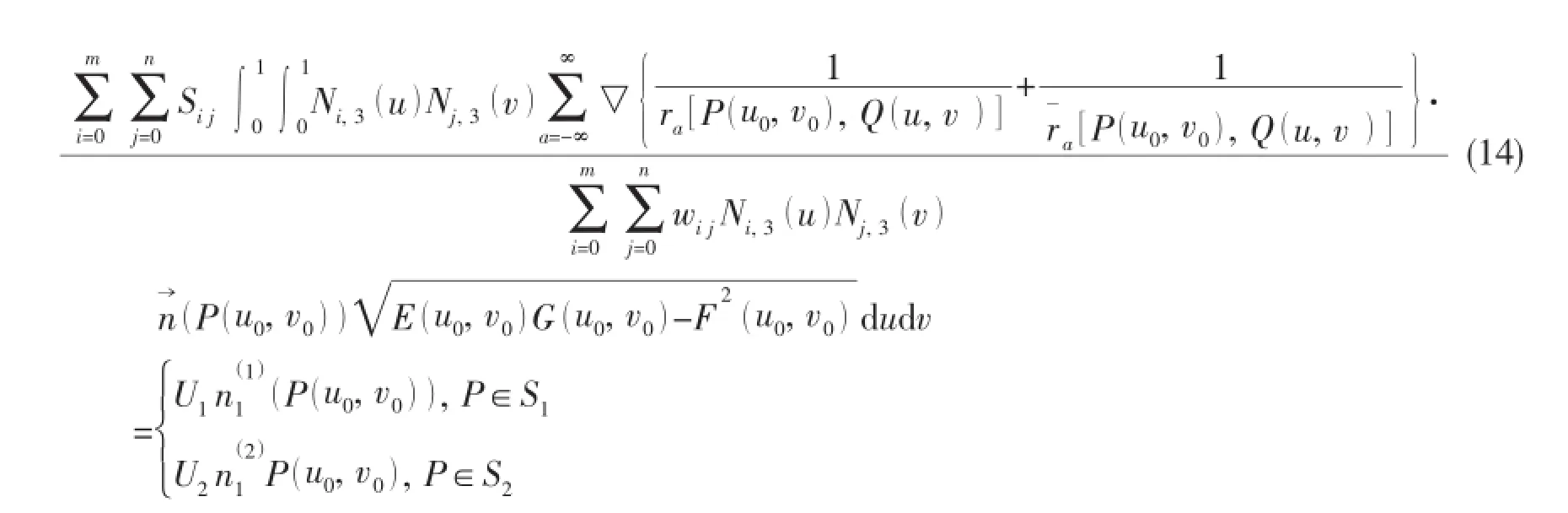
where E=Pu·Pu,F=Pu·Pv,G=Pv·Pv.

The discrete form of the second kind of Fredholm integral equation is satisfied on the collocation points P（ u0,v0）,and the source is distributed on the Gauss points of each panel on the body surfaces.

From Eq.(14),the source density control points Sijcan be obtained;then by substituting Sijinto Eq.(13),the source density on the body surfaces is obtained,and from Eq.(5),the velocity potential of arbitrary point in the fluid field can be determined.Finally,the pressure and hydrodynamic interaction forces can be calculated from Eqs.(9),(10)and(11).

3 Numerical results and discussions

Taking two Wigley hulls of same size as an example,calculations are conducted.The Wigley hull is a mathematical ship hull,whose expression is as follows:

where L,B and D are the ship length,breadth and draught,respectively.The main parameters of the Wigley hull are given in Tab.1.

ξ=2.0ST/（L1+L2）,the normalized longitudinal distance between ships,is used to replace t in the time stepping method,where Liis the length of Ship i.Considering the reality that the interaction hydrodynamic forces vanish to zero when the longitudinal distance between ships is larger than two times of ship length,the calculation starts at an initial position of ξ=-2 and ends at the position of ξ=2.In order to satisfy the assumption of low ship speed,the speeds of the ship models in the meeting case are U1=U2=0.358 9 m/s,corresponding to Fn=0.066 2;while in the overtaking case,the speeds of the ship models are U1=0.358 9 m/s and U2=0.538 4 m/s,the corresponding Froude number is Fn= 0.066 2 and 0.10,respectively.

The numerical results of hydrodynamic lateral force and yaw moment are normalized as:

Tab.1 Main parameters of the Wigley hull

According to the convergence study carried out by Xu and Zou[12]under the condition of water depth to draught ratio h/D=1.15 and the lateral distance between ships Sp=1.5B,5×16 panels on each of the ship hull and time step of 0.261 2 s are appropriate.Also,for the infinite image Green function truncated terms,a=±6 is sufficient.

3.1 Comparison of the results

The present numerical results of the hydrodynamic force and moment on Ship 1 are compared with those of the slender-body theory(Tuck and Newman[2],Yeung[3],Varyani and Krishnankutty[13]),as shown in Fig.2 and Fig.3.In these figures,the numerical results obtained by the authors using the CFD-based RANS method are also compared.

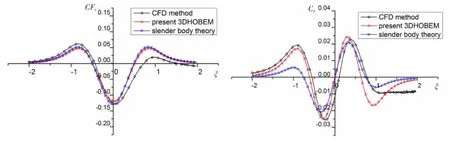
Fig.2 Comparison of lateral force and yaw moment on Ship 1 in meeting condition, h/D=1.3,Sp=1.25 m(4.17B),U1=0.358 9 m/s,U2=0.358 9 m/s

Fig.3 Comparison of lateral force and yaw moment on Ship 1 in overtaking condition, h/D=2.0,Sp=2.5 B,U1=0.358 9 m/s,U2=0.538 4 m/s

It is obvious that the interaction forces and moments emerge at the distance between two ships within 2 times of ship length and vanish to zero as the distance is becoming larger and larger both in meeting and overtaking conditions,and the interaction forces and moments are much larger in meeting case than those in overtaking case.For both conditions,the lateral forces are characterized by initial repulsion,followed by attraction and finally repulsion again; and the first repulsion peak occurs when the longitudinal distance between the bows of the two ships is zero for meeting condition or the longitudinal distance between the bow of the overtaking ship(Ship 2)and the stern of the overtaken ship(Ship 1)is zero for overtaking con-dition.The peak values of attraction occur when the two ships are abeam.Just like the first repulsion peak,the second repulsion peak occurs when the longitudinal distance between the stern of Ship 1 and the stern of Ship 2 is zero in meeting case or the longitudinal distance between the stern of the overtaking ship(Ship 2)and the bow of the overtaken ship(Ship 1)is zero in overtaking case.The change tendencies of the yaw moment are rather different from those of lateral forces.There are four phases can be distinguished for meeting condition,which are characterized by consecutive actions of bow repulsion,bow attraction,bow repulsion and bow attraction,while the yaw moment shows only two peaks,that is,consecutive bow repulsion and bow attraction for overtaking condition.In meeting case,the peak value of yaw moment occurs not only when the longitudinal distance between two ships equal to one ship length,the same position when lateral forces extremes occur,it also occurs when the distance between two ships equals to half ship length in overtaking case.

From these figures it can be seen that the present numerical method can give a qualitatively correct prediction of the change tendency of ship-ship hydrodynamic interaction forces, and the agreements between the numerical results are better in the overtaking case than in the meeting case,which means that the viscous effects do not play an important role in the overtaking case.

3.2 Influence of water depth

To investigate the influence of water depth on the hydrodynamic interaction forces,calculations are conducted for different water depth to draught ratio h/D=1.15,1.30,1.50,1.80 and 2.00,while the lateral distance between ships Sp=1.5B keeps unchanged.Fig.4 and Fig.5 show the results in meeting and overtaking conditions,respectively.

It can be seen that the change tendency is same for different water depth,and the magnitudes of the hydrodynamic interaction force and moment decrease with the increase of water depth in both meeting and overtaking conditions.The peak values of attraction lateral forces are about 2 times of the peak values of repulsion forces both in meeting and overtaking conditions at various water depths.Although all the 3 phases and change tendency of the lateral forces in both meeting and overtaking cases are the same,the peak values of correspondingly phases of overtaking case are about 13.5%smaller than those of meeting case at h/D=1.15,while with the increase of water depth,the difference is not so obvious,which means that the lateral force of meeting is more susceptible to water depth than that of overtaking.On the contrary,the yaw moment of meeting is much smaller than that of overtaking,only nearly one half.

Fig.4 Hydrodynamic force and moment coefficients of Ship 1 at different water depth during meeting,Sp=1.5B,U1=0.358 9 m/s,U2=0.358 9 m/s

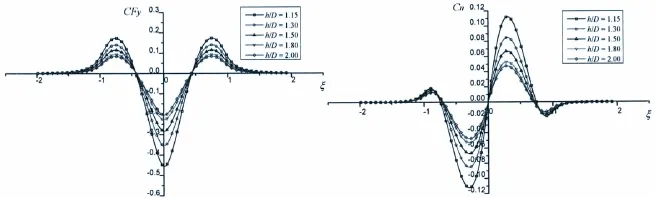
Fig.5 Hydrodynamic force and moment coefficients of Ship 1 at different water depth during overtaking,Sp=1.5B,U1=0.358 9 m/s,U2=0.538 4 m/s

3.3 Influence of lateral distance between ships

To investigate the influence of the lateral distance between ships on the hydrodynamic interaction forces,calculations are conducted for different lateral distance between ships Sp= 1.5B,2.0B,2.5B and 3.0B,where the water depth to draught ratio h/D=1.15 keeps unchanged. Fig.6 and Fig.7 show the numerical results.

Fig.6 Hydrodynamic force and moment coefficients of Ship 1 at different lateral distance between ships during meeting,h/D=1.15,U1=0.358 9 m/s,U2=0.358 9 m/s

Fig.7 Hydrodynamic force and moment coefficients of Ship 1 at different lateral distance between ships during overtaking,h/D=1.15,U1=0.358 9 m/s,U2=0.538 4 m/s

It can be seen that the change tendency is same for different lateral distance between ships,and the magnitudes of the hydrodynamic interaction force and moment decrease with theincrease of lateral distance between ships both in meeting and overtaking conditions.The similar tendency can be found,compared to the results of water depth effects.Particularly,the peak values of both lateral force and yaw moment are changing rapidly when Sp=1.5B,and the peak values of them are particularly large.It is obvious that the interaction forces are more susceptible to lateral distance in overtaking case than that in meeting case.

3.4 Influence of ship speeds during meeting

To investigate the influence of ship speeds,calculations are carried out for different ratio of ship speeds U1/U2=2.0,1.5,1.0,1/1.5 and 1/2,under h/D=1.15 and Sp=1.5B.The results are shown in Fig.8.

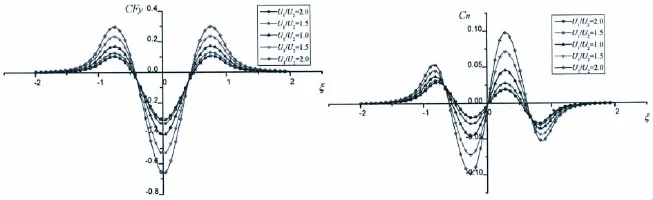
Fig.8 Hydrodynamic force and moment coefficients of Ship 1 at different ratio of ship speeds,h/D=1.15,Sp=1.5B

The change tendency of the hydrodynamic force and moment is the same as the water depth effect as described in Fig.4.The smaller the ratio of ship speeds U1/U2,the larger the force and moment on Ship 1 are.The same tendency can be found in overtaking condition.

3.5 Interaction forces on both ships during overtaking

In Fig.9,the hydrodynamic interaction force and moment acting on both ships during overtaking are compared.

Fig.9 Hydrodynamic force and moment coefficients of both ships during overtaking, h/D=1.15,Sp=1.5B,U1=0.358 9 m/s,U2=0.538 4 m/s

As it can be seen in Fig.9,the change tendency of the lateral force and yaw moment acting on both ships is same,but the peak values of lateral force and yaw moment coefficients of the slower ship(overtaken ship)are about 2 times those of the faster ship(overtaking ship) when the speed ratio U2/U1=1.5.

4 Concluding remarks

The ship-ship interaction forces both in meeting and overtaking conditions have been numerically studied by using a high-order panel method.The boundary integral equation is solved at each time step.Under the assumption of low ship speed,the effect of free surface elevation is ignored.Comparisons with slender body theory and CFD method show that the present method is effective.

The influences of finite water depth and lateral distance between ships are analyzed in detail.It is concluded that the change tendencies of the interaction forces are qualitatively same at different water depth and lateral distance between ships,but the peak values of interaction forces decrease with the increase of these parameters.Moreover,it can be found that lateral force and yaw moment are more susceptible to water depth in meeting case than those in overtaking case.On the contrary,the lateral force and yaw moment are more susceptible to lateral distance during overtaking than those during meeting.

The interaction forces and moments acting on the overtaken ship are much larger than those acting on the overtaking ship.Typically,under the condition of h/D=1.15,Sp=1.5B,and the speeds of overtaken and overtaking ships U1=0.358 9 m/s and U2=0.538 4 m/s,the interaction forces and moments acting on the overtaken ship are almost 2 times of those acting on the overtaking ship.

The present high-order panel method based on NURBS is able to predict qualitatively the tendency of the interaction forces.The further study will focus on extending the method to predict the hydrodynamic interaction between real ships with linear boundary conditions on the free surface being taken into consideration.

[1]Vantorre M,Verzhbitskaya E,Laforce E.Model test based formulations of ship-ship interaction forces[J].Ship Technology Research,2002,49:124-139.

[2]Tuck E O,Newman J N.Hydrodynamic interactions between ships[C]//10th Symposium on Naval Hydrodynamics.Cambridge,Mass.,USA,1974:35-70.

[3]Yeung R W.On the interactions of slender ships in shallow water[J].Journal of Fluid Mechanics,1978,85(Part 1):143-159.

[4]Yeung R W,Tan W T.Hydrodynamic interactions of ships with fixed obstacles[J].Journal of Ship Research,1980,24(1): 50-59.

[5]Hsiung C C,Gui Q Y.Computing interaction forces and moments on a ship in restricted waterways[J].International Shipbuilding Progress,1988,35(403):219-254.

[6]Korsmeyer F T,Lee C H,Newman J N.Computation of ship interaction forces in restricted waters[J].Journal of Ship Research,1993,37(4):298-306.

[7]Yasukawa H.Simulation of ship collision caused by hydrodynamic interaction between ships[C]//MARSIM’03,International Conference on Marine Simulation and Ship Maneuverability.Kanazawa,Japan,2003.

[8]Xiang X,Faltinsen O M.Maneuvering of two interacting ships in calm water[C].11th International Symposium on Practical Design of Ships and Other Floating Structures.Rio de Janeiro,Brazil,2010.

[9]Zhou X Q,Sutulo S,Guedes Soares C.Computation of ship hydrodynamic interaction forces in restricted waters using potential theory[J].J Marine Sci.Appl.,2012(11):265-275.

[10]Sutulo S,Guedes Soares C,Otzen J F.Validation of potential-flow estimation of interaction forces acting upon ship hulls in parallel motion[J].Journal of Ship Research,2012,56(3):129-145.

[11]Zhang X T,Teng B,Liu Z Y,et al.Computation of hydrodynamic interaction forces between ships based on B-splines[J]. Journal of Hydrodynamics,Ser.B,2003(2):83-88.

[12]Xu H F,Zou Z J.Prediction of hydrodynamic forces on a moored ship induced by a passing ship in shallow water by using a high-order panel method[J]Journal of Shanghai Jiaotong University,2016,21(2):129-135.

[13]Varyani K S,Krishnankutty P.Modification of ship hydrodynamic interaction forces and moment by underwater ship geometry[J].Ocean Engineering,2006,33(8-9):1090-1104.

基于高阶面元法的浅水域中船—船水动力相互作用数值预报

徐华福a，b，邹早建a，b，刘晓艳a

（上海交通大学a.船舶海洋与建筑工程学院；b.海洋工程国家重点实验室，上海200240）

文章开发了一种基于非均匀有理B样条（NURBS）的三维高阶面元法对浅水域中两船会遇和追越时的船-船水动力相互作用进行预报。该方法采用NURBS精确表达船体曲面，采用配置点法满足离散的边界积分方程，在边界面上的源强分布确定之后采用B样条表达物面速度势分布。基于低速假设，忽略了自由面的兴波效应，采用无穷镜像法处理刚性自由面和浅水效应，采用时间步进法在时域内求解速度势。将文中计算结果与基于RANS方程求解的CFD方法和细长体理论方法计算结果比较，验证了该方法的有效性。在此基础上，分别在不同水深、船间横向间距和船速下进行了系列的计算，分析了这些因素对船-船水动力相互作用影响。结果表明，在相同的工况下，船-船会遇时相互作用力比追越时更大，对水深变化更敏感，而对横向间距不如追越时敏感。

会遇；追越；船—船水动力相互作用；NURBS；高阶面元法

U661.1

A

徐华福（1984-），男，上海交通大学博士研究生；邹早建（1956-），男，上海交通大学教授，博士生导师；刘晓艳（1987-），女，上海交通大学博士研究生。

U661.1 < class="emphasis_bold">Document code:A

A

10.3969/j.issn.1007-7294.2016.12.004

1007-7294（2016）12-1535-12

Received date:2016-06-29

Foundation item:Supported by National Natural Science Foundation of China(51179019,51309152)

Biography：XU Hua-fu(1984-),male,Ph.D.candidate of Shanghai Jiao Tong University,E-mail:huafuxu@sjtu.edu.cn; ZOU Zao-jian(1956-),male,professor/tutor,corresponding author,E-mail:zjzou@sjtu.edu.cn.