Study on a 3D Time-domain Method to Predict Parametric Rolling of a Ship in Regular Head Seas

CHU Ji-long,WU Cheng-sheng,LU Jiang,GU Min

(National Key Laboratory of Science and Technology on Hydrodynamics, China Ship Scientific Research Center,Wuxi 214082,China)

Study on a 3D Time-domain Method to Predict Parametric Rolling of a Ship in Regular Head Seas

CHU Ji-long,WU Cheng-sheng,LU Jiang,GU Min

(National Key Laboratory of Science and Technology on Hydrodynamics, China Ship Scientific Research Center,Wuxi 214082,China)

Parametric rolling is a nonlinear phenomenon due to roll restoring variation.A three-dimensional(3D)time-domain method is used to predict parametric rolling of a ship in regular head seas.In this method,a matching surface around a ship is used to divide fluid domain into an inner domain and an outer domain.In the inner domain,the Rankine source is used to satisfy body boundary condition and linearized free surface boundary condition,while in the outer domain,the time-domain Green function is applied to meet linearized free surface boundary condition and the far field radiation condition.Froude-Krylov forces and hydrostatic restoring forces are calculated by integrating pressure under the incident wave surface.And the coupling of roll,heave and pitch,and nonlinear roll damping are considered.The numerical results are in good agreement with existing experimental results,which show that it is an efficient method for predicting parametric rolling.

parametric rolling;head seas;3D time-domain method; nonlinear restoring forces

0 Introduction

The numerical methods for direct stability assessment of parametric rolling are currently under development by the International Maritime Organization(IMO)in the second generation intact stability criteria,which will be finalized in the 4th session of Sub-Committee on Ship Design and Construction(SDC)[1].Parametric rolling as one of roll restoring variation problems is a representative nonlinear phenomenon,where a ship is excited into large roll motion even when there is no external roll excitation.

Parametric rolling always occurs in longitudinal seas with long-crested waves.When a ship is sailing through waves,due to the ship being on wave crest or trough by turns,the wetted ship surface changes in a periodic variation leading to a time-varying restoring,which is a main reason why parametric rolling occurs.So the estimation of a time-varying restoring moment is very important for a prediction method of parametric rolling.

Taguchi et al[2]predicted parametric rolling for a Post-Panamax containership in regular head seas based on a potential strip theory where Froude-Krylov forces were calculated under the instantaneous wave surface.Hashimoto et al[3]improved the calculating method of Froude-Krylov component,considering the effects of dynamic heave and pitch motions,and the radiation and diffraction,to predict parametric rolling for the PCTC in regular head seas.Numerical results overestimated roll angle in some cases.Jensen et al[4]discussed the effect of surge motion on probability of parametric rolling in irregular head seas.Umeda et al[5],Umeda and Francescutto[6]and Lu et al[7-9]executed numerical simulations of parametric rolling in regular and irregular head seas with added resistance taken into account.

The above numerical methods on parametric rolling are based on a strip method,and recently a three-dimensional(3D)panel method has been widely used in ship motion and hydrodynamic analysis,which makes it possible to consider the effect of nonlinear restoring force in a more accurate manner.

France et al[10]used an approximate‘body-nonlinear approach’(LAMP),combining the linear 3D hydrodynamics solution with the nonlinear hydrostatic restoring and Froude-Krylov forces,to study parametric rolling.LAMP based on 3D potential flow theory is used for the simulation of large amplitude motion of ships in waves.Shin et al[11]also applied LAMP to evaluate criteria for parametric roll of container ships.Their results confirmed that the codes could predict parametric rolling with sufficient accuracy.

Spyrou et al[12]used a well-known panel code SWAN2 to reproduce parametric rolling of a Post-Panamax containership.SWAN2 can solve the steady and free-surface potential flow problem around a ship using a 3D method in the time domain based on the distribution of‘Rankine’sources over the ship hull and the free surface.They concluded that the code was capable of reproducing parametric rolling growth,but it cannot consistently simulate the steady state despite the harmonic nature of the incident wave.

Kim Y[13],and Kim T and Kim Y[14-15]used WISH to analyze parametric rolling.WISH based on a time-domain Rankine panel method can be used to predict the linear and nonlinear ship motion and corresponding structural loads.

An international benchmark on the performance of computer simulation codes for the prediction of parametric rolling of ships in waves was conducted by Spanos et al[16].The 14 nonlinear time-domain numerical simulation methods,based on a strip method or a panel method, were reviewed on a comparative way with respect to the specified benchmark tests and available experimental data.The results showed that major weaknesses of the methods were related to the large amplitude wave hydrodynamics,and the methods that applied 3D hydrodynamics seemed to better reproduce the resonance conditions.

For providing a reliable prediction method for direct assessment of parametric rolling,a 3D panel method based on time-domain potential theory is used to predict parametric rolling of a ship in regular head seas in this study.

1 Mathematical formulation

1.1 The linear 3D time-domain potential theory

A problem of forward ship motion where a ship is travelling with a steady forward velocity U in an incident wave field is considered.For this problem,it is convenient to use the following three coordinate systems as shown in Fig.1.The global coordinate system OXYZ is chosen with OXY plane at the undisturbed free surface,and Z-axis being upward.The origin o of ship coordinate system oxyz is fixed on the center of gravity of the ship,x-axis points to the bow and z-axis is upward.The reference coordinate system o′x′y′z′is chosen with its origin o located on the mean free surface,z-axis pointing through the center of gravity of the ship,and coincident with the global coordinate system OXYZ at t=0.

The fluid domain is surrounded by the wetted hull surface Sb,the free surface Sfand the infinity boundary surface S∞.It is assumed that the fluid is incompressible,inviscid and its motion is irrotational.The water depth is infinite.In the fluid domain,the total velocity potentialcan be divided into as follows:

Fig.1 The coordinate systems and fluid domain

where φIis the incident wave potential,φ is the total disturbance potential including the radiation potential φRand the diffraction potential φD,t is time,andis the position vector in the global coordinate system OXYZ.φ should satisfy the following Laplace’s equation,boundary conditions and initial conditions:

where Vnis normal velocity of the body surface.In the linear 3D time-domain potential theory,the body boundary condition is satisfied under the mean free surface,and the free surface boundary condition is linearized.φ can be obtained by solving the above equations,and thenpressure p due to φTcan be computed by using Bernoulli’s equation:

Once the forces and moments acting on the hull are obtained,the displacements of the hull can be calculated by solving the ship motion equations.

For the numerical simulation of parametric rolling,the nonlinear roll restoring moment is the key to predict accurately roll motion.Here,the hydrostatic restoring forces and Froude-Krylov forces are calculated over the instantaneous wetted hull surface under the incident wave surface,while the hydrodynamic forces are still computed over the mean wetted hull surface.

The amplitude of roll angle is sensitive to the viscous effect,so the nonlinear damping should be added to the total roll moments.The nonlinear damping Mdampingcan by written as follows:

where φ is roll angle,and the coefficients N1and N3are from the roll decay tests in still water.

In head seas,the effect of dynamic heave and pitch motions for prediction of parametric rolling is significant[17].So 3-DOF motion equations of roll,heave and pitch are considered in this study.

1.2 Boundary integral equations

For solving the velocity potential in fluid domain,a mixed source method with a combination of the Rankine source and time-domain Green function is adopted.A matching surface around a ship is used to divide the fluid domain into inner domain and outer domain as shown in Fig.1.The free surface Sfis divided into two parts Sf1and Sf2by the matching surface.The inner domain is surrounded by Sb,Sf1and Sm.The outer domain is surrounded by Sm,Sf2and S∞.

1.2.1 Boundary integral equations in the inner domain

In the inner domain,Laplace’s equation,body boundary condition and linearized free surface boundary condition are satisfied.The Rankine source is distributed on all boundary surfaces,and the boundary integral equation can be written as follows:

where φIis the total disturbance velocity potential in the inner domain,G is Rankine source, G=1/r,and r is the distance of field point p and source point q on boundary surfaces.

1.2.2 Boundary integral equations in the outer domain

In the outer domain,Laplace’s equation,linearized free surface boundary condition,and far field radiation condition are satisfied.It is known that the time-domain Green function only needs to be distributed on Sm,and the boundary integral equation can be written as follows:

where φIIis the total disturbance velocity potential in the outer domain,Γmis intersection line of Smand Sf,VNis the normal velocity of Γm,and G0and Gfare associate with the time-domain Green function G,which are defined as follows:

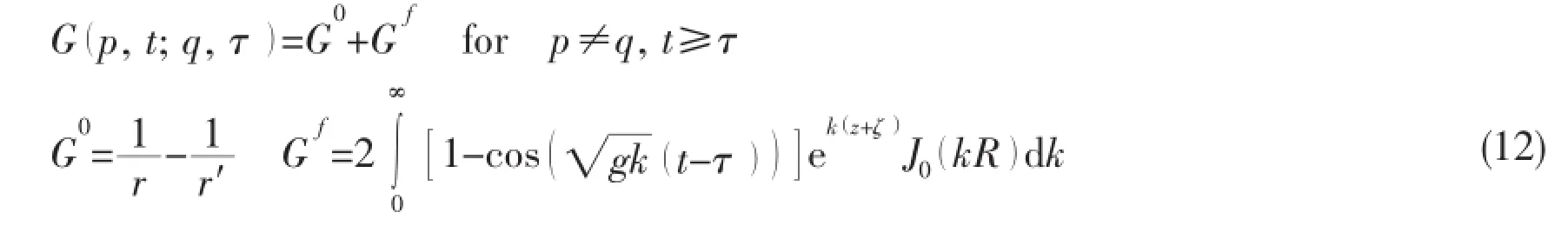
The total disturbance velocity potential and the normal velocity should be continuous on the matching surface,so there are two equations as follows:

1.3 The discretization of integral equations

The panel method is used to discretize boundary integral equations.The surfaces of Sb,Sf1and Smare separately meshing into Nb,Nf1,Nmnumbers of grids.Γmis divided into NΓsections.The boundary integral Eqs.(10)and(11)can be discretized as follows:

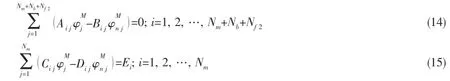
where

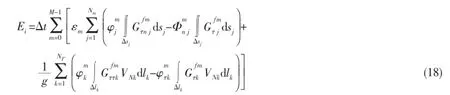
t=M△t,τ=m△τ,ε0=1/2 and εm=1(m>0),i and j are indices for p and q,respectively,and k is the index for the point on Γm.By solving the Eqs.(14)and(15),the total disturbance velocity potential on Sbcan be obtained.

2 Validations and discussions

Taking the following ship as an example,parametric rolling in regular head seas is simulated by using the above 3D time-domain method.The main particulars of the ship are shown in Tab.1.The mesh model of the hull and the fluid domain are shown in Fig.2.

Tab.1 The main particulars of the ship

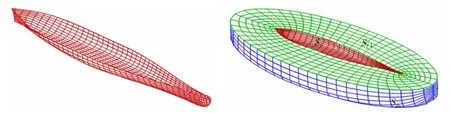
Fig.2 The mesh model of the hull and the fluid domain

The results of numerical simulation of wave,heave,pitch,roll motions in time domain are shown in Fig.3.It is clear to see that the ship occurs a large amplitude roll motion,namely parametric rolling,whose period is double wave encounter period.While the periods of heave and pitch motions are the same as wave encounter period.Meanwhile the corresponding experiment data are also shown in Fig.3 with dotted lines.It can be seen from the comparison that the roll motion in the simulation agrees well with that in the experiment,and the heave and pitch motions in the simulation are slightly larger than them in the experiment.It shows that the mathematical model can rather correctly predict parametric rolling.

But heave and pitch motions are intensively affected by parametric rolling in experiment, heave motion offsets downward,and the large and small amplitudes of heave motion appear alternately in later time,which is also observed in other experiments of parametric rolling[17-19].

The heave,pitch and roll motions are analyzed in the frequency-domain by the Fouriertransformation as shown in Fig.4.The frequency of parametric rolling mainly focuses on half of the wave encounter frequency,and the frequencies of heave and pitch motions mainly focus on the wave encounter frequency.But the frequency of heave motion in experiment also has half of the wave encounter frequency component,which is not found obviously in numerical simulation.Due to the time length of experiment data is short and parametric rolling is not developed enough,roll amplitude of experiment results in frequency domain is much lower than that in the simulation.

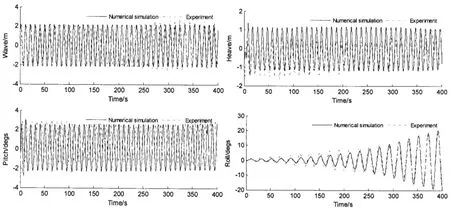
Fig.3 Development of wave,heave,pitch and roll motions in time domain (λ/Lpp=1.1,H/λ=0.02,χ=180°,U=10 Kn)

Fig.4 Heave,pitch and roll motions in frequency domain(λ/Lpp=1.1,H/λ=0.02,χ=180°,U=10 Kn)

When parametric rolling of numerical simulation develops in long time enough,the stable roll angle of the ship is up to 24 degrees as show in Fig.5.The time-varying restoring forces and the corresponding Froude-Krylov forces are shown in Figs.6-8.

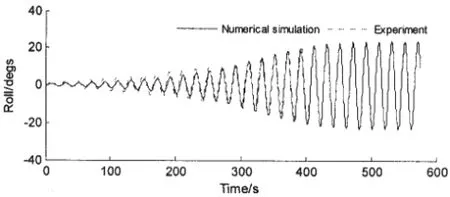
Fig.5 Development of parametric rolling in time domain(λ/Lpp=1.1,H/λ=0.02,χ=180°,U= 10 Kn)

It is found that the hydrostatic forces and Froude-Krylov forces of heave and pitch motions change with time in sine-cosine form,while roll hydrostatic moment andFroude-Krylov moment change with time in multiple frequencies form,whose periods are nearly double periods of hydrostatic forces and Froude-Krylov forces of heave and pitch motions.

Fig.6 Heave hydrostatic force and Froude-Krylov force in 3D time domain

Fig.7 Pitch hydrostatic moment and Froude-Krylov moment in 3D time domain

Fig.8 Roll hydrostatic moment and Froude-Krylov moment in 3D time domain

Using the above method,the influences of ship speeds and wave heights on parametric rolling can be obtained as shown in Fig.9,and changes of the corresponding heave and pitch motions are shown in Fig.10.

The results show that the ranges of speeds leading to parametric rolling are extended with increasing wave heights,and the amplitude of parametric rolling does not always increase with wave heights.When wave height exceeds some threshold,the amplitude of parametricrolling reduces as show in Fig.9.

Fig.9 Influence of ship speeds and wave heights on parametric rolling in regular waves (λ/Lpp=1.1,χ=180°)

3 Conclusions

As a result of a systematic study on parametric rolling in regular head seas based on a 3D time-domain potential theory,the following remarks and recommendations for the direct stability assessment on parametric rolling are noted:

(1)The 3D time-domain method in this study is feasible to predict parametric rolling for direct stability assessment.

(2)When parametric rolling occurs,the effect of roll on heave motion in regular head seas is significant in experiment,but this phenomena does not be reproduced in numerical simulations.The numerical method needs further improvement.

(3)The ranges of speeds leading to parametric rolling are extended with increasing wave heights,and the amplitude of parametric rolling may reduce,when wave height exceeds some threshold.

Acknowledgement

The study is supported by Ministry of Industry and Information Technology of China(No. [2012]533).The authors sincerely thank the above organization.

[1]IMO.Development of second generation intact stability criteria[R].SDC 2/WP.4,2015.

[2]Taguchi H,Ishida S,Sawada H,Minami M.Model experiment on parametric rolling of a Post-Panamax containership in head waves[C].Proceedings of the 9th International Conference on Stability of Ships and Ocean Vehicles,2006,1:147-156.

[3]Hashimoto H,Umeda N,Sakamoto G.Head-sea parametric rolling of a car carrier[C]//Proceedings of the 9th International Ship Stability Workshop.Germanisher Lloyd,2007:451-457.

[4]Jensen J J,Vidic-Perunovic,Pedersen P J.Influence of surge motion on the probability of parametric roll in a stationary seas state[C]//Proceedings of the 9th International Ship Stability Workshop.Germanisher Lloyd,2007:1-9.

[5]Umeda N,Hashimoto H,Stern F,Nakamura S,Sadat-Hosseini H,Matsuda A,Carrica P.Comparison study on numerical prediction techniques for parametric roll[C]//Proceedings 27th Symposium on Naval Hydrodynamics.Seoul Nat Univ,2008: 5-10.

[6]Umeda N,Francescutto A.Performance-based ship operation[C]//Proceedings 2nd International Workshop on Risk-Based Approaches in Maritime Industry.Univ Strathclyde,2008:221-229.

[7]Lu J,Umeda N,Ma K.Modeling parametric rolling in regular and irregular head seas with added resistance taken into account[C]//Proceedings of the 5th Asia-Pacific Workshop on Marine Hydrodynamics.Osaka Pref Univ,2010:93-98.

[8]Lu J,Umeda N,Ma K.Predicting parametric rolling in irregular head seas with added resistance taken into account[J]. Journal of Marine Science and Technology,2011,16:462-471.

[9]Lu J,Gu M,Umeda N.Numerical approaches on parametric rolling in head seas[C]//The 10th International Conference on Hydrodynamics.Petersburg,Russia,2012.

[10]France W N,Levadou M,Treakle T W,Paulling J R,Michel R K,Moore C.An investigation of head-sea parametric rolling and its influence on container lashing systems[J].Marine Technology,2003,40(1):1-19.

[11]Shin Y S,Belenky V L,Paulling J R,Weems K M,Lin W M.Criteria for parametric roll of large containerships in longitudinal seas[J].Trans.Soc.of Naval Architects and Marine Engineers(SNAME),2004,112:117-147.

[12]Spyrou K J,Tigkas I,Scanferla G,Pallikaropoulos N,Themelis N.Prediction potential of the parametric rolling behavior of a post-panamax containership[J].Ocean Engineering,2008,35:1235-1244.

[13]Kim Y.On Numerical Analysis of Parametric Roll:Multi-Level Approach and Uncertainty[C]//Proceedings of the Seventh International Workshop on Ship Hydrodynamics.Shanghai,China,2011:13-22.

[14]Kim T,Kim Y.Multi-level approach for parametric roll analysis[J].Inter J Nav Archit Oc Engng,2011,3:53-64.

[15]Kim T,Kim Y.Numerical study on difference-frequency-induced parametric roll occurrence[J].The International Society of Offshore and Polar Engineering,2011,21(2):111-120.

[16]Spanos D,Papanikolaou A.Benchmark study on numerical simulation methods for the prediction of parametric roll of ships in waves[C].The 10th International Conference on Stability of Ship and Ocean Vehicles,2009:627-635.

[17]Lu J,Gu M,Umeda N.Experimental and numerical study on predicting method of parametric rolling in regular head seas [C]//The 14th Internation Ship Stability Workshop.Kuala Lumpur,Malaysia,2014.

[18]Lu J,Gu M,Umeda N.A study on the effect of parametric rolling on heave and pitch motions in head seas[C]//The 13th Internation Ship Stability Workshop.Brest France,2013.

[19]Rodriguez C A,et al.Validation of a container ship model for parametric rolling[C]//Proceeding of 9th International Ship Stability Workshop.Hamburg,2007.

规则迎浪中船舶参数横摇的三维时域预报方法研究

储纪龙，吴乘胜，鲁江，顾民

（中国船舶科学研究中心水动力学重点实验室，江苏无锡214082）

参数横摇是船舶因复原特性改变而引起的典型非线性现象。文章采用三维时域方法预报规则迎浪中船舶的参数横摇运动。该方法引入匹配面将流域分为内域和外域，内域中采用Rankine源来满足物面条件和线性自由面条件，而外域中应用时域格林函数来满足线性自由面条件和远场辐射条件。数值方法中，Froude-Krylov力和恢复力是通过对船舶瞬时湿表面积积分获得，同时考虑了横摇、垂荡和纵摇三自由度之间的耦合作用，以及非线性横摇阻尼的影响。数值结果与试验结果吻合很好，说明该方法可以有效地预报参数横摇。

参数横摇；迎浪；三维时域方法；非线性恢复力

U661.32

A

储纪龙（1987-），女，中国船舶科学研究中心工程师。吴乘胜（1976-），男，中国船舶科学研究中心高级工程师。鲁江（1980-），男，中国船舶科学研究中心高级工程师。顾民（1962-），男，中国船舶科学研究中心研究员。

U661.32 < class="emphasis_bold">Document code:A

A

10.3969/j.issn.1007-7294.2016.12.002

1007-7294（2016）12-1513-10

Received date：2016-06-25

Foundation item:Supported by the Research Foundation of China(Grant No.B2420132001)

Biography：CHU Ji-long(1987-),female,engineer,E-mail:long8616767@163.com; WU Cheng-sheng(1976-),male,Ph.D.,senior engineer of CSSRC.