掺杂单晶硅纳米梁的谐振频率特性∗

吕焕玲，王静

(新疆大学物理科学与技术学院，新疆乌鲁木齐830046)

0 引言

单晶硅技术是现代集成电路技术的基础，同时纳米硅也是制造NEMS的主要材料之一．纳机电系统（NEMS）已有许多重要的应用，如超大规模传感器[1−3]、参数反馈振荡器[4]、开关[5,6]等．从长期可靠性的角度来看，这些谐振器的振动特性和机械性能，如杨氏模量和谐振频率的研究是非常重要的，应该受到研究人员的重视．对于单晶硅材料的力学特性在实验、理论分析、分子动力学模拟等方面已经做了一些研究．已有的一些实验研究了硅纳米梁、纳米线等，基于连续介质假设方程的共振特性以及共振频率与杨氏模量之间的关系[7,8]；Park等人[9,10]通过使用Tersof f势对纳米悬臂梁的振动特性进行了分子动力学模拟，并基于连续介质理论的固有频率方程推导了单晶硅纳米梁的杨氏模量，结果表明杨氏模量随硅梁厚度尺寸的减小而减小；Rudd等人[11−13]对单晶硅纳米线的弹性行为进行了基于Stillinger-Weber势的经典分子动力学模拟，随后，他们又运用了第一原理密度泛函理论计算研究了硅纳米线的力学性能，并与以前分子动力学模拟方法的结果进行了比较；2013年，Yu等人[14]通过分子动力学方法研究了不同尺寸的硅纳米梁的谐振频率和杨氏模量，结果表明硅纳米梁的谐振频率具有强烈的尺寸效应，随着厚度尺寸的增加而增加．

掺杂有利于改善硅纳米材料的力学特性．而迄今为止关于研究掺杂硅纳米材料的动态谐振特性的研究尚不多见，所以对于相关的理论研究是非常有必要的．本文采用计算机软件包Material Studio基于分子动力学方法，从守恒原理与动势能转换出发，对纳米单晶硅梁的谐振频率进行了分子动力学模拟，分别研究了掺杂浓度和尺寸对纳米单晶硅梁的谐振频率的影响．这些结果对更好地理解纳米单晶硅梁的力学性能特性是有益的．

1 分子动力学模拟纳米单晶硅谐振频率

分子动力学（Molecular Dynamics，简称MD）是模拟大量粒子集合体系中单个粒子运用的一种手法，现已成为纳米尺度上模拟的典型例子之一．1957年，Alder和wainwright[15]开创了分子动力学方法(Molecular Dynamics Simulation,简称MD)，从二十世纪八十年代开始，MD方法开始应用于半导体研究领域．本文主要运用分子动力学模拟方法，模拟改变掺杂浓度和长宽尺寸对纳米单晶硅梁的谐振频率的影响．

1.1 计算模型建立

如图1所示的一个典型的硅晶胞，可视为由四个处在不同位置的正四面体组成，正四面体的中心原子处在硅晶胞的体对角线的四分之一处，将其中任意一个正四面体平移都可以与其它的正四面体重合．

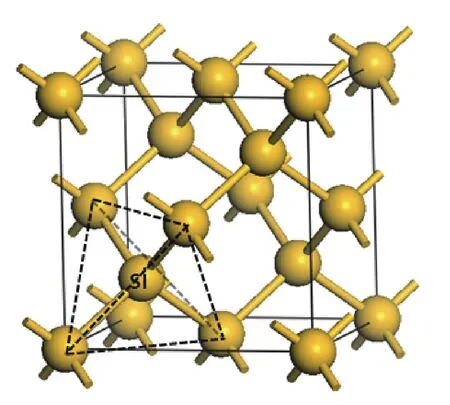
图1 硅晶胞示意图

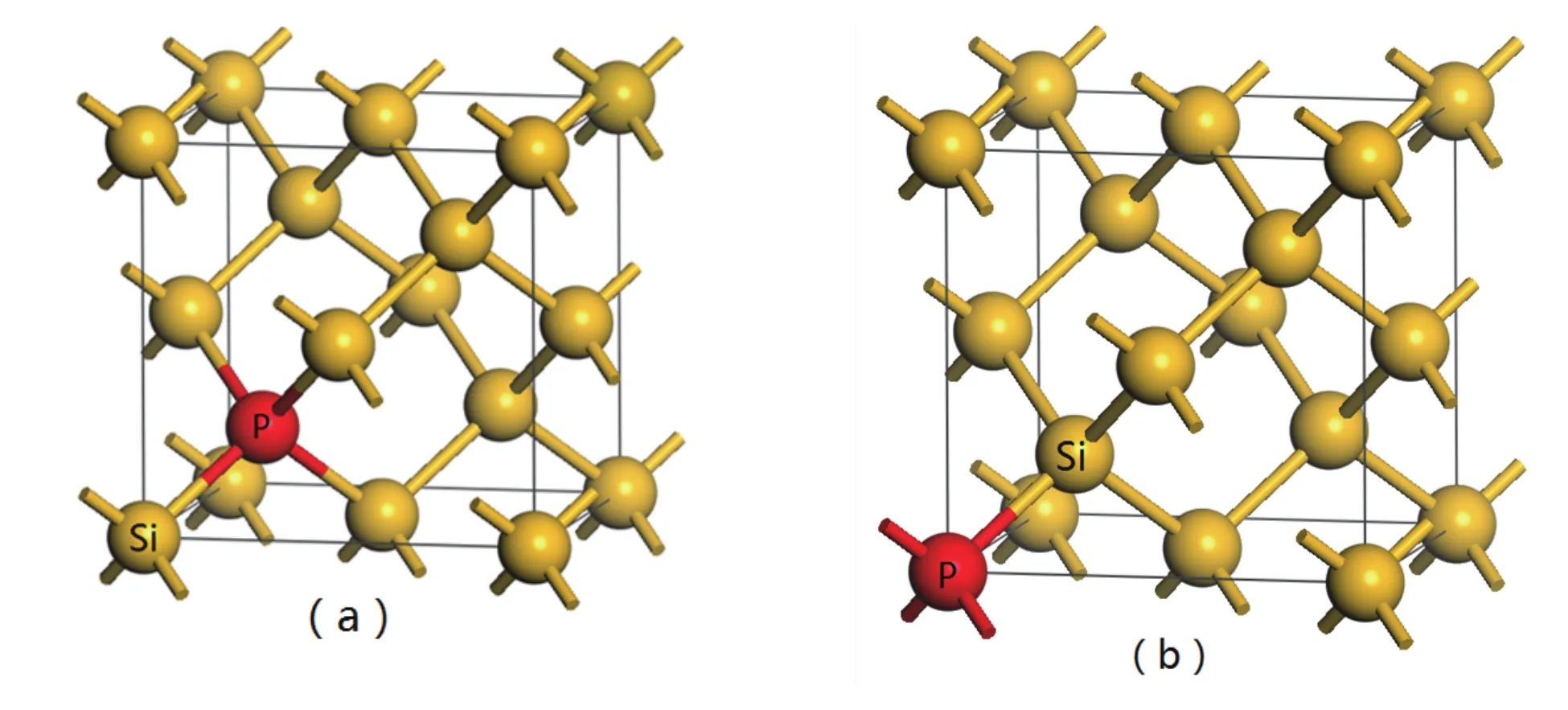
图2 (a)硅晶胞四分之一体对角线处掺杂磷元素示意图，(b)硅晶胞顶角处掺杂磷元素示意图

本文主要研究在单晶硅晶胞的两个不等价位置处掺杂一个磷原子，即四分之一对角线位置处和顶点位置，如图2（a）（b）所示．采用文献[16]数据假设，分别在2个、4个、8个、16个和32个硅晶胞中掺入磷原子，即掺杂浓度分别为30×1020cm−3、15×1020cm−3、7.5×1020cm−3、3.75×1020cm−3、3×1020cm−3．首先模拟掺杂磷的单晶硅纳米梁的横截面为一矩形，尺寸为8A×8A（A为硅晶胞的晶格常数，A=5.432˚A），梁的长度尺寸L分别为12A、16A、20A、24A、28A和32A，研究重掺杂对纳米单晶硅梁的谐振频率的影响．

1.1.1 硅晶胞四分之一对角线处掺杂

用磷原子替换硅晶胞四分之一体对角线处的硅原子，如图2（a）所示．按照不同的浓度对单晶硅纳米梁（尺寸为8A×8A×L）进行掺杂建模．建立好模型后，将所构建的晶体模型放入真空层中，防止晶体与外界进行能量交换．因此，我们需要将构建的晶体模型进行切割并加入真空层，再对纳米梁施加应变力，使梁结构产生形变，即沿宽度方向对其两端的原子进行固定，然后沿固定原子顺次向中间的每列原子下移一定距离（设下移距离为0.5˚A）并固定．最后，采用分子动力学模拟软件MS中的Forcite模块，在常温、NVE系综下进行分子动力学模拟，对纳米梁进行几何优化，模拟时间步长设为1fs，模拟时间为50ps．图3为硅晶胞四分之一对角线处掺杂，长度尺寸为32A，掺杂浓度为15×1020cm−3的纳米单晶硅梁在模拟过程中动能为零，势能最大时梁的动态振动图．

图3 单晶硅纳米梁的动态振动图

通过MS模拟得到的能量随时间的变化曲线图，如图4．通过分析图4中动势能能量的转换关系，可以得到纳米单晶硅梁的振动周期T=4.16ps，振动频率可由式f=1/T，计算得出振动频率为f=0.24×1012Hz．

同理，通过对不同的掺杂浓度和长度尺寸的纳米单晶硅梁进行分子动力学模拟，得到不同掺杂浓度和长度尺寸对应的单晶硅纳米梁的谐振频率，如表1．

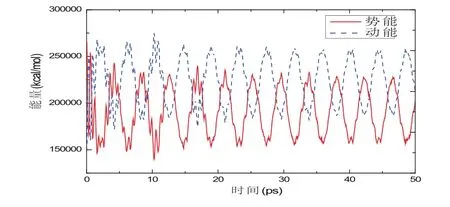
图4 长度为32A，掺杂浓度为30×1020cm−3的单晶硅纳米梁的能量随时间的变化曲线图

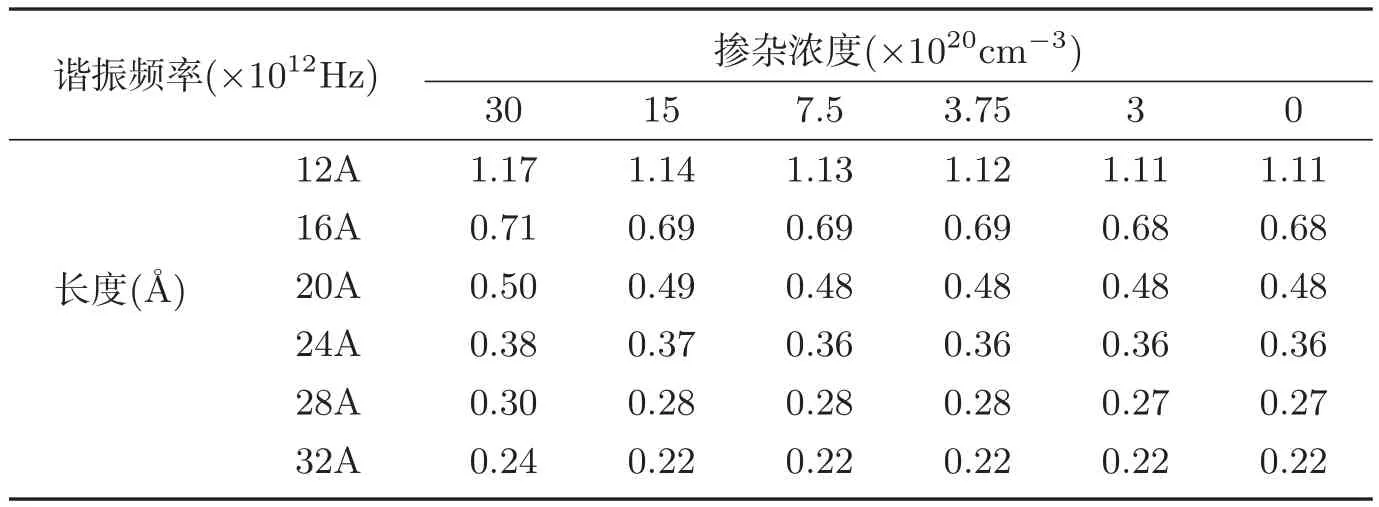
表1 不同掺杂浓度和不同长度的单晶硅纳米梁对应的谐振频率

由表1可以看出，当掺杂浓度相同时，单晶硅纳米梁谐振频率随长度尺寸的增大而减小，当长度尺寸相同时，硅梁的谐振频率随掺杂浓度的减小而减小，但减小的趋势并不明显．

1.1.2 硅晶胞顶角处掺杂

通过分子动力学方法模拟了单晶硅纳米梁在四分之一对角线处掺杂的谐振频率，同理，用磷原子替换硅晶胞顶角处的硅原子，如图2（b）所示，运用分子动力学的方法分别模拟了掺杂浓度和长度对单晶硅纳米梁谐振频率的影响，结果如表2．

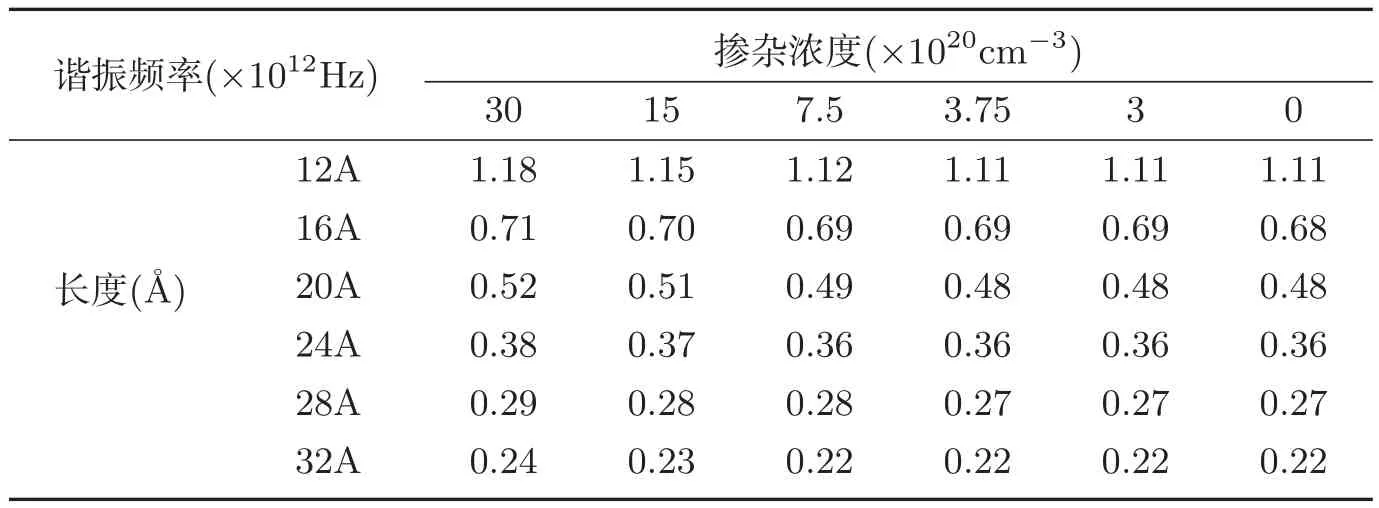
表2 不同掺杂浓度和不同长度的梁的谐振频率

由表2可以看出，当掺杂浓度相同时，单晶硅纳米梁谐振频率随长度尺寸的增大而减小，当长度尺寸相同时，单晶硅纳米梁的谐振频率随掺杂浓度的减小而减小，但减小的趋势并不明显，这个结果与表1的结果相比，变化趋势一致．

1.1.3 长度为32A的单晶硅纳米梁的谐振频率

当单晶硅纳米梁尺寸固定为32A时，选择在硅晶胞的四分之一对角线处进行磷元素掺杂，模拟掺杂浓度分别为30×1020cm−3、15×1020cm−3、7.5×1020cm−3、3.75×1020cm−3、3×1020cm−3，梁的厚度分别为2A、4A、8A、12A、16A的单晶硅纳米梁的谐振频率，结果如表3．

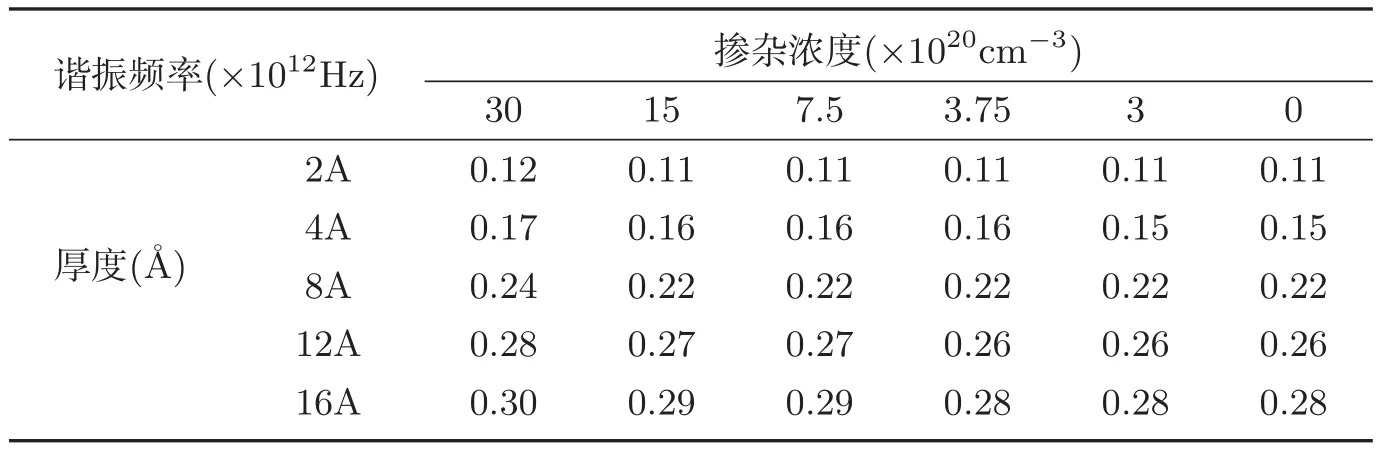
表3 单晶硅纳米梁长度为32A，不同厚度和掺杂浓度下的谐振频率

从表3可以看出，当掺杂浓度相同时，硅梁谐振频率随厚度尺寸的增大而增大；当厚度尺寸相同时，单晶硅纳米梁的谐振频率随掺杂浓度的减小而减小，但减小的趋势也并不明显．

1.2 掺杂浓度和长度尺寸对单晶硅梁谐振频率的影响

讨论掺杂浓度和长度尺寸对单晶硅纳米梁的谐振频率的影响，以在硅晶胞四分之一对角线处和顶角处掺杂的结果进行对比分析．

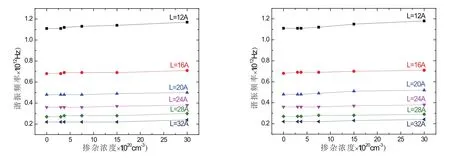
图5 不同长度尺寸和不同掺杂浓度的单晶硅纳米梁谐振频率对比图，(a)四分之一对角线处掺杂，(b)顶角处掺杂

由表1、表2得到单晶硅纳米梁的谐振频率随长度尺寸和掺杂浓度变化的曲线图，如图5（a）、（b）所示．当纳米单晶硅梁的掺杂浓度相同时，梁的谐振频率会随着长度尺寸的增加而逐渐减小，并且减小的趋势逐渐变缓，这个结果与Park等人[9]基于共振频率表达式拟合的理论曲线，谐振频率随长度尺寸的增加而减小的趋势相同．说明掺杂后的单晶硅纳米梁与纯单晶硅梁谐振频率的变化趋势一致，谐振频率具有尺寸依赖效应．当长度尺寸不变时，其谐振频率随掺杂浓度的增加而增加，但增加的趋势并不明显，且谐振频率的值十分接近，说明掺杂对纳米单晶硅梁的谐振频率影响很小．同时，通过图5（a）（b）对比可以看出，单晶硅纳米梁四分之一对角线处掺杂和顶角处掺杂的谐振频率具有相同的变化趋势，并且谐振频率值相差很小．这是因为一个单晶硅的晶胞可将其视为由四个处在不同位置的正四面体组成，正四面体的中心原子处在硅晶胞体对角线的四分之一处，将其中任意一个正四面体平移都可以与其它的正四面体重合．并且磷原子核硅原子的半径相差十分微小，当硅晶胞中一个磷原子替换硅原子，硅晶胞的结构不会发生变化，当然硅梁中掺杂更多的P原子也不会使硅梁的结构变化，并且分子动力学模拟是在真空的环境对硅梁进行优化，这时的硅梁更贴近实验中的硅梁．纳米单晶硅梁表面重构的作用相对内部原子的相互作用会对硅梁的谐振频率的影响更大，当梁尺寸越来越大表面积相对变小，内部原子变多，相互作用就会越明显，所以纳米单晶硅的谐振频率会随着尺寸的变化而变化，而掺杂浓度和位置对硅梁的谐振频率的影响并不明显．由此可知，掺杂位置不同不会影响单晶硅纳米梁的谐振频率，掺杂浓度也不是影响谐振频率的主要因素，而影响谐振频率的主要因素是单晶硅纳米梁的长度尺寸．

1.3 掺杂浓度和厚度尺寸对单晶硅梁谐振频率的影响

讨论掺杂浓度和厚度尺寸对单晶硅纳米梁的谐振频率的影响，以在硅晶胞四分之一对角线处掺杂为例，长度固定为32A的单晶硅纳米梁谐振频率随厚度变化的模拟结果进行分析．

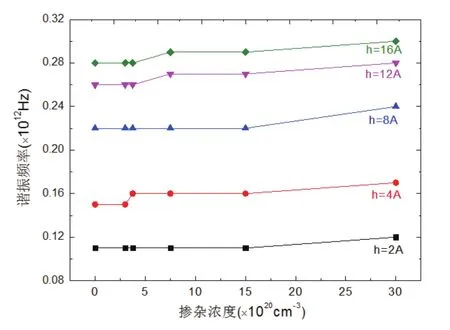
图6 不同厚度尺寸和不同掺杂浓度的单晶硅纳米梁的谐振频率对比图

由表3得到单晶硅纳米梁的谐振频率随厚度尺寸和掺杂浓度变化的曲线图，如图6．当纳米单晶硅梁的掺杂浓度相同时，硅梁的谐振频率随着厚度尺寸的增加而逐渐增加，并且增加的趋势逐渐变缓，这个结果与Yu等[14]利用分子动力学模拟方法，模拟的横截面为矩形的单晶硅纳米梁的谐振频率随厚度尺寸的增加而增大的结果一致，说明掺杂后单晶硅纳米梁的谐振频率也具有尺寸效应；当厚度尺寸不变时，其谐振频率随掺杂浓度的增加而增加，但增加的趋势并不明显，且谐振频率的值很接近，说明掺杂浓度对纳米单晶硅梁的谐振频率影响很小．由此可知，掺杂浓度不是影响谐振频率的主要因素，而影响谐振频率的主要因素是单晶硅纳米梁的厚度尺寸．

2 结论

本文主要在硅晶胞的四分之一对角线处和顶角处进行磷元素掺杂，研究纳米单晶硅梁动态的谐振特性．通过分子动力学模拟方法，研究了掺杂浓度和尺寸对单晶硅纳米梁谐振频率的影响．通过分析和讨论，得到结论如下：通过分子动力学的方法模拟了不同掺杂位置处的谐振频率，当梁的掺杂浓度和厚度尺寸一定时，单晶硅纳米梁的谐振频率随着长度尺寸的增加逐渐减小，当梁的掺杂浓度和长度尺寸固定时，单晶硅纳米梁的谐振频率随着厚度尺寸的增加而减小，当梁的长度和厚度尺寸一定时，其谐振频率随着掺杂浓度逐渐增大而增加，但是影响并不明显．由以上结论可知，掺杂浓度会影响单晶硅纳米梁的谐振频率，但是影响很小，而纳米单晶硅梁的尺寸才是影响其谐振频率的主要因素．这些结果对更好地理解纳米单晶硅梁的力学性能特性是有益的．

参考文献：

[1]Yang Y T,Callegari C,Feng X L,et al.Zeptogram-scale nanomechanical mass sensing[J].Nano Letters,2006,6(4):583-586.

[2]Yang Y T,Callegari C,Feng X L,et al.Surface adsorbate f l uctuations and noise in nanoelectromechanical systems[J].Nano Letters,2011,11(4):1753-1759.

[3]Bargatin I,Myers E B,Aldridge J S,et al.Large-scale integration of nanoelectromechanical systems for gas sensing applications[J].Nano Letters,2012,12:1269-1274.

[4]Villanueva L G,Karabalin R B,Matheny M H,et al.A nanoscale parametric feedback oscillator[J].Nano Letters,2011,11:5054-5059.

[5]Arkan E F,Sacchetto D,Yildiz I,et al.Monolithic integration of Si nanowires with metallic electrodes:NEMS resonator and switchapplications[J].Journal of Micromechanics and Microengineering,2011,21:125018.

[6]Feng X L,Matheny M H,Zorman C A,et al.Low voltage nanoelectromechanical switches based on silicon carbide nanowires[J].Nano Letters,2010,10:2891-2896.

[7]Belov M,Quitoriano N J,Sharma S,et al.Mechanical resonance of clamped silicon nanowires measured by optical interferometry[J].Journal of Applied Physics,2008,103:074304.

[8]Feng X L,He R,Yang P,et al.Very high frequency silicon nanowire electromechanical resonators[J].Nano Letters,2007,7(7):1953-1959.

[9]Park S H,Kim J S,Park J H,et al.Molecular dynamic study on size-dependent elastic properties of silicon nanocantilevers[J].Thin Solid Films,2005,492(1-2):285-289.

[10]Kim J S,Park S H,Park J H,et al.Molecular dynamics simulation of elastic properties of silicon nanocantilevers[J].Nanoscale and Microscale Thermophysical Engineering,2006,10(1):55-65.

[11]Rudd R E,Broughton J Q.Atomistic simulation of MEMS resonators through the coupling of length scales[J].Journal of Modeling and Simulation of Microsystems,1999,1(1):29-38.

[12]Rudd R E.Coarse-grained molecular dynamics for computer modeling of nanomechanical systems[J].International Journal on Multiscale Computational Engineering,2004,2:203.

[13]Rudd R E,Lee B.Mechanics of silicon nanowires:size-dependent elasticity from f i rst principles[J].Molecular Simulation,2008,34(1):1-8.

[14]Yu H,Sun C,Zhang W W,et al.Study on Size-Dependent Young’s Modulus of a Silicon Nanobeam by Molecular Dynamics Simulation[J].Journal of Nanomaterials,2013,2013:319302.

[15]Alder B J,Wainwright T E.Phase Transition for a Hand Sphere System[J].The Journal of Chemical Physics,1957,27(5):1208-1209.

[16]吕焕玲,王静.掺杂单晶硅纳米薄膜杨氏模量的多尺度理论模型[J].物理学报,2015,64(23):236103.