新疆三莎高速公路砾类土的临界动应力试验研究∗
2016-05-16刘大鹏杨晓华王婧杨晓东
刘大鹏,杨晓华,王婧,杨晓东
(1.江苏建筑职业技术学院,江苏徐州221116;2.长安大学公路学院,陕西西安710064;3.新疆交通科学研究院,新疆乌鲁木齐830000)
砾类土是新疆绿洲区常用的路基填料,随着新疆交通“三年攻坚、五年跨越”发展战略的实施,砾类土路基也会越来越多.车辆荷载施加给路基的是长期循环荷载,如果路基受到的实际动应力大于其临界动应力,路基就会破坏,因此为了保持路基的长期动力稳定性,需要明确砾类土路基的临界动应力.
对于土的临界动应力,很多学者进行了相关研究工作,刘晓红等[1]研究了原状结构红黏土的临界动应力,得到了不同条件时的临界动应力值,并考虑了含水比、围压和固结比的临界动应力经验计算公式;焦贵德等[2]研究了冻结粉土的临界动应力,分析了振动频率对临界动应力的影响规律;周葆春等[3]研究了石灰改良膨胀土在不同含水率和不同振动频率下的临界动应力,得到了含水率对石灰改良膨胀土的临界动应力影响有限,振动频率对临界动应力的影响较弱的结论;冷伍明等[4]对铁路路基粗颗粒土填料的临界动应力进行了研究,得到了不同含水率时粗颗粒土的临界动应力,并给出了临界动应力的经验计算公式;唐益群等[5]对南京地铁三山街站淤泥质粉质粘土的临界动应比进行了研究,得到了不同固结状态、不同固结比、不同轴向循环压力和频率时的临界动应比;蔡英等[6]研究了成都粘土的临界动应力,分析了加载次数、荷载频率和围压对临界动应力的影响规律.
对于砾类土的变形特性,刘大鹏等[7]曾进行了相关研究,但对其临界动应力的研究还未见报道,本文采用新疆三岔口至莎车高速公路砾类土的重塑试样进行了动三轴试验.
1 试验材料和仪器
1.1 试验材料
试验材料选用砾类土,取自新疆三岔口至莎车高速公路某路基填料场.此种类型的砾类土在新疆三岔口至莎车高速公路上应用较多,具有一定的代表性,通过筛分试验确定了砾类土的颗粒级配情况,具体如表1所示,通过室内试验确定了砾类土的基本物理力学性质,具体如表2所示.

表1 砾类土的颗粒级配

表2 砾类土的基本物理力学参数
1.2 试验仪器
动三轴试验在长安大学土工实验室进行,采用英国GDS公司生产的空心圆柱扭剪仪,该仪器可进行动、静三轴以及动、静扭剪试验,本次试验选用其中的动三轴模块、空心圆柱扭剪试验仪器如图1所示.
1.3 试验试样
由于砾类土颗粒较大,因此采用圆柱体大尺寸试样,尺寸为100×200(mm),采用空心圆柱扭剪仪配套的三瓣模制作,制作完成的试样如图2所示.

图1 空心圆柱扭剪试验仪器

图2 试样
2 试验方案
为了全面分析含水率、围压、压实度、动荷载作用频率和初始静偏应力对砾类土临界动应力的影响,进行了不同工况下的动三轴试验,采用了三种含水率,分别为7.5%(最佳含水率)、10%(大于最佳含水率)和6%(小于最佳含水率).考虑到路基和车辆荷载的实际情况[8−12],选择了3种围压,分别为10 kPa、20 kPa和30 kPa,2种压实度,分别为96%和90%,2种动荷载作用频率,分别为1 Hz和2 Hz,2种初始静偏应力,分别为0 kPa和10 kPa.动荷载采用半正弦波进行加载,具体试验方案如表3所示.
3 砾类土的εp−N关系曲线
根据试验结果绘制砾类土的εp−N关系曲线,可以发现εp−N关系曲线有三种类型,当动应力幅值σd较小,在加载初期,累计塑性εp应变随着动荷载循环次数N的增加而增加,当动荷载循环次数增加到一定程度时,累计塑性应变εp达到一定值,此后动荷载循环次数增加,累计塑性应变εp保持不变,此种类型的εp−N关系曲线为稳定型.当动应力幅值σd较大时,累计塑性应变εp会随着动荷载循环次数N增加而一直增加,当N达到一定值时,累计塑性应变εp达到破坏标准(5%),试样破坏,此种类型的εp−N关系曲线为破坏型.介于稳定型和破坏型之间的εp−N关系曲线为临界型,临界型所对应的动应力幅值σd为临界动应力.

表3 动三轴试验方案
4 不同工况下砾类土的临界动应力
4.1 含水率
当含水率为6%,动应力幅值σd为130kPa、140kPa、150kPa、160kPa、170kPa和180kPa时εp−N曲线如图3所示.含水率为7.5%,动应力幅值σd为140kPa、150kPa、160kPa、170kPa、180kPa和190kPa时εp−N曲线如图4所示.含水率为10%,动应力幅值σd为120 kPa、130 kPa、140 kPa和150 kPa时εp−N曲线如图5所示.从图3可知,当动应力幅值σd为130 kPa、140 kPa、150 kPa和160 kPa时,εp−N曲线为稳定型,动荷载循环次数N达到5 000次时,累计塑性应变εp均小于2%.当动应力幅值σd为180 kPa时,动荷载循环次数N为1 500次时,累计塑性应变εp就达到了5%,试样发生破坏,εp−N曲线为破坏型.当动应力幅值σd为170 kPa时,动荷载循环次数N为5 000次时,累计塑性应变εp约为3%,εp−N曲线为临界型,此时砾类土的临界动应力约为170 kPa.同理,从图4和图5可以得到,含水率为7.5和10%时,砾类土的临界动应力分别为180 kPa和140 kPa.可见当含水率为7.5%(最佳含水率)时,砾类土的临界动应力最大,当含水率小于最佳含水率时,临界动应力随着含水率的增加而增大,当含水率大于最佳含水率时,临界动应力随着含水率的增加而减小.
4.2 围压
围压为10 kPa,动应力幅值σd为130 kPa、140 kPa、150 kPa、160 kPa和170 kPa时εp−N曲线如图6所示,σd为130 kPa、140 kPa和150 kPa时,εp−N曲线为稳定型,σd为160 kPa时,εp−N曲线为临界型,σd为170 kPa时,εp−N曲线为破坏型,因此可得围压为10 kPa时的临界动应力为160 kPa.围压为20 kPa,动应力幅值σd为140 kPa、150 kPa、160 kPa、170 kPa、180 kPa和190 kPa时εp−N曲线如图4所示,可以得出临界动应力为180 kPa.围压为30 kPa,动应力幅值σd为160 kPa、170 kPa、180 kPa、190 kPa、200 kPa和210 kPa时εp−N曲线如图7所示,从图7可知,此时的临界动应力为200 kPa.可见围压为30 kPa时,砾类土的临界动应力最大,围压为10 kPa时,砾类土的临界动应力最小.可见围压越大,砾类土的临界动应力越大,工程中可以通过采取适当的工程措施增加路基的围压,从而来提高路基土的临界动应力.
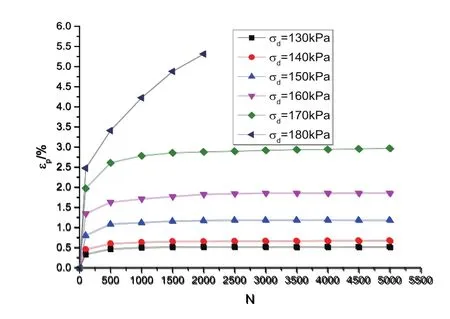
图3 含水率为6%时εp−N曲线

图4 含水率为7.5%时εp−N曲线

图5 含水率为10%时εp−N曲线
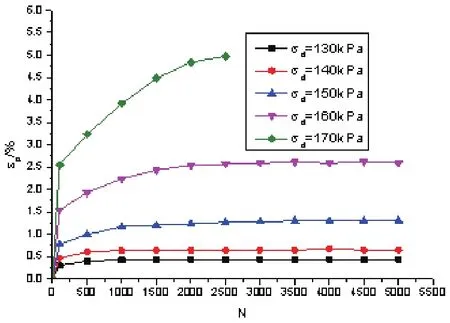
图6 围压为10 kPa时εp−N曲线
4.3 压实度
压实度为90%,动应力幅值σd为110 kPa、120 kPa、130 kPa和140 kPa时εp−N曲线如图8所示,可见动应力幅值σd为110 kPa和120 kPa,εp−N曲线为稳定型,动应力幅值σd为130 kPa,εp−N曲线为临界型,动应力幅值σd为140 kPa,εp−N曲线为破坏型,此时的临界动应力为130 kPa.其他条件相同,压实度为96%,不同动应力幅值作用下的εp−N曲线如图4所示,此时的临界动应力为180 kPa,可见随着压实度的增加,砾类土的临界动应力也增大,因此在实际工程中可以通过提高路基的压实度来增大其临界动应力.

图7 围压为30 kPa时εp−N曲线

图8 压实度为90%时εp−N曲线
4.4 动荷载作用频率
动荷载作用频率为2 Hz,动应力幅值σd为140 kPa、150 kPa、160 kPa、170 kPa、180 kPa和190 kPa时εp−N曲线如图9所示,当动应力幅值σd为140 kPa、150 kPa、160 kPa和170 kPa时,εp−N曲线为稳定型,当动应力幅值σd为180 kPa,εp−N曲线为临界型,动应力幅值σd为190 kPa,εp−N曲线为破坏型,此时的临界动应力为180 kPa.其他条件相同,动荷载作用频率为1 Hz,不同动应力幅值作用下的εp−N曲线如图4所示,此时的临界动应力为180 kPa,可见当动荷载作用频率为1 Hz和2 Hz时具有相同的临界动应力,只是在不同动应力作用下应变大小略有差别,可见动荷载作用频率对砾类土的临界动应力影响较小.
4.5 初始静偏应力
初始静偏应力为10 kPa,动应力幅值σd为140 kPa、150 kPa、160 kPa、170 kPa、180 kPa和190 kPa时εp−N曲线如图10所示,当动应力幅值σd为140 kPa、150 kPa、160 kPa和170 kPa时,εp−N曲线为稳定型,当动应力幅值σd为180 kPa,εp−N曲线为临界型,动应力幅值σd为190 kPa,εp−N曲线为破坏型,此时的临界动应力为180 kPa.其他条件相同,初始静偏应力为0 kPa,不同动应力幅值作用下的εp−N曲线如图4所示,此时的临界动应力为180 kPa,可以得到初始静偏应力为0 kPa和10 kPa时砾类土的临界动应力均为180 kPa,只是在不同动应力作用下应变大小略有差别,可见小于10 kPa的初始静偏应力对砾类土的临界动应力影响较小.

图9 作用频率为2 Hz时εp−N曲线
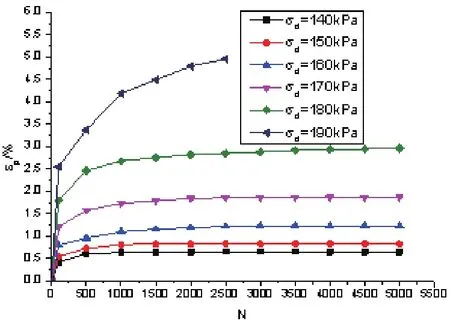
图10 初始静偏应力为10 kPa时εp−N曲线
5 结论
(1)动荷载循环作用下砾类土的εp−N曲线可分为三种类型:稳定型、临界型和破坏型;
(2)其他条件一定,当含水率为最佳含水率时,砾类土的临界动应力最大;
(3)其他条件一定时,围压越大,砾类土的临界动应力越大;压实度越大,砾类土的临界动应力越大;
(4)其他条件一定,循环荷载作用频率在1Hz∼2Hz变化时,砾类土的临界动应力变化较小.0∼10kPa范围的初始静偏应力对砾类土的临界动应力影响也较小;
(5)实际路基工程中可以通过修建路基支挡结构、在最佳含水率时压实路基土以及增大压实度等措施提高路基的长期动力稳定性.
参考文献:
[1]刘晓红,杨果林,方薇.红黏土临界动应力与高铁无碴轨道路堑基床换填厚度[J].岩土工程学报,2013,33(3):348-353.
[2]焦贵德,马巍,赵淑萍,等.高温冻结粉土的累积应变和临界动应力[J].岩石力学与工程学报,2011,30(S1):3193-3198.
[3]周葆春,白颢,孔令伟.循环荷载下石灰改良膨胀土临界动应力的探讨[J].岩土力学,2009,30(S2):163-168.
[4]冷伍明,刘文劼,周文权.振动荷载作用下重载铁路路基粗颗粒土填料临界动应力试验研究[J].振动与冲击,2015,34(16):25-30.
[5]唐益群,黄雨,叶为民,等.地铁列车荷载作用下隧道周围土体的临界动应力比和动应变分析[J].岩石力学与工程学报,2003,22(9):1566-1570.
[6]蔡英,曹新文.重复加载下路基填土的临界动应力和永久变形初探[J].西南交通大学学报,1996,31(1):15.
[7]刘大鹏,杨晓华,王婧,等.砾类土在循环荷载作用下的变形影响因素试验研究[J].铁道科学与工程学报,2014,11(4):68-72.
[8]石峰,刘建坤,房建宏,等.季节性冻土地区公路路基动应力测试[J].中国公路学报,2013,25(5):15-20.
[9]王晅,张家生,杨果岳,等.重载作用下公路路基及基层动应力测试研究[J].振动与冲击,2007,26(6):169-173.
[10]王晅.随机荷载作用下柔性路面结构及路基动力响应研究[D].长沙:中南大学,2006.
[11]凌建明,王伟,邬洪波.行车荷载作用下湿软路基残余变形的研究[J].同济大学学报(自然科学版),2002,30(11):1315-1320.
[12]赵俊明,刘松玉,石名磊,等.交通荷载作用下低路堤动力特性试验研究[J].东南大学学报(自然科学版),2007,37(5):921-925.
