果树冲击振动动态特性的研究∗

刘子龙，王春耀，魏庭鹏，吕梦露

(新疆大学机械工程学院，新疆乌鲁木齐830049)

0 前言

新疆是著名的瓜果之乡，林果业已成为新疆发展的产业支柱．随着种植规模的扩大，每到收获季节需要投入大量的劳动力，人工收获水果的速度缓慢且成本较高，若要大面积发展水果种植，必须要依靠机械化来提高采摘效率[1]．目前比较常用的机械化振动采收器械是通过振动式或冲击式激振果树，使果实脱落．振动式收获能够快速、有效地分离成熟果实，适合大面积、规模化果品生产[2]．国内外有不少学者对机械振动式果实采收机理进行了相关研究，Pacheco和Rehkugler采用撞击采摘原理，设计了一种用弹簧力撞击果树的收获机，其弹簧力的撞击速度最高可达5.16 m/s，该机适合对中型大小的苹果树进行收获[3]；Kececioglu等在利用惯性振摇器对橄榄进行收获时发现，当频率为20∼28 Hz，振幅为20∼30 mm时收获效果最好，且果实脱落效率与激振频率和振幅有关[4]；Yung和Fridley为了分析整棵树的动态特性与振动激励参数关系，将果树简化为由树干-枝条、树叶-嫩枝、果实-果柄三种不同力学特性单元组成的集合体进行研究[5]；Castro-Garcia等运用模态分析研究了果树的振动参数，固有频率和阻尼比[6]；郑甲红等对树体枝干进行三维实体建模，并进行模态分析和频率谐响应分析，得出激振频率为24 Hz时，振幅较好[7]；新疆农垦科学院机械装备研究所设计了机械振动式林果采收机试验效果良好[8]．但是只有很少一部分学者对果树能量流问题进行研究，本文力图通过试验研究，对果实实际采收过程中激振器激振频率进行研究，并对阻尼比与树枝直径的相关性进行了探讨，为下一步研究能量在果树上传递提供理论依据．

1 果树振动动力学模型及方程的建立

本文将树干、树枝视为弹性、阻尼系统，建立树干微单元振动系统，如图1所示．应用动力学定理建立振动微分方程

式中m为测点处树枝或树干等效质量、c为阻尼、k为弹簧刚度、f(t)为激励载荷．

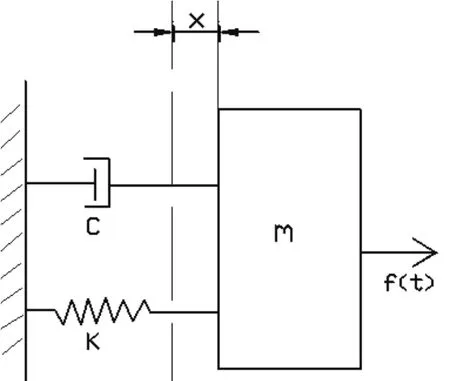
图1 微单元振动系统

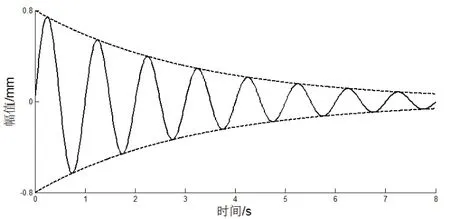
图2 有阻尼自由振动曲线

外界激振力作用在如图1所示的1点处，测点1仅在初始时受到外界干扰，测点2、3、4、5、6所受到的外界激振力f(t)=0，因此均可视为自由振动，则式（1）变为

将式（2）写为，其中,n称为衰减系数，ωn为系统无阻尼振动固有频率，定义，称为阻尼比，表示阻尼大小的一个无量纲的量[9]．所以运动方程可写为

阻尼使系统的振幅按几何级数衰减，设相邻两振幅分别为Ai,Ai−1，其比值为

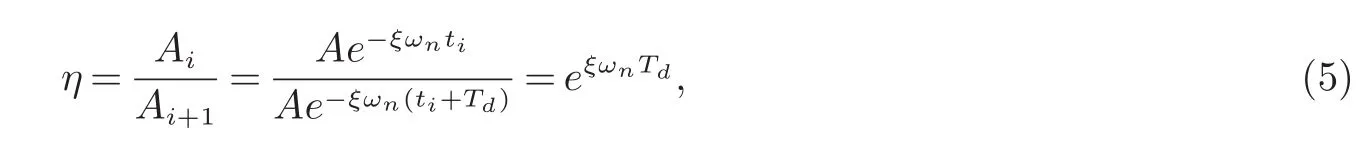
式(5)中，η称为减幅系数，n为衰减系数，n越大表示阻尼越大，振幅衰减就越快[10]．

令

δ称为对数衰减率，式（6）又可变形为

由此解得

可以通过试验测出系统振动时的振幅，为减小误差，式（7）中的i取值为2∼4[11,12]．

2 材料与方法

2.1 试验设备

试验设备为振动试验台DC-600-6、SV-0505水平滑台、功率放大器SA-5、RC-300-2振动控制仪、DH5922N动态信号测试分析系统、压电式加速度传感器DH311E、GHDAS软件等．

2.2 试验材料

试验样本为新疆地区有着5年树龄的海棠果树．

2.3 试验过程

树干底部用固定加持装置固定，在距离树干底部70 cm处安装1号加速度传感器，距离树干底部120 cm处安装2号加速度传感器，主枝上距离分叉点20 cm处安装3号加速度传感器，主枝上距离分叉点40 cm处安装4号加速度传感器，侧枝上距离分叉点20 cm处安装5号加速度，主枝上距离分叉点40 cm处安装6号加速度传感器，简化模型如图3所示，在测点1处分别施加加速度为5 g、7 g、9 g的瞬时冲击载荷．设置采样频率为500 Hz，利用DH5922N动态信号测试分析系统采集加速度信号．

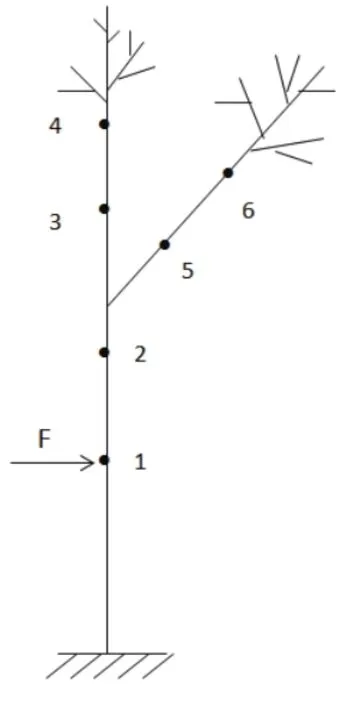
图3 各测点安装位置图

2.4 数据分析

对采集到的加速度时域信号进行快速傅里叶变换（FFT）[13,14]，得到各测点在不同激励信号作用下的加速度响应曲线，如图4中（a）、（b）、（c）、（d）、（e）、（f）所示．

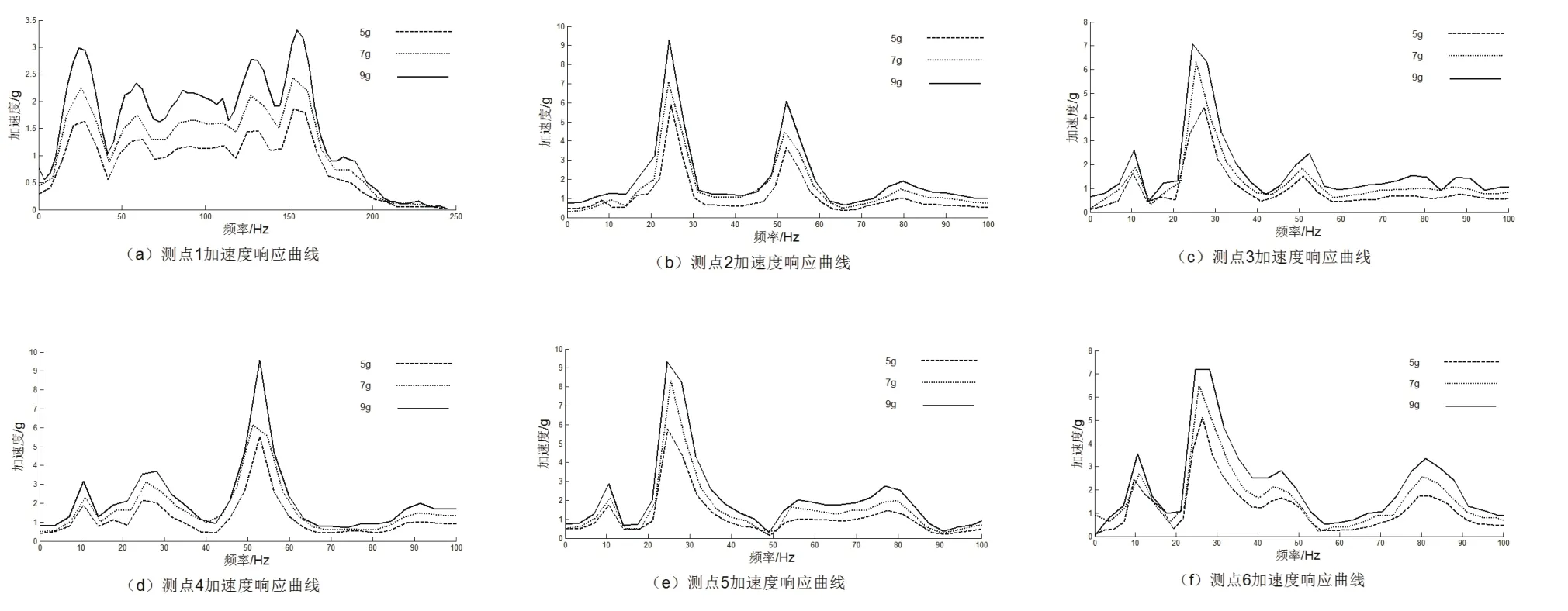
图4 各测点加速度响应

由各测点的加速度响应曲线可以看出：树干和树枝在25 Hz左右产生共振，且共振峰较大；随着外界激振载荷的增大，树干和树枝所获得的加速度值也在不断增大，其数值增加的趋势与外界所施加载荷的大小近似成倍数增加，且加速度动态响应曲线具有一定的相似性，但共振频率并未发生改变．当激振载荷作用在树干某一位置时，激振载荷的能量通过树干向两侧传递，使得果实以一定加速度运动，当果实在运动过程中产生的惯性力大于果实与果柄间的结合力时，果实脱落．在采收果实时，为提高采摘效率，使果实获得较大加速度，激振器的最佳激振频率应选择在25 Hz附近，同时在不损伤果树的情况下，激振器激振载荷尽可能选择较大值．

将采集到的加速度时域信号利用频域积分法进行积分得到位移信号，各测点位移随时间的衰减曲线如图5所示．

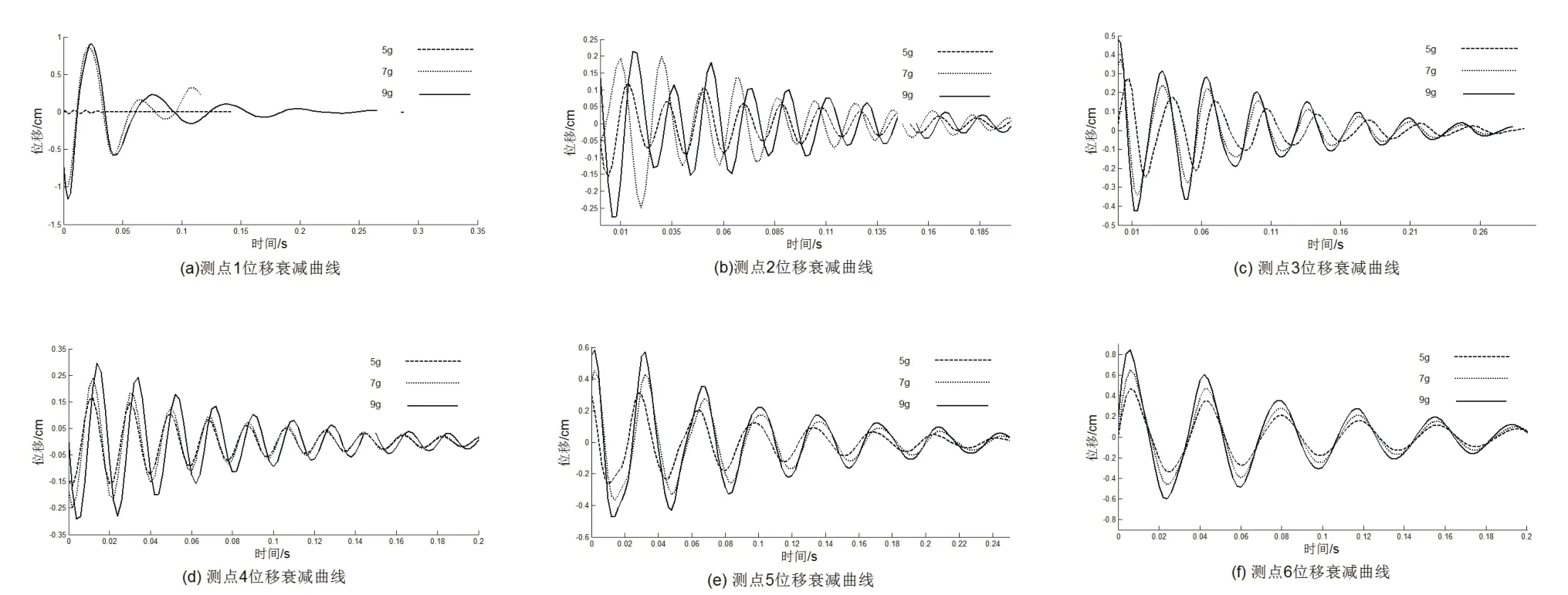
图5 各测点位移衰减曲线

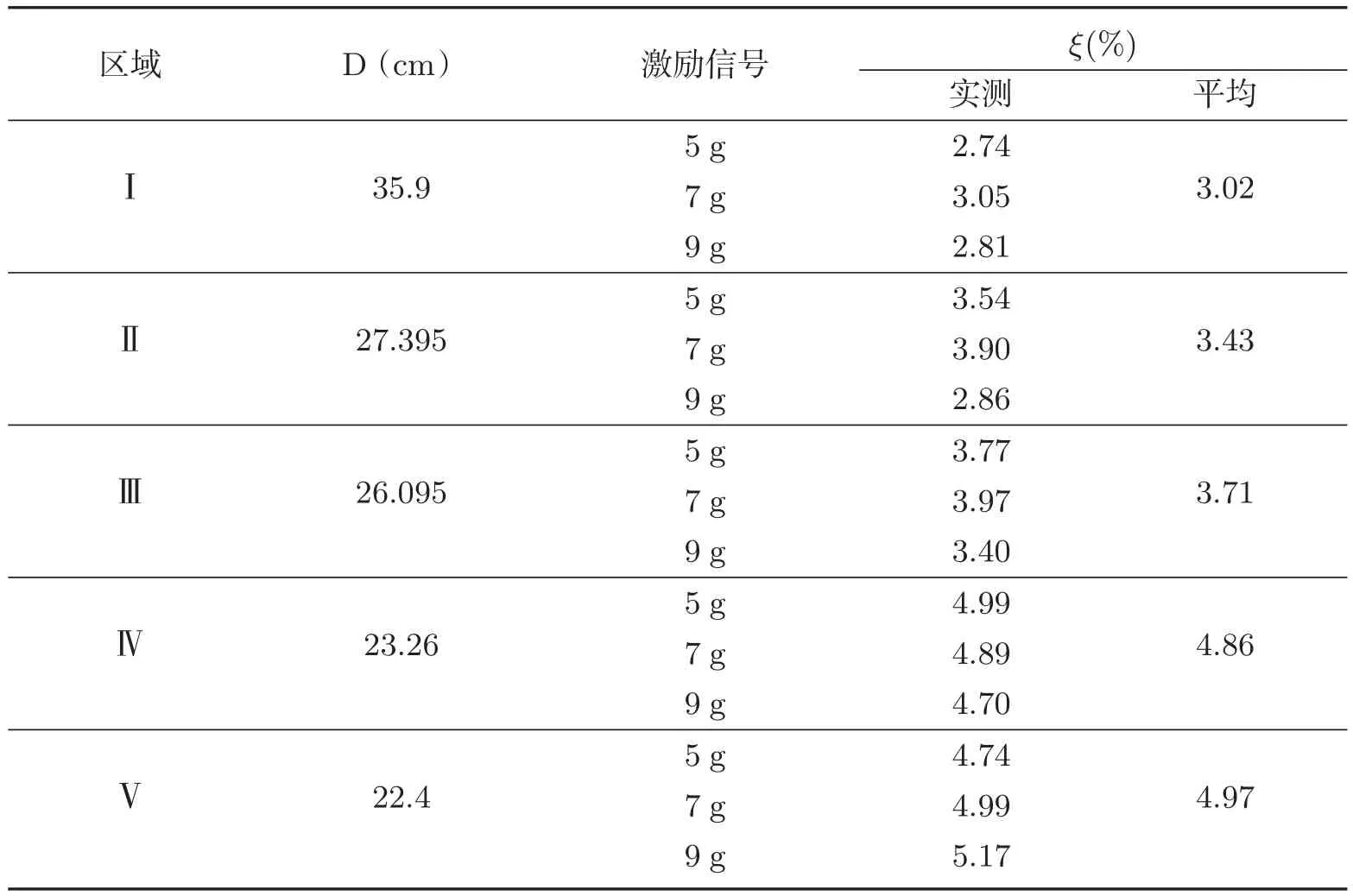
表1 不同区域枝条平均直径（D）和阻尼比（ξ）

由图5（a）可以看出，测点1直接受到载荷的作用，其位移衰减曲线特点不突出，并非自由衰减，因此，在求解阻尼比时不考虑此测点．由图5（b）、（c）、（d）、（e）、（f）可以看出，枝条被激起自由振动时，由于存在阻尼的作用，其振幅按指数规律衰减；当激振载荷增加时，各测点振幅衰减速度基本一致，振动周期基本相同；但随着激振载荷的增加，位移值也在增大；由此可以得出，枝条自由衰减振动规律与外界激振载荷无关，只与其内部属性相关．通过时域衰减的波形曲线上读取其振幅A1,A2,···Ai，利用公式（7）、（8）分别计算出各测点的对数衰减系数和阻尼比[9]．为了降低测量计算的误差，选取5 g、7 g、9 g三种激振载荷作用，并计算出三种激振载荷作用下各测点的阻尼比，再取其平均值，以减小误差，使计算结果更为准确．计算结果如表1所示，由表1可以看出，阻尼比随着树枝直径的减小而增大，且近似成线性关系．

3 结论

通过以上分析和试验可得：

（1）树干和树枝在25 Hz附近产生共振且峰值较大，所以在采集果实时，激振器给定的最佳激振力频率应选择在25 Hz附近；

（2）树干和树枝的加速度动态响应和位移曲线随着激振载荷的增大而增大，因此在不损伤果树的情况下，激振器的载荷应选择较大值；

（3）树枝阻尼比的大小与树枝的直径大小存在近似地线性关系，阻尼比随直径减小而增大；

（4）本文研究了果树树干、枝条阻尼比与直径之间的关系，可以确定在相同激励下，树枝的粗细对果实的脱落有较大影响．

本次试验研究是在室内冲击载荷作用下，将树根对果树的影响等效为刚性连接，即树干下部利用固定装置夹持，而实际上树根与土壤之间存在阻尼，属于弹性连接，下一步将对室外生长的果树进行研究，以完善相关的试验参数．本文得出了枝条阻尼比与直径的关系，为下一步研究果树能量流问题提供理论依据.

参考文献：

[1]梁勤安,楚耀辉,王晓东,等.新疆特色水果机械化收获问题的探索[J].新疆农机化,2006(4):29-31.

[2]陈度,杜小强,王书茂,等.振动式果品收获技术机理分析及研究进展[J].农业工程学报,2011,27(8):195-200.

[3]Pacheco A,Rehkugler G E.Design and development of a spring activated impact shaker for apple harvesting[J].Transactions of the American Society of Agricultural Engineers,1980,23(4):826-830.

[4]Kececioglu G.Research on olive harvesting possibilities with an inertia for tree shaker[C].Izmir:Department of Agricultural Machinery,Agriculture Faculty,Ege University,1975.

[5]Yung C,Fridley R B.Simulation of vibration of forced vibrations of tree limbs with secondary branches[J].Transactions of the ASAE,1975,18(3):475-481.

[6]Castro-Garcia S,Blanco-Roldan G L,Gil-Ribes J A,et al.Dynamic analysis of olive trees in intensive orchards under forced vibration[J].Trees-Structure and Function,2008,22(6):795-802.

[7]郑甲红,毛俊超,韩冰冰.振动式采摘机振动夹持位置的仿真研究[J].陕西科技大学学报(自然科学版),2014,32(1):142-147.

[8]汤智辉,孟祥金,沈从举,等.机械振动式林果采收机的设计与试验研究[J].农机化研究,2010,32(8):65-69.

[9]靳晓雄.汽车振动分析[M].上海:同济大学出版社,2002.

[10]刘习军.工程振动理论与测试技术[M].北京:高等教育出版社,2004.

[11]胡哲,宋显辉.振动法测量材料弹性模量与阻尼比[J].固体力学学报,2008,29(S1):155-157.

[12]王金,李玉路,邵文杰,等.基于自由振动的钢板弹簧浮置板阻尼比测试分析[J].华东交通大学学报,2015,32(5):1-5.

[13]周浩敏,王睿.测试信号处理技术[M].北京:北京航空航天大学出版社,2009:729.

[14]高飞,丁国洪,孙小刚,等.Matlab在场地微振动信号数据处理中的应用[J].勘察科学技术,2005(6):59-60+64.