浅谈课堂练习设计与思维训练

唐世强

【摘 要】数学练习是数学基础知识的应用、检测和数学知识再创造的过程。在智力结构诸能力中，思维力是智力活动的方法和核心。为发展学生的智力，我根据不同的教学环节，进行了多方位培养学生思维能力的探索。

【关键词】小学数学；课堂练习；思维训练

思维的训练与发展是数学教育最本质的内容。数学教育是关于思维的教育，数学教育的目的是启迪学生思维，培养学生思维能力，改善学生的思维品质。课堂练习作为课堂教学的重要组成部分，既要关注知识、技能的掌握，更要关注学生思维能力、情感态度与价值观的培养，为学生的可持续发展能力的培养奠定良好的基础。因此，在设计课堂练习的时候，除了设计一些基本的巩固练习外，还应设计一些开放的、能促进学生思维的练习。现结合自己的教学实践，谈谈如何设计有效的课堂练习，促进学生思维的发展。

一、一题多问，层层深入，促进学生思维深度

数学是思维的体操，数学教学最基本的目标就是使学生学会数学地思考，发展数学思维。追求数学课堂的深度思维，凸显浓浓的数学味，成为我们每一位数学教师追求的目标。然而，现在有很多的数学课堂追求的是形式上的热闹和表面上的花哨，没有深度思维，教师没有抓住数学学习的本质，没有把基本的概念和数学思维方法作为教学的重点，对教材的处理比较肤浅，很多问题的处理不到位，常给人隔靴搔痒的感觉，错失了发展学生思维的大好时机。

下面以西师版四年级下册32页《解决问题》例3教学为例，谈谈我是怎样设计课堂练习，培养学生数学思维深度的。

教学片段

师：出示练习：“小剧院共有甲票座位50个，乙票座位100个。本场电影票房收入为2300元。本场观众最少有多少人？（甲票每人30元，乙票每人10元）”。

师：哪种情况观众最少呢？

生：人数最少，就应该是票价高的50张甲票卖完。解答如下：

乙票卖的张数：（2300-30×50）÷10=80（张）

观众最少有：50+80=130（人）

师：同学们求出了观众最少有130人，那么“本场观众最多有多少人？”

生：人数最多，就应该是票价低的乙票尽量多卖。解答如下：

（2300-10×100）÷30=43（张）……10（元）

可以看出，如果乙票卖100张，甲票43张，则还差10元，所以甲票最少要卖44张，收入才会达到2300元。解答如下：

乙票张数：（2300-44×30）÷10=98（张）

最多的张数：98+44=142（张）

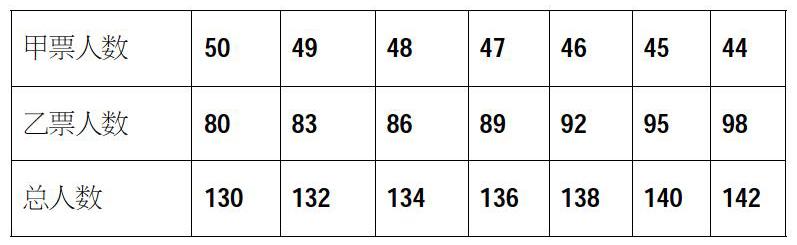
师：本场观众的人数是不是130人到142人之间都有可能？观众人数有可能是多少？

生齐答：“130至142人之间都有可能。”

师：认真思考，填写出甲、乙票人数。

学生小组合作，列表如下：

生：观众人数不是130到142人之间都有可能，只有以上7种情况。

师：认真观察表格，想一想“观众人数变化有什么规律吗？”

生：甲票人数依次减少1人，乙票人数依次增加3人，总人数依次增加2人。

师：“为什么会有这样的规律？”

生：因为甲票价钱是乙票的3倍。

改教学片段中，通过设置：“本场观众最少有多少人？”“本场观众最多有多少人？”“本场观众的人数是不是130人到142人之间都有可能？观众人数有可能是多少？”“观众人数变化有什么规律吗？”“为什么会有这样的规律？”一系列问题，引导学生由浅入深，层层深入，透彻分析。让学生明白了收入、票价固定的情况下人数的情况，了解了人数变化的规律，知道了人数变化的原因。让学生不仅知其然，而且知其所以然。这样，学生的思维的深度得到了训练，提升。

二、一题多解，促进学生思维的灵活性

（解题结果的多样性）1.设计解题策略的多样的练习

在条件和问题不变的情况下，让学生多角度、多侧面地进行分析思考，探求不同的解题途径。它可以通过纵横发散，使知识串联、综合沟通，达到举一反三、融会贯通的目的。

设计一些有不同解法和有多个答案的练习题，对于发展学生思维的灵活性和创造性有很大益处。但是，做有不同解法的练习题时，不宜让学生片面追求解法的数量，而要引导学生运用不同的思路，或运用不同的知识去解决，并且要找出简便的解法。

2.设计答案多样的开放练习

如在教学行程问题后，设计这样一道练习题：“甲、乙两个城市之间相距80千米，小东和小丽分别骑一辆自行车同时出发，小东每小时行15千米，小丽每小时行10千米，4小时后两人相距多少千米？”

学生的结论精彩纷呈，有同学考虑了两人分别从两地同向、相对、相背行驶的情况；也有同学考虑了两人从同一地点同向、相对、相背行驶的情况。针对不同情况做出了具体分析，学生从这道题的训练中，加深了对行程问题的认识，培养了学生思维的广泛性和深刻性。答案多样的练习设计要重在引导学生多思路、多层次去思考问题，鼓励学生寻求解决问题的多样化。

三、一题多变，训练学生思维的广度

教师在设计课堂练习的时候，如果能够触类旁通，对原有例题、习题进行变式，即对原题条件、问题等进行变换，就能起到举一反三和事半功倍的效果。

1.变条件

如学习了分数问题后，设计这样一道练习题。

白菜有120千克，——萝卜有多少千克？

（1）白菜是萝卜的1/3

（2）萝卜是白菜的1/3

（3）白菜比萝卜多1/3

（4）白菜比萝卜少1/3

（5）萝卜比白菜多1/3

（6）萝卜比白菜多1/3

2.变问题

如学习了平均数后，设计了这样一道练习题：“生产一批零件，第一天李师傅工作了7小时，生产了370个零件，第二天李师傅又工作了8小时，生产了390个零件，第三天王师傅工作了6小时，生产了350个零件，平均每天生产多少个零件？”

变式一、平均每小时生产多少个零件？

变式二、平均每人生产多少个零件？

对练习题进行恰当延伸、演变，从而使学生思维处于积极兴奋的状态，学生在练习过程中，克服了思维定势的消极影响，发散了学生的思维，沟通了知识间的前后练习，建构起属于自己的知识网络。

训练和发展学生思维的主要途径是的课堂练习，课堂练习的主要目的是训练和发展学生思维。简单、机械的重复练习，“题海战术”也许会提高应试教育的成绩，但过度训练会影响学生的创造能力，对促进学生思维的发展却没有任何意义。因此，精心设计课堂练习，促进学生思维发展成为迫切需要，值得我们去作出深层的思考，关系着每位老师的教育教学实践。

【参考文献】

[1]仲伟凤.《当代教育科学》，1995（3）