精心预设 促进学生对概念深刻理解

李宾

[摘 要]

数学概念教学一直是教学研讨的经典话题，特别是如何促进学生深刻理解概念。比如，圆的相关概念，多属描述性概念，关键是让学生学会辨识相关概念，如果创设问题情境，并通过恰当的追问帮助学生深刻理解与圆有关的概念。

[关键词]

圆的概念；概念教学；深刻理解

一、从“圆的概念”教学片断说起

（这是初三圆的起始课，在定义了圆之后，组织学生学习与圆相关的一些概念，如弦、弧、直径等概念）

展示一幅生活图形（如图1），并抽象、分离出图2，

教师：请同学们自学教材上与圆相关的概念，然后我们再来研究图2.

（2分钟后）

教师：现在我们把图2再标出一些字母，如图3，请同学们结合刚刚自学教材上的圆的相关概念，你能找到哪些概念呢？

学生1：我找到了圆心O，弦CD，弦AB，弦EF.

学生2：AB也是直径.

教师：为什么AB也是直径？

学生2：因为这条弦经过圆心，教材上说经过圆心的弦是直径.

学生3：这个图形中还有很多弧，比如弧CD，弧EF，等等.

教师：弧的表示方法会吗？（学生表示看书看懂了，不少学生也在下面比划着弧的样式）这里弧AB又可称为什么呢？

学生4：半圆.

教师：大于半圆的弧或小半圆的弧又称怎样的弧？

学生5：分别称优弧、劣弧.

教师：正确！让我们再回到弦的认识，图形哪条弦最大？（学生齐答弦AB）直径是所有弦中最大吗的？（学生都表示确认）进入初中以来，我们都知道几何学习十分看重推理论证，那么直径是圆中最长的弦，能否证明呢？

（学生陷入了思考，2分钟后）

学生6：如图，连接OE，OF，作OH⊥EF于H，根据等腰三角形“三线合一”可得点H为EF中点，而Rt△OEH中，OE>EH，所以2OE>2EH，即AB>EF.

教师：很好！

【课例评析】上面通过生活图片问题（圆门的图片）抽象出数学问题后，阅读教材上与圆相关的概念，然后由学生上台辨识相关概念。能过追问，精彩生成了直径是最大的弦的证明过程。

三、数学概念教学要促进学生走向深刻理解

第一，精心预设教学活动促进学生深刻理解

现代学习理论的研究表明，理解性学习的关键在于建构知识之间的联系，理解一个概念时，能否围绕这个概念逐步完善与之相关的概念网络，则对该概念就理解得越深刻。在上文中圆的概念教学片断中，我们注意到，教师精心预设了生活图片，该图片中的门框、门缝等可以抽象出图2中的弦、直径等与圆相关的概念；在追问学生直径为什么最大时，又安排学生独立思考并证明该命题，促进了学生对圆的相关概念的理解走向了较深的层次。可见，教师对待教授内容的深刻理解是第一位的，然后才可能在决定哪些概念处的教学上不惜时、不惜力。

第二，利用“圆圈”向学生揭示概念理解的层次

根据教学经验，学生数学层次的差别常常体现在学生对概念的理解的层次之上，比如上面的圆的教学片断中，层次较低的学生可能只能止步于认识弦、弧、直径这些名词，并且直观上能看得出直径是最长的弦，但是证明却不能独立贯通思路；而层次较高学生不仅能直观感知，还能严谨论证.再比如，关于《有理数》一章中相反数概念的教学，我们曾列出如下的“圆圈”（见PPT截图，图5），利用PPT渐次呈现的动画功能，揭示不同层次学生对相反数概念的理解层次。

第三，通过变式练习反馈学生对概念理解的水平

我们知道，学生数学知识的掌握往往要通过解题来表现，所以例习题的跟进教学是概念教学的重要环节，特别是围绕概念设计系列的变式问题，让学生在不同表征的习题训练之后理解、内化概念的本质，防止仅仅是形式化、表象化的理解.以后再围绕圆的起始课教学时，针对圆的相关概念设计如下的例习题，提供研讨：

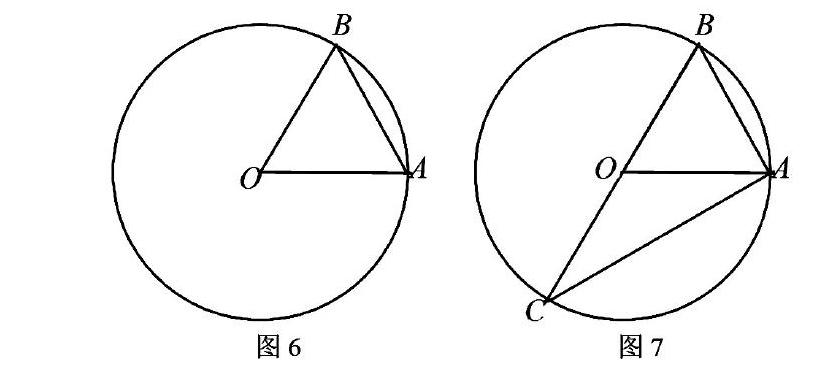
例题（原创设计）如图6，⊙O的半径OA=2 cm，点B为⊙O上一点，连接OB、AB.

（1）求OB=_______cm；

（2）当AB=2cm时，∠AOB=_____°；

（3）若∠AOB=60°时，连接AB.

①求△AOB的面积；

②作出点B关于圆心O的对称点C，连接AC，分别求AC，的长。

编题意图：圆的起始课教学时，笔者查阅了几种不同版本教材，都缺少对圆的相关概念直接训练和反馈的例习题，故笔者预设了上述习题，虽然没有直接考查默写、填空所谓的概念，但学生只要能解出（1）问，则说明他是理解了半径的概念；如果能成功解决第（2）问则说明学生发现了一个等边三角形；这为第（3）①问提供了铺垫，做好的预热工作.到最后一问，不仅训练了补全直径，同时求弦AC的长，的长也是对与圆相关概念的训练巩固。

四、写在最后

不少老师在教数学概念时，常常觉得概念是“简单内容”，学生看看定义就能理解，往往就演变为“一个概念，几项注意，讲解例题，变式再练”，很少关注概念的生成过程，没有设计一些帮助学生理解概念的问题情境，让“简单问题”教得似乎“简单化”了，缺少了数学味，也消弱了数学的育人功能.在这个角度来看，有人在最近的《数学通报》（2016年第4期）提出“让简单概念教得深刻”就是值得我们倾听的.这也是笔者创作本文的一个动机，当然我们关于概念教学的理解和一些实践还是初步的，期待批评与研讨.

[参 考 文 献]

[1]章建跃.中学数学课改的十个论题[J].中学数学教学参考，2010（3-5上）.

[2]罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，2008.

（责任编辑：张华伟）