基于Hertz接触理论的滚动直线导轨副静力学解析建模

陈　飞

(江淮汽车股份有限公司技术中心变速箱研究院，安徽 合肥 230601)



·机电工程·

基于Hertz接触理论的滚动直线导轨副静力学解析建模

陈飞

(江淮汽车股份有限公司技术中心变速箱研究院，安徽 合肥 230601)

摘要：为研究滚动直线导轨副的静力学特性，基于Hertz接触理论，从分析单个滚珠与沟槽的接触入手，在综合考虑滚动直线导轨副结构特点基础上建立静力学模型，并对其垂直方向刚度进行理论求解；然后运用CoFEM模型对该模型进行验证，进而分析不同外载荷及预紧力对滚动直线导轨副静力学特性的影响。结果表明：在不同外载荷作用下，滚动直线导轨副表现出分段非线性性质；增加预紧力可显著增加系统的刚度，从而提高系统稳定性。

关键词：直线导轨；静力学；分析模型；赫兹接触理论

滚动直线导轨副由于定位精度高、容许负载大、刚度高、变形小等突出特点，在高精度数控机床中得到了广泛的应用[1-4]。为实现高精度、高刚度、易保养等特点，滚动直线导轨副的结构比较复杂，主要由轨道、滑块、滚珠、端盖板、钢珠保持架及其他附件组成，如图1所示。滚珠在轨道与滑块沟槽之间连续滚动，使得滑块相对于轨道发生直线运动，将传统轨道与滑块之间的滑动变为滚珠与沟槽之间的滚动，大大减小了摩擦力的作用，从而减小磨损，延长使用寿命。滚动直线导轨副中，滚珠与导轨及滑块沟槽之间存在大量的接触作用。接触作用为一种典型的强非线性行为，很难获得滚动直线导轨副准确的支撑刚度。本文针对滚珠与沟槽之间的接触作用，应用Hertz接触理论对滚动直线导轨副的接触刚度进行理论求解，此思路为滚动直线导轨副的设计与选择提供借鉴。

目前，很多学者对滚动直线导轨副的静力学特性进行了研究。Dhupia 等[5]通过实验并结合Hertz接触理论，获得了滚动直线导轨副的静力学模型及其刚度; Ohta 等[6]借助有限元方法并应用Hertz接触理论，获得了滚动直线导轨副的支撑刚度。为建立准确的滚动直线导轨副静力学模型，以上2种方法分别借助实验方法及有限元方法对关键参数进行了修正。Dadalau 等[7]应用有限元理论，建立了滚动直线导轨副的CoFEM模型，并应用该模型分析滚动直线导轨副的静力学特性。文献[8-9]利用Hertz接触理论，首先建立了单个滚珠-沟槽接触模型，并将此模型应用于整体模型，通过解析方法求解滚动直线导轨副的静力学刚度。他们认为在不同载荷作用下，滚动直线导轨副的接触角不发生变化。Wu 等[10]和Hung[11]将滚珠与轨道及滑块沟槽之间的接触作用应用弹簧单元代替，获得滚动直线导轨副的接触刚度。虽然滚动直线导轨副的整体刚度很大，但是将强非线性的接触刚度应用弹簧单元来代替，不能准确反映滚动直线导轨副力学特性。

本文以典型结构的滚动直线导轨副为研究对象，应用Hertz接触理论，建立滚动直线导轨副的静力学解析模型，并应用该模型对其垂直方向刚度进行理论求解。首先，根据Hertz接触理论建立单个滚珠-沟槽接触模型；然后，将单个滚珠-沟槽接触模型引入整个滚动直线导轨副的模型中，建立整体解析模型；最后，应用CoFEM模型，验证本文所建模型的正确性。

1滚动直线导轨副接触模型

根据滚动直线导轨副的结构，建立如图2所示力学模型。图中1、2、3、4分别代表4排滚珠，为便于分析，认为滚珠均匀排列于导轨及滑块沟槽之间，每排沟槽中参与接触的滚珠数量相同(均为n)，在垂直载荷的作用下，假设同一排滚珠受力情况一致，因此，可选择导轨系统中一截面的4个滚珠及沟槽为对象进行分析。在初始预紧力的作用下，滚珠与沟槽接触发生弹性变形且变形量相同，使每排滚珠均处于被压状态，如图2所示。

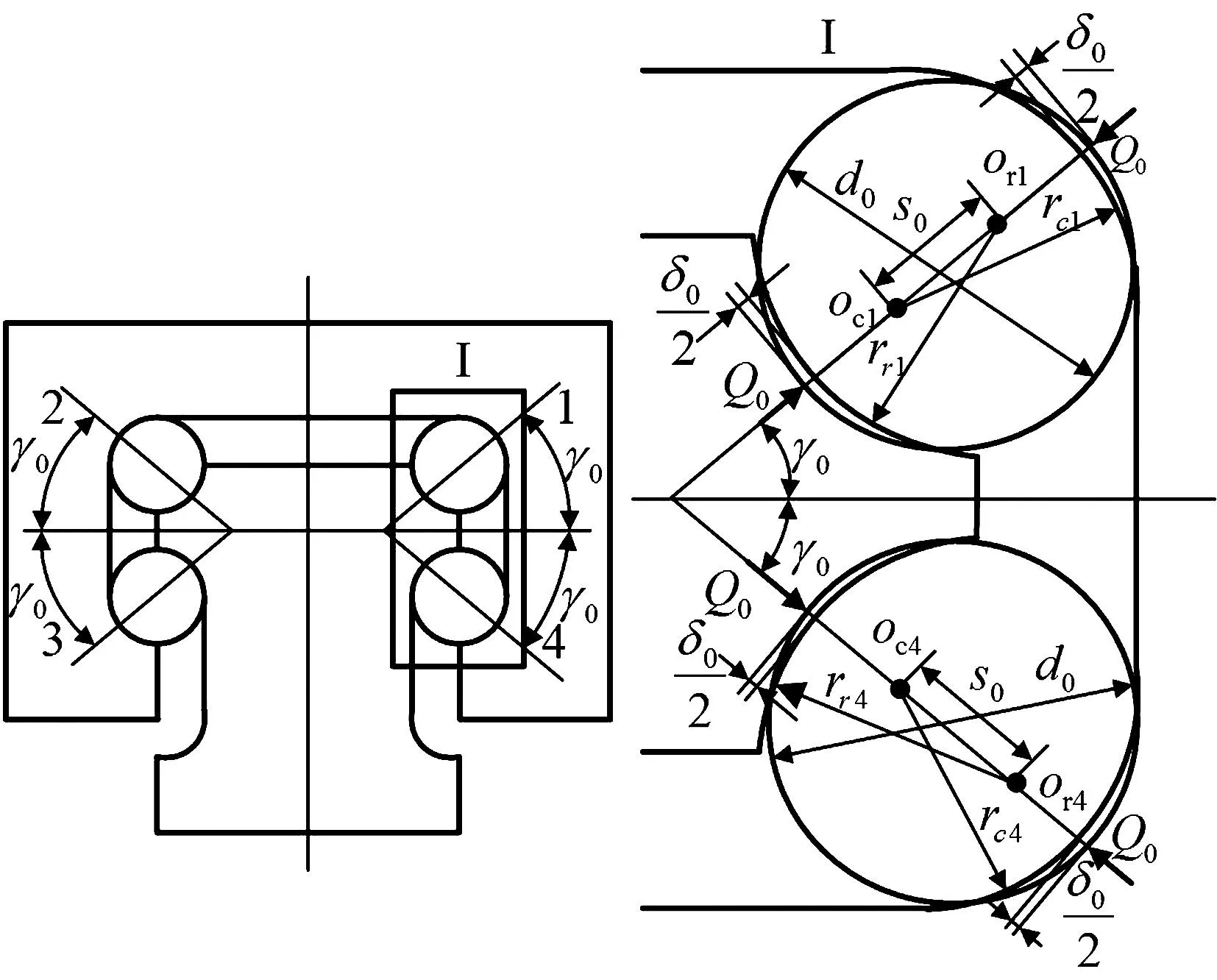
图2　滚动直线导轨副接触模型(外载荷P=0)

为获得具有高刚度特点的滚动直线导轨副，往往需要施加一定的预紧力。在预紧力的作用下，滚珠与导轨及滑块沟槽之间产生接触压力Q0，在接触压力的作用下，滚珠与导轨及滑块的接触面产生局部变形δ0,根据文献[8- 9, 12],可得

(1)

式中

其中：δc0,δr0分别为仅在预紧力作用下滚珠与滑块及轨道沟槽接触所产生的弹性变形量；E1、E2、ν1、ν2分别为滚珠、导轨及滑块材料的弹性模量(GPa)和泊松比；μ为Hertz系数；∑ρ为综合曲率(mm-1)。由于滑块与轨道的材料参数与几何参数相同，所以其变形量相等，即δc0=δr0。

根据几何关系，可以得到每排轨道沟槽曲率中心与滑块沟槽曲率中心的中心距s0，为

s0=2r-d0+δ0=m0+δ0。

(2)

由于rr、rc及d0对于具体的导轨系统而言均是常量，为计算方便，引入导轨系统几何参数m0。

图3　外载荷作用下，滚动直线导轨副接触模型(P>0)

图4　沟槽中心位置(P>0)

当滚动直线导轨副受到垂直载荷作用(P>0)时，假设导轨不发生运动，滑块将产生竖直向下的位移v，由于滑块被视为刚体，滑块各排沟槽的曲率中心的位移为v，每排单个滚珠的受力Qi(i=1,2,3,4)发生变化，每排滚珠的接触角γi(i=1,2,3,4)发生相应的变化，从而每排导轨及滑块沟槽中心距si(i=1,2,3,4)发生变化，如图3、图4所示。根据图4可以得出以下几何关系：

(3)

根据式(3)，可以得到1、4排导轨及滑块沟槽中心距s1、s4及接触角γ1、γ4：

(4)

根据中心距与滚珠弹性变形的关系，可得：

(5)

根据滚珠与沟槽接触模型，可得：

(6)

由于同一排沟槽中的滚珠的受力情况是一致的，则根据牛顿力学原理，可得

(7)

根据滚动直线导轨副的对称性，可知Q1=Q2,γ1=γ2；Q3=Q4,γ3=γ4。式(7)可化简为

(8)

根据式(3)—(8)可以得到垂直载荷P与滑块变形v之间的关系式，为

(9)

由式(9)可以看出，在垂直外载荷作用下，有预紧的直线滚动导轨系统的垂直变形v与垂直载荷P的关系不是线性关系。

随着垂直载荷P的增大，滑块各沟槽的曲率中心向下运动，上排滚珠的变形量δ1、δ2逐渐变大，局部载荷Q1、Q2增大，而下排滚珠的变形量δ3、δ4逐渐减小，局部载荷Q3、Q4减小；当δ3=δ4=0(或Q3=Q4=0)时，导轨系统达到临界状态；随着垂直载荷P的继续增大，下排滚珠失去作用，由上排滚珠实现导轨系统的支撑作用。

将δ4=0代入式(4)和式(5)可以得到滚动直线导轨副达到临界状态的滑块的位移量

(10)

将vc代入式(9)得到导轨系统的临界载荷

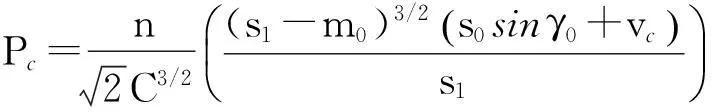
(11)

当P>Pc时，下排滚珠失去支撑作用，垂直载荷P与滑块垂直位移v的关系为

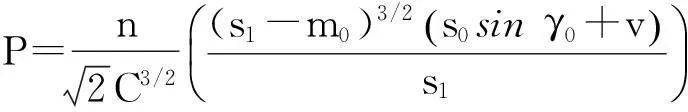
(12)

根据刚度与载荷、变形的关系，可以得到滚动直线导轨副的平均垂直刚度

KR=P/v。

(13)

2仿真验证与分析

2.1仿真验证

为验证所建模型的可行性，以文献[9]所选择的滚动直线导轨副SHS-35为研究对象进行分析，并采用文献[9]中的CoFEM模型验证本文所建模型的正确性。滚动直线导轨副的主要参数如表1所示。

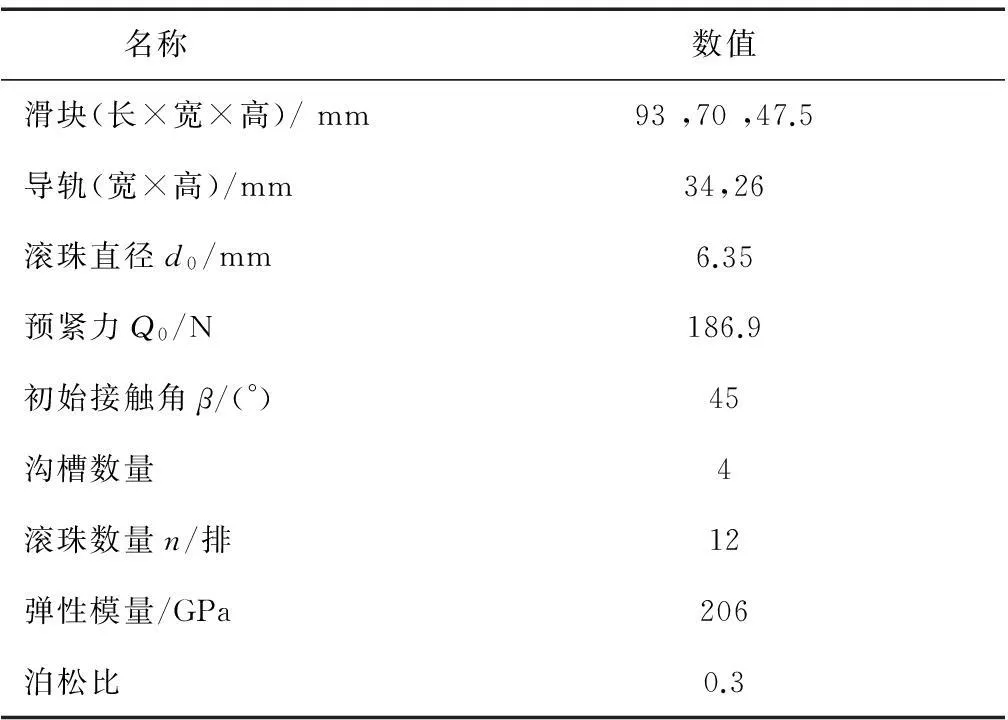
表1　滚动直线导轨副结构参数

由表1及文献[12]可得，∑ρ=0.327 mm-1,μ=0.634；因此，可计算得到参数C=0.122 μmN3/2。

图5示出采用本文所建滚动直线导轨副静力学解析模型及CoFEM模型的分析结果。在不同的载荷作用下，滚动直线副的位移不同。根据上节分析可知，由于接触非线性特性的存在，随着载荷的增加，滚动直线导轨副的位移不是线性增加的。图5(a)为本文所建解析模型与有限元模型的分析结果。可以看出：随着载荷的增加，滚动直线导轨副的位移的确不是线性增加的，与分析结果一致；解析模型与有限元模型的分析结果基本一致。这说明本文所建滚动直线导轨副的解析模型是正确的。图5(b)为不同载荷作用下，刚度与位移的关系曲线。可以看出，滚动直线导轨副的刚度曲线存在2个明显不同的阶段：在临界位移之前，随着位移的增加，刚度逐渐减小；当位移大于临界位移时，即v>vc，刚度随着位移的增加而增大。可见，滚动直线导轨副的刚度与位移关系曲线的变化趋势与上节分析结果一致。在临界位移之前，2种方法所得到的刚度存在一定的误差；但是，当位移超过临界位移以后，2种方法所得到的刚度基本一致。由此可以充分说明本文提出滚动直线导轨副的静力学模型的准确性。

(a)位移-载荷曲线

(b)位移-刚度曲线

2.2外载荷和预紧力的影响

通过上节仿真验证，说明本文所建滚动直线导轨副静力学模型的正确性。本节应用所建静力学模型分析外载荷及预紧力对滚动直线导轨副的影响。本文采用预紧力Q0分别为186.9、373.8、560.7 及747.6进行分析。图6示出不同载荷及预紧力对滚动直线导轨副静力学特性的影响。其中，图6(a)为位移-载荷曲线，图6(b)为载荷-刚度曲线。首先，分析载荷对滚动直线导轨副静力学特性的影响。可以看出，不同预紧力条件下，外载荷的影响是基本相同的。当位移小于1 μm时，滚动直线导轨副的刚度基本保持不变；当位移小于临界位移时，位移-载荷曲线随着载荷的增加，斜率逐渐减小，刚度相应的减小；当位移大于临界位移时，随着载荷的增加，位移逐渐变大，位移-载荷曲线斜率逐渐增大，刚度也随着增大。可见，随着外载荷的不同，滚动直线导轨副表现出分段非线性的性质。

接下来，分析预紧力对滚动直线导轨副静力学特性的影响。从图6(a)位移-载荷曲线可以看出，无论位移是位于临界位移之前还是之后，在相同的外载荷作用下，随着预紧力的增加，位移逐渐减小。在相同的载荷条件下，随着预紧力的增加，滚动直线导轨副的刚度逐渐增大。当载荷小于临界载荷时，随着载荷的增加，不同预紧力作用下的刚度差基本保持不变；当载荷大于临界载荷时，随着载荷的增加，不同预紧力作用下的刚度差逐渐减小。从分析结果可知，滚动直线导轨副的刚度受到外载荷及预紧力的影响。

(a)位移-载荷曲线

(b)载荷-刚度曲线

图7示出滚珠与沟槽接触局部受力情况。其中，图7(a)示出上排滚珠与沟槽接触局部接触力Q1的变化情况；图7(b)示出下排滚珠与沟槽接触局部接触力Q2的变化情况。从图7(a)可以看出，随着载荷的增加，上排滚珠局部接触力逐渐增加，且斜率逐渐增加，与分析结果一致，单个滚珠与沟槽的接触同样表现出非线性。当载荷小于临界载荷时，增大预紧力，上排滚珠的局部接触力增加；当载荷大于临界载荷时，上排滚珠的局部接触力是一样的，但是由于位移随着预紧力的增加而减小(见图6)，整体刚度增加。从图7(b)可以看出，随着载荷(位移)的增加，下排滚珠的接触力逐渐减小，当达到临界载荷(位移)时，减为0。随着载荷(位移)继续增加，下排滚珠的接触力始终为0，不发生变化。随着预紧力的增加，下排滚珠接触力变为0时的载荷(位移)增加，即临界(载荷)位移增加，与整体分析得出相同的结论。从上述分析可知，滚动直线导轨副表现出分段非线性的性质，以及增加预紧力以增加系统刚度的原因为单个滚珠与沟槽接触的非线性及接触的不可拉伸性。

(a)载荷-接触力Q1曲线

(b)载荷-接触力Q4曲线

3结论

本文基于Hertz接触理论，在充分考虑滚动直线导轨副结构特征的基础上，建立滚动直线导轨副的静力学解析模型，并应用该模型对其垂直方向刚度进行理论求解，采用CoFEM方法对所建模型进行了验证，从而证明了本文所建滚动直线导轨副静力学模型的正确性。最后，应用该模型分析了外载荷及预紧力对滚动直线导轨副静力学特性的影响。研究结果表明： 1)在不同的外载荷条件下，滚动直线导轨副表现出分段非线性的性质; 2)增加预紧力可以显著增加滚动直线导轨副的刚度，从而提高系统的稳定性； 3)单个滚珠与沟槽的接触非线性和接触本身的不可拉伸性决定了滚动直线导轨副的分段非线性的性质，为增加预紧力可提高系统刚度提供了理论参考。

参考文献

[1]Yin Z, Marc B, Tao H. Design of a Linear Guideway on Rolling Elements for Ultra Precision Meso-machine Tools[C]//2010 International Conference on Mechanic Automation and Control Engineering. Wuhan: IEEE, 2010:3053-3056.

[2]Ohta H. Sound of Linear Guideway Type Recirculating Linear Ball Bearings[J].Journal of Tribology, 1999,121:678.

[3]Ohta H, Hayashi E. Vibration of Linear Guideway Type Recirculating Linear Ball Bearings[J].Journal of Sound and Vibration, 2000，235：847.

[4]Ohta H, Nakagawa T. Using Ceramic Balls to Reduce Noise in a Linear Guideway Type Recirculating Linear Ball Bearing [J].Journal of Tribology, 2003,125(3):480.

[5]Dhupia J S, Ulsoy A G, Katz R, et al.Experimental Identification of the Nonlinear Parameters of an Industrial Translational Guide for Machine Performance Evaluation [J].Journal of Vibration and Control, 2008 (14)： 645.

[6]Ohta H, Tanaka K.Vertical Stiffnesses of Preloaded Linear Guideway Type Ball Bearings Incorporating the Flexibility of the Carriage and Rail [J].Journal of Tribology-Transactions of the Asme, 2010，132(1)：1.

[7]Dadalau A, Groh K, Reuß M, et al. Modeling Linear Guide Systems with CoFEM: Equivalent Models for Rolling Contact [J]. Production Engineering, 2012(6):39.

[8]孙伟, 孔祥希, 汪博, 等. 直线滚动导轨的Hertz 接触建模及接触刚度的理论求解[J].工程力学, 2013, 30(7): 230.

[9]Sun W, Kong X, Wang B, et al. Statics Modeling and Analysis of Linear Rolling Guideway Considering Rolling Balls Contact[J].Proceedings of the Institution of Mechanical Engineers Part C:Journal of Mechanical Engineering Science, 2015, 229 :168.

[10]Wu S S,Chang J C, Hung J P. The Effect of Contact Interface on Dynamic Characteristics of Composite Structures[J].Mathematics and Computers in Simulation, 2007,74(6):454.

[11]Hung J P. Load Effect on the Vibration Characteristics of a Stage with Rolling Guides [J].Journal of Mechanical Science and Technology, 2009,23(1):89.

[12]戴曙.机床滚动轴承应用手册[M].北京：机械工业出版社， 1993： 13-35.

(编校：饶莉)

Static Analytical Modeling of Linear Guide Based on Hertz Contact Theory

CHEN Fei

(JianghuaiAutomobileCompanyTechnicalCenterTransmissionR&DAcademy，Hefei230601China)

Abstract:To study the static characteristic of the linear guide , the ball-groove contact model is developed based on the Hertz contact theorem. By using the ball-groove contact model, the analytical static mode of the linear guide is established. Moreover, the CoFEM model is utilized to verify the feasibility of the proposed analytical model . Finally, the effects of load and preload on the static model are discussed based on the analytical model. The results indicate that the linear guide has piecewise-nonlinear characteristic in different loads. Additionally, the stiffness of the linear guide can be increased significantly by increasing the preload on the system as well as the stability.

Keywords:linear guide; static; analytical modeling; Hertz contact theory

doi:10.3969/j.issn.1673-159X.2016.02.008

中图分类号：TH132

文献标志码：A

文章编号：1673-159X(2016)02-0039-5

作者简介：陈飞(1988—)，男，硕士，工程师，主要研究方向为机械传动系统。E-mail：13721051629@163.com

收稿日期：2015-10-29