设计参数不确定条件下滚动直线导轨运动性能分析

2024-04-12李云峰

组合机床与自动化加工技术 2024年3期

李云峰

(三江学院机械与电气工程学院,南京 210012)

0 引言

滚动直线导轨具有定位精度高、摩擦系数小、精度保持性好、可维护性好等优点,因此在主轴系统和进给系统中广泛应用,已经成为了数控机床重要的功能部件[1-2]。直线导轨的运动特性直接影响到产品的加工精度和质量,因此研究滚动直线导轨的动态运动性能具有重要的意义[3-4]。

影响滚动直线导轨动态运动性能的因素很多,一般从摩擦、磨损、预紧力和装配误差等方面开展研究工作。YI等[5]通过研究摩擦对导轨微观和宏观的动态特性的影响规律,对直线导轨位置精度进行了研究工作。ZOU等[6]研究了直线导轨在使用过程中由于摩擦和磨损的影响而引起的接触刚度变化,建立导轨接触刚度预测模型。TAO等[7]建立了滑块滚道磨损引起的位移计算模型,对直线导轨的磨损和性能进行预测。梁医等[8]分析了滚道中心距不同误差情况下对滚动直线导轨承载能力的影响规律。KONG等[9]综合考虑预紧力、初始接触角和球径等因素的影响,研究了线性导轨的动态特性和稳定性。

但是,在实际工程中,由于不能完全消除参数的随机性,不可避免地存在如材料性能、几何尺寸、载荷等着不确定因素,导致了直线导轨运动特性的不确定性[10]。针对此问题,WANG等[11]利用正太分布表征几何参数的不确定性,采用随机摄动法计算动态误差的统计矩,实现对直线导轨动态运动性能的分析。然而,由于工程问题的复杂性和样本数量的限制,很难得到参数精确的概率分布[12]。假设几何参数服从特定的概率分布,即使是偏离真实值的微小变化,也可能造成较大的计算误差[13]。虽然无法准确定义不确定参数的概率分布,但是可以比较容易确定参数的上下界,因此可以用区间模型来处理参数的不确定性[14]。区间分析方法仅需知道不确定参数的上下界,可以更大程度保留参数的原始信息,使得分析计算结果更符合实际情况,因此得到了广泛的应用[15-16]。

目前,尚未有关于设计参数不确定性对滚动直线导轨运动性能的研究。本文利用区间模型表征直线导轨设计参数的不确定性,通过分析直线导轨实际受载情况并基于Hertz接触理论,建立了滚动直线导轨二自由度动力学分析模型;然后,利用龙格-库塔法进行求解,得到各个时刻直线导轨的动态响应值。以SHS-45R系列滚动直线导轨为例,利用本文所述方法对不同精度等级的导轨运动性能进行了分析。

1 直线导轨动力学分析模型

1.1 直线导轨受力模型

直线导轨在实际运行过程中,受到复杂的工作载荷的作用,考虑到实际工作情况,假设直线导轨受到垂直载荷Fy和水平载荷Fx的作用,如图1所示,并假设Fx和Fy均为简谐激振力[17]。

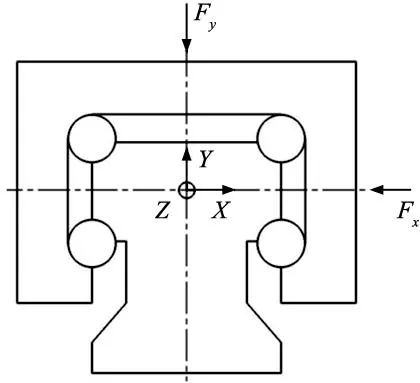
图1 直线导轨受力分析图

1.2 直线导轨定位误差分析

直线导轨精度公差包括行走平行度公差与尺寸公差[11]。如图2所示,导轨的几何公差包括M向的公差ΔA以及W向的公差ΔB,通过提高安装精度可以降低几何误差[18]。直线导轨实际工作过程中,由于载荷的作用,产生垂直位移V和水平位移H。由于几何参数的不确定性,导致滑块各个时刻V和H的值出现波动,由此造成导轨运动过程中的平行度误差。

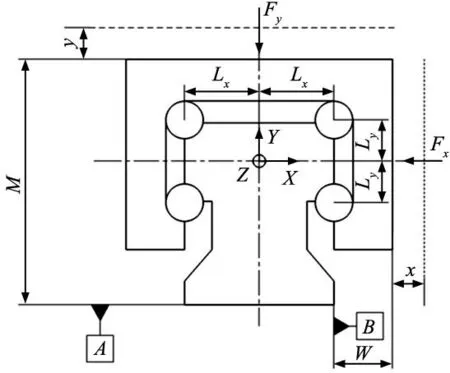
图2 滚动直线导轨的精度公差

1.3 接触变形与载荷分析

图3为直线导轨的结构组成,主要包括滑块、滚珠和导轨3部分。导轨受到载荷Fy、Fx的作用,因此滑块产生垂直位移V、水平位移H。4列滚珠编号为i(i=1,2,3,4),第i列滚珠受到的接触面法向载荷为Qi(i=1,2,3,4)。根据Hertz理论,对滚珠与滚道的接触进行分析,滚珠与轨道与滑块接触模型如图4所示。Oci和Ori为滑块和导轨沟槽初始曲率中心,曲率半径分别为Rc和Rr,通常情况下Rc和Rr相等。

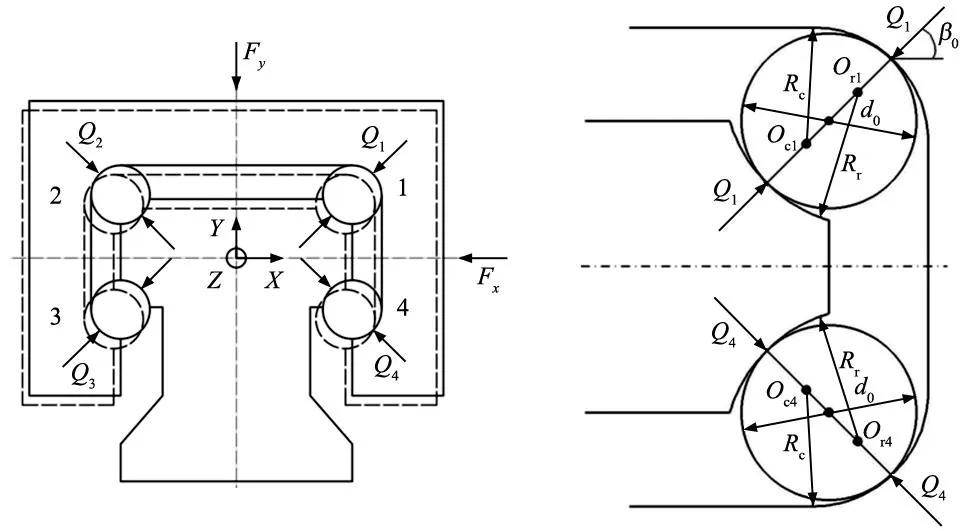
图3 滚动直线导轨副结构及受力图

当仅受预紧力P0时,滚珠的初始接触变形为δ0,通过分析得到Oci和Ori之间的距离s0为:

s0=Rc+Rr-d+δ0

(1)

式中:d表示没有安装滚珠时导轨沟槽与滑块沟槽之间的空间距离,d0为滚珠没有发生形变时的直径。在预紧力作用下,滚珠的变形δ0为:

δ0=d0-d

(2)

将滚珠与滚道接触视为弹性接触,根据Hertz接触理论[19],滚珠与滑块沟槽和导轨沟槽的接触力为:

(3)

式中:δi为滚珠的弹性变形,v1和v2分别为滚珠和沟槽材料的泊松比,E1和E2分别为滚珠和沟槽材料的弹性模量,μ为与刚度相关的赫兹系数,∑ρ为滚珠与沟槽接触的综合曲率。μ、∑ρ可以通过Hertz接触理论进行计算获得。将式(3)进行简化,得到:

(4)

式中:ξ描述了滚珠接触载荷Qi与弹性变形之间的关系,称为接触系数:

(5)

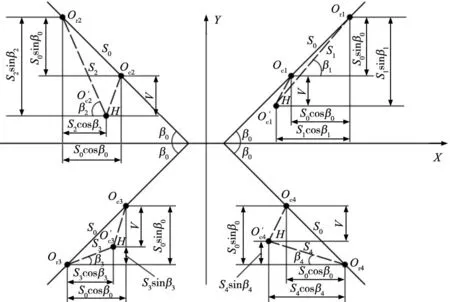
图5 滚动直线导轨位移与变形的几何关系

通过分析计算,得到各排滚珠的弹性变形和接触角表示为:

(6)

(7)

将式(6)带入式(4),得到滚珠的接触载荷:

(8)

通过式(8)可知,接触载荷Qi是关于垂直位移V、横向位移H的函数。但是,随着位移的增大,滚珠可能会失去与滚道的接触,此时接触载荷Qi会逐渐减少到0,因此接触载荷V和H的分段非线性函数[11]。直线导轨内部对滑块总的作用力可简化为:

(9)

式中:n表示每一排滚珠的数目,FH和FV分别表示导轨内部对滑块的横向载荷和垂直载荷。

1.4 直线导轨的动态运动方程

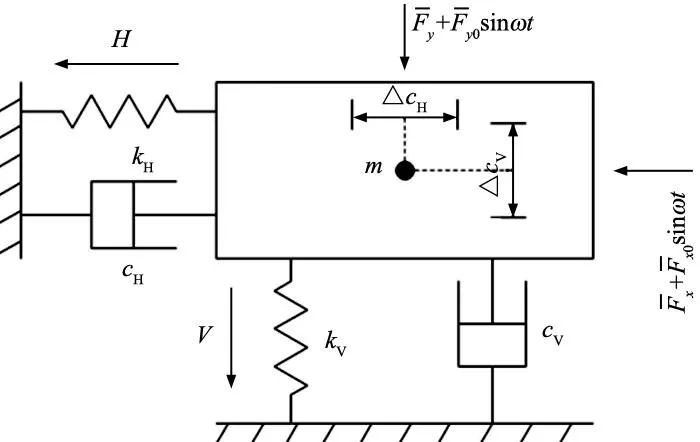
图6 直线导轨滑块二自由度动力学模型

由上述分析得到滑块的动态运动方程为:

(10)

由1.3节对直线导轨的载荷与接触变形分析可知,滚珠与滑块的接触刚度ki是滚珠弹性变形δi的非线性函数[11]。由式(6)可知滚珠弹性变形δi是关于水平位移H和垂直位移V的函数,因此ki同样为H和V的函数。式(10)中的kHH和kVV分别表示滑块系统因水平位移H和垂直位移V所产生的接触载荷,而等效刚度kH和kV为H和V的非线性函数[21]。为了简化计算,将kHH、kVV两项分别用滚珠对滑块的作用载荷进行表示[19]。由式(8)得表达式为:

(11)

将式(11)带入式(10)得到滑块系统的动态运动方程:

(12)

由式(12)可知,直线导轨的动力学方程比较复杂,且参数相互耦合,解析求解比较困难,因此利用龙格-库塔法进行求解,得到各个时刻直线导轨的动态响应值。

2 直线导轨几何参数不确定分析

本文用区间数对直线导轨的几何参数的不确定性进行表征,区间数DI是指任意一对封闭有界的实数[14]:

DI=[DL,DU]={D|DL≤D≤DU}

(13)

式中:上标L和U分别表示区间数的下限和上限。

区间数的中点Dc和半径Dw表示为:

(14)

因此,区间数还可以表示为:

DI=Dc+[-1,1]Dw

(15)

直线导轨动态性能受多个几何参数的影响,包括初始接触角β0、滚球直径d0、凹槽曲率rc和初始变形量δ0[11]。由于直线导轨零部件尺寸公差的存在以及在制造装配过程的随机因素影响,几何参数具有不确定性。因此,利用区间模型表示结构参数的不确定性。假设几何参数的不确定度为η,因此上述几何参数的取值区间为:

(16)

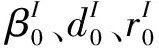
3 算例分析

3.1 直线导轨模型

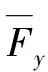
3.2 直线导轨动态响应分析

当各个设计参数在理想值时,采用文献[11]中的载荷条件,利用第2节中建立的动态模型计算滚动直线导轨的单自由度动态响应。图7为本文模型计算的直线导轨单自由度的动态响应值与文献[11]的对比结果。

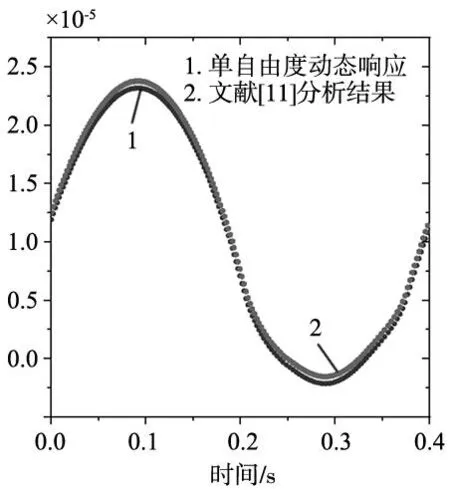
图7 动力学模型分析结果对比

从图7可以得到,在相同的载荷条件下,直线导轨垂直方向的动态响应结果基本一致。因此本文所建立的直线导轨动态分析模型的计算精度满足分析要求。

接下来,分别利用本文所建立的二自由度动力学分析模型对直线导轨的动态特性进行分析,得到了直线导轨的垂直位移和水平位移的动态响应。假设直线导轨几何参数[β0,d0,rc,δ0]的不确定度η=0.02,因此由式(16)可以得到几何参数的区间值。在几何参数区间分布情况下,通过二自由度动力学分析模型,得到直线导轨水平方向和垂直方向的动态位移响应。如图8所示,直线导轨水平位移和垂直位移的最大值、最小值以及理想值的分布情况,其中,图8a和图8b分别表示水平位移和垂直位移。对每个时刻,位移的最大值和最小值位于理想值的两侧。当直线导轨的精度等级为高精度时,其行走平行度公差为3 μm,从图中可以得到在一个运动周期中,直线导轨水平位移在公差范围之内约占运动周期的20%(其中上边界为32.5%,下边界为20%,取综合有效值20%),而垂直位移在公差范围之内约占运动周期的50%。

(a) 水平位移特性 (b) 垂直位移特性

由直线导轨受力情况可知,垂直方向载荷大于水平方向载荷,但是从图8可知,直线导轨水平方向的位移大于垂直方向,而且水平方向位移波动较大,一个周期内运行在公差范围之内的时间占比较小。主要原因是,由于垂直载荷的作用,第3列和第4列滚珠与滚道接触状态发生变化(图3所示),导致水平方向的等效刚度变小,而垂直方向等效刚度变大。

滚动直线导轨根据运动精度等级的不同,分为普通精度级、高精度级、精密级等,对应的行走平行度公差分别为5 μm、3 μm、2 μm。利用文中所述方法分别评估直线导轨的动态特性,导轨综合运动特性如表2所示。在相同载荷下,随着直线导轨精度等级的提高,允许的行走平行度公差逐渐减小,直线导轨水平方向和垂直方向运行在公差范围之内的时间占比逐渐减小。