一类延拓矩阵的半正定因子的扰动上界

孔祥强

（菏泽学院 数学系，山东 菏泽 274015）

一类延拓矩阵的半正定因子的扰动上界

孔祥强

（菏泽学院 数学系，山东 菏泽 274015）

利用行延拓矩阵的奇异值分解和极分解，得到了行延拓矩阵半正定因子的扰动界，并进一步讨论了特殊情形下的扰动界，且所得结论对于列延拓矩阵也是成立的.

行延拓矩阵；奇异值分解；极分解；半正定因子

延拓矩阵次酉极因子及半正定因子扰动界的问题是矩阵扰动分析的重要内容.有关次酉极因子扰动界的研究成果较多，而对半正定因子扰动界的研究成果相对较少.本文利用矩阵的奇异值分解和极分解的相关知识，得到了延拓矩阵半正定因子的扰动上界定理，并讨论了特殊情形下的扰动界.

1 几个定义和引理

定义1［1］设A∈Cm×n，称为矩阵A的行延拓矩阵.

定义2［1］设A∈Cm×n，称为矩阵A的列延拓矩阵.

定义3［2］若矩阵A∈Cn×n，满足AHA=AAH，则称A为正规矩阵；若满足AH=A，则称A为Hermite矩阵；若满足AH=A-1，则称A为酉矩阵.

定义4［3］设为Rk（A） 的扰动矩阵的奇异值分解分别为

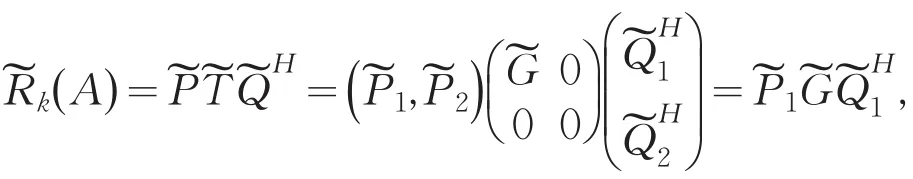
其中：U=（U1，U2）、V=（V1，V2）均为酉矩阵，U1∈Crm×r，V1∈Crm×r，∑1=diga（σ1，σ2，…，σ）r，σ1≥σ2≥…≥σr＞0；P=（P1，P2）、Q=（Q1，Q2）均为酉矩阵，均为酉矩阵

定义5［5］设，令，称的极分解，称Q为次酉极因子，H为半正定因子.

引理1［5］设，对进行奇异值分解（见定义4），则（1）

引理2［6］设为两个Hermite矩阵，E∈Cs×t，F∈Cs×t，若，则ΩX-XΓ=ΩE+FΓ有唯一解X∈Cs×t，且

2 主要结论

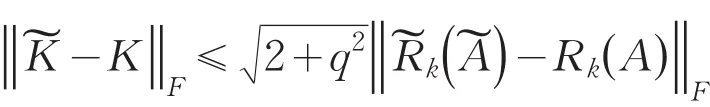
证明 对Rk（A）进行奇异值分解得，其中S=diag（μ1，μ2，…，μr），且μ1≥μ2≥…≥μr＞0.对进行奇异值分解得

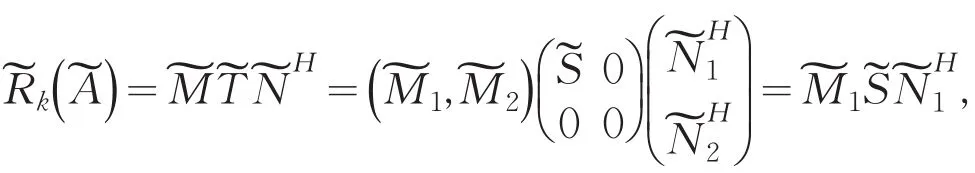
对R（kA）极分解得

令，则

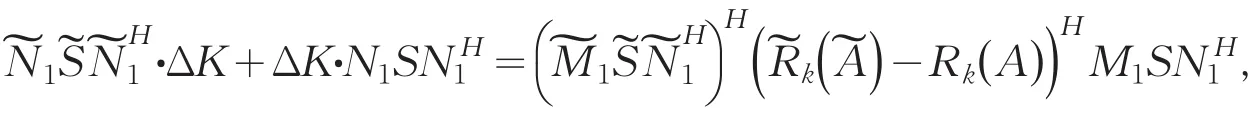
即

在式（3）两边右乘N1，得

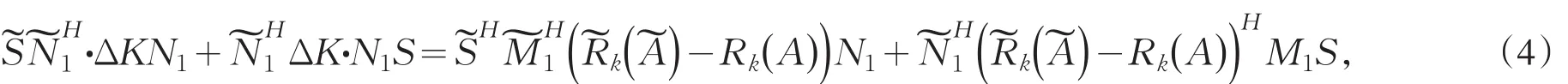
又

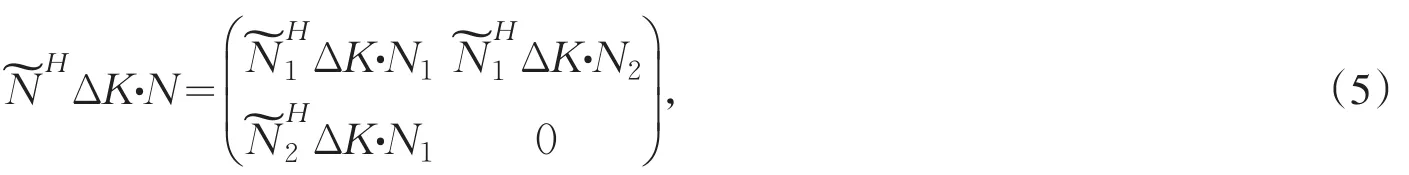
而

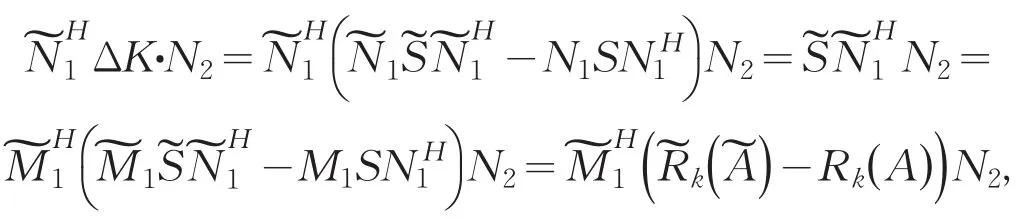
对式（4），由引理1、引理2得

由式（5），（6a），（6b），（7）可得

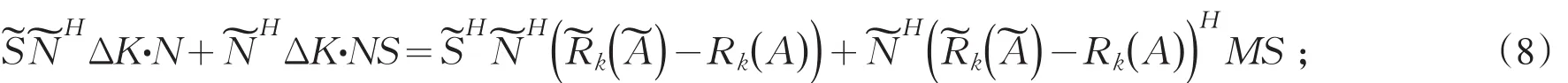
式（5）可写成

对式（8），式（9），再由引理1、引理2得

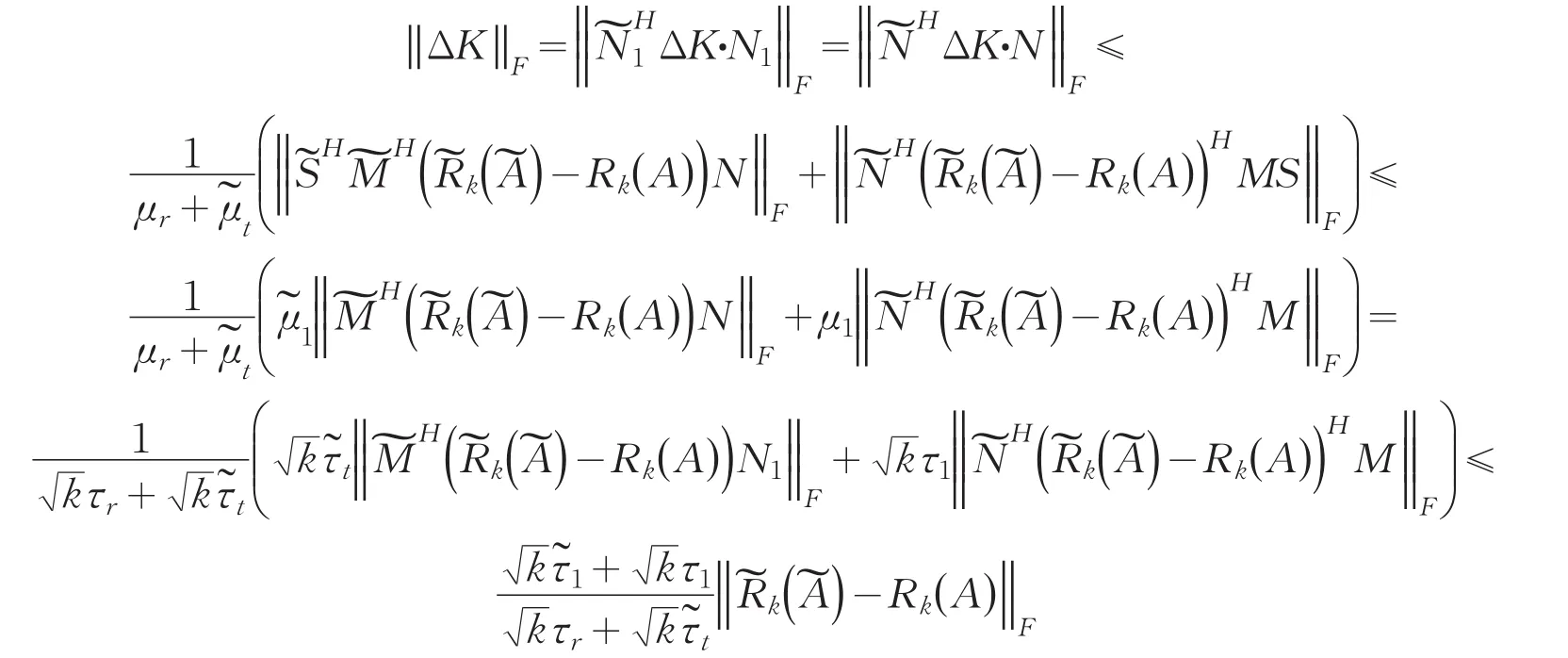
注 对于列延拓矩阵Ck（A），可利用转置，化为行延拓矩阵Rk（A），上述定理和推论也是成立的，不再赘述.

3 结束语

本文探讨了行延拓矩阵半正定因子的扰动界，分别讨论了r＜n、t＜n和r=t=n时的情形，得到了相应的的扰动上界定理，进一步完善了半正定因子的扰动界理论.

［1］邹红星，王殿军，戴琼海，等.延拓矩阵的奇异值分解［J］.电子学报，2001，29（3）：289-292.

［2］蒋正新，施国梁.矩阵理论及其应用［M］.北京：北京航空学院出版社，1998.

［3］Bauer E，Fike C.Norms and exclusion theorems［J］.Numer Math，1960，2（1）：137-141.

［4］孙继广.矩阵扰动分析［M］.北京：科学出版社，2001.

［5］吴强.延拓矩阵Rayleigh商的近似奇异子空间［J］.西南师范大学学报，2010，35（3）：19-22.

［6］Li R C.Relative perturbation theory：Eigenvalue and singular value variations［J］.SIAM J Matrix Anal&Appl，1998，19（4）：956-982.

Perturbation Upper Bounds for Positive Semi Definite Factors of a Class of Extension Matrix

KONG Xiangqiang

（Department of Mathematics，Heze University，Heze 274015，China）

By using the singular value decomposition and the polar decomposition of the extended matrix，the research obtains the perturbation bounds for the positive semi definite factors of the row extension matrix.It further discusses the perturbation bounds under special conditions.The conclusionis suitable to the column extension matrix.

row extension matrix；singular value decomposition；polar decomposition；positive semi definite factor

O 241.6

A

1674-4942（2016）02-0119-04

2016-02-27

2015年山东省教育科学“十二五”规划重点资助项目（2015GG696）；2016年菏泽学院教学改革重点课题项目（201610）