双质体振动设备主要参数的选择与计算

张亦工，韩成年，张亦农（. 鹤壁市质量技术监督检验测试中心，河南鹤壁 45800；. 深圳清欣机电设计室，深圳 5809；. 沃盛咨询（深圳）有限公司，深圳 5809）

双质体振动设备主要参数的选择与计算

张亦工1，韩成年2，张亦农3
（1. 鹤壁市质量技术监督检验测试中心，河南鹤壁 458030；2. 深圳清欣机电设计室，深圳 518019；3. 沃盛咨询（深圳）有限公司，深圳 518019）

对双质体振动设备的激振力、质量比、频率比、激振频率、固有频率等动力学参数进行了分析，提出了选择范围和计算方法；并探讨了振动设备确定参振体质心位置的必要性及方法，以及如何防治参振构件弯曲振动引起的危害。

双质体；激振力；质量比；频率比；激振频率；固有频率；质心；弯曲振动

双质体振动设备是由两个参振质体（工作质体和激振质体）组成的振动系统，其力学模型如图1所示。图中，工作承载体（工作质体）也称上质体，激振器（激振质体）也称下质体，上、下质体之间由主振弹簧联接，组成主振系统；该主振系统通过隔振弹簧与基础相联，整体组成隔振系统。图1所示为双质体振动设备一种常见的结构型式，例如铸造生产中的大型双质体固定式振动落砂机。双质体振动设备的另外一种结构型式则是上质体为激振质体，下质体为工作质体，例如电磁振动给料机、双质体惯性振动给料机、振动活化给料机。根据工艺结构要求，双质体振动设备的工作质体和激振质体也可分别通过隔振弹簧与基础相联。

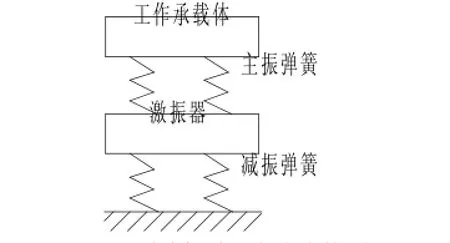
图1 双质体振动设备力学模型

常见的双质体振动设备动力学特性为线性近共振型，其动力学参数应包括：振动质体的计算质量及质量比，主振弹簧刚度及主振系统的频率比，隔振弹簧刚度及隔振系统的频率比，振动系统所需激振力及激振功率，以及传递给基础的动载荷等。本文仅对双质体振动设备所需激振力、质量比、频率比，以及激振频率和固有频率等动力学参数进行分析和计算，并对参振体质心位置及参振构件弯曲振动问题进行探讨。

1 激振力

振动设备所需激振力是参振质量在加速度下作简谐运动应有的强制力，在数值上应为弹簧回复力、外阻力、内阻力和参振体惯性力的代数和。求出振动系统所需激振力的大小，以配备有足够功率的激振器。

1.1 单质体振动系统激振力

文献[1]对直线振动的微分方程（二阶常系数齐次线性微分方程）求解，其特解为稳态运动方程，即有阻尼、强制振动的质量代数方程。对其求一次导数和二次导数，得到激振力精准计算式：

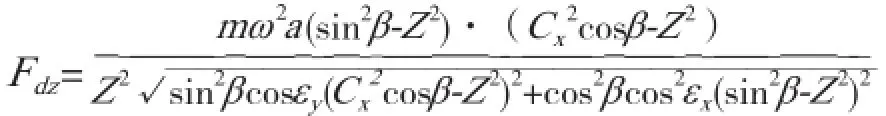
式中, Fdz为单质体振动系统激振力，N；m为参振质量，kg；ω 为激振频率，ω=2πn/60（r/s）；a为振幅，m；β 为振动方向角，°；Cx为隔振弹簧横向刚度系数；Z 为隔振频率比；εy、εx为激振力与位移分别在垂直和水平方向上的相位角差

1.2 举例

图2所示为单质体自同步惯性振动给料机结构简图。其中，给料机槽体质量m=500 kg，振动电机转速n=1 430 r/min，振动方向角β=30 °，取减振频率比Z=6，隔振弹簧横向刚度系数Cx=0.2，相对阻尼系数b=0.05，槽体振幅a=2.5 mm，求所需激振力大小。

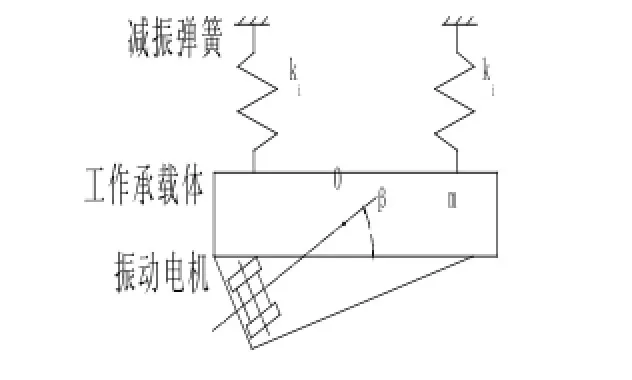
图2 单质体自同步惯性振动给料机结构简图

激振频率：ω=（2π×1 430）/60=149.7(r/s )

选用两台振动电机，每台振动电机功率1.1 kW，激振力20 000 N，质量86 kg。包括振动电机在内的参振质量为m=672 kg，重新精准计算所需激振力为Fdz=37 545 N。两台振动电机的激振力为2×20 000 N＞37 545 N，激振力和电机功率足够。

激振力简便计算式：Fdb=amω2

将有关数值带入得：

Fdb=0.002 5×672×149. 72=37 649（N）

两台振动电机的激振力为2×20 000 N＞37 649 N。

精准式与简便式的计算结果仅相差0.28%，可忽略不计。因此，设计单质体振动设备采用简便式计算激振力即可。

1.3 双质体振动设备激振力

文献[2]对双质体直线振动的微分方程求解，其特解为稳态运动方程，即有阻尼、强制振动的质量代数方程，对其求一次导数和二次导数，得到激振力精准计算式：

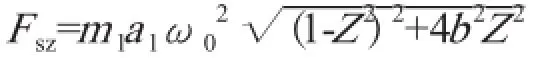
式中， Fsz为双质体振动系统激振力，N；m1为工作承载体质量，kg；a1为工作承载体振幅，m；ω0为主振系统固有频率，r/s；Z 为主振系统频率比，Z=ω/ω0；b 为相对阻尼系数。

1.4 举例

图3所示双质体惯性振动给料机结构简图。其中，给料机槽体质量m1=500 kg，槽体振幅a1=2.5 mm，振动电机激振频率ω=149.7 r/s，主振系统频率比Z=0.9，相对阻尼系数b=0.05。

图3 双质体惯性振动给料机结构简图

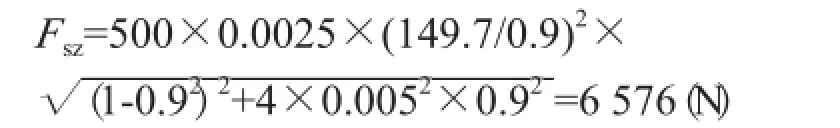
选用1台振动电机即可，振动电机激振力20 000 N，功率1.1 kW，质量86 kg。

激振力简便计算式：Fsb=a1m1ω02（1-Z2）

将有关数值带入得：

Fsb=0.0025×500×(149.7/0.9)2×(1-0.92)=6 568（N）

两式相差0.12%，可忽略不计。因此，设计双质体振动设备采用简便式计算激振力即可。

振动电机选定后，须将激振质体质量计入，用下式进行校验：

F=amω02（1-Z2）

式中， a为相对振幅，mm。a=a1+a2；a2为激振质体振幅，mm；m为计算质量（也称诱导质量），kg。m=m1m2/(m1+m2); m2为激振质体质量，kg。

已知，振动电机质量86 kg，电机安装底座质量60 kg，激振质体振幅a2=8 mm。

即：a= 2.5+8=10.5（mm），m2=86+60=146（kg） ，m=500×146/(500+146)=113（kg）

则：F=113×0.0105×(149.7/0.9)2×(1-0.92)= 6 233（N）

计算结果，F＜Fsb，校验通过。

设计中，振幅根据振动工艺选取，常用激振力

用精准式计算所需振动电机激振力：为振动电机最大激振力的70%～80%，使振幅有较大的调节余量，同时延长电机寿命。

从上式的计算中看出，同样规格的给料机和槽体振幅，双质体振动系统比单质体振动系统节省能量。

2 质量比

双质体振动设备的参振质量由驱动装置（激振质体）质量m2与工作承载体（工作质体）质量m1组成，两者的质量比为m2∶m1。

参振质量与振幅的关系为：

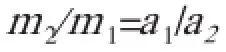
对双质体振动设备而言，参振质量m1、m2之间的调整变化，振幅a1、a2成反比例相应变化，激振力大小不变。

表1列出几种振动设备的质量比数据。主振弹簧为螺旋弹簧时，变形量大，质量比取值较小（0.1～1），工作承载体振幅较大。当主振弹簧为板弹簧或橡胶弹簧时，其变形量较小，质量比取值较大（1～1.5），工作承载体振幅较小。当工作承载体振幅要求较小时，使用板弹簧，质量比也可以取得较小。

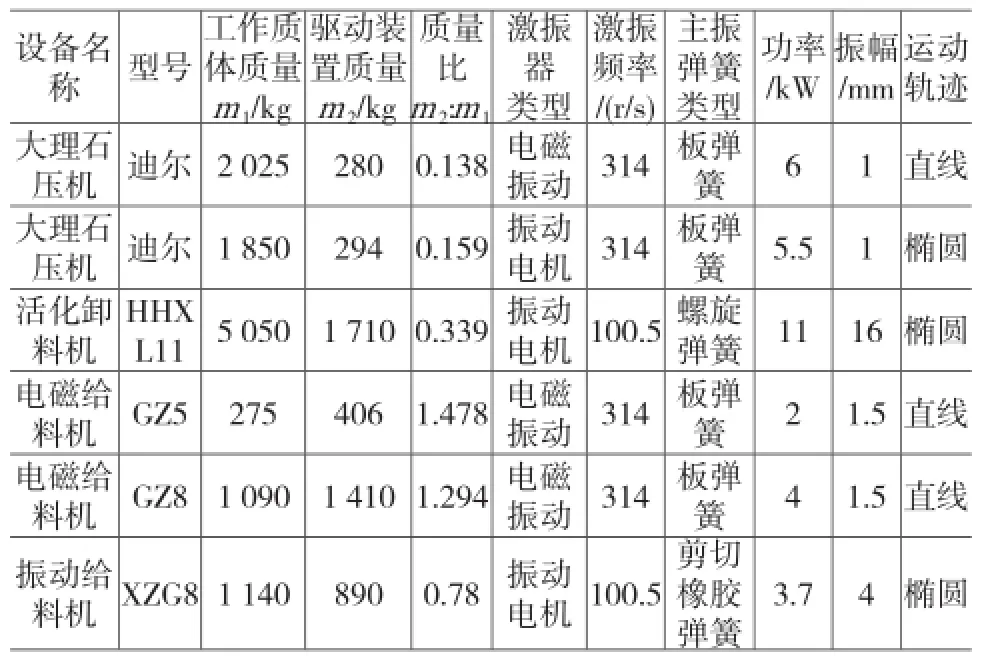
表1 几种振动设备的质量比

根据工作承载体的振幅、主振弹簧的类型、驱动装置的结构强度和安装空间，质量比有较大的取值范围。选择合理的质量比，可减轻参振质量，降低功率消耗。

在负载状态下，工作承载体的质量还应包含物料或其他载体的质量。工作时物料在振动，物料的质量以结合质量计入，通常取物料质量的20%～30%。对于轻型振动设备，一般可按空载计算；对于振动给料机、振动落砂机一定要计算物料的结合质量；振动料斗、振动活化给料机具有破拱能力，工作承载体的质量则不仅要计算物料结合质量，还要考虑仓压。

3 频率比

振动设备的频率比Z为激振频率ω与系统固有频率ω0之比：Z=ω/ω0。

频率比Z也称调谐值（工作点），是重要的动力学参数，以此衡量振动设备在何种状态下工作，并用于计算弹簧刚度、激振力，以及振幅的幅值。

当激振频率ω接近或等于固有频率ω0时，Z=ω/ω0→1，动力放大系数远大于1，用小的激振力即可获得较大的振幅。振动系统因存在阻尼，最大振幅不是在共振点处，而是略低于共振点的位置（ω/ω0略小于1），即低临界近共振点处。双质体振动系统即属于这一类型。

当激振频率ω远小于固有频率ω0时，Z=ω/ ω0→0 ，动力放大系数为1，弹簧的刚度很大。单质体振动系统即属于这一类型，激振器与工作承载体之间直接连接，相当于主振弹簧刚度无穷大。

当激振频率ω远大于固有频率ω0时，Z=ω/ ω0→∞，动力放大系数趋近于0，失去放大作用，弹簧刚度很小。隔振弹簧按此原则设计计算。

主振弹簧在低近共振状态下工作，频率比越接近1，系统所需的激振力越小，阻尼对振幅的影响越灵敏，系统的稳定性越差。振动设备的频率比一般选取0.85～0.95，在低近共振点处工作。

双质体振动设备的频率比通常是指主振系统的频率比，一般靠经验选取，如GZ型电磁振动给料机的频率比为0.9；振动活化给料机频率比为0.85～0.92，用于大料仓取小值，用于小料仓取大值；振动筛取0.85；振动输送机取0.9；当主振弹簧采用橡胶剪切弹簧时，频率比取1.1。

振动设备的隔振系统一般在远超共振状态下工作，取频率比Z=6～8，以尽量减小传递给基础的动载荷。

4 激振频率与固有频率

振动设备的激振器参数，主要包括激振力、激振频率和激振功率。

当采用振动电机或其它惯性激振器作为激振源时，其激振频率ω是由电机转速n换算的角频率：ω= 2πn/ 60 r/s。

激振频率根据振动设备的工艺、结构，以及振幅的大小要求选择。不同用途的振动设备选用不同的激振频率和振幅，例如，采用低频大振幅或者高频小振幅。

激振频率ω选定后，根据频率比Z确定固有频率ω0（见表2）。

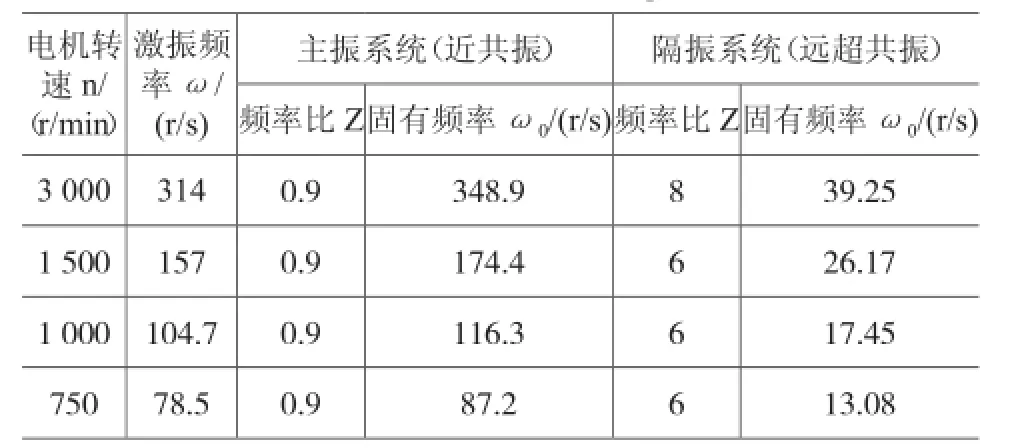
表2 固有频率ω0

固有频率ω0用于计算弹簧刚度：或 k=mω2/Z2。

式中， k为弹簧刚度，N/m；ω为激振频率，r/s；m为参振质量，在计算主振弹簧刚度时，m为计算质量（或称诱导质量），kg；在计算隔振弹簧时，m为工作质体与激振质体的质量和，kg；Z为频率比，计算主振弹簧刚度，取0.85～0.95；计算隔振弹簧刚度，取6～8。

当激振频率、频率比和参振质量确定后，即可计算出弹簧刚度。根据所需弹簧刚度进而进行弹簧设计，确定弹簧参数及弹簧数量。

5 质心

对于振动设备的参振质体，必须计算其质心位置，以确定激振器的安装位置和方向。

振动给料设备，具有直线振动轨迹或椭圆振动轨迹，通常用振动电机作激振源，激振力作用线必须通过槽体（工作承载体）质心，形成槽体的平面平移运动。否则产生附加力矩，以质心为支点，形成摇摆振动，增加功率消耗；槽体两端的振幅不相等，设备上各点对物料的作用力不同，物料运行平稳性差，物料运动速度不一致，严重时会形成物料堆积。

对于直线振动+扭转振动轨迹的垂直振动输送机，设备质心要处于垂直轴线上，两台交叉安装的振动电机质心应以垂直轴线为对称，且两电机质心连线应与垂直轴线垂直且相交。

对于采用振动电机激振的双质体长距离振动输送机，主振弹簧支点多，可以不考虑输送槽的质心问题，但振动电机的激振力作用线还是要通过平衡质量和安装支架的组合质心。双质体振动活化给料机主振弹簧较多，也应按此设计。

摇摆振动筛，能提高筛分效率。激振力对质心形成力矩，使筛体摇摆振动。

振动设备在某一方向结构具有对称性（如给料机在横向为对称结构），质心一定在其对称轴上，只需计算非对称方向结构（如给料机的纵向结构）的质心位置即可。简便的方法是先计算给料机槽体（工作承载体）的质心，将激振器质心置于过槽体质心的直线上，直线与水平线的角度（振动方向角）按需要确定。文献[3]、[4]对给料机槽体质心与激振器质心如何配置进行了阐述。在设备横向则要求激振器合力作用线与对称轴线重合。

质心位置用理论力学方法计算，将整个设备放在直角坐标系内，计算每个零件的质心坐标和质量，列出质心计算表。将零件编号、质量mi、坐标值（xi，yi）、一次矩(mixi、miyi)写入表中，按下式计算出设备质心的坐标(XC，YC)：

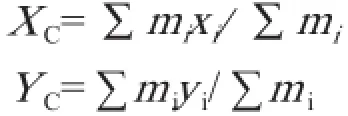
某些CAD绘图软件，如CAXA-电子图版，具有计算质心的功能，点击任意图形能自动显示质心位置及参数，快捷准确，省去繁琐的计算过程。

质心计算的繁琐、设备制造的误差、槽体中物料的质量难以准确计算等等因素，使得实际质心位置都存在一定误差。一般振动设备都有附加力矩，只是大小不同而已。根据给料机设计经验，激振力作用线与质心的偏心距误差在±4 mm范围内，设备都能正常运行。

对于倾斜直线振动的振动给料机，激振力作用线一般置于槽体质心的后方3～5 mm处。给料机工作时，料仓仓压和槽体内物料质量，将使设备与物料的组合质心后移，正好与激振力作用线重合。

6 弯曲振动固有频率

振动设备的工作承载体（例如给料机或输送机槽体）作为承载物料的构件，并非完全是刚体，实际上可以看作是一个弹性体，因而，每一个参振构件都有自己的固有频率。这是一种物理属性，与参振构件是否处于振动状态无关。

当参振构件固有频率与激振频率接近时，对于较长的工作承载体将会出现弯曲振动，这种弯曲振动在波峰顶与波谷底的振动方向角和振幅不同，表现为输送槽中物料在整个长度方向上输送速度的不一致性。有的部位运动快，有的部位运动慢，有的部位物料打转，不往前行，造成输送堵塞。如果槽体本身形成共振，则设备运行不平稳，槽体构件加速损坏。

工作承载体结构中的各构件质量、形状、大小、材质和刚度的不同分布，形成不同阶次固有频率和共振振型。

当构件受到外界某个特殊频率振动的扰动时，它会随着振动，且振幅越来越大，而达到最大振幅值。而它对于这个特殊频率以外的其它频率扰动，它也许也会随之振动，但不会振幅越来越大，达到最大振幅。

每一个构件有无数阶固有频率，对于较长工作承载体构件（如输送机槽体），通常计算最低的1～3阶的弯曲振动固有频率或实测结构动力特性模态参数，作为特殊的频率界限。

输送槽通常是由钢板弯曲成型的较长构件，看作是一种支承在弹性支座上的简支梁结构，承受均布载荷，其弯曲固有频率的计算式[5]：

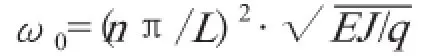
式中,ω0为构件固有频率，r/s；n为阶数，1、2、3、……；L为构件长度，m；E为材料弹性模数，N/ m2（kg.m/s2.m2）； J为断面惯性矩，m4；q为单位长度质量，即线密度，kg/m。

在进行槽体结构设计时，须使ω0计算值与所选择的激振频率错开（50%以上），不能与其重合，避免引起槽体共振。

当一阶弯曲固有频率远大于激振频率时，能提高构件整体刚度；激振频率可大于1阶，小于2阶、3阶的固有频率（相互错开50%以上）；输送槽的质量在整个长度上要均匀分布；导向杆、主振弹簧在整个长度上均匀布置；隔振弹簧在整个长度上均匀布置。

一旦出现弯曲振动，可在槽体薄弱部位加固；有针对性的设置支点；减小激振力；增加配重；完善结构动力特性，使设备平稳运行和延长使用寿命。

7 结论

双质体振动设备具有节能的优点，其成败主要取决于设计阶段的准确性和合理性，取决于各主要参数的选择和计算。设计中，振动参数需要凭经验选择，并要经过定量计算，进行校验，才能提高设备运行的可靠性。

[1] 韩京燕,韩成年. 单质体振动设备激振力和振幅的计算[J].矿山机械，2001(1):49-54.

[2] 电磁振动给料机编写组.电磁振动给料机[M].机械工业出版社，1973.

[3] 李凤国,韩京燕,韩成年.直线振动设备的重心和参振质量计算[J].中国铸造装备与技术，1999(2):50-53.

[4] 韩京燕,韩成年. 直线振动设备的激振器位置简便确定法[J].矿山机械,2000(10):47-48.

[5] 闻邦椿,刘风翘,刘杰编著.振动筛、振动给料机、振动输送机的设计与调试[M].化学工业出版社，1989.2.

[6] Francis S. Tse, Ivan, E. Morse, Rolland T. Hinkle. Mechanical Vibrations Theory and Applications[M]. Aliyn and Bacon inc, 1978.

Selection and several parameters of double body vibrating equipment

ZHANG YiGong1，HAN ChengNian2， ZHANG YiNong3
（1.Quality and Technical Supervision inspection center of Hebi city of Henan province, Xinxiang 458030,Henan,China; 2.Shenzhen Qingxin machinery& electrical design workshop,Shenzhen 518002,China; 3.WMGS consulting (Shenzhen)Co., Ltd., Shenzhen 518002,China)

This article is mainly to analyze the principle of energy saving about Double Body Vibrating Equipment and to list the selection range and calculation method of excitation force and mass ration frequency ration, excitation frequency and natural frequency; to determine the necessity and the calculation method of the mass ration; to study the harm of blending vibration and how to reduce the harm, the calculation method about the bending natural frequency, to select the excitation frenquency with staggered and to avoid the resonance.

excitation force;mass force;excitation frequency;natural frequency;center of mass;blending vibration

2016-03-28

稿件编号:1603-1311

张亦工（1974—），女，工程师，主要从事设备检测、计量检定工作.

TG234；

A；

1 006-9 658（201 6）06-0068-05

10.3969/j.issn.1 006-9 658.2016.06.021