“整体观”视角下的函数教学实践——以“一次函数与方程(组)、不等式”教学为例
2016-05-11江苏省如皋市吴窑初中夏红兰
☉江苏省如皋市吴窑初中 夏红兰
“整体观”视角下的函数教学实践——以“一次函数与方程(组)、不等式”教学为例
☉江苏省如皋市吴窑初中夏红兰
一次函数是在一次方程(组)、一次不等式之后学习的,不仅需要用到之前的数式运算、方程不等式的解法基础,而且可以从一次函数视角反观方程(组)、不等式,获得高观点下的结构认识,使学生对数学知识的理解更加深刻,特别是感受到数学知识、不同分支之间的关联与和谐一致.基于上述认识,笔者认真设计了八年级“一次函数与方程(组)、不等式”新课教学,取得较为理想的教学效果,本文整理该课教学设计,并跟进解读教学立意,提供研讨.
一、教学设计与意图解读
1.开课阶段
复习提问:一次函数y=kx+b的图像是什么?你在画一次函数的图像时有什么经验?
设计意图:通过引入问题揭示本堂课所研究的内容和一次函数的图像有关,并为后续学习做好铺垫.
2.新知探究
活动1:研究一次函数与一元一次方程的联系.
问题2:观察图像,找出图像与x轴交点的横坐标,并求对应的方程x+1=0的解.
问题3:讨论图像与方程的解之间的联系.
设计意图:通过实践、引导、对比,让学生总结出一次函数与一元一次方程之间的联系.
跟进练习1:
(1)平面直角坐标系中,直线y= kx+b与x、y轴的交点如图1所示,则关于x的方程kx+b=0的解为().
A.x=2B.y=2
C.x=-1 D.y=-1
(2)方程3x+1=7的解是__________,若函数y=3x+1的函数值是7,则相应的自变量x等于____________.
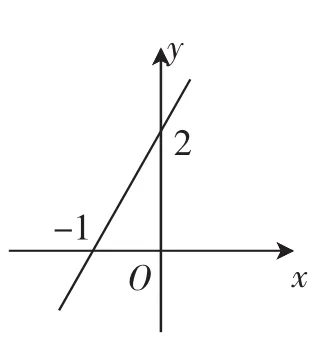
图1
(3)函数y=-x+2的图像如图2,并利用图像回答:
①当x=-1时,对应的y的值是____;
②当y=1时,对应的x的值是_____.
探究一次函数与不等式之间的联系.
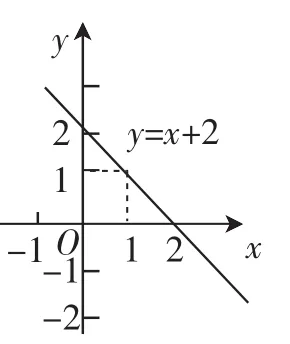
图2
活动2:画出函数y=2x-3的图像,接着观察图像并回答下列问题:
问题1:x取何值时,y=0?问题2:x取何值时,y>0?问题3:x取何值时,y<0?
教学互动:学生作出函数图像后观察,先小组内交流他们的解答,接着安排学生走上讲台全班展示,比如,以(1.5,0)为界,右边函数图像在x轴的上方,所以当x> 1.5时,y>0,左边函数图像在x轴的下方,所以当x<1.5时,y<0.据此引导学生总结一次函数图像与不等式之间的关系.
跟进练习2:
(1)一次函数y=kx+b(k,b是常数,k≠0)的图像如图3所示,则不等式kx+b>0的解集是().
A.x>-2 B.x>0C.x<-2 D.x<0
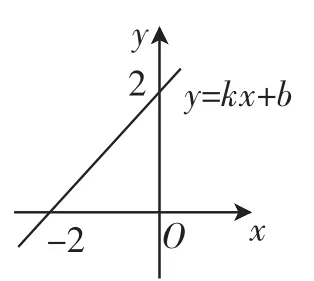
图3

图4
(2)如图4,一次函数y=kx+b的图像交坐标轴于A(-2,0)、B(0,3)两点,则不等式kx+b>0的解集是_____.
(3)已知函数y=kx+b的图像如图5所示,利用函数图像回答:
①方程kx+b=0的解是_______;
②不等式kx +b<0的解是________;

图5
③不等式-0.5<kx+b<2.5的解是_________.
活动3:在“活动2”中的平面直角坐标系中再画一次函数y2=x+3的图像,也就是在同一坐标系下出现两条直线y1=2x-3与y2=x+3,并解答下列问题:
(1)x取何值时,y1=y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1<y2?
预设互动:让学生在同一坐标中画出两条直线,观察图像找到当y1=y2、y1
引导学生确认如下发现:一次函数与一元一次方程、一元一次不等式之间有密切的关系,当函数值等于0时即为方程,当函数值大于或小于0时即为不等式.
跟进练习3:
(1)如图6,函数y=2x和y=ax+4的图像相交于点A(m,3),则不等式2x<ax+4的解集为______.
3.深化认识,研究“两直线交点”与二元一次方程组之间的关系
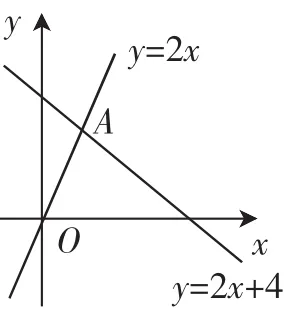
图6
活动4:探究一次函数与二元一次方程(组)的关系.
问题1:二元一次方程2x+5y=7可以变形为y= ________.(用含x的式子表示)
问题3:是否直线上任意一点的坐标都是它所对应的二元一次方程的解?
设计意图:这组问题主要是让学生看出二元一次方程与一次函数之间的关系,为接下来探究一次函数与二元一次方程组之间的关系预热一下.
教学预设:此时让学生画图、思考、发现两条直线与二元一次方程组之间的关系,为进一步归纳出方程组的解与两条直线交点提供必要的理解时间.
教学预设:引导学生进一步归纳出,从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值.
跟进练习4:
(1)以方程2x-y=3的解为坐标的所有点都在一次函数y=_____的图像上.
4.课堂小结
在黑板上画出如图7这样的小结,推介“藤蔓之美”的数学隐喻,让学生站在函数高处俯看之前所学代数式、方程与不等式.

图7
二、教学立意的进一步阐释
1.基于单元教学,让学生感受到数学的整体一致与和谐美妙
熟悉不同版本初中数学教材的同行应该知道,不少教材上对函数观点看方程、不等式的教学常常安排了2~ 3个课时,并且把上述课例中三个内容割裂开来,各个击破,大量练习训练,这样固然使学生对某一个知识的深化理解有一定的好处,然而学生在初次接触这样的教学内容时,缺少整体思维,不能感受到数学整体观,我们在一课中通过恰当的问题设计,引导学生依次思考了一次函数与一次方程,与不等式、方程组之间的关系,就如最后我们提供的那幅“藤蔓之美”的图形一样,学生不仅有了整体观,而且对不同知识或数学分支之间的整体一致与和谐美妙也有了更深的理解.顺便提及,《中学数学》(下)近年来刊发了大量以专家教师李庾南老师的课例为主的“单元教学”教学设计,值得我们深入理解和践行.
2.重视跟进训练,让学生在变式练习中巩固双基与深化理解
函数学习不仅需要理解概念生成的合理,更重要的是具体问题情境中能抽象出函数模型,在具体的数学习题中有函数解题的视角,所以在引导学生思考了一次函数与方程的关系之后,我们就及时跟进了一组变式练习,让学生在练习和解题中巩固双基,同时也是通过不同习题表征的呈现,让学生洞察问题的结构,达到数学概念或方法技能的“深刻理解”.这里的“深刻理解”也是指旅美学者马立平博士所指出的对数学知识的关联度、贯通度、广度、深度等方面的认知程度.
三、结束语
华东师大钟启泉教授指出,要从“教教材”走向“用教材教”,这是教师专业精进的标志之一.我们在上文基于数学整体观构造了一节“三个一次”的单元教学起始课,初步实践下来效果不错,但对教师课堂组织也提出了较高的要求,既可引导学生辨析难点,又要兼顾教学进度和教学时间,还有很多值得深入思考的话题,比如,单元教学的定位、划分,课堂时间如何把控等.这些都有待有识之士积极实践、反思提高.
参考文献:
1.李庾南,刘东升.藤蔓之美:从数式方程走向变量函数——以八年级“函数(第1课时)”教学为例[J].数学通报,2015(2).
2.钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).
3.章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013(6).
4.马立平,著.小学数学的掌握和教学[M].李士锜,吴颖康,等,译.上海:华东师范大学出版社,2011.
5.章建跃.课堂教学要注重数学的整体性[J].中小学数学(高中版),2013(5).
