基于UCB的短波认知信道选择算法
2016-05-08王董礼黄国策孙启禄王叶群
王董礼,黄国策,曹 鹏,孙启禄,王叶群
(空军工程大学 信息与导航学院,陕西 西安 710077)
短波具有超视距通信能力,开通架设方便,一直是重要的远程和机动通信手段,用途十分广泛。目前短波电台各自非合作的频率竞争和功率竞争不仅导致自身干扰冲突,而且污染了短波电磁环境,致使其他短波用户的可用频率减少和频谱质量下降[1],使得用户间冲突碰撞严重,频谱资源使用比较紧张。短波工业协会HFIA(High Frequency Industry Association)的研究表明,看似拥挤的短波频段存在数量可观的频谱空洞[2,3],因此,如何高效利用这些空闲的频谱资源具有重要意义。
认知无线电允许认知用户接入频谱空洞,减少冲突碰撞的同时实现频谱的高效利用。现有对认知无线电的研究主要集中在短波以上频段,文献[4]从动态频谱接入DSA(Dynamic Spectrum Access)的角度,提出将认知无线电应用到短波通信中。文献[5]分析验证了短波频段频谱空洞的可用性和稳定性,指出频谱空洞持续时间在数秒到数分钟间具有规律性,为DSA奠定了基础。文献[6]通过感知短波电磁环境,运用DSA策略实现抗干扰设计,避开干扰噪声较强的频率进行实时信道选择。因此,将认知无线电技术应用到短波通信中,可以使短波认知用户根据周围环境动态选择最佳工作频率,调整自身参数,优化通信效果。
动态频谱接入允许短波认知用户[7]在特定时间、地点使用空闲信道,根据强化学习(Reinforcement Learning)理论[8],通过对信道的探索和利用,动态接入空闲信道,能够在最大化自身传输机会的同时减少与其他用户的相互干扰。文献[9]使用强化学习中的UCB(Upper Confidence Bound)算法,验证其在短波环境下具有优良的性能。由于UCB算法学习时间较长,收敛到最优信道的速度较慢,影响其在短波环境下性能的提升。本文在文献[9]的基础上,建立适合认知背景的评价准则,提出一种改进的UCB算法,该算法借鉴权重驱动(Weight-Driven)算法思想[10],引入信道质量差异因子,根据探索学习结果动态调整探索信道数量和探索系数,能够快速收敛于最优信道,较原始UCB算法和随机信道选择算法具有较高的成功传输率和较低的累积接入损失。
1 系统模型
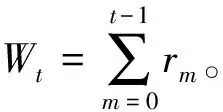
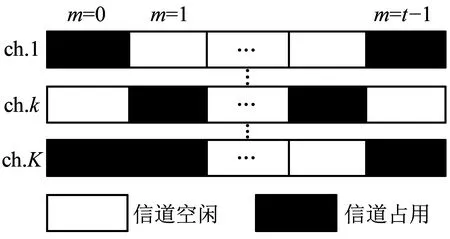
图1 系统的信道模型
2 UCB算法
2.1 UCB1算法
UCB算法是强化学习算法之一,是1995年由AGRAWAL R[13]提出的基于索引的算法,能够解决MAB中探索新臂以获得更多收益信息和选择已有收益最高的臂来获取最大利益之间的权衡问题。在认知无线电应用场景下,该算法不需任何信道先验信息,通过对历史决策行为和获得收益的学习进行决策,能够最大化认知用户的累积接入次数和时间[14]。根据强化学习理论[8],UCB算法分为探索(Exploration)和利用(Exploitation)两个阶段,该算法能够在探索学习的同时预测下一时隙最可用的信道,并根据利用阶段的接入结果更新相应信息,因此能够为短波认知用户选择最优信道提供依据。
UCB算法在每个时隙更新索引值Bt,k,Tk(t),并返回使该索引值最大的信道索引号k。索引值Bt,k,Tk(t)的计算方法为
(1)
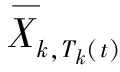
(2)
式中:am∈{1,2,…,K}为短波认知用户在第m时隙使用UCB算法选取感知的信道索引号;l{am=k}为逻辑表达式,当am=k时,其值为1,反之为0;Tk(t)为在前t个时隙内信道k被该算法选择的次数。
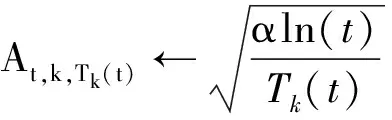
At,k,Tk(t)为索引值Bt,k,Tk(t)的置信因子,即
(3)
该UCB算法被称为UCB1算法,其中,α为探索系数,具体算法如下。
输入:K,a,{a0,r0,a1,r1,…,at-1,rt-1}
输出:at
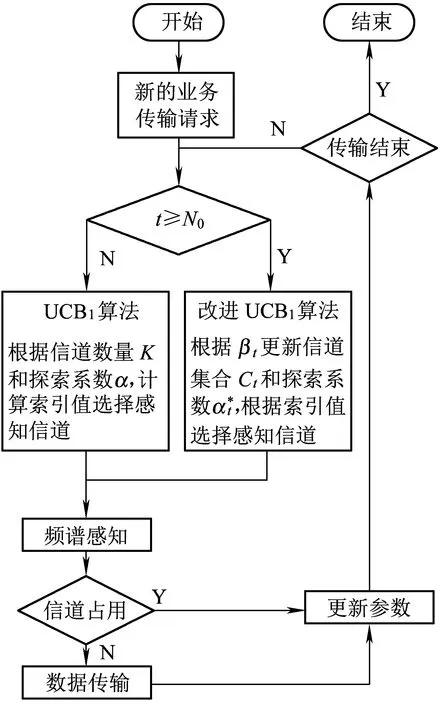
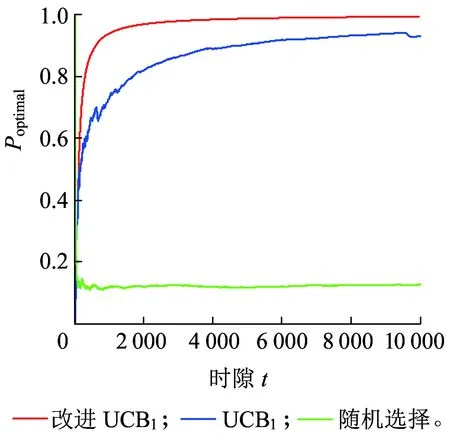
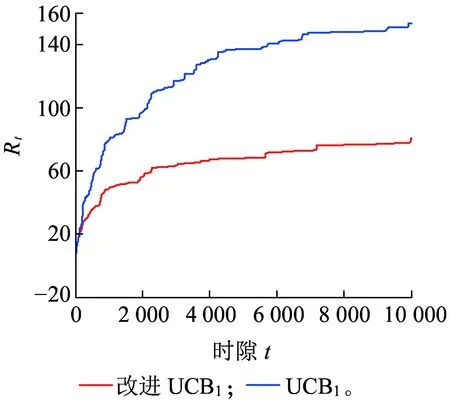
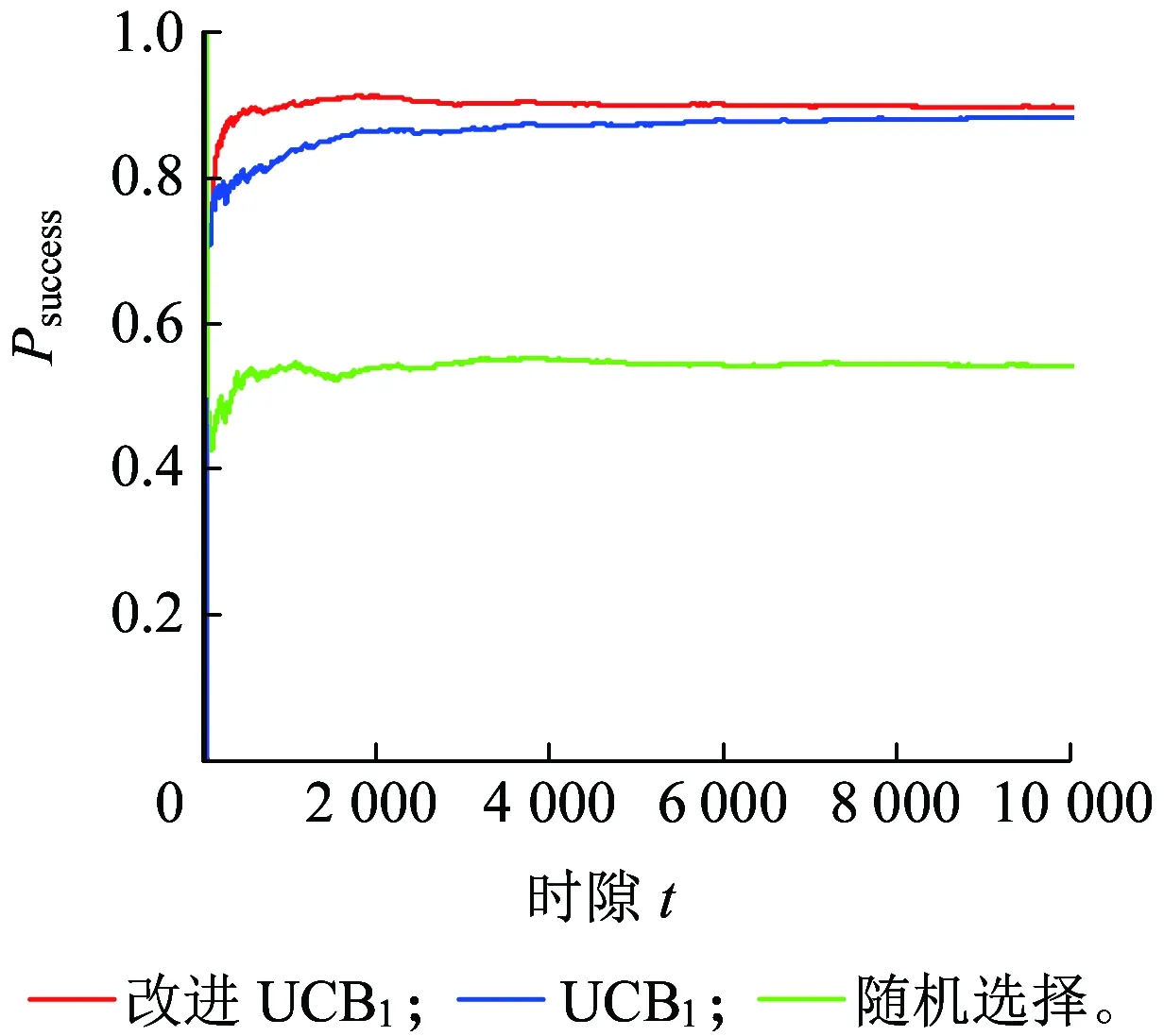
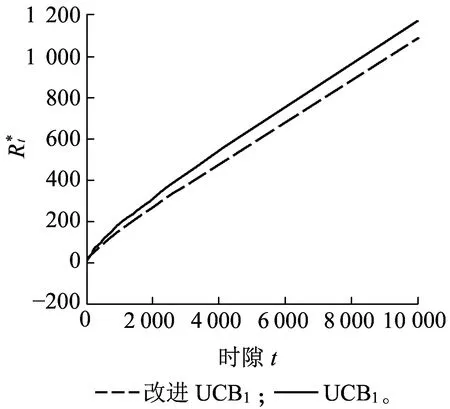
ift at=t+1 else at=arg maxk(Bt,k,Tk(t)) end if returnat 定义信道质量差异因子βt为 (4) (5) (6) (7) (8) 为避免由于学习不充分造成的信道误判,导致无法收敛于最优信道,陷入局部最优值,应当在进行可观的N0次接入后再进行信道数量缩减操作。改进UCB1算法的具体流程如图2所示,当有新的业务传输请求时,若t 图2 改进UCB1算法流程图 (9) 在机器学习领域,短波认知用户如果选择最优信道(即空闲概率最高的信道)进行数据传输,此时对其他短波用户产生干扰的可能性较小,因而可以使用最优信道选择比率Poptimal作为准则评估学习算法的性能。 (10) 同样,从机器学习的角度,如果短波认知用户每个时隙选择最优信道,则认为能够取得最佳性能。因此与最优信道选择策略相比,使用改进UCB1算法进行信道选择,短波认知用户的累积接入损失为Rt=tμmax-Wt,其中,μmax=max{μ1,μ2,…,μK}。因此,在t足够大时,短波认知用户的平均累积接入损失为 (11) 式中:θmax=max{θ1,θ2,…,θK}。 在短波中应用认知无线电,此时评估改进UCB1算法的准则与机器学习领域不同[9,16]。短波认知用户不关心选择的信道是否为最优信道,而是选择的信道在当前时刻是否空闲,因此最优信道选择比率Poptimal无法用来衡量认知背景下该算法的性能,此时用成功传输率Psuccess进行表征。 (12) 式中:Wt为短波认知用户进行信道选择后接入的累积收益。 在机器学习准则下,短波认知用户趋向接入最优信道,由于最优信道并非任意时刻空闲,非最优信道在未被占用时也能接入进行传输,因此累积接入损失Rt并未真实反映短波认知用户损失的传输机会。考虑机会式频谱接入OSA(Opportunistic Spectrum Access)策略,此时认知用户能够获得信道先验信息,只要信道组中所有信道并非完全被占用,短波认知用户就能接入未被占用的信道进行数据传输,最大化信道利用率。引入逻辑符号St表示信道组中信道状态的整体情况。 (13) (14) 图3为三种算法的最优信道选择比率Poptimal,由于随机信道选择算法为非学习算法,无法利用历史信息进行学习决策,所以其Poptimal最低,约为12.5%(即1/K);原始UCB1算法的Poptimal随时隙t增长并趋于稳定,在t=5 000时略高于90%,收敛速度较慢,在仿真时间内最高可达94.18%;而改进UCB1算法的Poptimal最高,由于该改进算法能够根据学习的信道情况主动缩减探索信道范围,调整探索系数,在t=620时Poptimal达到90%,收敛于最优信道的速度最快,并且随着时间的增长Poptimal趋于100%。 图3 最优信道选择比率Poptimal 因为随机信道选择算法的累积接入损失Rt较大,只给出改进UCB1算法和原始UCB1算法Rt的对比,如图4所示。由于所选信道并非任意时刻空闲,Rt反映了短波认知用户与其他短波用户产生冲突的可能,Rt越高意味着较最优信道选择产生的错误越多,产生冲突的可能越大,浪费的传输机会越多。从图4可知,改进UCB1算法具有更低的Rt,在t=104时仅为80.5,较原始UCB1算法减少47.56%,可见改进算法能够更好地找到最优信道,减少累积接入损失。UCB算法通过选择最优信道和周期性的探索其他信道,从而对信道情况进行更好的学习,因此在图4的累积接入损失Rt中会出现轻微的跳跃。 图4 累积接入损失Rt 图5为三种算法的成功传输率Psuccess,同样随机信道选择算法的Psuccess最低,约为54%;原始UCB1算法的Psuccess随时隙t增长并趋于稳定,在仿真时间内最高可达88.34%;而改进UCB1算法能够动态调整探索信道数量和探索系数,保留空闲概率较高的信道,因此其Psuccess最高,最高可达91.31%,并随时间增长逐渐趋于90%(仿真条件中信道最高空闲概率为90%)。由于该算法选择的最优信道中,并非每一时刻都是空闲,对比图3中的Poptimal可知,改进UCB1算法的Psuccess低于Poptimal,并且空闲概率较小的信道对成功传输率影响不大,通过剔除空闲概率较小的信道,在时隙t较小时,就能达到较高的成功传输率。 图5 成功传输率Psuccess 图6 对比OSA的累积接入损失 在短波中应用认知无线电,能够提高短波频段频谱利用率,减少冲突碰撞的几率。结合强化学习理论,本文提出基于UCB的短波认知信道选择算法,采用多种指标分别在机器学习和认知背景下验证算法性能。仿真结果表明,该算法能够有效提高信道接入成功传输率并降低累积接入损失,具有良好的通信效果。但是随着短波宽带技术的发展,在每个时隙只选择一个信道无法满足宽带传输的需求,因此如何利用UCB算法在每个时隙选择多个可用信道进行宽带传输是下一步研究的重点。 参考文献: [1]姚富强, 刘忠英, 赵杭生.短波电磁环境问题研究——对认知无线电等通信技术再认识[J].中国电子科学研究院学报, 2015, 10(4):156-161. YAO Fuqiang, LIU Zhongying, ZHAO Hangsheng. Study on the Issues of HF Electromagnetic Environment[J]. Journal of CAEIT, 2015, 10(2):156-161. [2]WILLIAM F. Summary: Wideband HF Channel Availability Working Group[R/OL]. http://www.hfindustry.com/meetings_presentations/presentation_materials/2015_feb_hfia/presentations/4-HFIAWidebandHF.pdf. [3]BRAM W. Wide Band HF UK Spectrum Utilisation [R/OL]. http://www.hfindustry.com/ca_meetings/presentation_materials/2015_feb_wb/2-WideBandHFSpectrumAvailability.pdf. [4]KOSKI E, FURMAN W N. Applying Cognitive Radio Concepts to HF Communications[C]// IET 11th International Conference on Ionospheric Radio Systems and Techniques. New York:IEEE Press, 2009:1-6. [5]闫建峰,郭锐,田骅. 基于认知的短波动态频谱孔洞率与时效性研究[J]. 舰船科学技术, 2011, 33(6):56-60. YAN Jianfeng,GUO Rui,TIAN Hua. Research on Spectrum Hole Probability and Effectiveness for a Given Period of Time of Dynamic Spectrum of HF Channel Based on Cognition[J]. Ship Science and Technology, 2011, 33(6):56-60. [6] ZHU Y C, WANG P, LU J X. A New HF Radio Prototype Based on Dynamic Spectrum Anti-Jamming Concept[C]// 6th International ICST Conference on Communications and Networking in China. New York: IEEE Press, 2011:955-958. [7]彭开志,刘进,王书诚.基于频谱检测的短波认知用户性能优化[J].铁道学报, 2012, 34(4): 57-63. PENG Kaizhi, LIU Jin, WANG Shucheng. Optimization of HF Secondary User Performance through Spectrum Sensing[J]. Journal of the China Railway Society, 2012, 34(4): 57-63. [8] SUTTON R S, BARTO A G. Reinforcement Learning[M].Cambridge:The MIT Press, 1998. [10] JIANG T, GRACE D, MITCHELL P D. Efficient Exploration in Reinforcement Learning-based Cognitive Radio Spectrum Sharing[J].IET Communications, 2011, 10(5):1 309-1 317. [11] ROBBINS H. Some Aspects of the Sequential Design of Experiments[J]. Bulletin of the American Mathematical Society, 1952,58(5): 527-535. [12]赵林靖, 苟俊杰. 基于MAB模型的多信道选择与接入算法研究[D]. 西安: 西安电子科技大学, 2014. [13] AGRAWAL R. Sample Mean Based Index Policies with O(log n) Regret for the Multi-armed Bandit Problem[J]. Advances in Applied Probability,1995,27(4):1 054-1 078. [14] JOUINI W, ERNST D, MOY C, et al. Multi-armed Bandit Based Policies for Cognitive Radio’s Decision Making Issues[C]// 3rd International Conference on Signals, Circuits and Systems (SCS). New York: IEEE Press, 2009:1-6. [15] AUER P, Cesa-Bianchi N, FISCHER P. Finite Time Analysis of the Multi-armed Bandit Problem[J]. Machine Learning, 2002,47(2-3):235-256. [16] ROBERT C, MOY C, WANG C X. Reinforcement Learning Approaches and Evaluation Criteria for Opportunistic Spectrum Access[C]// IEEE International Conference on Communications. New York: IEEE Press,2014:1 508-1 513.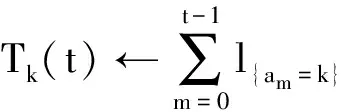
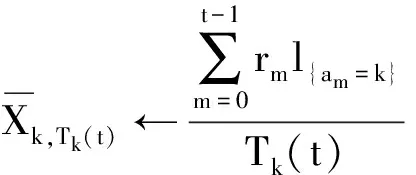
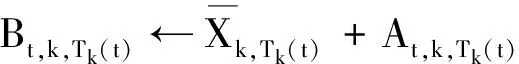
2.2 改进UCB1算法
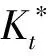
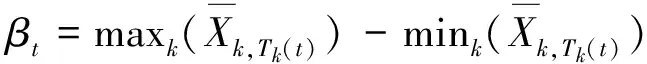
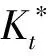
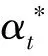
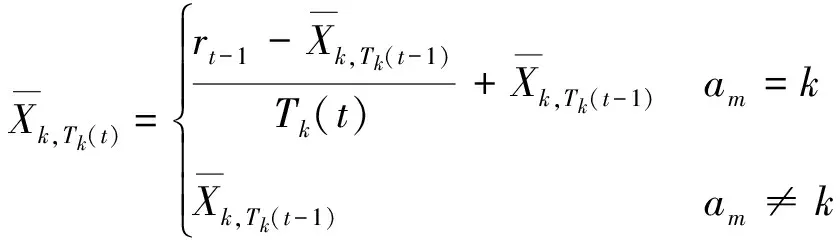
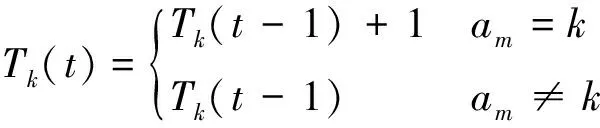
3 评价准则
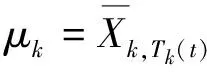
3.1 机器学习下的评价准则
3.2 认知无线电下的评价准则
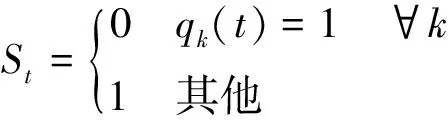
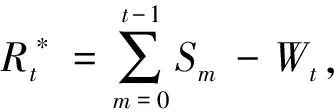
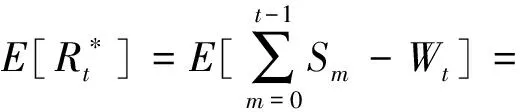
4 仿真分析
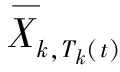
4.1 机器学习下的性能分析
4.2 认知背景下的性能分析
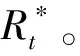
5 结束语
