收缩徐变对高铁混凝土拱桥变形影响的模型试验研究

张双洋，赵人达，占玉林，徐腾飞，杨 潇

(西南交通大学 土木工程学院，四川 成都 610031)

高速铁路客运专线行车过程中的安全性和舒适性，对轨道平顺度和铁路桥梁刚度提出了严格要求。钢筋混凝土拱桥具有刚度大、承载能力和跨越能力强等优点，在高速铁路大跨度桥型中具有明显优势。目前，国内外已建和在建的大跨度钢筋混凝土拱桥主要有：万县长江公路大桥、克罗地亚KRK1号桥、美国Colorado桥、澳大利亚Gladesvile桥、北盘江特大桥和南盘江特大桥。其中，北盘江大桥主跨445 m，建成后将成为世界同类桥梁之首。国内外学者对大跨度混凝土拱桥的极限跨径进行了探索，克罗地亚和日本分别就材料和施工工艺革新展开研究，国内桥梁学者也针对不同混凝土材料和矢跨比所能达到的极限跨径进行研究。跨径突破的主要难题是结构优化、自重减轻和施工方法的改进，通过对国内外大跨度混凝土拱桥施工方法的对比分析，北盘江大桥最终选择全桥范围采用劲性骨架，外包混凝土采用纵向分段、横向分环的施工方法，解决了施工过程中未成拱外包混凝土带来的材料自重问题。

大跨度混凝土拱桥的长期变形直接影响结构的安全运营，混凝土收缩徐变是大跨度混凝土桥梁长期变形的重要影响因素。文献[1-2]分别结合万县长江公路大桥和广西蒲庙大桥，对大跨度混凝土拱桥收缩徐变和施工工艺进行理论研究，提出大跨度劲性骨架混凝土拱桥收缩徐变效应的分析方法和施工方法，但在分析过程中未考虑混凝土收缩徐变随机性的影响。文献[3]对万县长江大桥进行缩尺1∶10的模型试验研究，研究主要针对桥梁的施工过程，未研究收缩徐变引起的长期变形和反推实桥变形。目前开展的拱桥模型试验研究[4-9]多数以刚桁架拱或提篮拱为背景，上承式混凝土拱桥较少，并且国内外已建成的大跨度钢筋混凝土拱桥中，公路桥梁居多，铁路桥较少，相关研究资料有限。

北盘江特大桥是目前世界上最大跨度的混凝土拱桥，首次在高速铁路客运专线上应用。混凝土的收缩徐变效应会使结构长期变形逐渐加剧，对高速铁路轨道的平顺性产生不利影响；大桥在施工过程中体系转化次数多，结构刚度与强度是逐步形成的，且该桥施工周期长、步骤多、混凝土龄期差别大，为确保施工过程安全并为后期轨道铺设提供技术支持，需要准确了解桥梁在施工过程及成桥后由混凝土收缩徐变引起的变形情况。国内外学者在进行大跨度拱桥收缩徐变分析时多基于现行规范的参数统一化模式，难以适应特定混凝土材料、结构形式和施工方法，因此，对大桥进行缩尺模型试验并合理预测结构的长期变形尤为重要。

国外学者开展混凝土收缩徐变方面的研究较早，得出具有代表性的计算模型为MC78模型、MC90模型、ACI209模型、GL2000模型和B3模型，这几种模型均是建立在试验均值基础上的半理论半经验模型[10]。文献[11-12]研究表明，GL2000模型和B3模型表现出的离散性较小，可以得到较好的预测效果并用于确定性分析，但B3模型需要先确定混凝土配合比。本文模型试验中的混凝土材料与原型存在差异，因此以GL2000模型作为混凝土收缩徐变的计算模型，对北盘江特大桥主拱圈模型进行9个时间工况的变形预测，并根据拱桥模型的预测结果反推原型长期变形情况，与原型考虑混凝土收缩徐变随机性的计算结果进行综合对比分析。

1 工程概况

沪昆高速铁路北盘江特大桥为主跨445 m、矢高100 m劲性骨架钢筋混凝土拱桥，拱轴系数1.6，矢跨比1/4.45。该桥拱圈高度为9.0 m，主拱圈截面采用单箱三室、等高、变宽的形式，其中，拱脚65 m范围内为18～28 m线性变宽，拱脚的变宽段由左右两个边箱的宽度变化来实现；左右两个边箱的宽度变化范围为3.5～8.5 m，主拱圈中间315 m范围为18 m等宽，由拱脚至拱顶方向，边箱底板厚度由110 cm变至85 cm，边箱顶板厚度由90 cm变至65 cm，中腹板为50 cm等厚，边腹板厚度由65 cm变至50 cm，中箱顶底板厚度均为60 cm，劲性骨架钢管规格为φ750×24 mm，图1为主拱圈拱顶及拱脚的截面尺寸，图2为主拱圈平面图，全桥外观效果如图3所示。

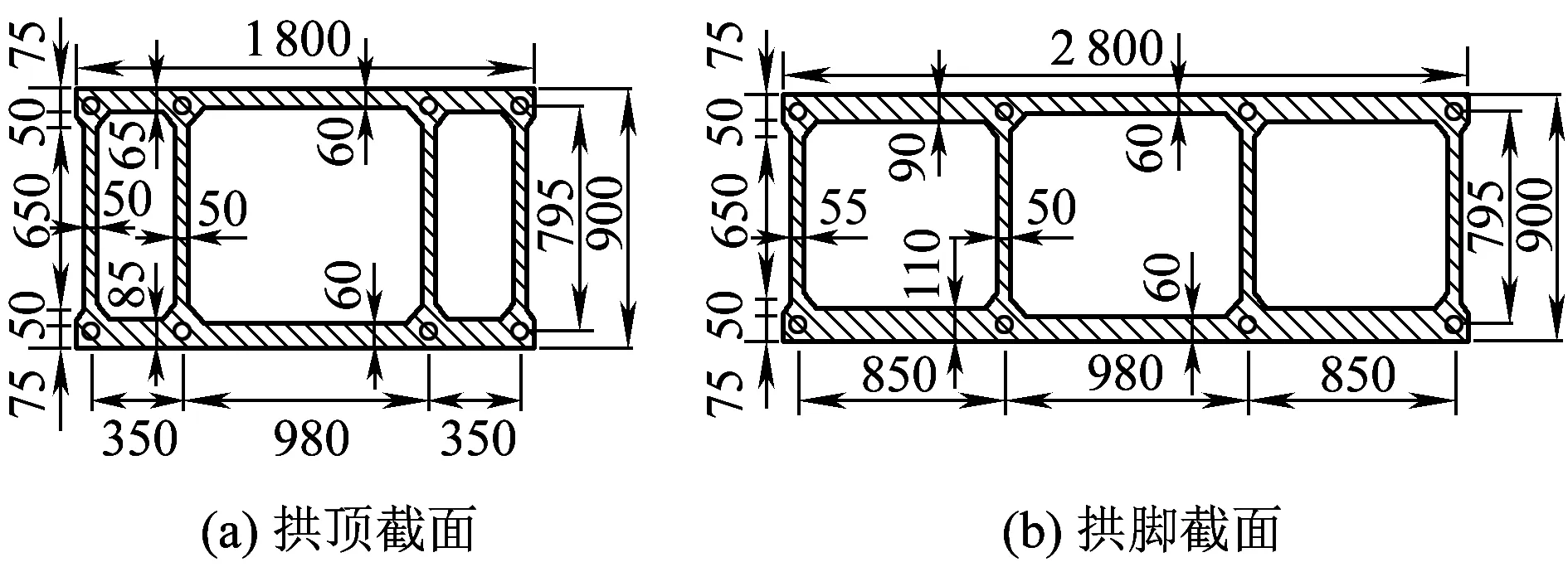
图1 拱圈截面(单位：cm)

图3 北盘江大桥效果图

图2 拱圈平面(单位：m)

2 模型试验

2.1 模型概况

本模型以北盘江特大桥主拱圈为原型，按照1∶7.5的比例制作，即几何相似常数为Cl=1/7.5；二者采用相同的材料，即材料弹性模量比CE=1，材料泊松比Cμ=1，按相似理论可以得出材料容重相似系数为Cγ=7.5，即模型材料的容重为原型材料的7.5倍。要保证模型桥满足原型受力和变形的相似关系，需要对模型桥施加6.5倍自重荷载。模型桥的恒载补偿以配重块加载方式实现，考虑到试验可行性，本模型桥以分布集中力的形式代替均布荷载实现恒载补偿，从而达到应力等效原则，即Cσ=1，相关参数的相似关系见表1。

表1 拱桥模型相关参数的相似关系

拱桥模型的骨架中心线线形为悬链线，计算跨度为59.33 m，拱轴系数1.6，矢高13.41 m。模型主拱圈上下弦钢管中心桁高1.07 m，主拱圈截面采用与原型相同的截面形式，拱座向内0.46 m为拱脚埋入段，骨架宽度沿桥轴纵向由3.65 m变至3.56 m，骨架变宽由外侧桁架片外倾实现；拱脚8.67 m范围由3.56 m变至2.24 m，变宽段同样由外侧桁架片外倾实现；拱顶42 m范围为2.24 m等宽。主拱圈劲性骨架由8根钢管及其横向连接系组成，拱桥模型的每个节段均设一榀横向连接系，长度均为1.31 m。拱桥模型的劲性骨架合龙状态和成桥状态外观如图4、图5所示。

图4 拱桥模型劲性骨架合龙状态外观图

图5 拱桥模型劲性骨架成桥状态外观图

劲性骨架钢管缩尺后的直径为100 mm，壁厚3.2 mm，考虑到直径100 mm制作难度较大，最后选择φ102×3.5 mm无缝钢管代替，主拱圈劲性骨架结构立面图和平面图如图6、图7所示。

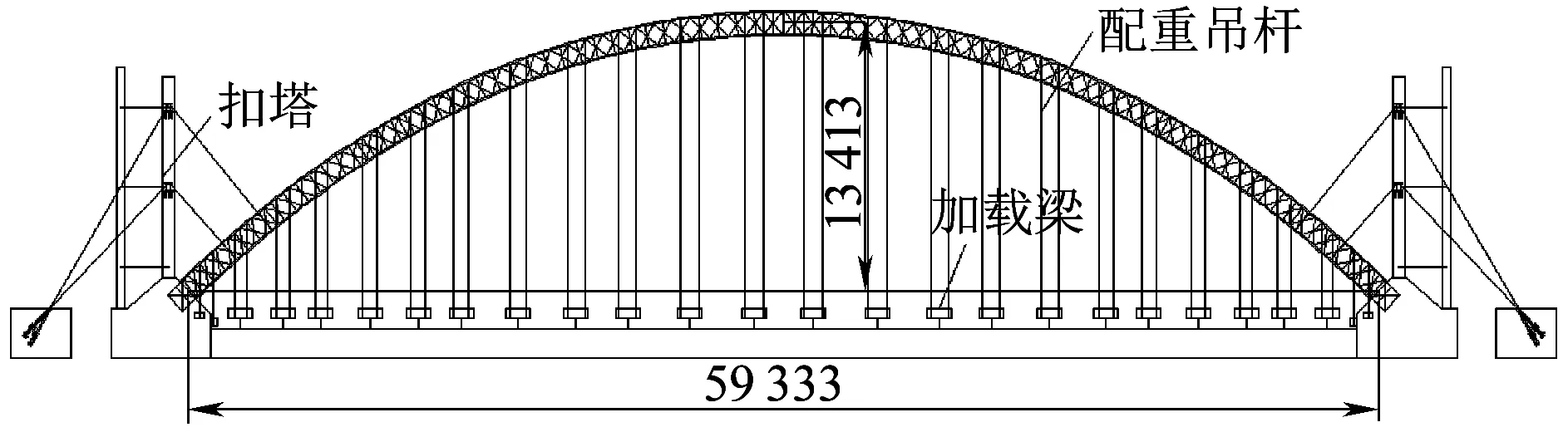
图6 拱桥模型劲性骨架立面图(单位：mm)

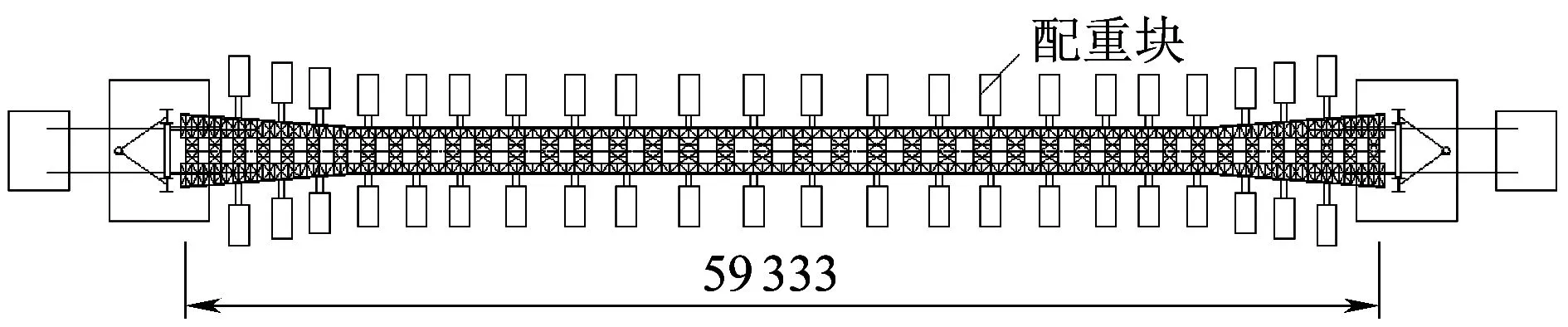
图7 拱桥模型劲性骨架平面图(单位：mm)

2.2 模型材料

根据模型设计原则，为了使拱桥模型最大程度与原型相似，本模型应采用与原型结构相同的材料制作，但由于材料购买与现场施工等条件的影响，对其中部分材料做了调整。

劲性骨架钢管经过缩尺后内径为94 mm，根据设计，管内材料为C80高强混凝土，其粗骨料粒径为5～20 mm，流动性较差，无法在拱桥模型的钢管内灌注，为保证管内材料的密实性，最终选择桥梁专用的高强自密实砂浆(CGM砂浆)作为管内材料，其性能见表2。

表2 CGM砂浆材料试验结果

拱桥模型的连接系和钢筋布置较密集，且外包混凝土的各个部位尺寸均较小，给施工带来不便。为满足外包混凝土施工的要求，将原型C60混凝土的粗骨料级配由原来的5～20 mm调整为5～10 mm，调整后的材料配合比及性能试验结果见表3、表4。

表3 C60细石外包混凝土配合比 kg/m3

注：掺合料为硅粉和矿渣粉，外加剂为减水剂；砂率42%，水胶比0.29。

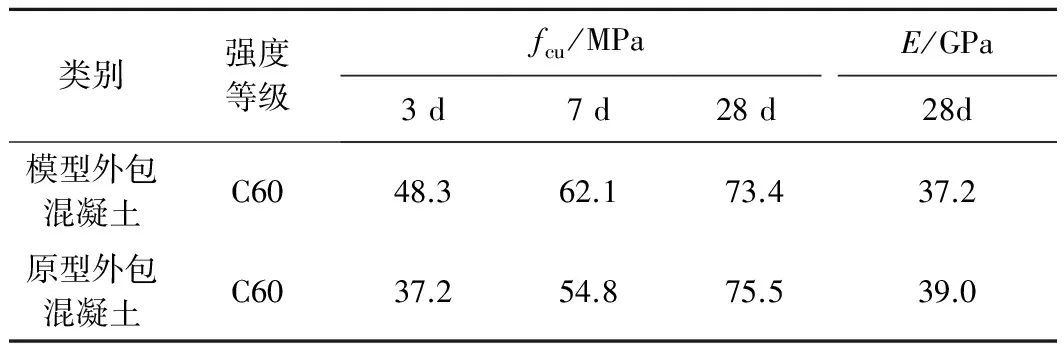
表4 C60外包混凝土材料性能试验结果

由表4可以看出，由于拱桥模型的骨料采用了粒径较小的细石，模型外包混凝土的28d立方体抗压强度和弹性模量分别为原型的97.2%和95.4%。

拱桥模型的主拱圈钢筋均与原型保持一致，其中拱圈分布筋和拱脚实心段钢筋采用φ8HPB235钢筋；拱圈横隔板和内侧腹板主筋均采用φ10HRB335钢筋；顶底板和外侧腹板的纵向主筋均采用φ12HRB335钢筋。

本次模型试验目的是模拟主拱圈的变形行为，前期的有限元模型分析表明，调整后的材料受力未达到其屈服强度，且拱桥模型和原型外包混凝土的强度及弹性模量较接近，因此本文试验方案对主拱圈变形的影响较小，拱桥模型可用来预测原型主拱圈的变形。

2.3 拱桥模型施工顺序及加载

为减小外界对拱桥模型的影响，模型试验选择在原型施工现场附近进行，模型施工共分为三步：架设主拱圈劲性骨架、灌注管内砂浆、浇筑外包混凝土。在进行原型外包混凝土施工时，除拱脚实心段混凝土外，剩余节段采取横向分环、纵向分段的方式逐步浇筑，施工过程复杂，技术难度大，工期长。模型试验在外包过程中进行适当简化，上下腹板合并后一次浇筑，外包混凝土的浇筑顺序如图8、图9所示。

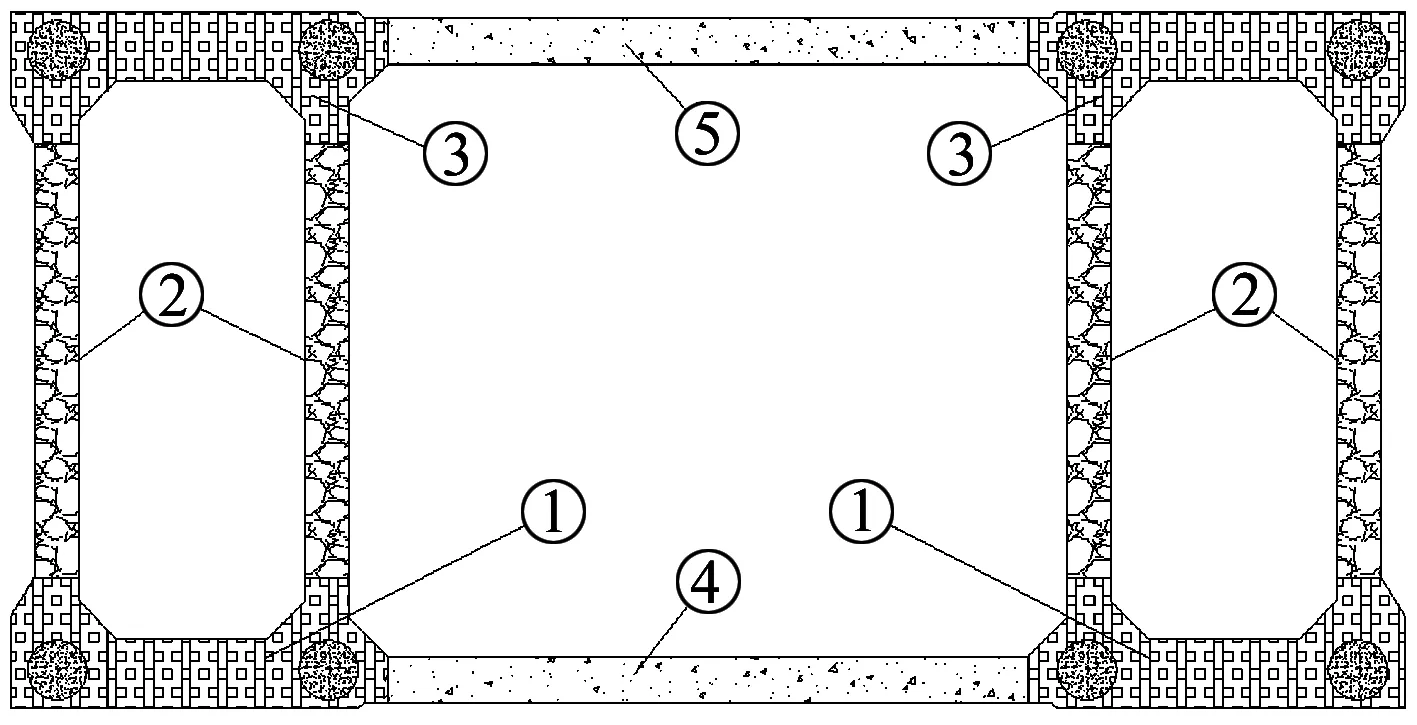
图8 拱顶段截面外包混凝土施工顺序

图9 拱脚段截面外包混凝土施工顺序

全桥模型共分为24个试验工况，对每个工况开始前后进行相关测试，文中只给出其主要施工工况和预测工况，见表5。

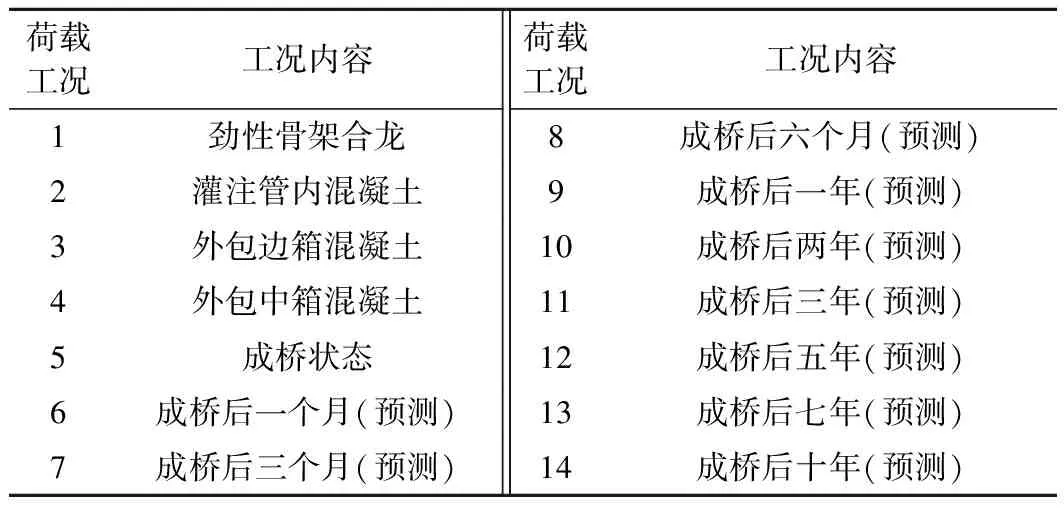
表5 主要施工工况和预测工况划分

为了补偿模型材料的容重，每次浇筑混凝土时需施加该混凝土自重6.5倍的荷载，由于施工现场操作空间有限、恒载补偿量较大，考虑到拱桥模型自重的受力特点，最终将模型主拱圈分为24段，每段设置2个恒载补偿节点，以分布集中力的形式进行恒载补偿。拱桥模型每部分的配重由其两侧的加载点按距离比例承担，配重块由素混凝土浇筑而成，平面尺寸均为2 m×1 m，每次加载时将相应配重块堆放在规格尺寸为2 m×1 m的加载平台上，每个加载点的补偿质量根据配重块的厚度确定(图5)。为了防止配重块脱落，需要保证加载梁始终处于水平状态，因此，在配重施加过程中，要不断调节加载梁前端与精轧螺纹钢拉杆连接处的锚固螺母，防止加载梁发生侧倾，恒载补偿节点的加载装置如图10所示。

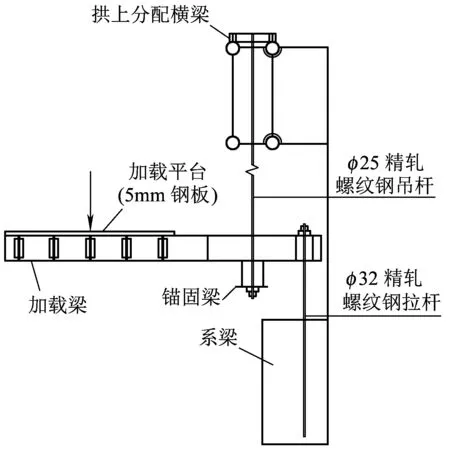
图10 加载点加载装置

2.4 测点布置

模型施工阶段需要对关键截面的竖向位移进行实时观测，模型主拱圈共布置7个位移测试截面，具体布置情况如图11所示。

各测试截面的测点横向布置如图12所示，W1和W2为位移测点。本文主要研究拱桥模型的变形，因此只关注拱桥模型主要控制截面的位移情况。

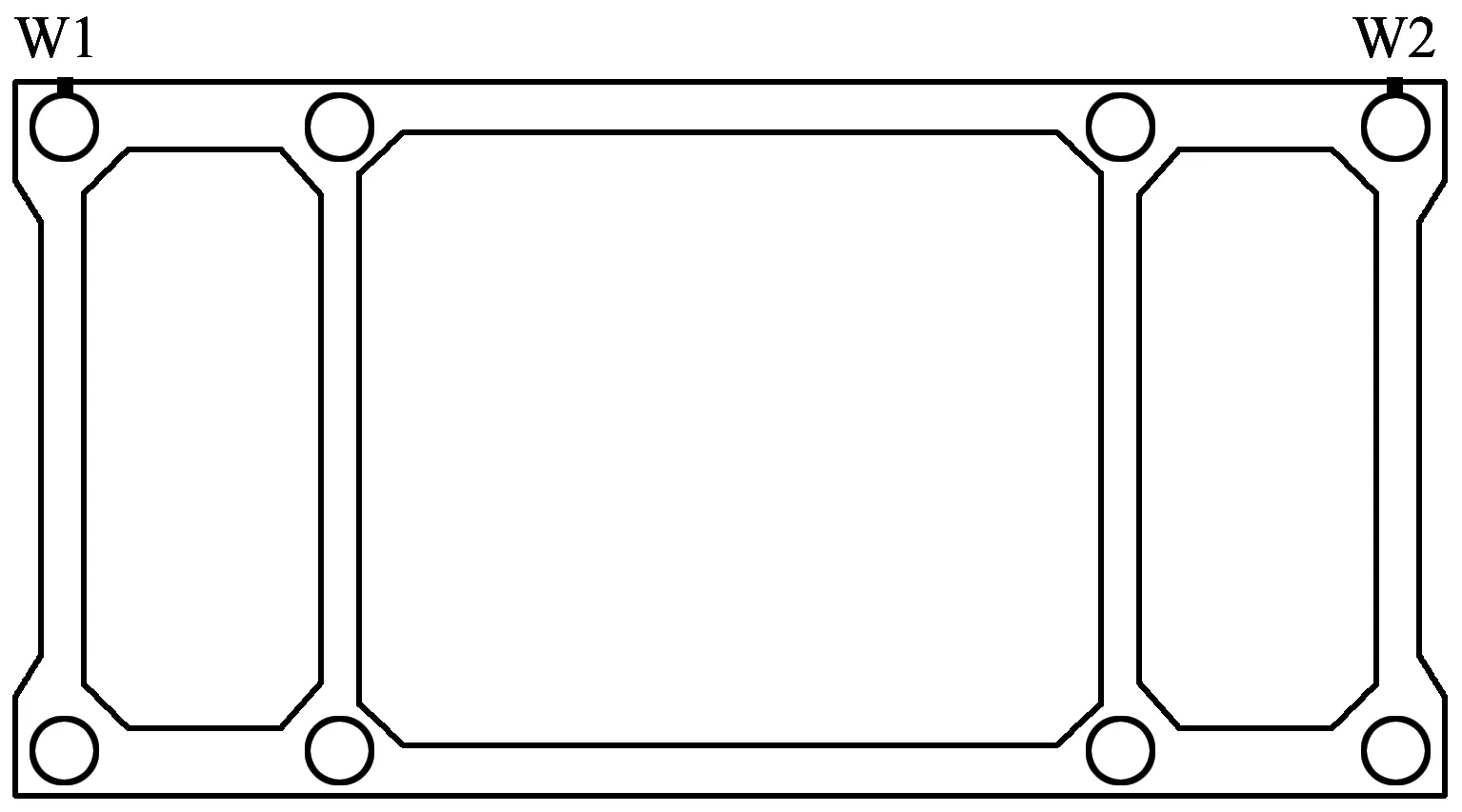
图12 位移测点布置图

3 大跨度钢筋混凝土拱桥收缩徐变计算模型

大跨度钢筋混凝土拱桥结构的变形将在混凝土收缩徐变特性的影响下持续发展，因此，合理选择混凝土收缩徐变计算模型，对准确预测钢筋混凝土拱桥的长期变形有重要意义。

文献[13]提出考虑环境湿度、体表比、加载龄期、干燥龄期和计算龄期等参数的GL2000模型。该模型可以较好预测高强混凝土的收缩徐变效应，并且考虑混凝土在加载前的干缩对加载后长期变形的影响。GL2000模型将荷载引起的长期变形表示为

(1)

式中：σ为试件加载应力；φ(t,τ)为混凝土徐变系数；Ec(τ)为加载龄期τ时混凝土弹性模量；Ec为混凝土28 d弹性模量。Ec计算表达式为

(2)

式中：fcm28为混凝土28 d轴心抗压强度平均值。

GL2000模型弹性模量随时间的发展方程为

(3)

(4)

式中：fcmτ表示混凝土加载龄期τ时混凝土轴心抗压强度平均值；Ⅰ型水泥：a=2.8，b=0.77；Ⅱ型水泥：a=3.4，b=0.72；Ⅲ型水泥：a=1.0，b=0.92。

徐变系数φ(t,τ)表达式为

(5)

当τ=tc时，φ(tc)=1；

当τ>tc时，

(6)

式中：φ(tc)为混凝土加载前即干燥时的修正系数；τ为混凝土构件的加载龄期，取7 d；t为混凝土构件的计算龄期，d，按照分析时的龄期取值；tc为混凝土潮湿养护结束时或开始干燥时的龄期，取3 d；RH为环境的相对湿度(用小数表示)，根据现场实测，外包混凝土取0.66，管内混凝土取0.96；V/S为混凝土构件的体表比，取50.8 mm。

GL2000模型收缩应变随时间发展的表达式为

εsh(t)=εshuβ(h)β(t)

(7)

(8)

β(h)=1-1.18RH4

(9)

(10)

式中：εsh(t)为混凝土构件计算龄期的收缩应变；εshu为收缩应变终值；β(h)为影响收缩的湿度修正；β(t)为影响收缩的时间修正；K为与水泥种类相关的系数[14]，取1；fcm28为混凝土28 d的轴心抗压强度平均值，根据实测，外包混凝土取50.7 MPa，管内混凝土取65.7 MPa。

4 建立有限元模型

4.1 建模思路

北盘江特大桥主拱圈采用横向分环、纵向分段逐步浇筑的施工方法，因此，施工顺序会导致混凝土龄期不同，同一截面上不同部位混凝土产生的收缩徐变效应也会有差异，使结构的长期变形更加复杂。如果直接采用一种单元模拟整个截面的力学行为则无法得到精确的计算结果。本文在建立北盘江特大桥有限元模型时，将同一截面上的外包混凝土、钢管和内填混凝土离散为相互平行的三个空间梁单元，前期计算结果表明，主拱圈结构具有较强的整体性，变形满足平截面假定，因此，采用“共节点”模拟同一截面上各单元的协同作用是可行的。由于收缩徐变分析的复杂性，且本文主要研究主拱圈的长期行为，所以在进行有限元模拟时，本次计算未考虑连接系、横隔板及拱上建筑的联合作用。

4.2 材料参数

模型中的各种材料按照原型结构中的材料特性定义，能够对模型试验中材料调整后的实测结果进行验证，并为后期预测长期变形提供支持。其中，钢管采用Q370，弹性模量2.1×105MPa，容重76.98 kN/m3；管内混凝土弹性模量取4.2×104MPa，容重26 kN/m3；外包混凝土弹性模量取3.9×104MPa，容重26 kN/m3；扣索弹性模量取1.95×105MPa，容重78.5 kN/m3。

4.3 边界条件及荷载

采用专业软件MIDAS/Civil建立拱桥模型有限元计算模型，用空间梁单元模拟管内混凝土、钢管和外包混凝土，用桁架单元模拟施工辅助扣索。根据设计，该桥主拱圈为无铰拱形式，所以在进行有限元模拟时，分别在两端拱脚处安装固定支座，将其全部自由度约束，在施工过程中不考虑扣索锚固端的偏移，也对锚固端的全部自由度进行约束。内填混凝土在浇筑初期，未达到设计强度时，只作为荷载作用于钢管上，此时按梁单元均布荷载模拟，待管内混凝土达到强度后考虑其刚度；外包混凝土的处理方法与管内混凝土相同，待外包混凝土的强度达到设计要求后，考虑其参与整体受力。在进行混凝土收缩徐变效应分析时，由于MIDAS/Civil中未自带GL2000模型，根据MIDAS/Civil的自定义功能，将GL2000模型嵌入到软件中。

4.4 施工阶段

根据设计，该桥主拱圈施工分析共设置269个施工阶段，拱上建筑施工设置12个施工阶段(文中模型不考虑此施工阶段)，成桥后的收缩徐变计算设置9个施工阶段，共计290个施工阶段。限于篇幅，不再对具体施工阶段加以介绍，主要施工阶段可参考表5。每个施工阶段激活或钝化相应的结构组、边界组和荷载组，并为各施工阶段新激活单元赋予其初始切向位移。主拱圈及施工节段有限元计算模型如图13、图14所示。

图13 主拱圈有限元计算模型

图14 施工节段有限元计算模型

5 收缩徐变对高速铁路钢筋混凝土拱桥时变行 为的影响研究

由于拱桥模型管内材料为CGM砂浆，其收缩徐变特性无法准确掌握，经计算，文中混凝土与原型中的C80混凝土存在较小差异，主拱圈的长期变形主要由外包混凝土控制，故在进行有限元分析时，管内材料仍按照C80混凝土分析。由于受到天气情况的影响，拱桥模型处环境湿度表现出较大的离散性，实测平均环境湿度为0.66，根据设计要求，水泥类型为快干普通水泥，考虑到管内混凝土处于封闭状态，与外界环境无水分交换，无收缩和干燥徐变，只考虑基本徐变，所以，令式(9)中的β(h)取0，求得管内湿度为0.96，外包混凝土收缩开始时间取为3 d。

5.1 模型计算与测试结果的对比分析

由于施工条件的限制，拱桥模型对实际施工过程做了适当简化，因此，针对拱桥模型施工过程中各主要荷载工况下控制截面的变形情况，将实测结果与有限元计算结果对比分析，如图15所示。

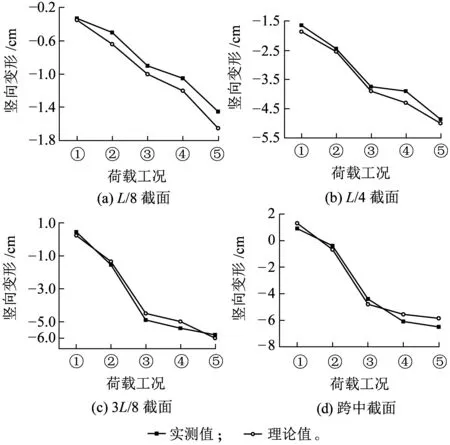
注：图中①～⑤代表荷载工况，依次为骨架合龙、内填混凝土、外包边箱、外包中箱和成桥状态。图15 拱桥模型施工过程主要控制截面竖向变形发展曲线

图15为拱桥模型自钢骨架合龙至成桥状态关键截面(图8、图9)的变形情况，其中包括结构自重和混凝土短期收缩徐变效应引起的变形，各截面的位移取该截面左右两个测点(W1和W2)的平均值。从图15可以看出，随着加载时间的增加，各主要截面的竖向变形呈增长趋势，其中理论值最大变形出现在拱顶截面附近，为5.7 cm。在施工过程中受到材料调整、施工过程简化等因素的影响，实测变形和理论变形之间产生较小的波动，最大波动值保持在1.0 cm以内。由于拱桥模型施工周期长，混凝土收缩徐变在短时间内就已经达到终值的75%左右，模型与原型外包混混凝土的弹性模量仅相差4.6%，因此对长期变形的预测结果不会产生较大影响。北盘江特大桥钢管混凝土劲性骨架截面占整个截面的比例较小，设计值为8.53%，且管内混凝土只考虑基本徐变，对主拱圈的变形影响较小，外包混凝土主要起控制作用，因此，拱桥模型的实测结果和有限元计算结果可以用来预测结构的长期变形。

根据上文的研究结果，对拱桥模型的长期变形进行预测。由于施工现场条件的限制，文中只给出拱桥模型一年内的变形实测数据，由有限元计算模型对其余时间工况的长期变形进行预测，如图16所示。

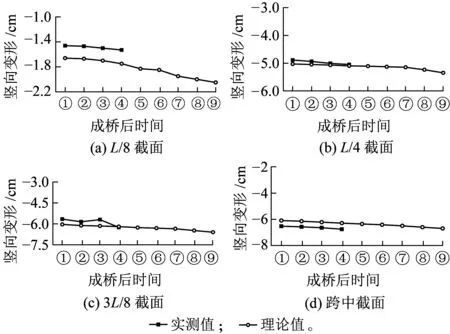
注：图中①～⑨代表成桥后时间，依次为成桥后1个月、3个月、6个月、1年、2年、3年、5年、7年和10年，图17、图19同。图16 收缩徐变效应对模型桥长期变形的影响分析

图16为模型桥在混凝土收缩徐变效应影响下的长期变形预测曲线，随着时间的推移，拱桥模型有持续下挠的趋势，在一年的观测周期内，其发展曲线出现较小波动。由于外界环境条件及人为因素的影响，在进行长期预测时，产生一定的误差，拱桥模型成桥后十年最大变形为6.7 cm，位于拱顶截面附近。

5.2 由拱桥模型计算结果反推原型变形分析

本节通过拱桥模型的预测结果反推原型变形情况，并将反推结果与原型确定性计算结果进行对比分析，原型确定性分析中的混凝土收缩徐变模型同样采用GL2000模型。为了提高模拟结果的准确性，二者采用相同的材料参数，根据拱桥模型设计时的相似原则，几何相似常数Cl=1/7.5，即拱桥模型的几何变形与原型成1∶7.5的比例关系。原则上，将拱桥模型的长期变形值按照7.5倍几何相似比进行放大，即得到原型的的长期变形量。拱桥模型反推结果与原型确定性分析对比如图17所示。由于拱桥模型主跨为59.33 m，其跨径与主跨445 m的原型相比存在较大差距，并且拱桥模型在试验过程中，受到了自然环境(如温度、湿度)等因素的综合影响。

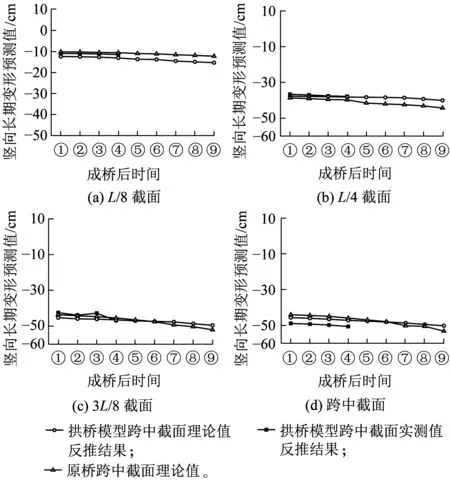
图17 拱桥模型反推结果与原型确定性分析结果对比

从图17可以看出，随着时间的推移，位移发展曲线表现出一定的波动，经计算，L/8截面两结果最大差值为1.8 cm，L/4截面两结果最大差值为2.5 cm，3L/8截面两结果最大差值为4.6 cm，跨中截面两结果最大差值为5.5 cm，最大误差控制在对应截面总位移的10%以内，因此，拱桥模型的整体变形是安全、合理的，其反推结果可为原型的施工及安全运营提供技术支持。

5.3 混凝土收缩徐变的随机性影响分析

北盘江特大桥是主跨445 m的特大型钢筋混凝土拱桥，其跨径以及外界环境条件与拱桥模型不同，混凝土的收缩徐变效应表现出较强的时变性和随机性。为了进一步得到具有概率保证意义的计算结果，需要考虑混凝土收缩徐变随机性对长期变形的影响[15]。

根据文献[10]的研究结果，徐变模型的随机性指徐变度函数J(t,τ)的随机性。考虑徐变和收缩模型的随机性，混凝土长期应变可以表示为

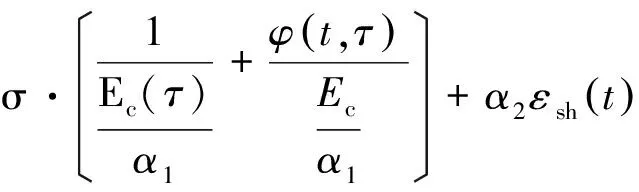
(11)

由式(11)可以看出，对徐变度离散性可以等效为对弹性模量的修改。由于加载龄期τ时的弹性模量和28 d时弹性模量都除以了一个相同的系数，所以不会影响到弹性模量的发展方程；对收缩的影响即为修改终极收缩系数，考虑到混凝土弹性模量、混凝土强度、环境湿度以及加载龄期等的随机性，混凝土的长期应变可以表示为

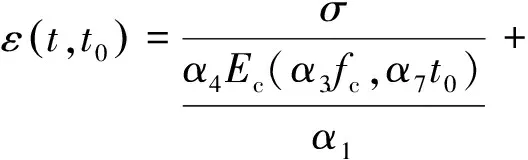
(12)

本节将考虑随机性的预测结果和反推结果(确定性分析结果)进行综合分析，得出更加符合实际变形的长期预测结果。为避免采用不同收缩徐变模型带来的计算误差，考虑随机性的混凝土收缩徐变模型同样基于GL2000模型，并采用拉丁超立方抽样技术(LHS)和基于响应面(RSM)的蒙特卡洛抽样技术(MC)，对原型的长期时变变形进行分析，GL2000模型随机因子(式(11)、式(12)中随机性系数)统计特性见表6。

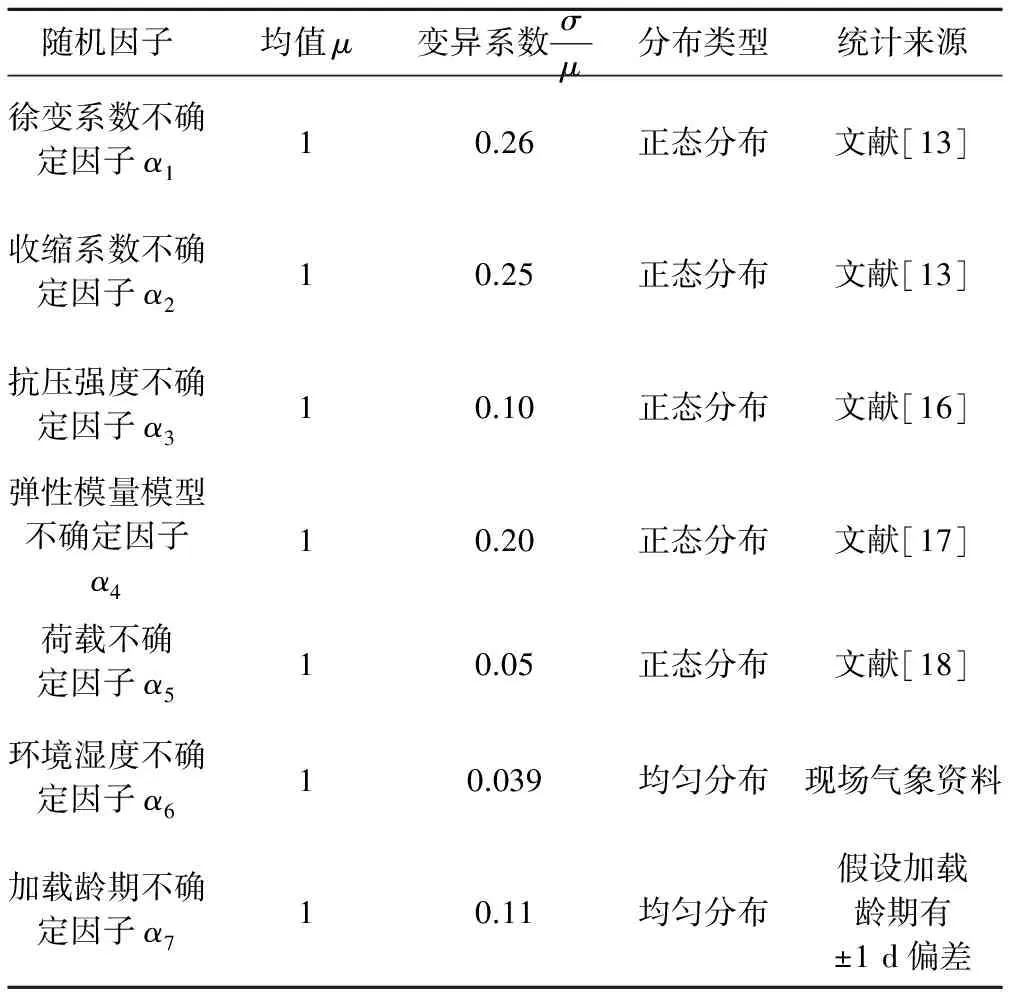
表6 GL2000模型随机因子统计特性

由上文研究结果可知，主拱圈变形的最不利截面位于跨中，故以跨中为代表截面进行分析。图18为原型跨中截面考虑混凝土收缩徐变随机性的MC结合RSM均值、98%分位值和2%分位值的预测结果。从图18可以看出，成桥后十年，拱顶截面确定性分析的相对位移增量为7.5 cm，随机性分析的跨中截面相对位移均值为8.1 cm，98%分位值为10.4 cm，是确定性分析结果的1.39倍，确定性分析得到的长期预测结果偏于不安全，因此，对大跨度混凝土拱桥进行收缩徐变分析时，考虑混凝土收缩徐变的不确定性是必要的。针对该桥成桥十年后跨中截面仍存在8.1 cm的位移增量，并且考虑到无砟轨道中扣件的标高调整量仅为2 cm，建议桥面铺设可调标高量较大的有砟轨道。

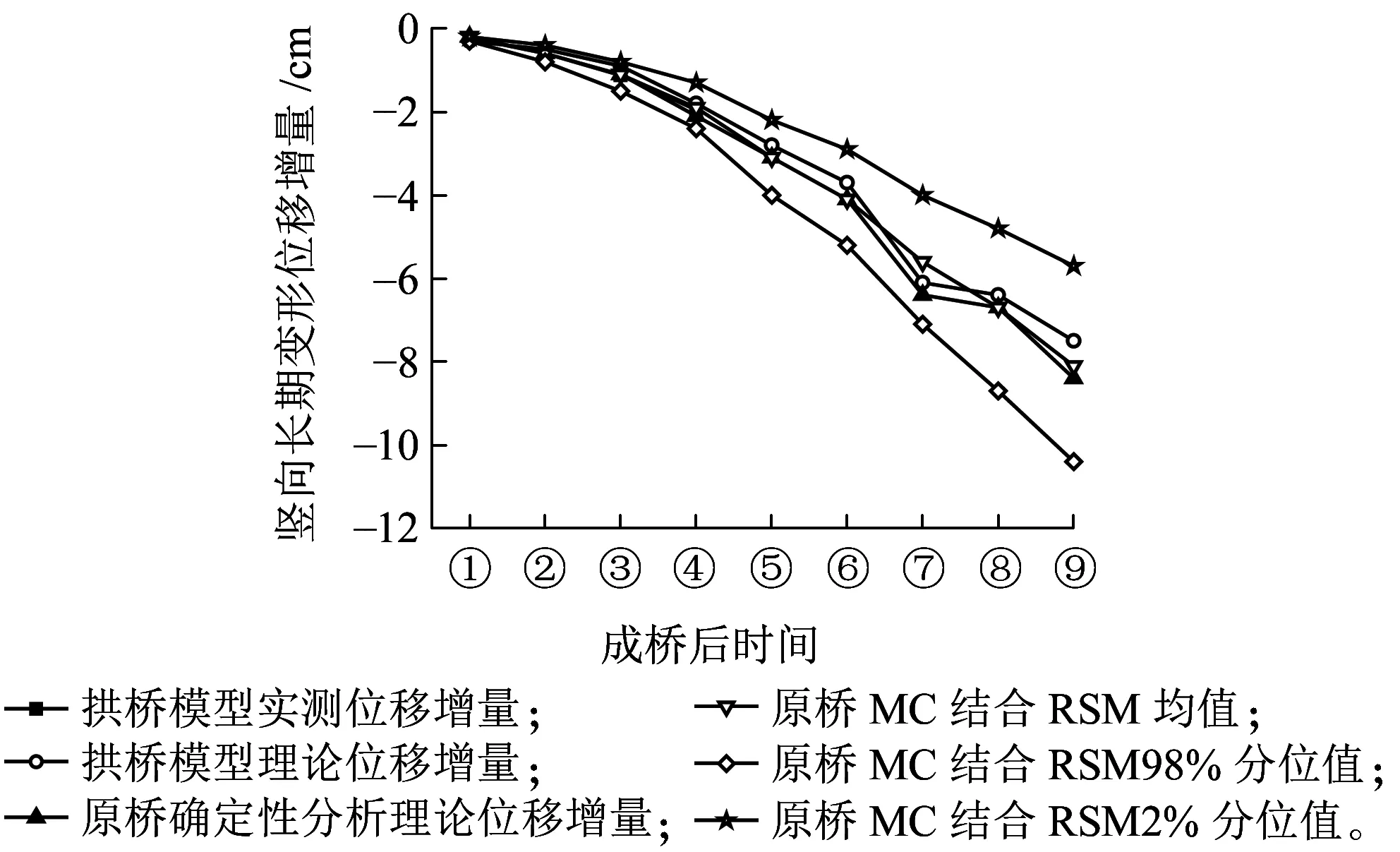
图18 拱桥模型与原型跨中截面长期变形增量综合对比结果

6 结论

以北盘江特大桥为工程背景，为验证原型施工过程的安全性并预测其长期变形，对主拱圈结构进行1∶7.5的大比例缩尺模型试验研究，得到以下结论：

(1)模型试验过程中，对外包混凝土的浇筑步骤进行简化；为了施工方便，对模型中的材料进行适当调整。通过对拱桥模型施工过程和成桥后时变行为的观测，得到实测值与理论值相差较小，整体力学性能良好，符合设计要求，验证了原型施工过程的安全性，并具有一定的安全储备。

(2)采用GL2000收缩徐变模型对主拱圈模型的长期变形进行预测，并根据几何相似比反推原型的长期变形。由于拱桥模型材料调整、施工工序简化和外界条件的影响，反推结果与理论计算结果没有严格遵守几何相似关系，呈现出一定的波动，最大差值为5.5 cm，误差控制在对应截面总位移的10%以内。

(3)将拱桥模型和原型的确定性分析结果与原型考虑混凝土收缩徐变随机性的结果进行对比分析，确定性分析结果与随机性分析结果表现出一定的差异。成桥后十年，随机分析结果的98%分位值是确定性分析的1.39倍，是随机分析均值的1.3倍，因此，对于收缩徐变较敏感的大跨度桥梁结构，确定性分析的预测结果偏于不安全，需要考虑收缩徐变的随机性影响。

(4)随机性分析得到的概率性结果建立在大量样本统计的基础上，并针对样本的离散性预判各种响应值出现的范围。为了更准确预测主拱结构的长期变形，建议开展主拱圈混凝土收缩徐变、强度和弹性模量的材料试验，并对桥址处环境温、湿度进行实时监测，用以修正模型，提高预测精度。同时加强控制全桥施工质量，关注主要截面的变形情况；针对桥面的残余收缩徐变变形，如果铺设无砟轨道，其扣件的一般调整量仅为2 cm，因此，建议铺设可调标高量较大的有砟轨道，为高速铁路的安全运营提供条件。

参考文献：

[1]顾安邦，刘忠，周水兴.万县长江大桥混凝土时效和几何、材料等非线性因素影响分析[J].重庆交通学院学报，1999，18(4)：1-7.

GU Anbang，LIU Zhong，ZHOU Shuixing. Analysis of Time Dependent Effects of Concrete and Geometrical Nonlinearities，Material Nonlinearities of Wanxian Yangtze Ri-ver Bridge[J]. Journal of Chongqing Jiaotong Institute，1999，18(4)：1-7.

[2]郑皆连.特大跨径RC拱桥悬拼合拢技术的探讨[J].中国公路学报，1999，12(1)：41-48.

ZHENG Jielian. Discussion on Technology of Suspending and Connecting for the RC Bridge with an Unusual Big Span[J]. China Journal of Highway and Transport，1999，12(1)：41-48.

[3]汤小波，谢冀萍，赵世春，等.万县长江大桥钢筋混凝土拱模型试验研究[J].西南交通大学学报，1994，29(4)：362-367.

TANG Xiaobo, XIE Jiping, ZHAO Shichun, et al. Experimental Research of Model RC Arch for Wanxian Yang-tze River Bridge[J]. Journal of Southwest Jiaotong University，1994，29(4)：362-367.

[4]李晓斌，杨永清，蒲黔辉，等.钢筋混凝土拱桥悬臂浇筑施工模型试验研究[J].西南交通大学学报，2007，42(5)：526-530.

LI Xiaobin，YANG Yongqing，PU Qianhui，et al. Model Test of Cantilever Casting Construction of Reinforced Concrete Arch Bridge[J]. Journal of Southwest Jiaotong University，2007，42(5)：526-530.

[5]崔军，孙炳楠，楼文娟，等. 钢管混凝土桁架拱桥模型试验研究[J].工程力学，2004，21(5)：83-86.

CUI Jun，SUN Bingnan，LOU Wenjuan， et al. Model Test Study on Concrete Filled Steel-tube Truss Arch Bridge[J]. Engineering Mechanics，2004，21(5)：83-86.

[6]李乔，田学民，张清华.铁路大跨度提篮式系杆拱桥全桥模型试验[J].中国铁道科学，2003，24(1)：88-92.

LI Qiao，TIAN Xuemin，ZHANG Qinghua. A Model Test on Long-span X-style Tied Arch Bridge on Railway[J]. China Railway Science，2003，24(1)：88-92.

[7]刘爱荣，张俊平，赵新生，等.中山一桥模型试验及理论分析[J]. 中国公路学报，2005，18(3):75-79.

LIU Airong，ZHANG Junping，ZHAO Xinsheng，et al. Model Test of the First Zhongshan Bridge and Theoretical Analysis[J]. China Journal of Highway and Transport，2005，18(3)：75-79.

[8]范亮，龚尚龙，陈思甜.特大跨径钢桁拱桥施工过程模型试验[J].西南交通大学学报，2010，45(4)：502-507.

FAN Liang，GONG Shanglong，CHEN Sitian. Model Experiment of Construction Process of Long-span Steel Truss Bridge[J]. Journal of Southwest Jiaotong University，2010，45(4)：502-507.

[9]胡志坚，张明辉，孔祥韶，等.大跨度钢桁架拱桥静动力相似模型[J].中国公路学报，2014，27(9)：82-89.

HU Zhijian，ZHANG Minghui，KONG Xiangshao，et al. Static and Dynamic Experimental Model for Long-span Steel-truss Arch Bridge[J]. China Journal of Highway and Transport，2014，27(9)：82-89.

[10]BAZANT Z P. Random Cree Pand Shrinkage in Structures：Ampling[J]. Journal of Structural Engineering，ASCE，1985，111(5)：1 113-1 134.

[11]GOEL R，KUMAR R，PAUL D K. Comparative Study of Various Cree Pand Shrinkage Prediction Models for Concrete[J]. Journal of Materials in Civil Engineering，ASCE，2007，19(3)：249-260.

[12]BAZANT Z P，LI G H. Unbiased Statistical Comparison of Cree Pand Shrinkage Prediction Models[J]. ACI Materials Journal，2008，106(6)：610-621.

[13]GARDNER N J. Comparison of Prediction Provisions for Drying Shrinkage and Cree Pof Normal-strength Concretes[J]. Canadian Journal of Civil Engineering，2004，31(5)：767-775.

[14]GARDNER N J，LOCKMAN M J. Design Provisions for Drying Shrinkage and Cree Pof Normal-strength Concrete[J]. ACI Materials Journal，2001，98(2)：159-167.

[15]BAZANT Z P. Prediction of Concrete Cree Pand Shrinkage：Past，Present and Future[J]. Nuclear Engineering and Design，2001，203(1)：27-38.

[16]CEB-FIP Model code 1990[S]. London：Thomas Telford House，1993.

[17]PASCAL L. Reliability-based Deterioration Model for Deflection Limit State in Steel Girder Bridges[D]. Michigan：University of Michigan，2006.

[18]国家质量技术监督局， 中华人民共和国建设部. GB/T 50283—1999公路工程结构可靠度设计统一标准[S].北京：中国计划出版社，1999.