通用楔形管片盾构隧道曲线段线路拟合算法及应用
2016-05-08吴海彬晏启祥程天健
吴海彬,何 川,晏启祥,封 坤,程天健
(西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031)
目前,通用楔形管片在输水管线、城市地铁以及大断面水下盾构隧道中广泛应用[1-3]。盾构隧道一般埋深较浅,常需要以小半径曲线绕避浅层地基基础和地下管线等障碍[4,5]。目前,盾构隧道一般采用普通衬砌环和通用管片环两种管片环形式模拟曲线线形[6]。普通衬砌环以左转弯环、右转弯环和直线环拟合曲线线路,同时为满足曲线拟合和施工纠偏的要求,经常需要对转弯环进行特殊设计加工[7]。由于转弯环的拼装点位固定,对隧道轴线的精确控制较为不利[8,9]。通用管片环依靠预先设定的楔形量,通过改变邻近管片环的旋转角度,不断调整隧道中线以使其尽可能逼近线路中线。由于通用性强、拼装效率高、线路控制精准且易于纠偏等优点,通用楔形管片越来越多地运用于城市地铁和大断面水下盾构隧道的建设中。
目前,国内外相关研究主要集中在盾构隧道通用楔形管片的排版与选型研究上[10,11],虽然其中涉及到部分曲线段的拟合问题,但均未详述通用楔形管片盾构隧道曲线拟合的原理和算法,并且对于将该算法运用于解决管片参数能够拟合的最小曲线半径、不同管片参数对曲线拟合精度的影响、管片初始偏位和偏向对纠偏工作的影响等关键问题上,目前缺少相关研究工作。因此,本文基于盾构隧道曲线拟合原理和算法,对最小曲线半径的确定、拟合曲线精度的评价以及管片环初始拼装误差的影响等问题进行研究。
1 盾构隧道曲线拟合原理与关键算法
在盾构隧道曲线段线路拟合时,实际管片环以多段折线逼近设计的光滑曲线线路,如图1所示。其原理可概括为:当第i环管片完成拼装后,第(i+1)环管片在与第i环管片密贴的基础上,沿第i环管片前进面外法向Vni进行旋转。旋转不同角度所得到的第(i+1)环管片前进面中心点Ai+1分布于以第i环管片前进面中心点Ai为顶点、顶角为θ、对称轴为Vni的锥面上,通过比较锥面上Ai+1的可能位置以及Ai+1对应的理论点位Bi+1确定第(i+1)环管片的拼装位置。如此往复,最终完成对整条曲线线路的拟合,其关键算法如下:
(1)确定第i环管片的关键点与关键向量
当第i管片环完成拼装之后,该管片环前进面的中心点坐标Ai(x,y,z)、前进面上封顶块外弧长中点坐标Fi(x,y,z)、前进面上标准幅宽处特征点坐标Wi(x,y,z)即可确定。其中Wi(x,y,z)位于管片外表面上,并由AiWi、AiFi和管片环轴向向量Vai构成正交系。
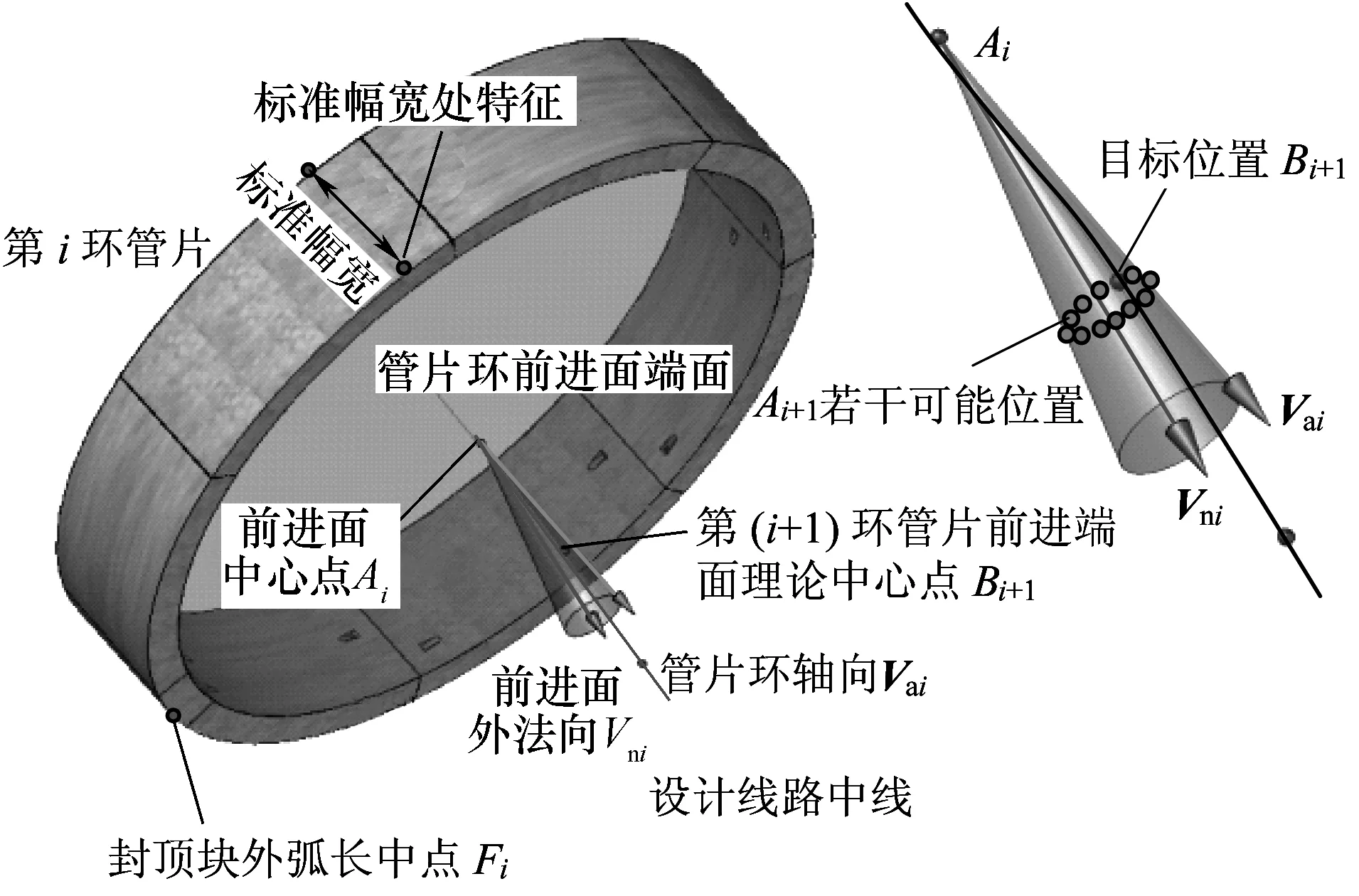
图1 通用楔形管片盾构隧道曲线拟合原理
管片环轴向向量Vai由前后环前进面中心点按式(1)计算确定,管片前进面法向向量Vni由前进面两相互垂直的单位向量n1、n2确定,分别由式(2)~式(4)计算确定。
(1)
(2)
(3)
(4)
(2)计算第(i+1)环管片前进端面的理论中心点Bi+1(x,y,z)
由二分法计算Bi+1(x,y,z),其过程为:假定设计线路上各点坐标为函数f(x,y,z),选取Ai(x,y,z)为近点f0(x,y,z),选取曲线末端为远点f1(x,y,z),试算点即为近点与远点的中点fm(x,y,z),计算fm(x,y,z)与Ai(x,y,z)的距离,若距离大于管片幅宽d,以试算点作为新的远点f1(x,y,z)进行计算;若距离小于d,以试算点作为新的近点f0(x,y,z)进行计算,继续迭代直至得到与Ai相距为d的试算点,即为前进端面的理论中心点Bi+1。
(3)确保相邻环管片密贴
第(i+1)环管片由第i环管片位置出发,沿该管片环轴向Vai平移距离d,此时生成的第(i+1)环管片与第i环管片有部分相互嵌入,部分相互分离。为消除侵入和空隙,将此时第(i+1)环管片绕管片环轴向Vai旋转180°,使两环管片楔形量相互填补,达到环间密贴要求,其过程如图2所示。
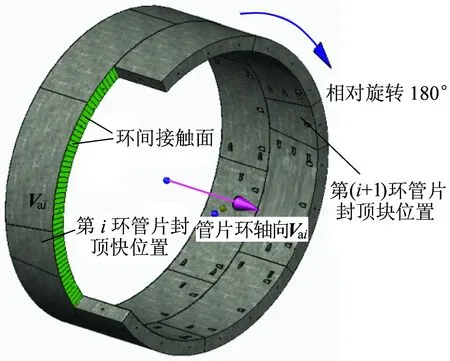
图2 相邻管片环环间密贴过程

(5)
同样,管片的旋转表现为关键点位的旋转。空间点位P(x,y,z)绕过原点的向量r=[a1a2a3]旋转θ角,旋转后的P′(x′,y′,z′)为[12]
(6)
(4)试算拼装位置
为确保初始时刻相邻两环管片纵向螺栓对齐,需要在相邻两环管片密贴的基础上,将第(i+1)管片环绕Vni旋转180°,管片环上各点旋转后的位置通过式(6)计算获得。同时根据设计的管片拼装方式确定相邻管片环允许的拼装角度。若管片环间纵向螺栓为N颗等间距分布,当设计拼装方式允许通缝拼装时,将第(i+1)环管片绕Vni旋转(360k/N)°(k=0,1,2,3,…,N-1),得到该环管片N个可能的拼装位置,相应的关键点A‴i+1,k通过式(6)计算。各试算位置管片的环拼装误差εk由式(7)、式(8)得到,εmin对应的拼装角度即为最佳拼装角度。将关键点旋转最佳拼装角度,确定第(i+1)环最终的关键点Ai+1、Fi+1、Wi+1。
εk=‖A‴i+1,k(x,y,z)-Bi+1(x,y,z)‖
(7)
εmin=min{ε1,ε2,ε3,…,εN}
(8)
若拼装方式为错缝拼装,在通缝拼装的基础上仍需剔除导致通缝的可能拼装位置。如:狮子洋盾构隧道,管片采用“5+3+1”的分块形式,纵向螺栓为22颗等间距分布,采用1/3错缝拼装方式,则两环管片的相对转角只可能为2、5、8、11、14、17、20倍螺栓间夹角。因此A‴i+1,k只能绕Vni旋转(360k/N)°(k=2,5,8,11,14,17,20),并且通过式(7)、式(8)计算εmin,最终下一环管片的拼装位置如图3所示。
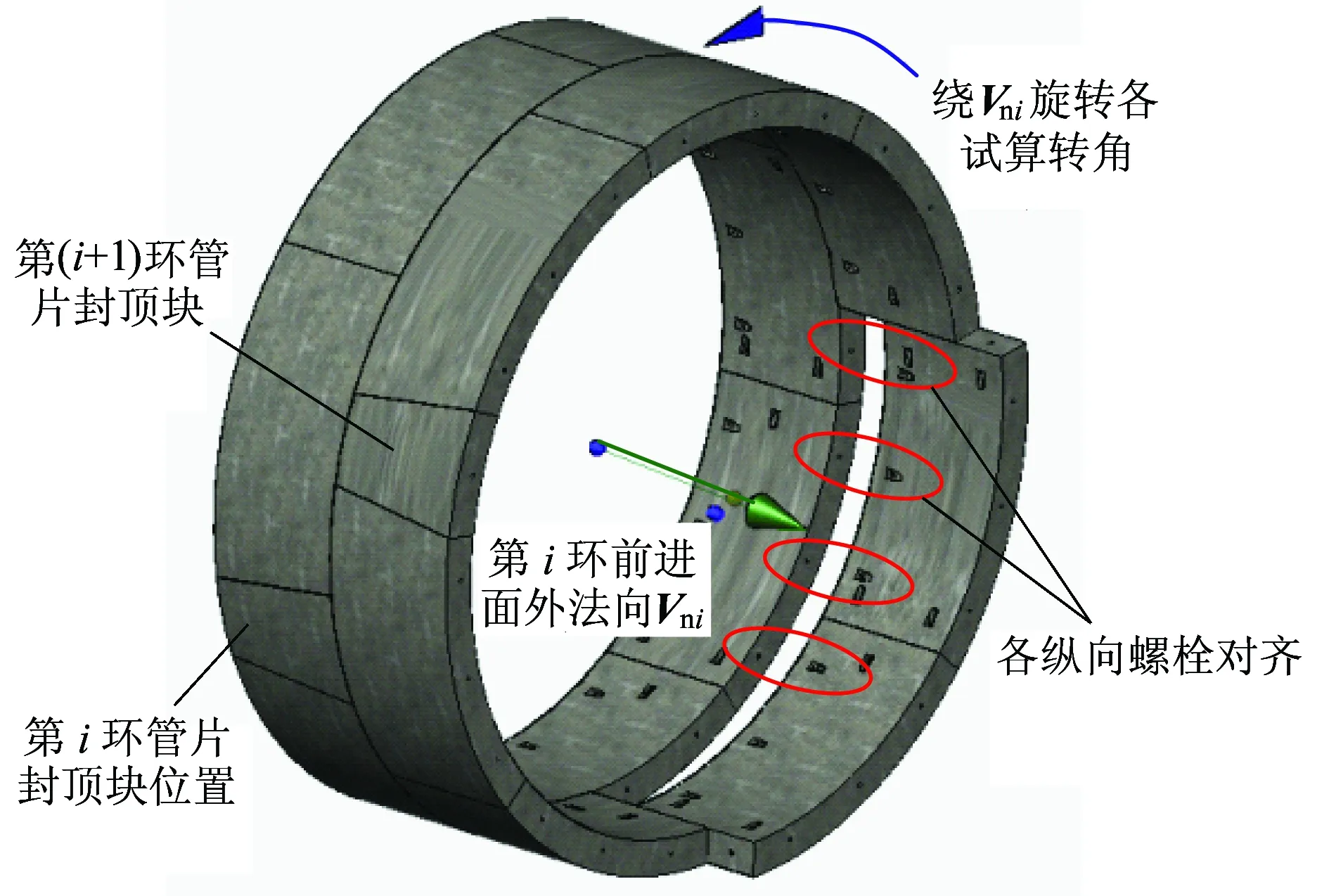
图3 目标环合理拼装点位试算过程
(5)循环直至完成对整段线路的拟合
由第(i+1)环的关键点Ai+1、Fi+1、Wi+1,通过上述过程(1)~(4),计算第(i+2)环的各个关键点位Ai+2、Fi+2、Wi+2,确定第(i+2)环管片的最终拼装位置,以此类推,直至完成对整段曲线线路的拟合。
2 不同管片参数能拟合的最小曲线半径
目前,相关规范对盾构隧道最小曲线半径没有针对性的条款,过于笼统。如《水工隧洞设计规范》提出转弯半径不宜小于5.0倍洞径,最低可放宽到3.0倍洞径。而地铁盾构隧道虽然提出正线、联络线、车场线等的最小曲线半径,但缺乏对特殊工况的考虑,如目前地铁盾构隧道的管片外径通常在6.0 m左右,而南京地铁盾构隧道采用单洞双线设计,外径达到11.8 m,此时相应的最小曲线半径是否适用尚无定论。对于目前在城际客运专线上大范围使用的大断面盾构隧道,其管片环所能拟合的曲线半径也缺少相关的规范规定。因此,针对不同的管片外径、楔形量、幅宽等参数,研究其能拟合的最小曲线半径在线路设计、管片选型等问题上有实际意义。
2.1 最小曲线半径的判别标准
在盾构管片外径、楔形量、管片幅宽、管片拼装方式等条件确定时,为寻找对应的最小曲线半径,需要建立相应的判定标准。GB 50446—2008《盾构法隧道施工与验收规范》规定了管片拼装过程中,隧道轴线在高程和平面允许的偏差,见表1。

表1 盾构隧道管片环拼装允许偏差 mm
为此,对任意曲线半径R,选定足够多的管片环数n对其进行拟合,建立该管片环参数对该曲线半径能否拟合的判别标准:
(1)max{E1,E2,E3,…,En}不大于规范允许误差;
(2){E1,E2,E3,…,En}无明显发散规律。
其中,Ei表示第i环管片的拼装误差,条件(1)表示拟合的隧道线路与设计线路在平面以及高程上满足最大拼装误差Emax不大于规范允许误差;条件(2)表示各环管片的拼装误差序列{E}无发散规律。若符合上述条件,则认为该类型管片环满足该半径曲线的线路拟合要求,若有其一不满足,则认为该类型管片环无法对该半径曲线进行拟合,管片环所能拟合的最小曲线半径判别标准如图4所示。
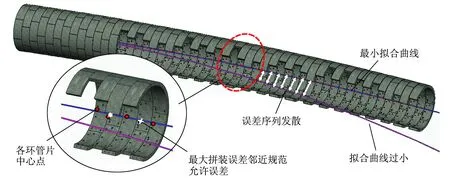
图4 管片环所能拟合的最小曲线半径的判别标准示意
设定试算半径上下限Rup、Rdown,其中Rup应足够大,确保以上判定准则下管片环能对其进行拟合;同时,Rdown应足够小,使该类型管片环无法对其进行拟合。取Rm=(Rup+Rdown)/2试算,若满足以上判定准则,以Rm更新Rup进行下一步试算;反之以Rm更新Rdown进行下一步试算。通过二分法,不断缩小试算的曲线半径范围,最终确定的临界曲线半径即为该管片参数能拟合的最小曲线半径。如:外径6.0 m、幅宽1.5 m、楔形量36 mm的管片参数条件下,最小曲线半径试算范围的缩减过程如图5所示。

图5 最小曲线半径的求解过程示意
2.2 典型参数范围内最小曲线半径与管片参数的相关性分析
本文针对不同的小断面水工盾构隧道、中等断面城市地铁盾构隧道以及大断面城际铁路盾构隧道的典型管片参数,以通用楔形管片盾构隧道曲线拟合原理为基础,依据上述最小曲线半径的判别标准,得出典型管片参数下的最小曲线半径,见表2。
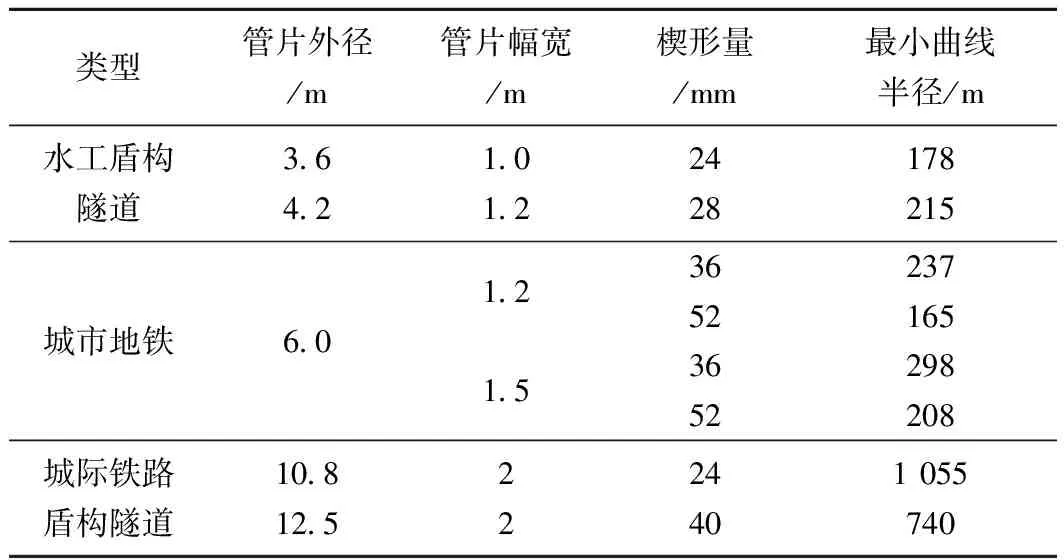
表2 管片典型参数所能拟合的最小曲线半径
由于实际工程问题涉及的管片尺寸各异,无法对各种尺寸的管片环所能拟合的最小曲线半径一一枚举。因此,需要进行典型参数范围内最小曲线半径与管片参数的相关性研究,掌握最小曲线半径随各几何参数变化的一般规律,并在典型参数确定的最小曲线半径基础上,对现有管片环参数要拟合的曲线半径进行对比论证。
因此,本文以楔形量24 mm、管片外径4~16 m、管片幅宽1.0~2.0 m的典型值,研究管片外径、幅宽与所能拟合的最小曲线半径的变化规律,如图6所示。
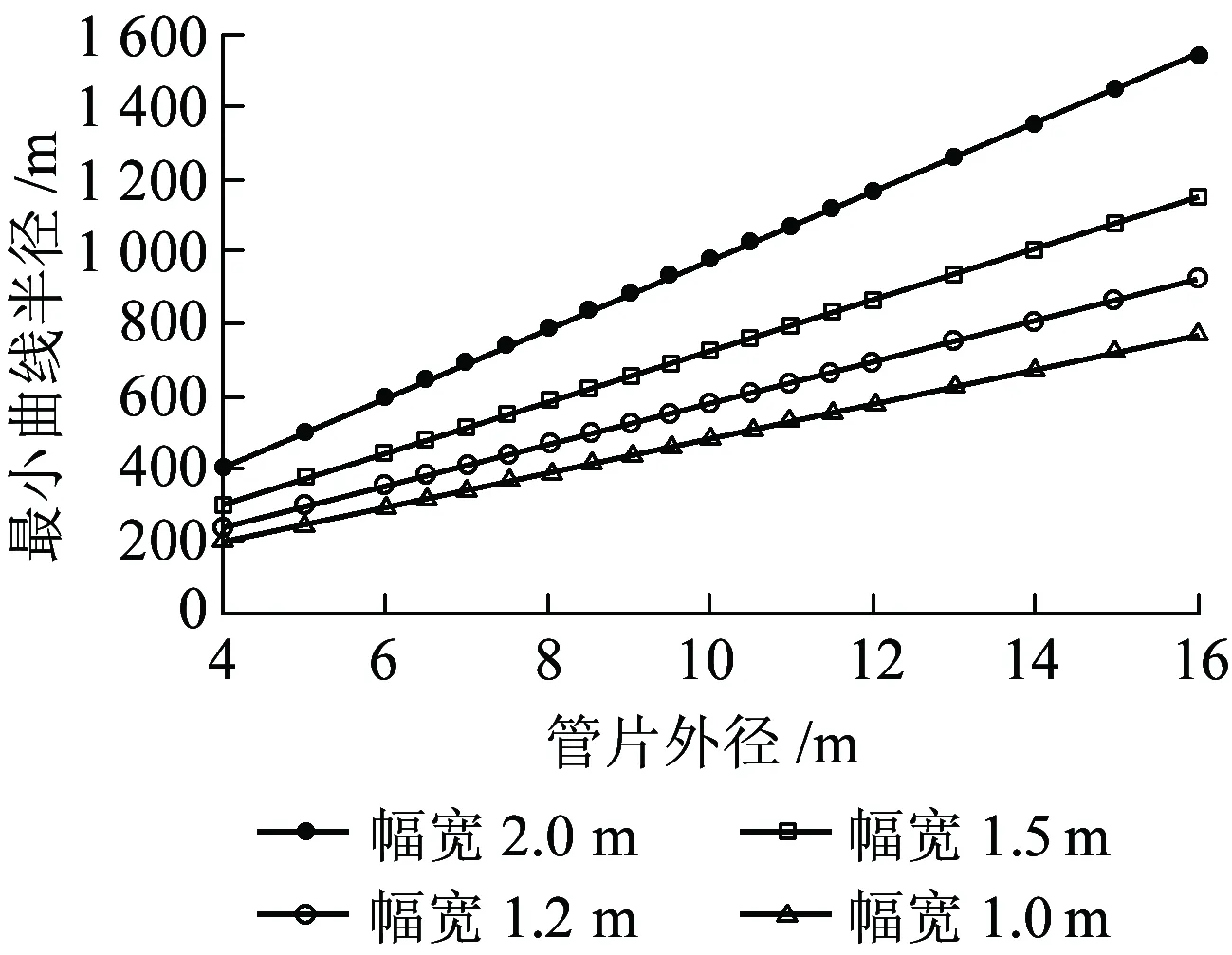
图6 外径、幅宽与最小曲线半径对应关系
从图6可以看出,在管片环幅宽和楔形量确定时,管片外径与所能拟合的最小曲线半径大致正相关,随着管片外径的增大,所能拟合的最小曲线半径线性增长,管片幅宽越大增长越剧烈。同时,管片幅宽越小,在外径和楔形量确定的情况下管片环所能拟合的最小曲线半径越小。
以幅宽2.0 m,管片外径4~16 m、管片楔形量16~52 mm为例,研究管片楔形量、外径与管片环所能拟合的最小曲线半径的对应关系,如图7所示。
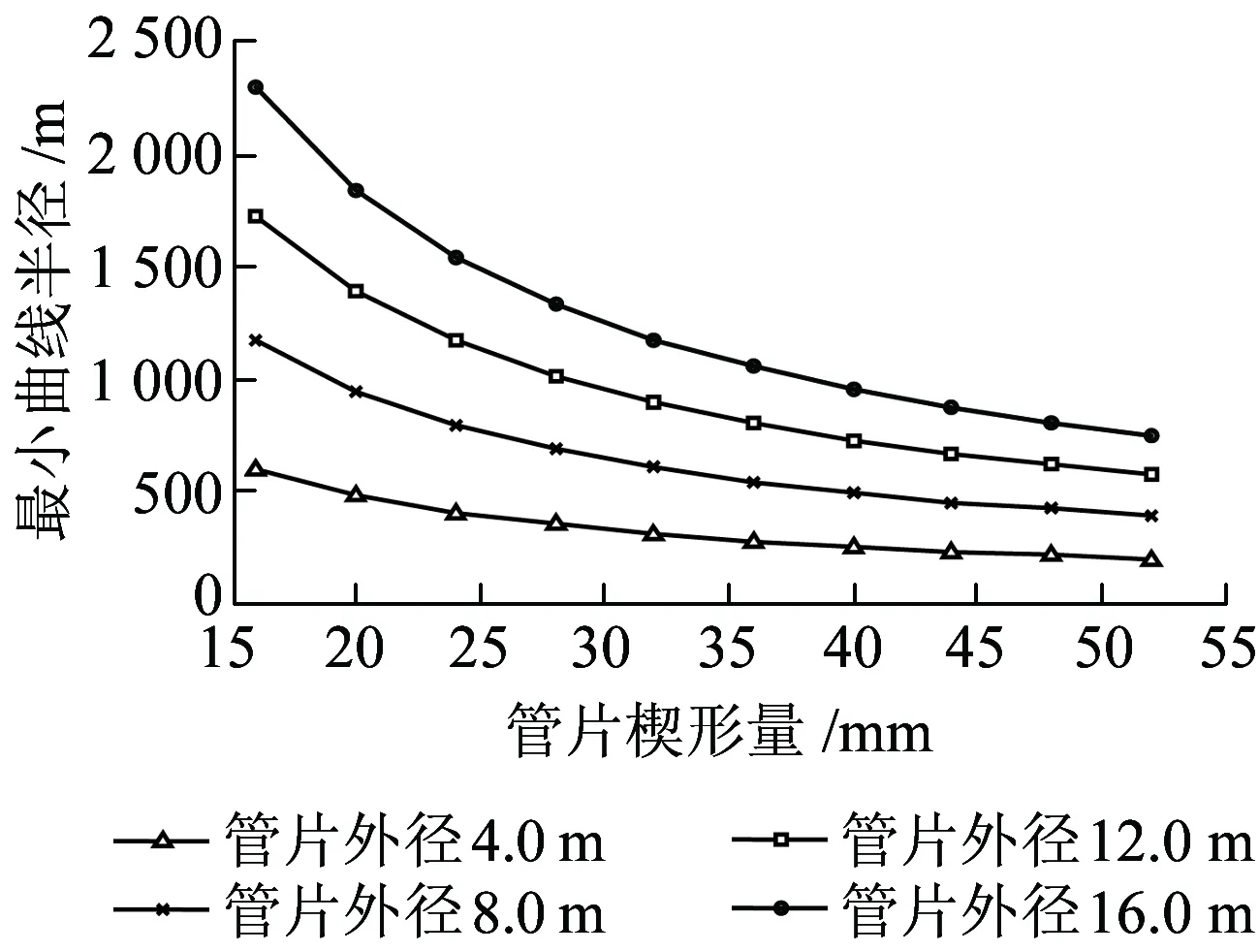
图7 楔形量、外径与最小曲线半径对应关系
从图7可以看出,在管片外径和幅宽确定时,最小曲线半径随楔形量的增加有减小的趋势,这种趋势随管片楔形量的增加变得不明显,同时管片外径越小,最小曲线半径随楔形量的增加减小得越缓慢。
3 不同管片参数与曲线拟合精度的相关性分析
盾构隧道曲线段拟合时,即便管片参数满足对设计曲线线路的拟合要求,若隧道中线偏离设计轴线过多,也会造成线路不平顺,严重时还将制约行车速度,影响旅客乘车舒适性。因此,在管片环满足设计曲线线路拟合的条件下,研究不同管片参数与曲线拟合精度的相关性对优化管片设计、提高曲线线路拟合质量有重要意义。
3.1 曲线拟合精度的评价
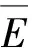
Emax=max(E1,E2,E3,…,En)
(9)
(10)
(11)
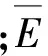
3.2 不同管片参数与曲线拟合精度的相关性分析
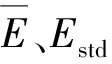
由列车行车限界和建筑限界可以确定盾构管片环外径为6.0 m,根据不同管片参数所能拟合的最小曲线半径分析方法可得:为拟合该曲线要求管片幅宽小于2.0 m,管片环楔形量大于20 mm。鉴于常见楔形量最大值可取52 mm,取中间值36 mm的楔形量分析幅宽与理论上空间最大拼装误差的对应关系,如图8所示。
从图8可以看出:拟合小半径曲线时,随着管片环幅宽的减小,空间最大拼装误差整体上有减小趋势。但当幅宽小于1.2 m时,减小管片幅宽对降低管片拼装误差影响较小。同时管片幅宽过小,同等里程内管片环间接缝相应增多,增加了渗漏水环节,并且制约施工进度。以1.2 m的幅宽分析楔形量与理论上空间最大拼装误差的对应关系,如图9所示。
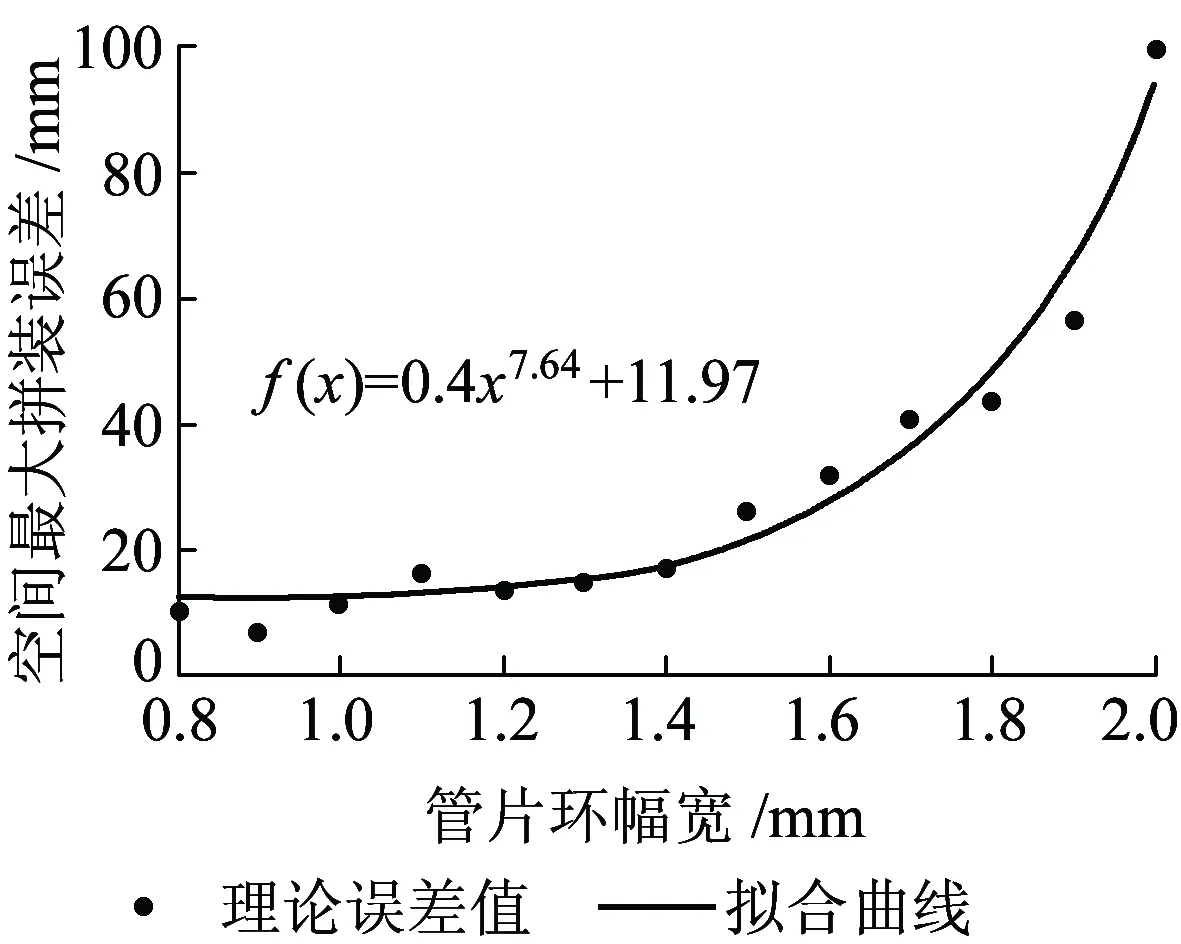
图8 空间最大拼装误差随幅宽变化规律

图9 空间最大拼装误差随楔形量变化规律
从图9可以看出:在一定范围内(楔形量20~26 mm),空间最大拼装误差随管片环楔形量的降低快速减小,超过该范围(大于26 mm)楔形量的继续减小对降低理论拼装误差作用有限。由于楔形量的增大不会对管片环质量和整体尺寸有大的改变,因此为提高曲线拟合精度,楔形量可取较大值。
根据分析结果,筛选4组不同管片参数方案,计算不同方案下该曲线段的拟合精度,见表3。通过计算比较不同方案中盾构隧道曲线拟合的空间最大偏差、水平和竖向误差均值、水平和竖向误差均方差,可以看出方案2,即幅宽1.2 m、楔形量38 mm拟合该曲线有较高的精度。

表3 不同方案各曲线拟合精度评价指标
4 管片环初始拼装偏差对后续曲线拟合精度的影响
管片环的拼装误差表现为两个方面,即:管片环关键点位置偏离设计位置,管片环轴线方向偏离设计轴线切向。若管片环初始拼装误差过大,可能造成后续管片环无法通过调整设计的排版达到曲线拟合精度要求。因此,本文结合某地铁盾构区间管片参数(幅宽1.2 m,管片外径6 m,楔形量38 mm),依据通用楔形管片盾构隧道曲线拟合原理,分析管片环初始拼装误差对曲线拟合精度的影响,以及初始管片拼装误差的允许范围。
4.1 管片环偏位对曲线拟合的影响
盾构隧道曲线拟合时,管片环偏位是指管片环位置的控制点偏离设计点位,管片环的轴向与设计曲线上控制点的切向一致,如图10所示。

图10 管片环关键点偏位示意
以管片环前进面中点为控制点,研究管片环水平初始偏位对管片环拟合精度的影响。取初始水平偏位误差为30 mm,分别考虑初始误差位于曲线内外侧两种情况下,后续50环管片各自的拼装误差,如图11所示。
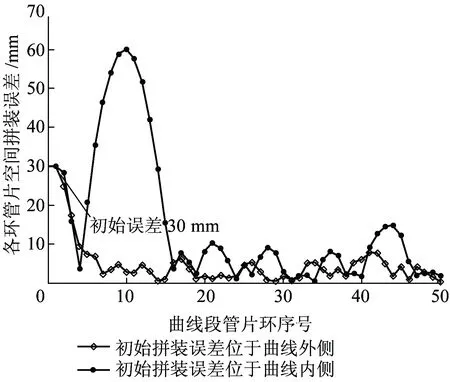
图11 曲线内外侧管片环初始偏位下后续管片环的拼装误差
从图11可以看出:相比于管片环的初始内向偏位,外向偏位对管片的纠偏较为有利,在外向偏位的影响下管片的拼装误差更容易达到要求。其原因为:初始偏位偏离曲线之外相当于相同管片尺寸条件下拟合较大半径的曲线,拟合效果更佳;当初始偏位偏离曲线之内时,为使最初几环管片中心点尽快回归设计轴线,管片环的轴线会过度偏离设计轴线的切向,造成管片环拼装误差过大,但随着管片环轴向慢慢纠正,拼装误差会慢慢减小。
管片环内外向不同初始偏位误差下,受初始偏位影响的后续50环管片的最大空间拼装误差变化规律如图12、图13所示。由图12、图13可得:管片的最大拼装误差与管片环初始外偏位误差值大致呈线性相关。由拟合曲线的斜率可以看出,管片环的内偏位误差对后续管片环拼装误差的影响更明显。为满足规范规定的拼装误差,管片环初始偏位内外偏移量的允许值分别为24.3 mm和48.8 mm。
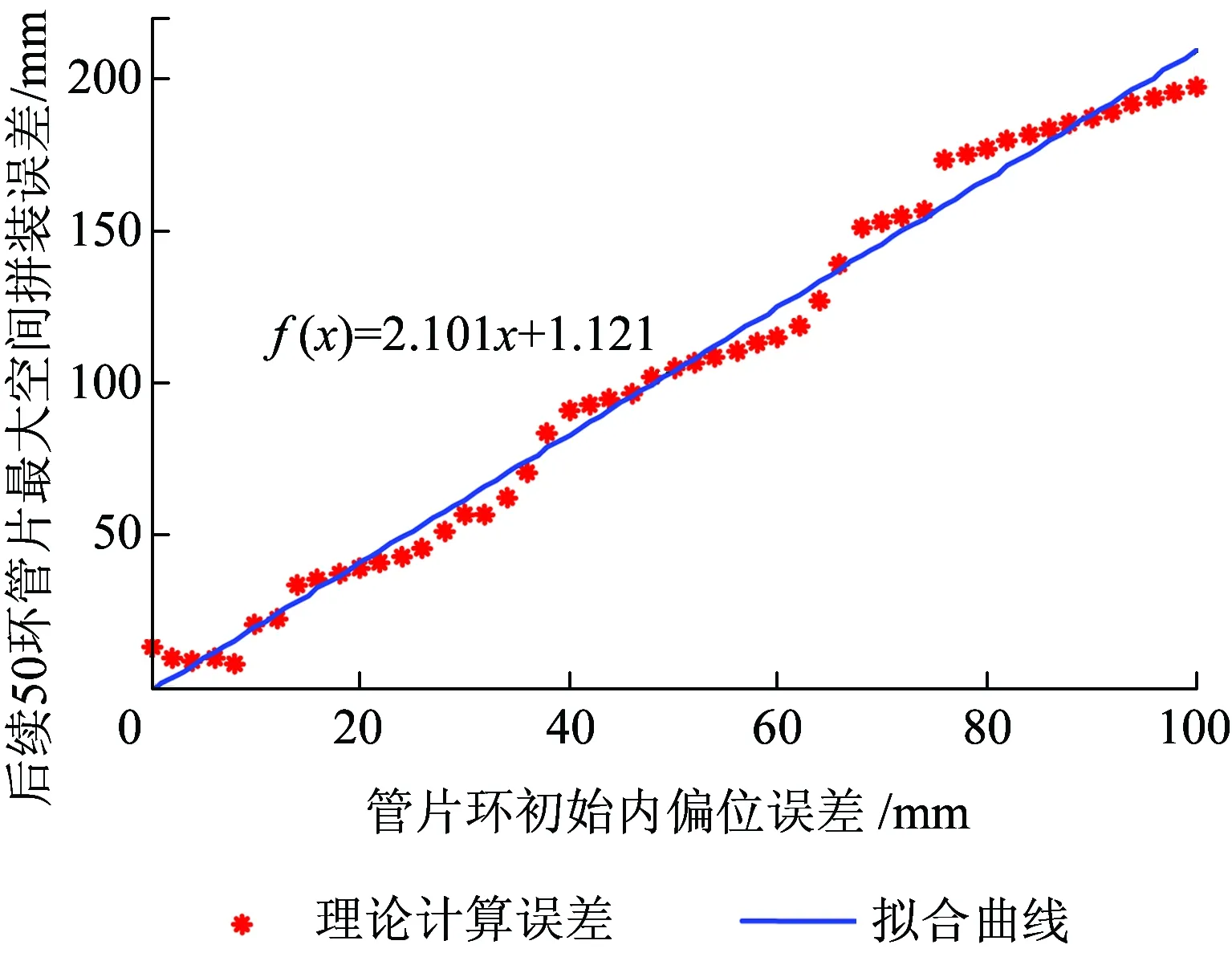
图12 管片环初始内偏位影响下后续50环管片的最大拼装误差
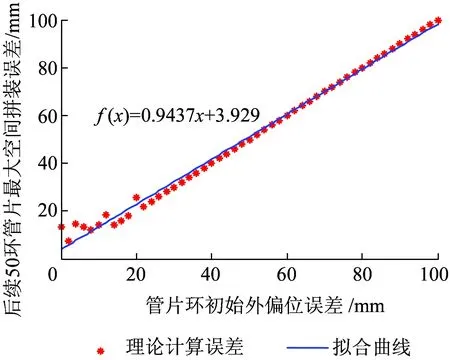
图13 管片环初始外偏位影响下后续50环管片的最大拼装误差
4.2 管片环偏向对后续曲线拟合的影响
管片环偏向是指管片环轴线偏离设计曲线上控制点的切向,规定轴线向外偏离设计曲线切向为正(以下简称外偏向),轴线向内偏离设计曲线切向为负(以下简称内偏向),如图14所示。通过计算发现:初始偏向对管片拟合曲线线形的影响较大,外偏向和内偏向对管片影响程度不同。

图14 管片环轴向偏向示意图
以管片环前进面中点作为确定曲线切向的控制点,分析管片环初始偏向对曲线拟合精度的影响,以及初始管片环偏向的允许范围。
不同管片环初始内偏向角度影响下后续50环管片最大空间拼装偏差如图15所示,可以看出:当轴线向内偏离时,即使偏离角度较小,如偏离0.5°,也可导致管片环的最大拼装误差达到74.8 mm;当管片轴线偏向大于0.6°时,在没有采用特殊措施时,按管片设计的排版方式将无法对曲线进行拟合。
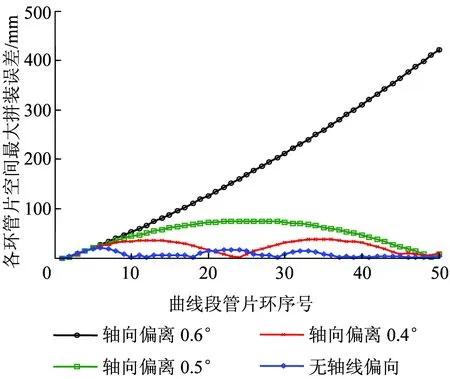
图15 管片环内偏向影响下曲线段各环管片的空间拼装误差
为确定管片环允许内偏向的范围,研究不同内偏向角度影响下后续50环管片的最大空间误差,如图16所示。从图16可以看出:管片环内偏向在不大于0.5°时,后续管片环的拼装误差较小;当管片内偏向大于0.5°时,管片环的拼装误差将剧烈增加,直至最后管片环无法对曲线进行拟合。同时,为满足规范规定的最大拼装误差(不大于50 mm),对应的管片环内偏向角度应不大于0.48°。

图16 管片环初始内偏向影响下后续50环管片的最大拼装误差
不同管片环初始外偏向角度影响下后续50环管片最大空间拼装偏差如图17所示。由图17可知:当管片轴线外偏1.5°时,管片的最大纠偏误差在95 mm左右,而当管片轴线外偏0.5°时,纠偏误差相对于管片轴线无初始偏位的情况无太大变化。比较图15和图17可以看出,相对于管片环内偏向的情况,管片环外偏向对后续管片的拼装误差影响较小。
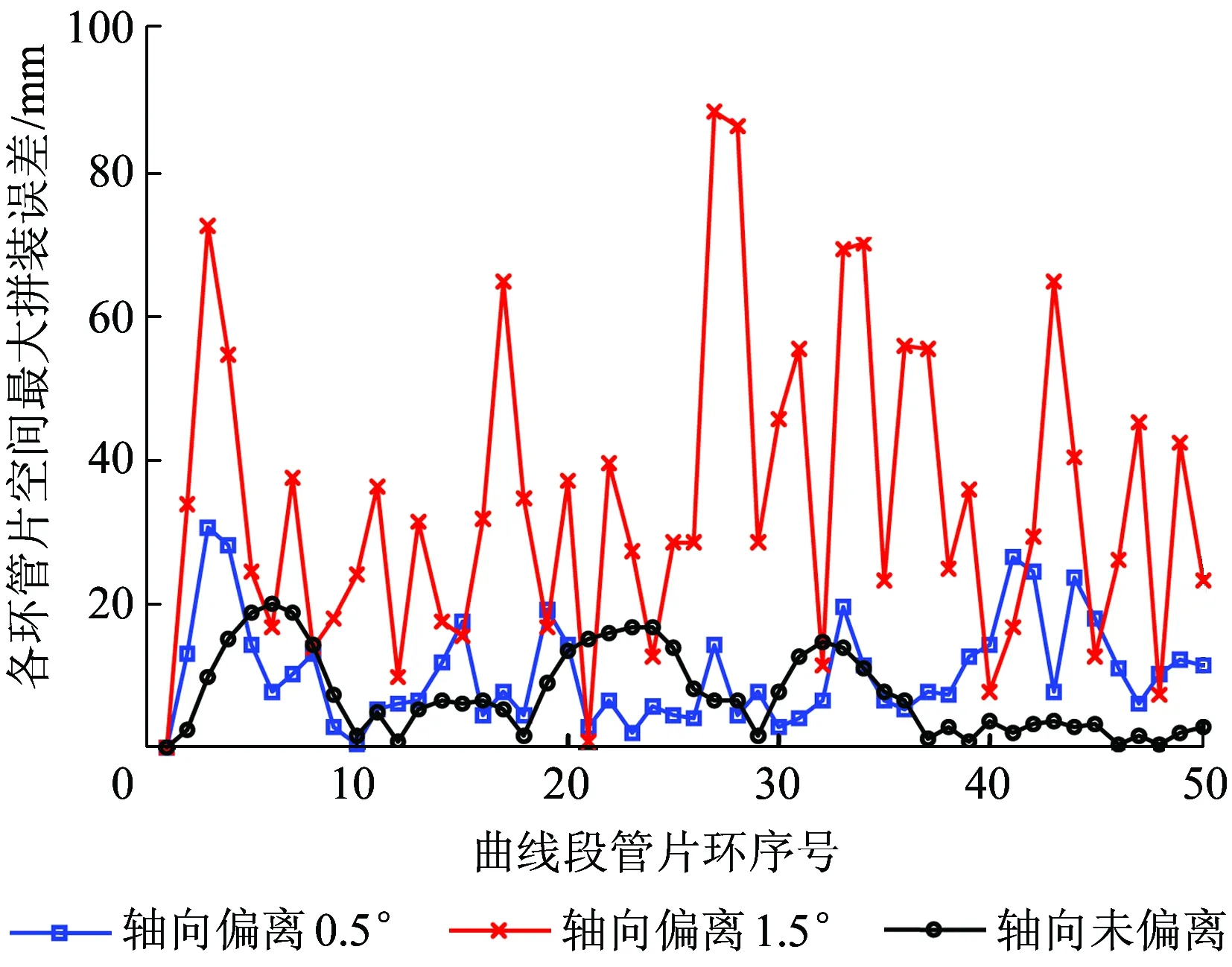
图17 管片环外偏向影响下曲线段各环管片的空间拼装误差
为确定管片环允许外偏向的范围,研究不同外偏向角度影响下后续50环管片的最大空间误差,如图18所示。由图18可得:为控制管片最大纠偏误差在规范规定值范围(不大于50 mm),管片外偏向角度不应大于0.93°。
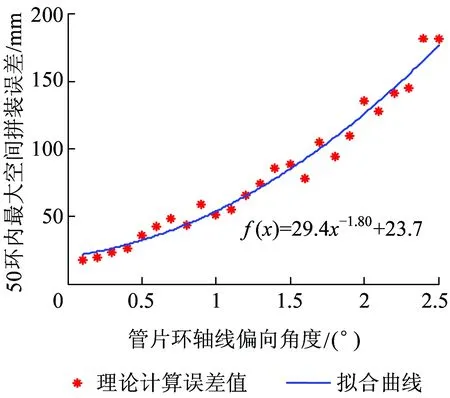
图18 初始外偏向影响下后续50环管片的最大拼装误差
5 结论
本文在通用楔形管片盾构隧道曲线拟合原理和关键算法基础上,对管片环能拟合最小曲线半径、管片环参数与曲线拟合精度的相关性、管片环初始拼装误差对曲线拟合精度的影响等关键问题进行研究。提出不同管片参数能拟合的最小曲线半径的判断标准,探讨最小曲线半径随管片参数变化的一般规律;同时,针对盾构隧道曲线拟合精度提出评价标准,结合工程实例探讨了管片参数对曲线拟合精度的影响;针对曲线纠偏问题,探讨管片环初始偏位和偏向对拟合工作的影响。得出结论如下:
(1)管片环能拟合的最小曲线半径随管片外径的增长线性增大,且该曲线斜率随管片幅宽的减小而减小;最小曲线半径随楔形量的增大而减小,楔形量的增大明显提高了管片环对小半径曲线的拟合能力,并且对于管片环质量、整体尺寸无大的影响。
(2)盾构隧道曲线段拟合精度随管片环幅宽减小、楔形量增大整体有提高趋势,该趋势只在一定范围内较明显,超过该范围减小管片幅宽或增大楔形量对于提高曲线拟合精度效果有限。过小的管片幅宽不仅增加盾构隧道渗漏环节,还会降低管片拼装效率。
(3)管片环初始偏位对管片环拟合曲线精度有一定影响。当管片环偏位位于曲线外侧时,管片拼装误差受影响的程度较小,当管片环偏位位于曲线内侧时,管片环的拼装误差将受到较大影响。对于典型参数下的地铁盾构隧道,通过计算发现,为满足规范规定的拼装误差,管片环初始偏位的内外偏移误差的允许值分别为24.3 mm和48.8 mm。
(4)管片环初始轴线偏向对管片的拼装误差影响明显,不同指向的初始管片环偏向对后续管片拼装误差影响各异。相比管片环外偏向,管片环内偏向将造成管片拼装误差明显增大,内偏角超过0.6°可能造成曲线无法拟合。同时,为满足规范规定的拼装误差,管片环内外偏向角度的允许值分别为0.48°和0.93°。
参考文献:
[1]何川,封坤.大型水下盾构隧道结构研究现状与展望[J].西南交通大学学报,2011,46(1):1-11.
HE Chuan,FENG Kun.Review and Prospect of Structure Research of Underwater Shield Tunnel with Large Cross-Section[J].Journal of Southwest Jiaotong University,2011,46(1):1-11.
[2]何川,张建刚,苏宗贤.大断面水下盾构隧道结构力学特性[M].北京:科学出版社,2010:1-3.
[3]周文波.盾构法隧道施工技术与应用[M].北京:中国建筑工业出版社,2004.
[4]戴仕敏,李章林,何国军.大型通用楔形管片拼装施工技术[J].隧道建设,2006,26(4):64-67.
DAI Shimin,LI Zhanglin,HE Guojun.Erection Construction Technology of Large-scale Universal Wedge-shaped Segments[J].Tunnel Construction,2006,26(4):64-67.
[5]何川,苏宗贤,曾东洋.地铁盾构隧道重叠下穿施工对上方已建隧道的影响[J].土木工程学报,2008,41(3):91-98.
HE Chuan,SU Zongxian,ZENG Dongyang.Influence of Metro Shield Tunneling on Existing Tunnel Directly Above[J].China Civil Engineering Journal,2008,41(3):91-98.
[6]杨群,谢立广.关于盾构隧道楔形管片环的思考[J].现代隧道技术,2010,47(3):56-59.
YANG Qun,XIE Liguang.Reflections on Wedge Segment Rings of Shield Tunnels[J].Modern Tunnelling Technology,2010,47(3):56-59.
[7]李围,何川.盾构隧道通用管片结构力学行为与控制拼装方式研究[J].铁道学报,2007,29(2):77-82.
LI Wei,HE Chuan.Study on Mechanical Behavior and Controlling Assembling Modes of Universal Segment Lining for Shield Tunnel[J].Journal of the China Railway Society,2007,29(2):77-82.
[8]刘凤华.盾构隧道通用管片拟合排版与管片选型技术研究[D].上海:同济大学,2007.
[9]宋瑞恒.盾构隧道通用管片排版与动态纠偏管理软件开发[D].上海:上海交通大学,2008.
[10]李伟平,郑国平.盾构隧道通用楔形管片排版系统的核心算法研究[J].现代隧道技术,2008,45(5):34-37,43.
LI Weiping,ZHENG Guoping.Study on Core Algorithm of Typesetting System for Universal Wedge Segments of Shield Tunnels[J].Modern Tunnelling Technology,2008,45(5):34-37,43.
[11]王腾飞,邓朝辉.盾构法隧道通用楔形环空间线路拟合技术的探讨[J].铁道勘察与设计,2004,134(2):41-45.
WANG Tengfei,DENG Chaohui.Discussion on the Technology of Curve Fitting of Shield Tunnel with Universal Wedge Segments[J].Railway Survey and Design,2004,134(2):41-45.
[12]常明,朱林.计算机图形学[M].2版.武汉:华中科技大学出版社,2001.
