基于ZAMD的高速铁路弓网接触压力及接触线不平顺时频分析

汪宏睿， 刘志刚， 宋 洋

(西南交通大学 电气工程学院， 四川 成都 610031)

电气化高速铁路中，电力机车运行时顶部受电弓与接触网之间的接触压力是表征其受流质量的重要指标[1〗。接触压力反应了受电弓和接触线之间的接触质量，接触压力过小会使弓网间产生电弧或电火花，甚至导致弓网离线；接触压力过大则会加剧受电弓弓头和接触线的磨损，表明接触网中存在硬点，可能导致刮弓事故的发生。不良的接触压力不仅会影响电力机车的受流质量，同时也会加剧弓网系统机械性能的损耗从而降低其使用寿命，严重时会造成弓网系统的损坏致机车停止运行。现行弓网接触压力评价指标主要应用于对弓网动态相互作用性能的评价，包括接触压力均值、标准差、最大值、最小值和离线率等，这些指标反映了接触压力在时域内的整体趋势和波动，但是无法反应其频域特性。

目前，国内外对于弓网间接触压力数据的频域分析多采用功率谱分析的手段。藤井保和等使用功率谱分析了日本新干线接触线的波状磨耗及其与弓网离线的关系[2〗；MitsuoAboshi等建立了日本新干线接触线不平顺功率谱，分析了接触线不平顺对接触压力的影响[3-4〗；Shunichi Kusumi等分析了接触压力信号功率谱的波形特征，提出根据接触压力功率谱的特征变化来诊断接触线状态；张卫华等在国内首先提出了接触线不平顺的概念[6〗；韩柱先等利用功率谱对刚性接触网的不平顺进行了数值模拟[7〗；宦荣华等讨论了实测高速铁路接触线垂向不平顺谱对接触压力的影响[8〗；刘志刚等提出了基于AR(Autoregressive)模型的接触网线谱，将接触压力功率谱用于弓网动态性能的评估。以上功率谱分析都基于被分析数据为平稳随机过程的假设，而表征弓网动态特性的接触压力数据波动成因复杂，接触压力并非是严格各态历经的，张晓晓使用多种检验方法对接触压力数据平稳性进行了分析，认为采样里程在500 m以下的接触压力数据呈现出非平稳性[11〗，尤其是在实际线路结构中定位器、锚段关节和线岔及可能存在的接触线硬点以不均匀的间距出现，对应的接触压力数据将呈现明显的非平稳性。因此，使用非平稳信号处理的方法对接触压力进行分析，不仅更符合接触压力短里程数据本身的非平稳性，还能从时间-频率(里程-空间频率)二维角度得到更精确的信号特征描述，有利于接触压力时频域特征的提取，观测接触压力频率成分的数值及其持续里程，明确接触压力数据中不同频率成分物理意义及其存在的空间位置。同时，接触线表面磨耗导致不平顺的检测技术要求测量精度很高，导致测量难度大且成本高，而接触压力是间接反映接触线不平顺的测量量之一，通过时频分析可辨识由于接触网不平顺等因素造成的接触压力中异常波长成分的存在，以便在接触压力时域或单一频域指标出现异常前确定接触线不平顺的存在。

本文以高速铁路的弓网接触压力仿真数据为基础，讨论适用于其非平稳特性的时频分析方法，使用ZAMD(Zhao-Atlas-Mark Distribution)[12〗对接触压力进行时频分析。以此为基础，在弓网有限元模型中模拟接触线的全局、局部不平顺和复合不平顺，使用ZAMD分析接触线不平顺下的接触压力时频特性，诊断并定位接触线不平顺的空间位置，为通过接触压力数据评估接触线不平顺状态提供一种思路。

1 接触压力时频域分析

非平稳信号的时频分析分为线性变换和非线性变换两大类[13〗。线性变换主要包括短时Fourier变换、Gabor变换和小波变换等，其中短时Fourier变换和Gabor变换的时频分辨率较差，小波变换不适用于包含多种相近频率成分信号的分解且对小波基的选取要求很高。非线性变换使用时间和频率的联合函数描述信号的能量密度随时间(里程)变化，主要指是Cohen类时频分布[14〗，信号z(t)的Cohen类分布定义为

( 1 )

式中：t、ω分别为信号瞬时时间和瞬时频率；Rz(t,τ)为信号的时变自相关函数

( 2 )

式中：φ(τ,v)为Cohen类时频分布的核函数；“*”表示取复共轭；u、τ和v分别为积分计算的时间位置、时间位移和频率位移变量。在核函数φ(τ,v)=1的特殊情况下，Cohen类分布就是Wigner-Ville分布

( 3 )

Wigner-Ville分布具有最好的时频聚集性，但其存在严重的交叉项现象和无物理意义的负频率，在应用中需要对其进行改进，即在不影响其时频聚集性情况下最大限度地抑制交叉项。围绕交叉项的抑制和Wigner-Ville分布的改进，已提出伪Wigner分布、平滑伪Wigner分布、Butterworth分布、Choi-Williams分布、Born-Jordan分布和Zhao-Atlas-Mark分布[12〗等Cohen类分布，各分布的核函数见表1，表中η(τ)、g(τ)均为时间窗函数,G(v) 为频率窗函数,α、M和N均为调节相应核函数取值的参数。

不同Cohen类分布适用于分析具有一定时频特性的信号，目前还没有一种分布能对所有信号取得较好的时频分析效果。电气化铁路弓网接触压力信号中包含复杂的频率成分，具有频率成分数量多且低频部分能量集中的特点，需要选取适当的时频分析方法对其进行分析。在使用Cohen类时频分布时，将实数信号转换为解析信号，能直接消除结果中的负频率成分和正负频率之间的交叉项[15〗，通过Hilbert变换即可实现解析信号的转换

z(t)=s(t)+j·H[s(t)]

( 4 )

式中：s(t)表示待分析实数信号；H[·]表示Hilbert变换[16〗；z(t)为解析信号。

表1 典型的Cohen类时频分布核函数

本文所使用的接触压力数据均来自京津高铁仿真模型[17〗，分别使用了DSA380和SS400+两种型号受电弓的三质量块模型，其不同速度下接触压力时域统计量见表2，由表2可见各组数据符合基本规律，整体趋势上看SS400+受电弓的接触压力均值较小，而DSA380受电弓的接触压力标准差较小。

表2 仿真接触压力时域统计量

取共10跨接触压力数据的中间8跨稳定数据作时频分析，数据长度为384 m(跨距为48 m)，空间采样频率为0.5 m，符合数据总长度小于500 m的非平稳性分析要求。使用几种典型Cohen类分布对300 km/h时速、DSA380受电弓下接触压力的时频分析，结果见图1。图1(a)～图1(f)均为等高线图，图中横坐标表示里程，纵坐标表示空间频率，颜色由蓝到红表示能量密度由小到大(见图中能量条带所示)，白色表示该处无能量。在接触压力信号的时频分析结果中，若某纵坐标空间频率处所对应的等高线图中存在能量表征，则称该接触压力信号中存在该空间频率成分，空间频率的倒数即是该接触压力信号中存在的空间波长成分。

由图1可观察到WVD、CWD、BJD和BUD对接触压力的时频分析效果很差，存在交叉项的情况十分严重，而从SPWD和ZAMD的结果中可以较清晰观察到数条完整的水平线，表示在被分析数据段内存在该空间频率成分。其中，接触压力在空间频率0.021 m-1处能量密度最大，该处正好表征了以接触网跨距为周期的波长成分47.6 m，与模型跨距48 m相符，是正常接触压力中能量最集中的波长成分，与文献[18〗的分析结果是一致的。考虑到使用SPWD时需要设定时域和频域平滑窗口的宽度，且图1(b)中低频部分交叉项情况严重，无法精确分辨水平线对应的空间频率，故本文选择使用ZAMD进行接触压力的时频分析。为简化图形表示，以下时频分析结果的等高线图中省略了表示能量大小的能量条带图。

图2为不同车速下的接触压力信号时频分析结果，可以观察到4种高速车速下，共有9个空间频率处的水平线存在，其中高频部分2条水平线对应空间频率为0.760 m-1和0.737 m-1，即波长1.32 m和1.36 m处，低频部分7处空间频率对应波长为3.21 、4.85、8.01、9.51、11.9、23.8m和47.6 m，其中47.6 、23.1、9.51 m和4.85 m分别表征了跨距、半跨距、9.5 m吊弦间距和5 m吊弦间距(波长位置见图1(f)中红色箭头)，其他波长成分存在且不随车速改变而改变，因此可认为是由弓网相互作用引起振动产生的。同时，可观察到随着车速的改变，接触压力中的部分波长成分随之变化，图中红色椭圆框内为接触压力中变化的波长成分，可见总体上变化的波长成分随速度的增大而增多且波长增大，速度为350 km/h时波长成分最复杂。

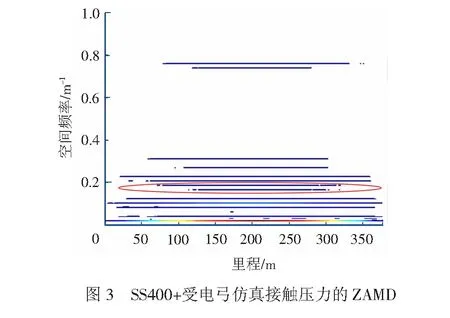
图3为SS400+受电弓在时速300 km/h下的接触压力时频分析结果，对比图2(c)可观察到，SS400+受电弓包含了DSA380中的所有波长成分，同时多出了图3红色椭圆框内2处波长，说明不同的弓网匹配造成不同的弓网接触压力波长成分，其中接触网结构不改变则部分成分保持不变。同时，一定程度上说明表2中SS400+受电弓的接触压力标准差相较于DSA380更大，是由于弓网交互中所产生的的振动频率增多造成的。

2 接触线不平顺模拟

柔性接触网中的接触线不平顺是由接触线本身位置、形状和接触线表面磨耗共同决定的[9〗，目前研究多集中于接触线垂向不平顺方面，一般使用接触线导高数据建立接触线垂向不平顺谱，以评估接触线不平顺状态[19〗。鲜有学者提出可用于模拟接触线垂向不平顺的拟合功率谱，为验证本文采用的ZAMD时频分布具备有效分析接触压力中不平顺波长的能力，本文在接触网的有限元模型中，引入文献[6〗中所提出的理想状态下接触线表面不平顺余弦波形公式

( 5 )

式中：A表示不平顺幅值；λ表示不平顺波长；x表示沿接触线方向坐标。该余弦波形能有效模拟接触线波状不平顺，同时有利于本文对ZAMD分析结果的验证。模拟接触线不平顺即是在接触线正常导高的基础上，加入上式计算值。改变并组合上式中不平顺幅值和波长，即可模拟接触线全局不平顺、局部不平顺和复合不平顺状态，各种不平顺示意图见表3。

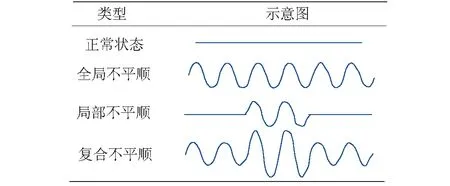
表3 3种接触线不平顺示意图

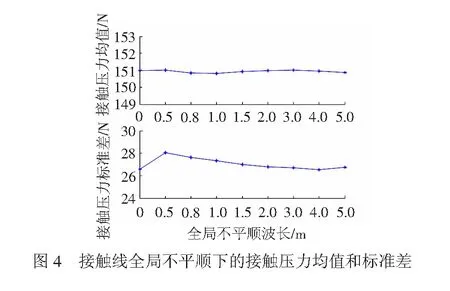
根据以往研究经验及实测数据[4,6,8〗的不平顺数值大小，本文取不平顺幅值A=1 mm，观测ZAMD是否能够分析小幅值的不平顺成分。由于接触线不平顺波长一般小于吊弦间距，因此取不平顺波长λ为0.5～5 m，分别仿真受电弓以300 km/h通过十跨接触网的接触压力。仿真结果表明，在不平顺幅值1 mm时弓网间未出现离线现象，接触压力最小值、最大值分别为56.1 N、245.7 N，其均值及标准差见图4。可观察到幅值为1 mm的接触线全局不平顺并未对接触压力均值造成较大影响，其值稳定在151 N左右；接触压力标准差则在26.7 N左右呈现出一定的变化趋势，当接触线不平顺波长较短即对应频率较高时，引起弓网间的高频振动使接触压力标准差略有增大。因此可以说，通过接触压力的时域指标无法直接观测到接触线不平顺。

3 基于ZAMD的接触线不平顺分析

在使用ZAMD对接触线不平顺状态下的接触压力进行时频分析时，期望能够观察到对应接触线不平顺波长的存在。对于接触线局部不平顺下的接触压力，则期望能观察到相应波长及波长对应空间位置，同时实现不平顺波长的诊断和定位功能。

3.1 接触线全局不平顺波长分析

利用前文仿真数据，对存在幅值1 mm、波长0.5～5 m的接触线全局不平顺的接触压力进行时频分析，图5为接触线不平顺波长为0.5 、1 、2 m和3 m时的分析结果。

由图5可以看出，除包含图1(f)中的所有正常波长成分以外，图5(a)～5(d)分别在波长0.5、1、2 m和3 m的位置出现了表征接触线不平顺波长的水平线，表明使用ZAMD能有效分析并观察到接触压力中存在的接触线不平顺波长成分。同时，随着波长的增大，对应接触线不平顺波长的持续里程(即水平线长度)缩短，这是由于接触压力中低频部分能量大，越靠近低频部分的接触线不平顺能量越容易被覆盖，导致表征不平顺波长的波形旁瓣被淹没，造成水平线两端的缩短。

总体来说，使用ZAMD能较有效的观测到弓网接触压力中的接触线全局不平顺波长成分，且不平顺波长越短效果越佳。

3.2 接触线局部不平顺波长分析

由于接触线局部不平顺持续里程短，其能量相对于全局不平顺很小，使用频率-能量表示的传统功率谱估计方法一般无法观测到相应的接触线不平顺波长，而使用时频域分析的方法则能较好地表征出持续里程较短的波长成分。

根据式( 5 )，在模拟接触线局部不平顺时限定x∈[a,b〗，a和b分别表示局部不平顺的起始位置。本文分别仿真了接触线在第四跨中存在波长2 m不平顺和第六跨中存在波长2.5 m不平顺时的接触压力，图6(a)和图6 (b)为2种情况下接触压力ZAMD的时频分析。

图6(a)可在里程区间[107 m,139 m〗内观测到2 m的波长成分，由于接触压力取的是接触网十跨的中间八跨数据，因此理想情况下该成分在图中应出现的里程区间为[96 m,144 m〗，持续里程的两端变短同样是由于波形旁瓣被淹没造成的；同理在图6(b)中，理想情况下存在2.5 m波长成分的里程区间为[192 m,240 m〗，实际分析结果为[205 m,235 m〗。可以说，ZAMD对弓网接触压力中的接触线不平顺波长成分有一定的定位功能，其误差在于ZAMD分析出的里程范围比实际不平顺范围小，其在起始端分别缩短了数米不等。尽管如此，ZAMD分析结果对于接触线局部不平顺的定位仍具有很高的参考价值。

3.3 接触线复合不平顺波长分析

接触线的复合不平顺考虑为多种全局不平顺和局部不平顺的叠加，复合的全局不平顺可使用下式模拟

( 6 )

式中：λk(k=1,2,…,N)表示N个全局不平顺波长；x∈[-∞,∞〗。对存在不平顺幅值1 mm，包含波长1 m和1.5 m的复合全局不平顺接触线进行仿真，其接触压力ZAMD的时频分析见图7。由图7可清晰观察到表征2个全局波长成分的水平线，说明接触压力可直接反应出接触线中的复合全局不平顺，且使用ZAMD可有效分析出多个波长成分。

由全局和局部不平顺同时组成的复合不平顺更接近实际的接触线不平顺状态，参考式( 6 )，其模拟式为

y(x,x1,x2,…,xM)=

( 7 )

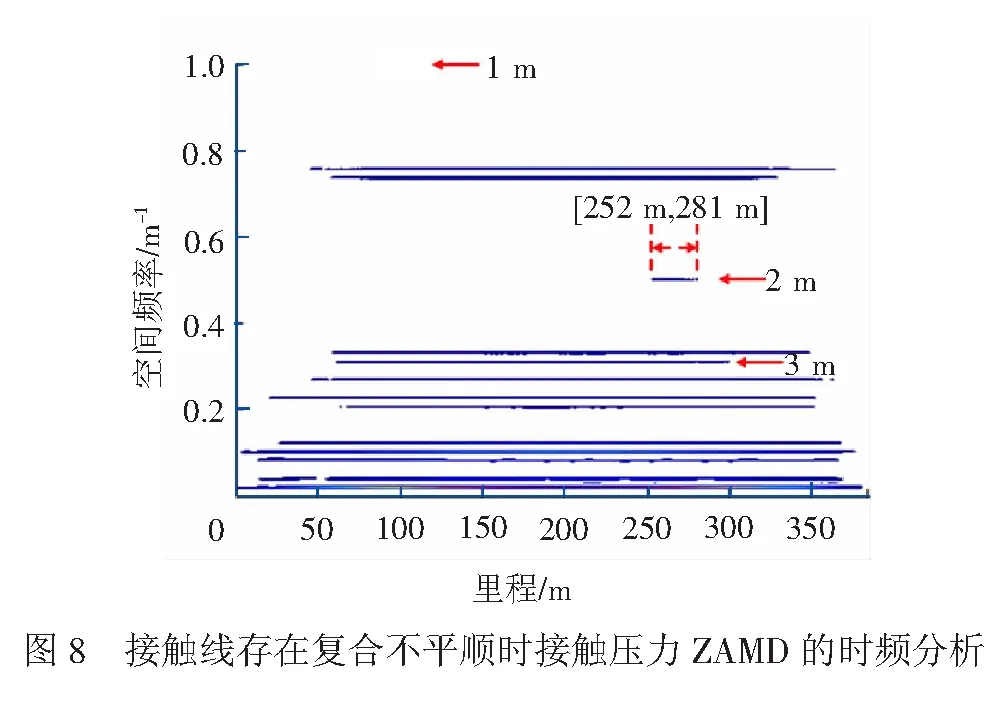
由于实际线路的接触线不平顺，特别是既有线路的接触线不平顺随着时间发展越来越复杂，若要通过接触压力时频分析结果中的波长成分判断接触线不平顺的存在或者恶化，则至少需要满足以下条件之一：

(1) 在接触网设计阶段，通过仿真手段明确理想条件下的接触压力时频特性，以作为观测接触线不平顺波长的参照；

(2) 在弓网动态验收阶段，明确验收时的弓网接触压力时频特性，以便通过运营后测量的接触压力数据时频特性的变化判断接触线不平顺的存在及严重程度；

(3) 对于既有线路，通过当前接触压力时频特性与较早接触压力时频特性的对比，以确定接触线不平顺的存在及严重程度。

4 结论

应用于非平稳信号的时频分析理论已经历了数十年的发展历程，其时间-频率(里程-空间频率)形式的二维分析方法为确定信号中某频率的存在时间提供了可能。本文通过试验确定了适用于分析高铁弓网接触压力信号的时频分布——ZAMD，在弓网有限元模型中使用余弦波形模拟接触线全局、局部和复合不平顺，采用该时频分布对正常和存在接触线不平顺的接触压力进行了时频分析。

分析结果表明，使用ZAMD不仅能有效分析正常接触压力中的波长成分，还能较有效地表征出接触压力中体现出的接触线不平顺波长，并且对接触线的局部不平顺波长成分有一定的定位能力，同时接触线不平顺波长越短则分析效果越佳。本文方法为通过弓网接触压力评估接触线的复杂不平顺状态提供了一种思路，其定位接触线局部不平顺的功能对于接触网养护工作亦有一定参考价值。

参考文献：

[1]于万聚. 高速电气化铁路接触网[M〗.成都:西南交通大学出版社,2003.

[2]藤井保和，易厚梅. 新干线受流系统高速化的技术研究[J〗. 电力牵引快报, 1995(10):20-25.

TAMOTSU Fuji, YI Hou-mei. Technical Research of the ShinkansenLine Current Collection System[J〗.Electric Traction,1995(10): 20-25.

[3]ABOSHI M,MANABE K.Analyses of Contact Force Fluctuation Between Catenary and Pantograph[J〗. Railway Technical Research Institute,2000, 41(4):182-187.

[4]ABOSHI M.Precise Measurement and Estimation Method for Overhead Contact Line Unevenness[J〗. IEEJ Transactions on Industry Applications, 2004,124(9):871-877.

[5]KUSUMI S, FUKUTANI T, NEZU K. Diagnosis of Overhead Contact Line Based on Contact Force[J〗. Quarterly Report of RTRI, 2006, 47(1): 39-45.

[6]张卫华, 梅桂明, 陈良麒. 接触线弛度及表面不平顺对接触受流的影响分析[J〗.铁道学报, 2000, 22(6): 50-54.

ZHANG Weihua, MEI Guiming, CHEN Liangqi. Analysis of the Influence of Catenary’s Sag and Irregularity Upon the Quality of Current-feeding[J〗. Journal of the China Railway Society, 2000, 22(6): 50-54.

[7]韩柱先, 王国梁.刚性接触网的不平顺分析[J〗.铁道工程学报, 2007, 103(4):61-64.

HAN Zhuxian, WANG Guoliang. Unevenness Analysis of Overhead Rigid Suspension Catenary[J〗.Journal of Railway Engineering Society,2007,103(4):61-64.

[8]宦荣华, 焦京海, 苏光辉, 等. 计及接触线垂向不平顺的弓网耦合动力学分析[J〗.铁道学报, 2012, 34(7):15-21.

HUAN Ronghua, JIAO Jinghai, SU Guanghui, et al. Dynamics of Pantograph-catenary Coupled System Considering Contact Wire Vertical Irregularity[J〗. Journal of the China Railway Society, 2012, 34(7): 15-21.

[9]刘志刚,韩志伟. 基于AR模型的电气化铁路接触网线谱研究[J〗. 铁道学报, 2013,35(12):24-29.

LIU Zhigang, HAN Zhiwei. Study on Electrical Railway Catenary Line Spectrum Based on AR Model[J〗. Journal of the China Railway Society, 2013,35(12): 24-29.

[10]汪宏睿, 刘志刚, 韩志伟, 等. 电气化铁路弓网接触压力功率谱的特征提取[J〗. 铁道学报, 2014, 36(11): 23-28.

WANG Hongrui, LIU Zhigang, HAN Zhiwei, et al.Feature Extraction of the Pantograph-catenary Contact Force Power Spectrum of Electrified Railway[J〗. Journal of the China Railway Society, 2014, 36(11): 23-28.

[11]张晓晓.基于信号处理的电气化铁路弓网接触压力分析[D〗. 成都：西南交通大学, 2013.

[12]ZHAO Y, ATLAS L E, MARKS R J. The Use of Cone-shaped Kernels for Generalized Time-frequency Representations of Nonstationary Signals[J〗. Acoustics, Speech and Signal Processing, IEEE Transactions on, 1990, 38(7): 1084-1091.

[13]张贤达.现代信号处理[M〗. 北京:清华大学出版社, 2002.

[14]COHEN L. Time-frequency Analysis[M〗.Englewood Cliffs, NJ: Prentice hall, 1995.

[15]JONES D L, Parks T W. A Resolution Comparison of Several Time-frequency Representations[J〗. Signal Processing, IEEE Transactions on, 1992, 40(2): 413-420.

[16]BOASHASH B.Note on the use of the Wigner Distribution for Time-frequency Signal Analysis[J〗.Acoustics, Speech and Signal Processing, IEEE Transactions on,1988,36(9):1518-1521.

[17]刘志刚, 侯运昌, 韩志伟, 等. 基于风场模拟的高铁接触网动态性能分析[J〗. 铁道学报, 2013, 35(11): 21-28.

LIU Zhigang, HOU Yunchang, HAN Zhiwei, et al. Analysis onDynamic Characteristics of High-speed Railway Catenary Based on Wind Filed Simulation[J〗. Journal of the China Railway Society, 2013, 35(11): 21-28.

[18]KIM J. An Experimental Study of the Dynamic Characteristics of the Catenary-pantograph Interface in Highspeed Trains[J〗. Journal of Mechanical Science and Technology，2007, 21(12): 2 108-2 116.

[19]宦荣华, 宋亚轻, 朱位秋. 基于相干分析的接触导线高度不平顺不利波长研究[J〗. 浙江大学学报(工学版), 2013, 47(9):1 599-1 602.

HUAN Ronghua, SONG Yaqing, ZHU Weiqiu. Study ofDetrimental Wavelengths of Contact Wire Height Irregularity Based on Coherence Analysis[J〗. Journal of Zhejiang University:Engineering Science,2013,47(9):1 599-1 602.